GNSS三天線遠海船舶姿態測量方法

衛進進，辛明真，石 波，劉 會，陽凡林

GNSS三天線遠海船舶姿態測量方法

衛進進1，辛明真1，石 波1，劉 會1，陽凡林1,2

（1. 山東科技大學 測繪科學與工程學院，山東 青島 266590；2. 自然資源部海洋測繪重點實驗室，山東 青島 266590）

針對海洋導航測姿中，遠海無法采用岸邊架設基準站的形式，導致全球衛星導航系統（GNSS）實時動態差分（RTK）高精度相對定位模式并不適用的問題，提出1種GNSS遠海測姿方法：以GNSS三天線為基礎，通過直接解法計算船體姿態信息，不需要提前測定基線長度，可直接對觀測值求解，模型簡單、計算量小；并采用動態參考站差分（MBD）與精密單點定位（PPP）進行GNSS 三天線姿態計算；最后設計遠海測姿實驗，分別采用MBD、PPP，與Seapath 320高精度導航測姿系統進行對比分析。結果表明，MBD模式下的測姿精度明顯優于PPP模式，且測姿精度穩定，是提高遠海姿態觀測可靠性的有效方法。

全球衛星導航系統；姿態測量；動態參考站差分；精密單點定位；定位誤差；測姿精度

0 引言

常見的海洋測量中，如海洋重力測量、船載激光測量、海洋磁力測量、多波束水深測量等，都需要進行姿態改正。船舶姿態測量是指獲取和解算船體運動過程中的姿態信息，包括航向角、俯仰角、橫滾角等船姿參數。目前，大部分海洋導航測姿系統都是利用高精度慣性傳感器進行姿態測量的，其原理是將慣性空間力學定律作為基本依據，使用加速度計、陀螺儀等慣性器件測量船體運動的加速度，最后通過積分運算得到船體的姿態參數[1]。但慣性器件存在導航誤差隨時間累積的問題，而且慣性導航測姿系統結構復雜、成本較高。隨著全球衛星導航系統（global navigation satellite system, GNSS）導航定位技術的不斷發展，GNSS姿態測量技術以其不受時間地點的限制、沒有誤差累積缺陷、精度穩定、可靠性強且成本較低等優勢，近年來已經成為國內外關注的熱點，可為基于慣性傳感器的海上姿態測量提供必要的補充。

GNSS設計初衷是為確定空間點位信息，但很早就有學者提出借助GNSS進行姿態測量[2]，然而局限于早期的技術成熟度和硬件發展水平，對GNSS測姿的探索多局限于仿真研究[3-4]。隨著GNSS技術的不斷發展，其定位精度也越來越高，使得GNSS高精度測姿成為可能。1986年，文獻[5]首次利用全球定位系統（global positionging system, GPS）載波相位觀測值，解算得到平臺的姿態；美國天寶（Trimble ）和阿什泰克（Ashtech）公司分別推出TANS Vector姿態/位置測定系統和3DF姿態/航向測定系統[6]；清華大學于1999年開展GPS載體姿態測量，主要應用于航天姿態測量[7-8]。隨后，各類測姿算法不斷優化提高，文獻[9]提出了最小二乘模糊度搜索算法，文獻[10-12]提出四元數測姿解算法并對其進行不斷優化，文獻[13]提出基于自適應卡爾曼濾波的GNSS測姿方法等。GNSS測姿也被廣泛應用到實際生產和海洋測繪研究中，文獻[14]分析了測船在非勻速直線運動狀態下GNSS測姿與慣性測姿的精度；文獻[15]構建了GNSS定位誤差、測姿誤差與水深測量誤差之間的關系方程；文獻[16]對GNSS/SINS組合測姿進行了分析驗證（其中SINS為捷聯慣導系統（strapdown inertial navigation system）的縮寫）。盡管GNSS姿態測量的理論方法日趨成熟，但目前的研究多局限在陸地及近海的相關測量，對于無法架設基準站的遠海及一些特殊區域，如何開展高精度的GNSS測姿仍具有較高的研究價值。

遠海GNSS標準單點定位（standard single point positioning，SPP）測量精度為米級，顯然，難以滿足GNSS高精度測姿的要求；基于靜態參考站的相對定位技術，如實時動態差分（real time kinematic，RTK）、后處理動態差分（post processed kinematic，PPK），通過對基準站與流動站的載波相位觀測值進行差分，減弱了各類誤差的影響，可以獲得厘米級甚至毫米級的定位精度，但其顯然并不適用于遠海。因此，針對遠海GNSS測姿問題，本文主要對基于動態參考站差分（moving-baseline model, MBD）、PPP的GNSS測姿精度進行驗證分析，為遠海GNSS測姿工程項目與研究分析提供參考。

1 三天線GNSS姿態測量

姿態是指船體坐標系（vessel body frame system, VFS）與當地水平坐標系（local level system，LLS）的對應關系[15]，在實際應用中，以橫搖角（roll）、縱搖角（pitch）、及航偏角（yaw）來表示姿態信息[17]，如圖1所示。

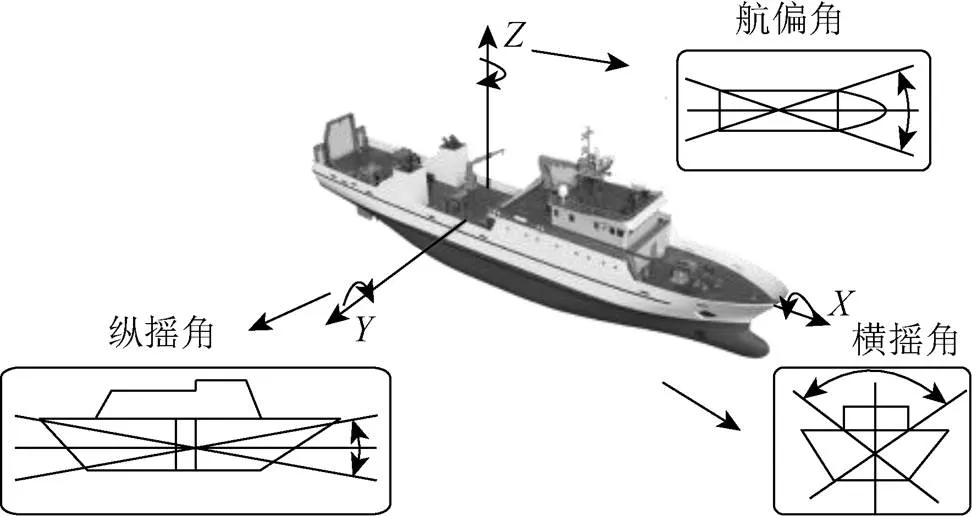
圖1 姿態角示意圖

航向角為船縱軸方向的方位角，橫搖角為在船體坐標系平面內，船體橫軸與軸的夾角，左向上為正，縱搖角為在船體坐標系平面內，船體縱軸與軸的夾角，向上為正。船體的姿態角由船舶上固定位置的GNSS接收機天線在同一歷元的觀測信息推算而得。隨著GNSS應用于測姿研究的不斷深入，出現了如平面布局法、四元數測姿算法、直接法等算法。由于平面布局法、四元數法等取決于初始姿態角和特殊的天線布局，因此，本文主要介紹解算姿態角的直接算法，此方法不需要提前測定基線長度，可直接對觀測值求解，模型簡單、計算量小。

本文以GNSS 三天線為基礎，通過直接解法計算船體姿態信息，因GNSS測量信息為1984世界大地坐標系（world geodetic coordinate system 1984, WGS84）下的坐標，想要得到較為精準的姿態信息，就需要建立WGS84坐標系與當地水平坐標系及船體坐標系之間的相互轉換關系，以布爾莎模型為理論基礎求解各個坐標系之間的轉換參數。

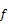
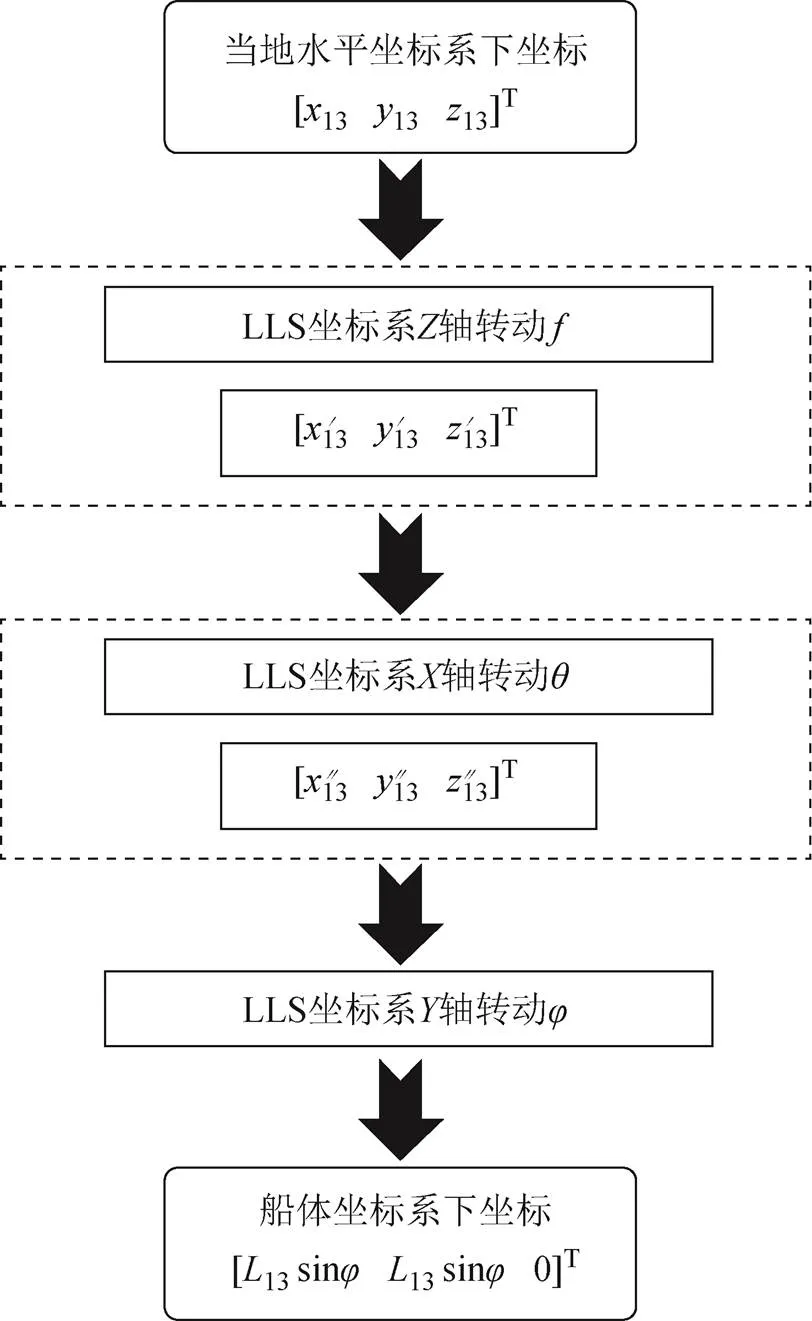
圖2 姿態參數與坐標系關系

姿態角參數的計算公式為：

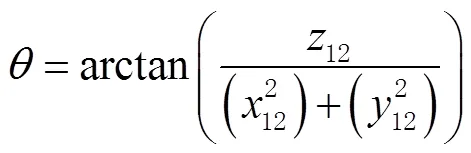
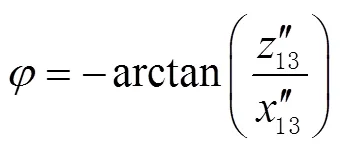
其中

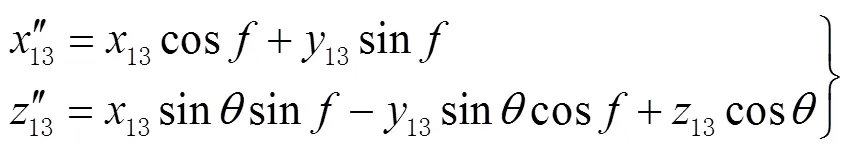
2 GNSS遠海定位方法

利用GNSS偽距進行導航和標準單點定位的精度約為數米，相對定位是主要的精密定位技術。相對定位使用高精度的載波相位觀測值，需要在一定區域范圍內有同步觀測的多臺接收機，通過消除未知點和參考點之間與空間相關的觀測誤差，可獲取厘米級甚至毫米級精度的定位結果，但遠海定位存在的主要問題是無法架設參考站，因此主要的定位方法有PPP、MBD。

1）精密單點定位（PPP）。PPP是使用單臺GNSS接收機的相位觀測值以及精密衛星軌道和鐘差產品，來改正GNSS 信號傳播過程中的各項誤差，獲取測站的高精度坐標值的1種定位方法。精密單點定位偽距和載波單點定位的觀測方程為

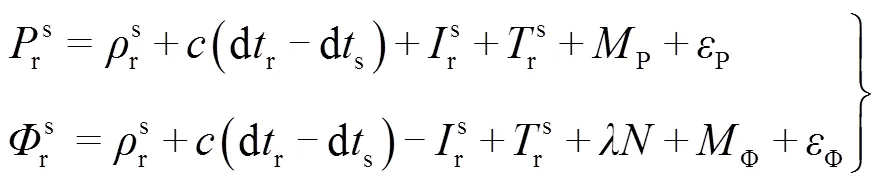
PPP無需建立控制網或參考站，單臺接收機即可作業，成本低，不受測站間基線長度的限制，理論上可在全球任何地區獲取框架一致的相同定位精度。PPP的缺點是收斂時間較長，這限制了PPP 高精度定位在實際工作中的使用。

2）動態參考站差分（MBD）。MBD也稱動對動定位，如果流動站和基準站接收機都在移動，并且流動站相對于基站的相對位置是唯一確定的，則可以使用MBD獲得較為準確的相對位置關系。

當接收機1、接收機2接收機同步觀測衛星、時，有單差觀測方程組

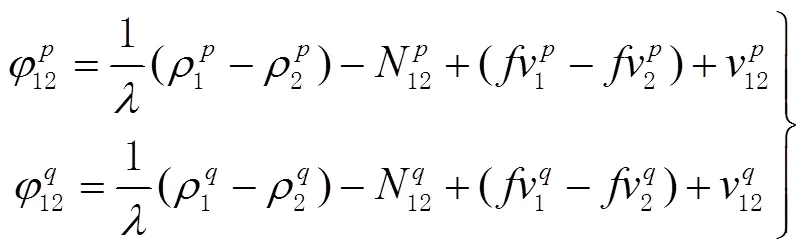
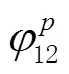
對式（6）中的2式間求差得

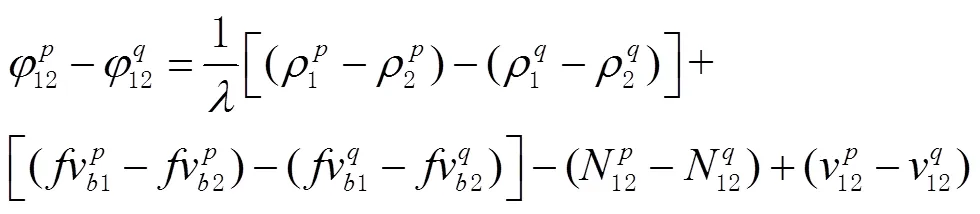
經整理得雙差載波相位觀測方程為

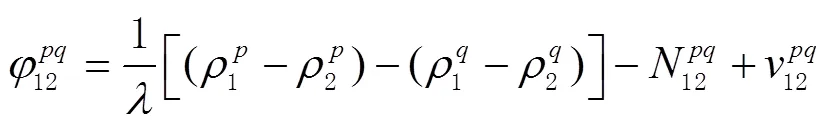
在動態參考站差分模式下，基準站位置不固定，可以通過逐點的單點定位來估計的。一旦獲得基準站位置，就通過短基線解算模型來估計流動站的位置，這種解算模式下，只對相對位置才有意義。其較為理想的相對位置關系，對于姿態解算具有較好的研究意義。

3 實驗與結果分析

為驗證MBD解算模式下GNSS姿態測量的精度，進行了3天線GNSS船載測姿實驗。本次實驗一共采用3臺南方GNSS接收機進行數據采集工作，天線布設方面采用如圖3所示布設方式。以Seapath 320高精度姿態儀的測量值作為參考數據。若以均方根（root mean square, RMS）值來表示測量精度，則Seapath 320的橫搖角及縱搖角的RMS值均為0.02°，航向角的RMS值為0.065°，這樣的高精度完全可以認為Seapath 320的測量結果為真值。

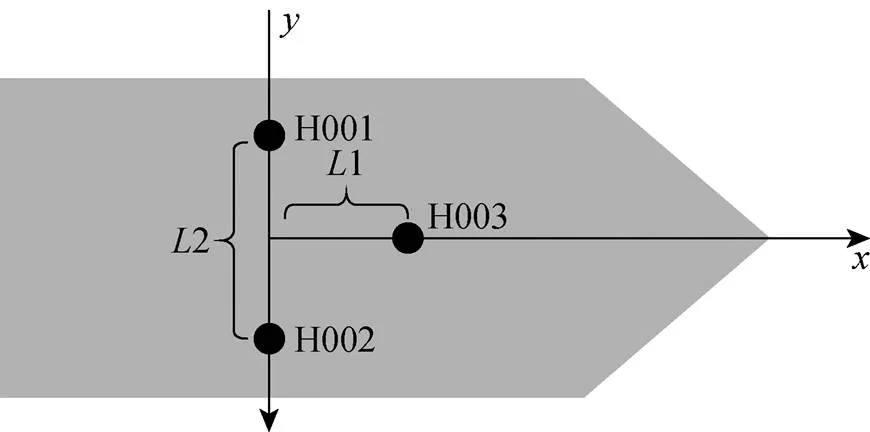
圖3 GNSS 三天線安裝示意圖

本文以RTKLIB為處理平臺，通過使用精密星歷及合理的經驗模型，盡可能提高GNSS解算精度，PPP解算精度如圖4所示，MBD解算精度如圖5所示。將GNSS多天線計算的姿態角與Seapath 320測姿數據進行比對，圖6為縱搖角、橫搖角、航向角對比圖，其中ATT（attitude）表示Seapath 320系統測量的船體姿態信息。圖7為PPP、MBD解算姿態數據與Seapath 320系統測姿數據較差圖。表1統計了不同GNSS解算方法計算姿態的標準差。

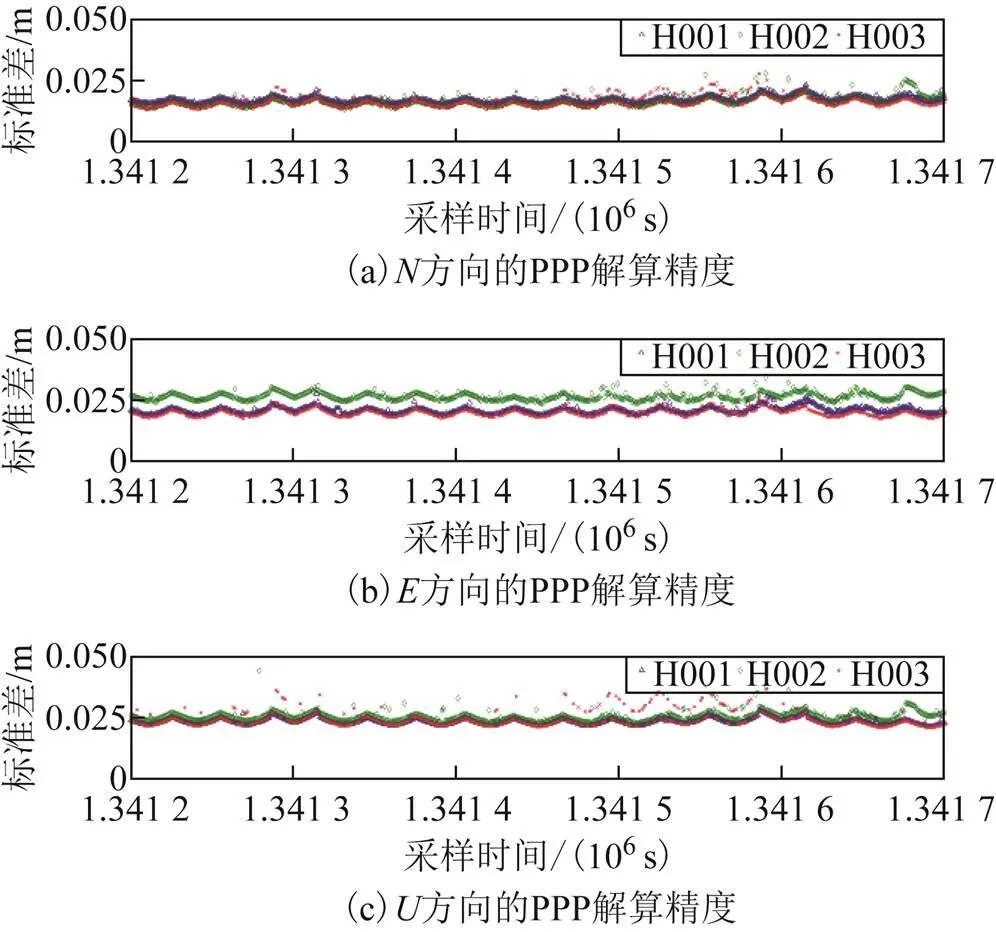
圖4 PPP解算精度

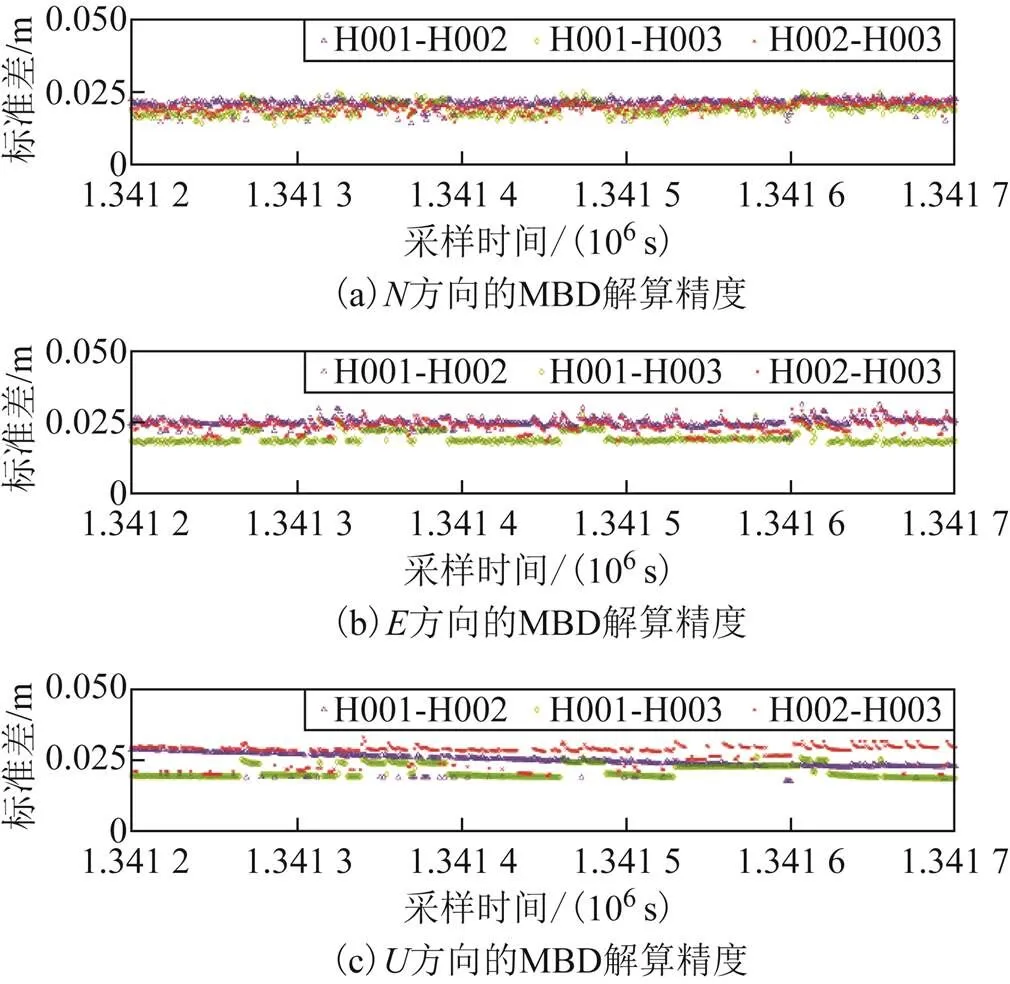
圖5 MBD解算精度

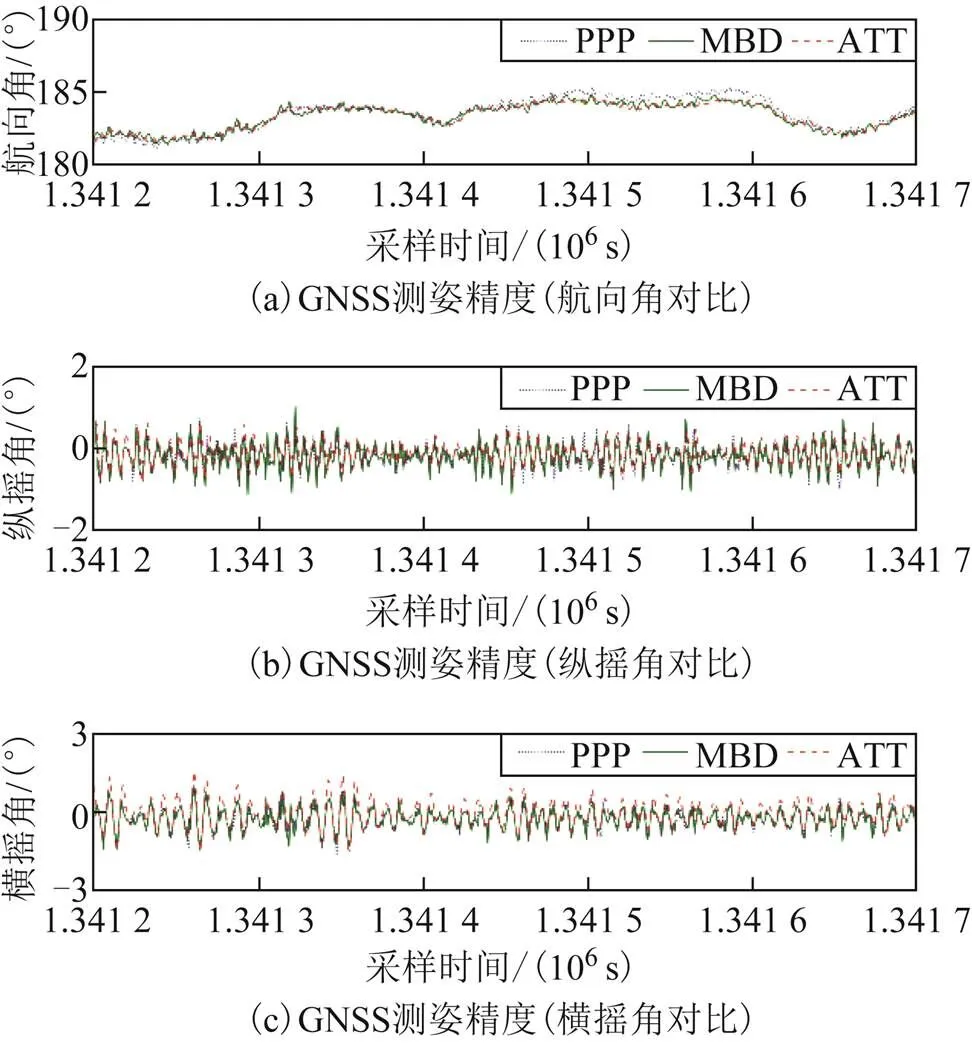
圖6 GNSS測姿精度對比

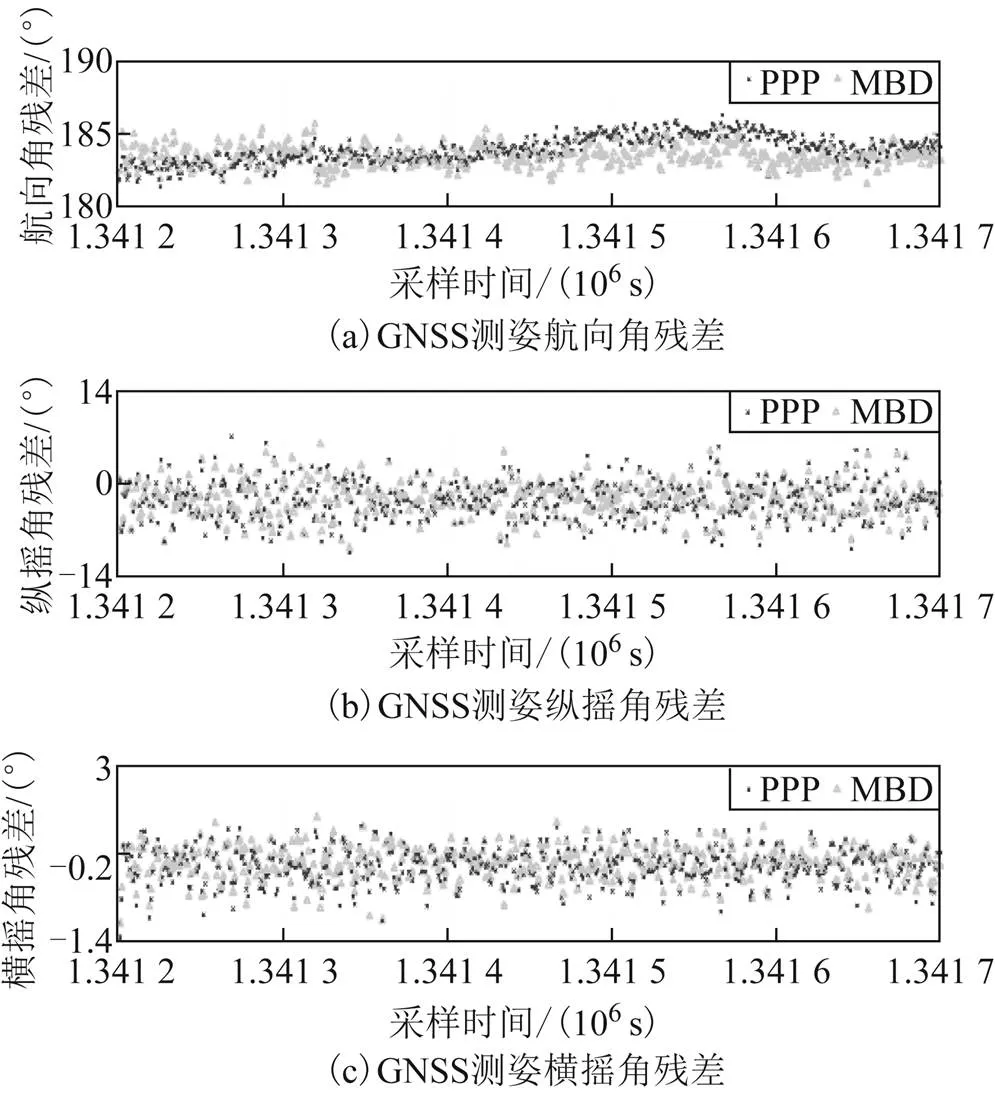
圖7 GNSS測姿殘差

表1 不同GNSS定位模型解算姿態參數標準差單位：°

由實驗結果分析可知：

1）由圖4可以看出，PPP解算平面定位精度可達厘米級，高程方向解算精度為分米級；根據圖5，MBD模式GNSS平面相對位置解算精度可達厘米級，高程方向相對位置解算精度普遍低于2 cm。顯然，MBD的相對定位精度要遠高于PPP，其對于船舶姿態計算具有良好的適用性。

2）由圖6可以看出，PPP及MBD解算模式下的測姿情況與Seapath 320高精度姿態測量系統測量結果變化趨勢吻合度較高；對于航向角、縱搖角、橫搖角，由圖7可以看出2種GNSS點位解算方式下的姿態計算結果與姿態儀測量結果差值均穩定在一定范圍內，且MBD的穩定性比PPP更好。

3）根據表1，MBD姿態解算的航向角、橫搖角、縱搖角，其標準差均小于PPP模式下的姿態計算結果。顯然對于遠海船姿測量，MBD點位解算精度及姿態解算精度均優于PPP模式，且因其特有的高精度基線解算結果，穩定性更高。其次，因GNSS誤差不隨時間累積，可靠性更高，所以與慣性測姿系統有很好的互補性，可以作為遠海測姿的有效補充。

4 結束語

本文旨在開展遠海GNSS 3天線船舶姿態測量方法研究，針對遠海無法采用SPP、RTK、PPK實現高精度GNSS測姿的問題，探索采用PPP、MBD進行遠海GNSS測姿。通過遠海GNSS 3天線船舶姿態測量實驗，分別用PPP及MBD解算數據進行姿態計算并與Seapath 320高精度姿態測量系統所測數據進行對比分析。實驗結果表明：PPP解算模式可以達到厘米級的平面精度和分米級的高程精度，但其收斂時間較長；而MBD解算模式下的相對精度明顯優于PPP，這也反映在測姿的結果中，MBD的測姿精度明顯優于PPP，且精度穩定，測姿誤差不隨時間累積。因此，基于MBD解算模式下的GNSS多天線船姿測量是提高遠海姿態觀測可靠性的有效方法。

[1] 陳曦. 基于MEMS慣性傳感器的高精度姿態測量關鍵技術研究[D]. 杭州: 浙江大學, 2014.

[2] ELLIS J F, CRESWELL G A. Interferometric attitude determination with the global positioning system[J]. Journal of Guidance & Control, 2015, 2(6): 96-102.

[3] BROWN A K, THORVALDSEN T P, BOWLES W M. Interferometric attitude determination using the global positioning system-a new gyrotheodolite[J]. Massachusetts Institute of Technology, 1981, 38(3): 99-102.

[4] HERMANN, BRUCE R. A simulation of the navigation and orientation potential of the Ti-Agr[J]. Marine Geodesy, 1985, 9(2): 133-143.

[5] EVANS A G. Roll, pitch, and yaw determination using a global positioning system receiver and an antenna periodically moving in a plane[J]. Marine Geodesy, 1986, 10(1): 43-52.

[6] 高源駿. GPS測姿算法與天線布局研究[D]. 哈爾濱: 哈爾濱工程大學, 2011.

[7] 張宏兵, 葛茂榮, 過靜珺. GPS姿態確定原理及軟件設計[J]. 測繪通報, 1999(12): 27-29.

[8] 過靜君, 葛茂榮. 適用于航天器的GPS姿態測量算法和軟件設計[J]. 清華大學學報（自然科學版）, 2000, 40(6): 99-102.

[9] HATCH R. Ambiguity resolution the fast lane[C]//The Institute of Navigation(ION). Proceedings of ION GPS-89, Second International Technical Meeting of the Satellite Division of The Institute of Navigation. Colorado: Colorado Springs, CO, 1989: 45-50.

[10] CRASSIDIS J L, MARKLEY F L. New algorithm for attitude determination using global positioning system signals[J]. Journal of Guidance, Control and Dynamics, 1997, 20(5): 891-896.

[11] LEFFERTS E J, MARKLEY F L, SHUSTER M D. Kalman filtering for spacecraft attitude estimation[J]. Journal of Guidance Control Dynamics, 1982, 5(5): 417-429.

[12] NADLER A, BAR-ITZHACK I Y, WEISS H. Iterative algorithms for attitude estimation using global positioning system phase measurements[J]. Journal of Guidance, Control and Dynamics, 2001, 24(5): 983-990.

[13] 王潛心. 機載GPS動態定位定速與定姿理論研究及軟件開發[D]. 長沙: 中南大學, 2011.

[14] 張鵬飛, 王發省, 辛明真, 等. 測船非勻速直線測量引起的多波束測深誤差分析[J]. 海洋測繪, 2018, 38(3): 30-34.

[15] 王發省, 張鵬飛, 辛明真, 等. GNSS船姿測量方法及對多波束測深精度的影響分析[J]. 海洋通報, 2018, 37(5): 529-536.

[16] 孫永榮, 劉建業, 陳武, 等. 多波束勘測中航向姿態系統研究[J]. 南京航空航天大學學報, 2003, 35(4): 356-360.

[17] 楊敏. 小型捷聯慣性導航系統研究[D]. 長沙: 中南大學, 2010.

Method of GNSS three-antenna far-sea vessel attitude measurement

WEI Jinjin1, XIN Mingzhen1, SHI Bo1, LIU Hui1, YANG Fanlin1,2

（1. College of Geodesy and Geomatics, Shandong University of Science and Technology, Qingdao, Shandong 266590, China; 2. Key Laboratory of Oceanic Surveying and Mapping, Ministry of Nature Resources, Qingdao, Shandong 266590, China）

Aiming at the problem that the GNSS-RTK high-precise relative positioning mode is not applicable because it is difficult to erect the base station on far-sea as the mode on the shore in the marine navigation attitude measurement, the paper proposed a far-sea attitude surveying method using GNSS: based on GNSS three antennas, the vessel attitude information was calculated by a direct solution, which could be used to directly solve the observed values with simple and little computation and no need to measure the baseline length in advance; and MBD and PPP were used to compute the attitude of GNSS three antennas; finally an experiment of far-sea attitude measurement was designed with the comparative analysis on the modes of MBD and PPP, taking the data of Seapath 320 high-precise attitude measurement system as reference. Results showed that the attitude measurement accuracy of MBD would be significantly higher than that of PPP with stable accuracy, indicating that MBD could be an effective method for improving the reliability of far-sea attitude measurement.

global navigation satellite system; attitude measurement; moving base station difference; precise point positioning; positioning error; accuracy of attitude measurement

P228

A

2095-4999(2020)03-0081-06

衛進進，辛明真，石波，等. GNSS三天線遠海船舶姿態測量方法[J]. 導航定位學報, 2020, 8(3): 81-86.（WEI Jinjin, XIN Mingzhen, SHI Bo, et al. Method of GNSS three-antenna far-sea vessel attitude measurement[J]. Journal of Navigation and Positioning, 2020, 8(3): 81-86.）

10.16547/j.cnki.10-1096.20200313.

2019-12-03

國家重點研發計劃項目（2016YFB0501700，2016YFB0501705）。

衛進進（1997—），男，山西運城人，碩士研究生，研究方向為海洋定位導航。

陽凡林（1974—），男，湖北荊州人，博士，教授，研究方向為海洋測繪、大地測量等。