不同作業模式下的GNSS/聲學聯合定位模型

鄺英才，呂志平，王方超，許 煒

不同作業模式下的GNSS/聲學聯合定位模型

鄺英才，呂志平，王方超，許 煒

（信息工程大學 地理空間信息學院，鄭州 450001）

為彌補目前全球衛星導航系統（GNSS）/聲學聯合解算研究中的不足，提出1種海底控制點布設的聯合定位模型：給出觀測過程統一并顧及基準轉換的GNSS/聲學聯合定位原理，并在不同作業距離、不同應答器數量條件下，推導出聯合模型相應的數學模型；最后以分層等梯度聲速跟蹤終點位置為參考，通過實測數據進行驗證。結果表明，當水下觀測數據質量及數量受限時，較之傳統多步求解法，聯合定位法能得到更高的定位精度。

底控制點；全球衛星導航系統；GNSS/聲學；聲速跟蹤；基準轉換；多源融合

0 引言

隨著經略海洋戰略的制定，建設可靠的海洋大地基準已迫在眉睫[1-2]。作為組成海洋大地測量控制網的關鍵一環，海底控制點高精度3維坐標的確定，成為近年來海洋測繪領域的熱點[3-7]。美國在20世紀80年代，就基于全球衛星導航系統（global navigation satellite system, GNSS）在海洋測繪中應用的諸多優勢，提出利用水下聲學定位技術結合GNSS海面定位技術，對海底點進行觀測標定[8]。現階段被廣泛認可的是利用可控航跡的測量船，搭載測量設備及相關傳感器進行觀測的實施方案，該方案以測量船為樞紐，通過距離交會確定全球坐標框架下海底控制點的絕對坐標。

復雜海洋環境以及多類觀測信息的融合，勢必會帶來更多潛在誤差的影響[9]。為削弱組合定位中的各類誤差，國內外學者從不同方面展開了研究。從觀測量獲取角度考慮，海面GNSS定位根據作業距離長短，可以選擇與岸基基準站差分定位或深遠海動態精密單點定位（precise point positioning, PPP）[10]。文獻[11]論證了優化航跡的實質，是改善聲學觀測空間的幾何結構，進而提高聲學定位精度；文獻[12]根據背景聲速剖面誤差和聲速長周期系統誤差的特點，設計了多應答器中垂線航跡，通過應答器間作差分，可以消除相關誤差。從數據處理角度考慮，可以將重要誤差項參數化[13]，或采用更貼近誤差變化特點的精化模型[14]，此外還有學者[15]利用聲學初始入射角，來完善水下定位隨機模型。針對控制點垂直方向精度不高這一難點，目前大多通過加入換能器至應答器的高精度深度差測量值，來約束原始測距方程[16]，提升點位精度。上述研究在解算待求點坐標時，均將海面及海面以下觀測過程分開處理，考慮到水下觀測精度日益趨近海面GNSS觀測精度，文獻[17-18]提出，可以通過函數關系及觀測量間權比的準確描述，將GNSS觀測信息、姿態信息、水下聲學觀測信息等相結合進行整體處理。近年來，包容多種測量手段、強調多源數據融合的綜合定位、導航、授時（positioning, navigation and timing, PNT）體系逐步發展[19]，可以預見，建立統一觀測信息的GNSS/聲學聯合定位模型，將會構成建立我國海洋大地測量控制網的重要理論基礎。

已有研究對GNSS/聲學聯合定位的基礎理論進行了探討，但是模型建立尚存在許多可擴展的細節。針對目前研究的不足，本文細化在近海、深遠海域，單應答器、多應答器等不同實驗條件下，對應的GNSS/聲學聯合定位模型，以期為相關研究提供參考。

1 GNSS/聲學聯合定位原理

1.1 海面及水下觀測過程

隨著GNSS全球化發展進程的加快，衛星定位技術正逐漸融入海洋測繪領域的諸多重要環節。雖然海面利用電磁波測量簡便且可靠，但其在水下的傳播會出現嚴重衰減，無法支撐正常的測量工作；因此，目前水下基本依靠聲脈沖信號進行目標測距。基于此思想，各國開始嘗試結合GNSS定位技術和聲學定位技術，建立海底控制點，其觀測過程如圖1所示。

作為整個觀測過程的樞紐，測量船需要提前規劃好航行軌跡，相較于浮標或早期實驗船的漂浮策略，可以在避免過多冗余數據的同時，保證良好的觀測空間幾何結構，削弱聲學測距誤差。測量船搭載GNSS天線進行實時GNSS動態觀測，若在近岸海域，通常需再設立岸基基準站進行同步觀測。此外，船上還需搭載定向羅經、姿態測量、鹽溫深（conductivity temperature depth，CTD）測量等傳感器。若采用最常用的長基線水聲定位方法，則船體底部應安置單探頭收發換能器裝置，與海底應答器進行聲脈沖信號傳輸。通過采集GNSS觀測信息、姿態觀測信息、聲速剖面觀測信息、水位計觀測信息、聲學觀測信息等，實現海面基準傳遞至海底控制點。

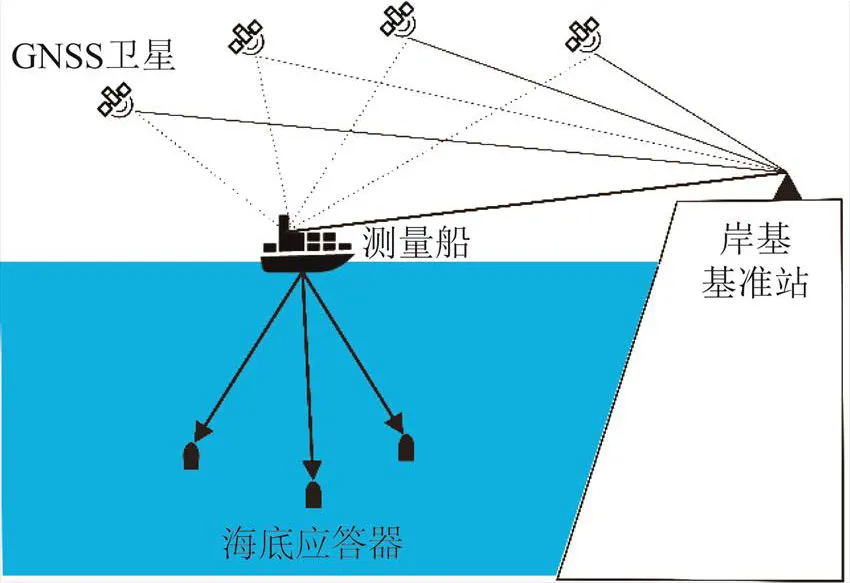
圖1 GNSS/聲學聯合觀測過程

1.2 船體坐標系

海面GNSS動態定位可以得到全球坐標框架下的天線中心坐標；但與海底應答器建立聯系的船底收發換能器中心與其并不重合，還需要進行基準轉換。考慮到水位計測量值等在局部坐標系下討論更為直觀，故須引入2種船坐標系。

選擇船體上某點作為坐標系原點（通常為與海面相切的船重心），軸指向測量船前進方向，軸垂直于平均海平面向下，軸與軸共平面，指向符合右手坐標系，稱此時建立的坐標系為船體水平坐標系，又稱船體標準坐標系。此坐標系建立在測量船理想航行狀態的基礎上，認為坐標軸指向恒不變。然而受風浪等海洋環境影響，測量船在航行過程中時刻發生著姿態或航向的變化，因此需要建立更符合實際運動狀態的坐標系。約定坐標系原點不變，軸指向船艏，軸指向右舷坐標軸，軸垂直于船體向下，此時的局部坐標系即為船體坐標系。由于船體坐標系在航行過程中跟隨船體姿態實時變化，故姿態變化是在船體坐標系下而不是船體水平坐標系下進行討論的；事實上，測量船進行作業之前，需要進行各傳感器測量中心的相對位移標定，按照定義，標定值所屬坐標系也應為船體坐標系。

1.3 海面基準轉換

GNSS/聲學聯合定位模型將海面觀測與水下聲學觀測聯合求解。為了建立GNSS天線中心坐標與海底應答器坐標之間的聯系，就需要在同1個函數模型中對海面基準轉換進行準確描述。

根據2種船坐標系的定義可以發現，對船體坐標系下各參考點的相對偏移進行橫搖角、縱搖角、航向角3種姿態角轉化，則可以將其轉換至船體水平坐標系下；再根據全球坐標框架與局部坐標系之間的坐標旋轉關系，可將船體水平坐標系下的參考點偏移轉換至全球坐標框架下；最后結合觀測得到的GNSS天線中心地理坐標，即可得到其他參考點（如換能器）在全球坐標框架下的絕對地理坐標。上述過程可以表示為

2 不同作業模式下的GNSS/聲學聯合定位數學模型

2.1 作業模式1（深遠海域+單應答器布設）

海洋廣袤無垠的特點，使陸地上部分技術手段無法直接應用于海洋測繪領域。在距離海岸上百千米的深遠海域，因遠遠超出可靠的作業距離范圍，很難依靠海面動態差分定位；應改用不受作業距離限制的船載動態PPP模式。為保證時間的同步性，水下采用幾何定位法，并加入基準轉換方程，將海面與水下觀測方程聯系起來。此時GNSS/聲學聯合觀測模型可以表示為

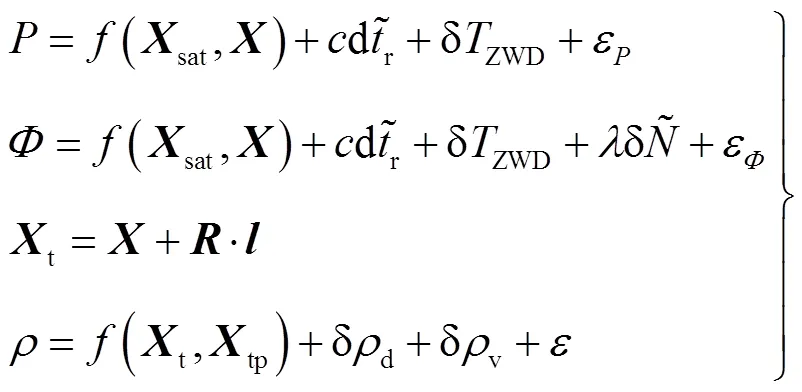
為提高垂直解精度，可以利用相對更高觀測精度的水位計壓力深度值對觀測模型進行約束[16]。結合式（1），可以推導出在船體水平坐標系下，換能器至應答器的深度差公式，即約束方程為

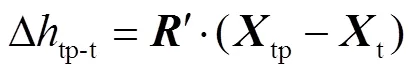
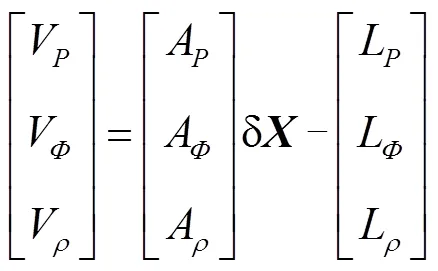
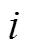
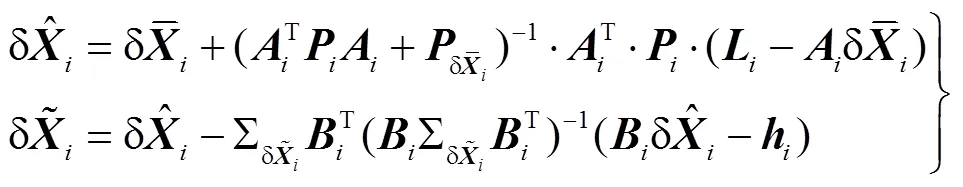
由以上分析可知，在深遠海域對海底單應答器進行定位時，GNSS/聲學聯合定位模型的狀態向量具體形式應為

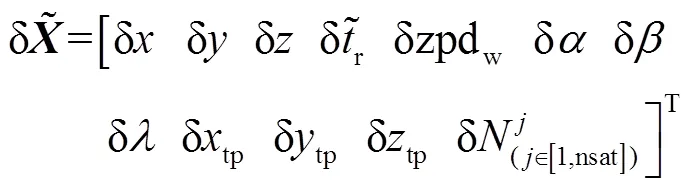
2.2 作業模式2（深遠海域+多應答器布設）

考慮到遠海測量高成本、多耗時的特點，對于深遠海域多應答器位置的確定，將是未來海洋基準研究的重點。該作業條件下，仍可以按照上節方案，將各應答器單獨進行處理，但效率較低。此時可以利用多應答器同步信號傳輸的特點，優化測量船航跡，在應答器間進行水下差分，消除部分聲學測距誤差[21]。

以雙應答器為例，若通過合理規劃航跡，使2個應答器的信號傳輸距離在本次航行過程中始終一致，則可以將同歷元觀測方程進行差分，以達到消除部分聲速測距誤差的目的。經過差分組合，式（2）中的水下聲學信號觀測方程改寫為

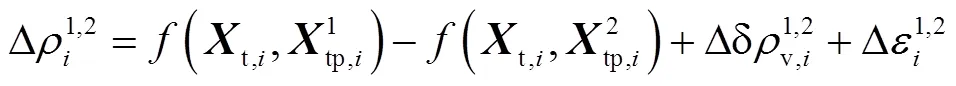
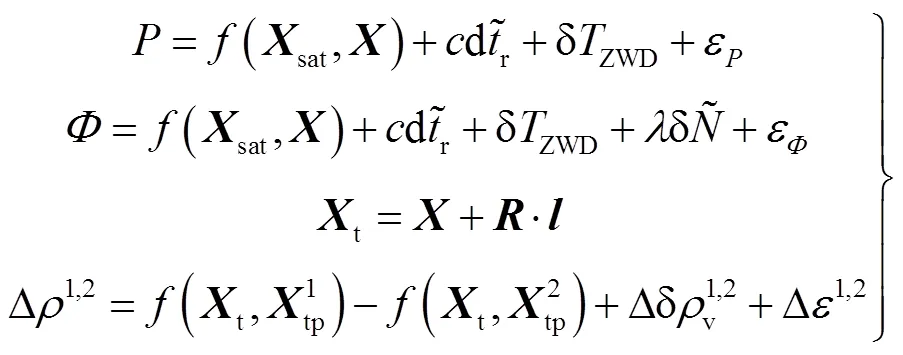
相應地，約束方程變為2維形式

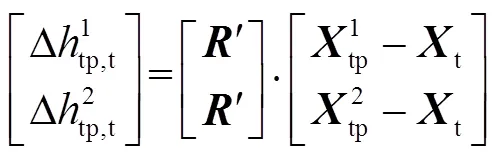
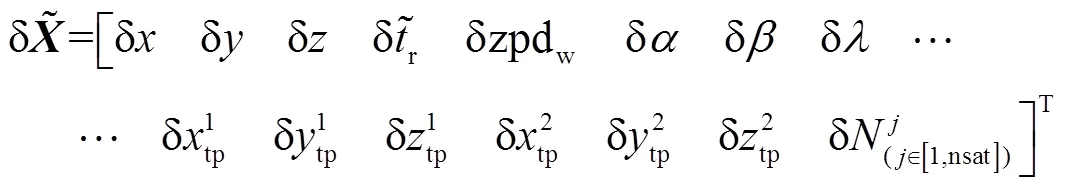
從狀態向量的構成可以發現：采用此模型定位深遠海域多應答器位置時，待估參數較多；一方面應該保證有適量必要觀測數據，避免平差秩虧問題，另一方面應實時關注動力學擾動造成的參數異常問題，可以通過引入自適應濾波方法削弱其影響[22]。

2.3 作業模式3（近岸海域+單應答器布設）

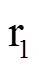
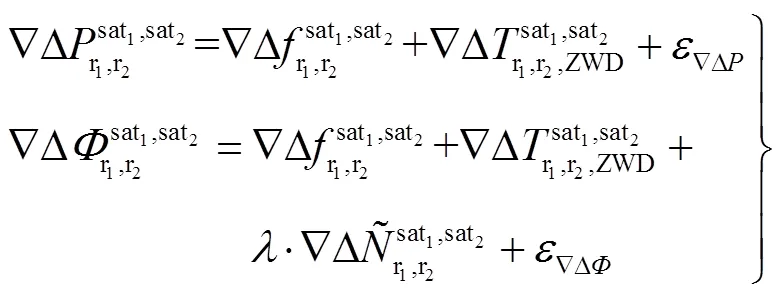
將式（2）中海面觀測方程替換為式（11），并聯立式（3），即為該作業模式下GNSS/聲學聯合定位觀測模型，待估狀態參數向量為

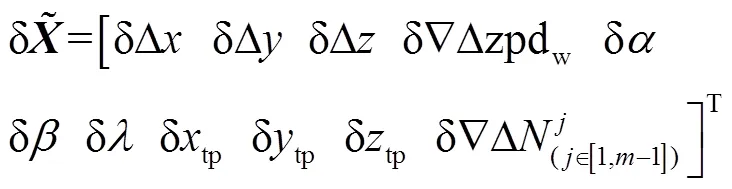
2.4 作業模式4（近岸海域+多應答器布設）

在上述分析的基礎上，海面與岸基基準站進行動態差分定位，水下在各應答器間進行差分定位；結合合理規劃的測量船航跡，可以直接得到該作業模式下GNSS/聲學聯合定位觀測方程為

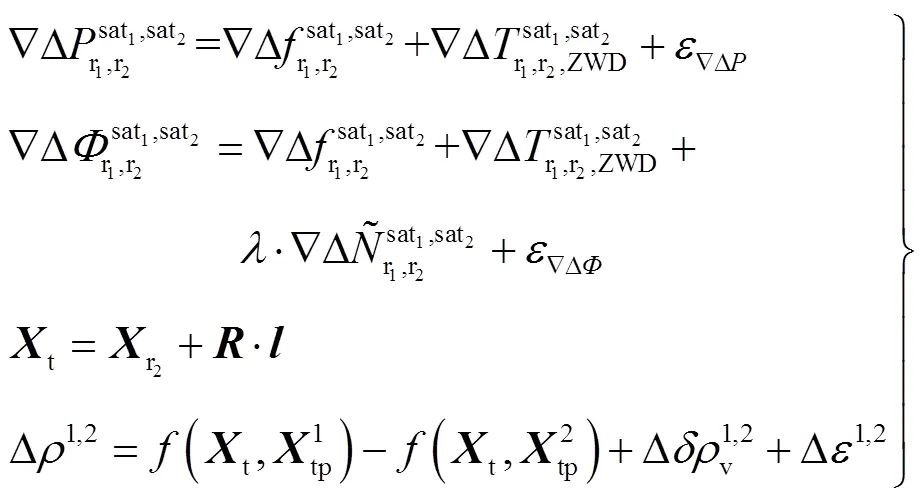
約束方程形式與式（9）一致。相應地，此時誤差方程待估狀態向量具體形式為

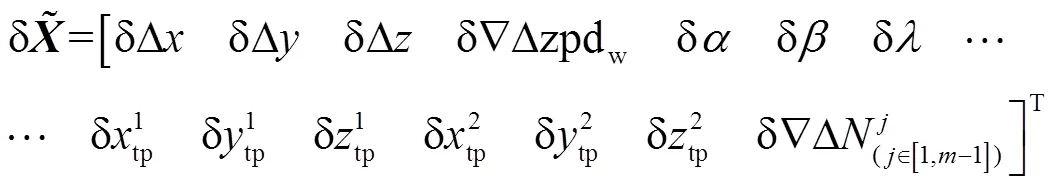
3 實驗與結果分析

基于以上理論推導和實測實驗特點，對在深遠海域單應答器布設作業模式下，GNSS/聲學聯合定位模型效果進行了實驗驗證與分析。為得到高精度應答器的絕對位置，作為與模型定位結果的對比參考量，本文首先對各類實測數據進行預處理，并利用分層等梯度聲速跟蹤得到聲線波束腳印坐標。

3.1 波束腳印位置計算

本文采用的實測數據來自膠州灣口海域實驗的后處理結果。實驗的日期為2018-10-11，測量船搭載全球定位系統(global positioning system, GPS）天線、聲速剖面儀、電羅經、加拿大Applanix公司的POS-MV定位定姿系統等傳感器，測量船在該海域進行了時長約為35 min的海上觀測，如圖2所示。測區水深約18 m。水下布設了1個應答器，利用安裝在船底的聲學基陣，對應答器進行標定。基陣與姿態傳感器、姿態傳感器與GPS天線、測量船重心與姿態傳感器之間的相對位置關系已精確測定。船載基陣和應答器處各固定了1個水位計，水位計至基陣中心、應答器中心至應答器水位計的垂直距離已提前測量，水位計提供世界協調時（universal time coordinated，UTC）、水溫、壓強和深度信息。聲速剖面儀測量了該水域的聲速剖面，包括聲速、水溫、深度信息。

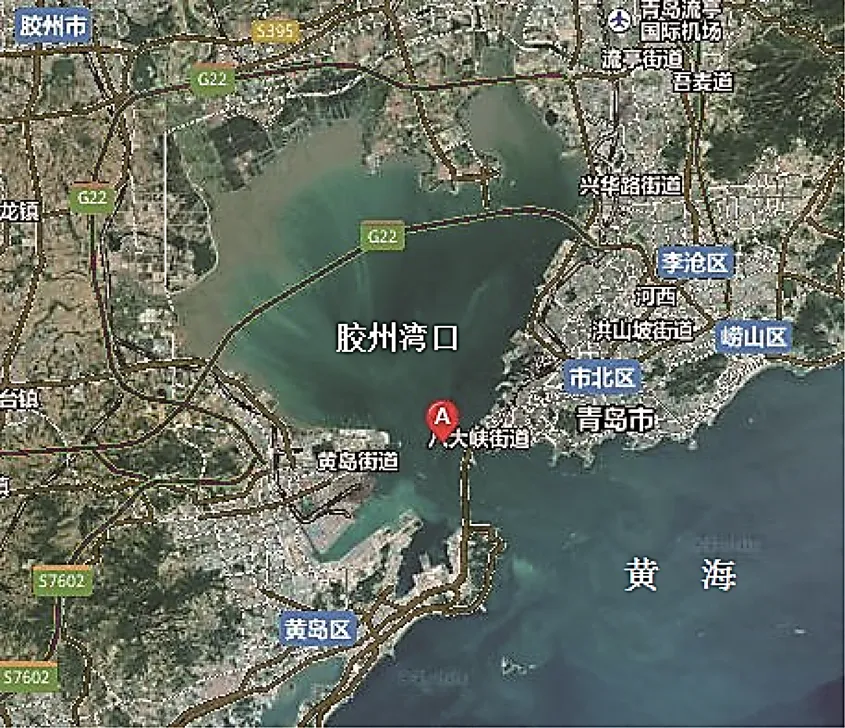
圖2 測區位置

原始測量數據包括姿態傳感器測量文件、GPS觀測文件、聲線基陣觀測文件、水位計數據、聲速剖面數據。其中，姿態測量文件可以用Applanix公司配套處理軟件，提取出后續處理需要的姿態角等信息。而GPS觀測數據提供了水下定位的水面基準，若其不可靠，將會嚴重影響應答器定位精度。本文采用高精度GNSS數據處理軟件Rtklib動態定位模塊，結合精密星歷、精密鐘差、偽碼偏差（differenced code bias，DCB）文件、天線改正文件等，對測量船數據進行預處理，得到逐歷元的船位坐標。利用以上數據信息進行分層等梯度聲線跟蹤，可以得到高精度的應答器坐標。

1）水位計數據處理。原始數據包括船載基陣處的深度數據和海底應答器處的深度數據，基陣深度和應答器深度的計算公式為

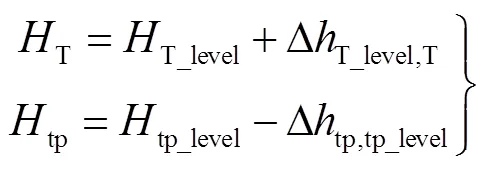
2）聲速剖面數據處理。按照分層后，層內聲速變化等梯度的原則，將原始聲速剖面進行分層處理，由于后續處理時需要聲速迭代初始值，需提前計算加權平均聲速。實測聲速剖面如圖3所示。

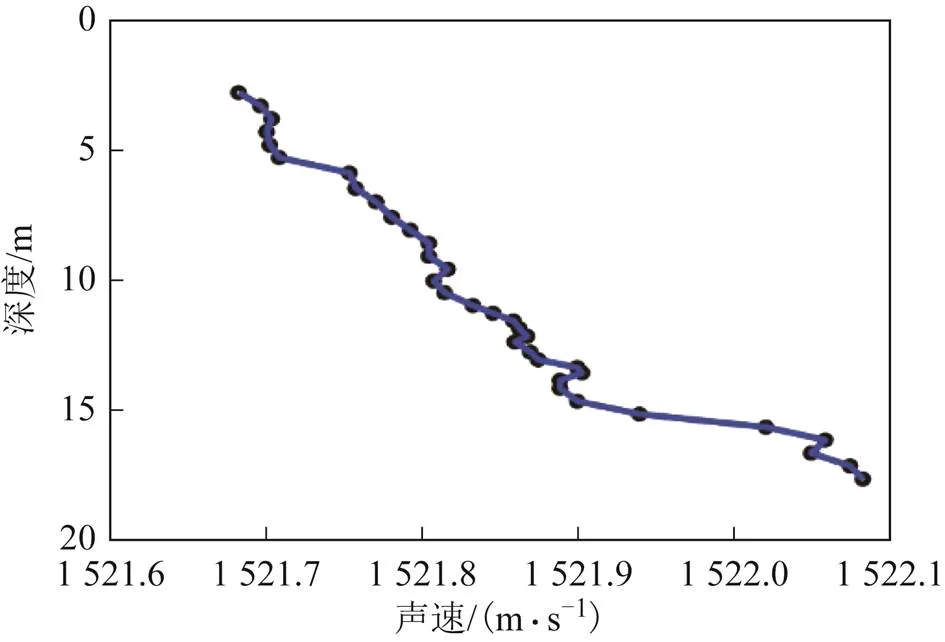
圖3 實測聲速剖面曲線

3）解算應答器概略坐標。因為布設應答器時，未進行提前標定，故應答器概略坐標是未知的；而聲速跟蹤模型需要應答器概略坐標作為近似值參與解算，因此需要利用聲基陣觀測數據粗略求解應答器坐標。解算時，采用長基線定位系統處理單應答器模式時的定位方法，利用多個測量船船位實現應答器坐標解算。需要注意的是，GPS動態PPP結果是船載天線中心的坐標，而水下定位需要的是船底基陣中心的坐標；這就需要通過坐標系轉換對基陣坐標進行改化。由于GPS觀測數據采樣率與聲基陣觀測采樣率也不相同，改化后的基陣中心坐標序列仍需要進行插值處理。對所有歷元的觀測數據進行最小二乘平差后，可以得到應答器概略坐標。考慮到平差中使用了近似坐標，可以進行迭代平差以保證結果精度。

4）表層入射角精化。實際處理時發現：隨著測量船的航行，部分歷元基陣中心至應答器較遠，此時其表層入射角將變大；當角度過大時，逐層計算的聲線入射角可能不再是實數，即入射角計算發散。為避免這個問題，可采用改進表層入射角迭代計算公式[23]，即

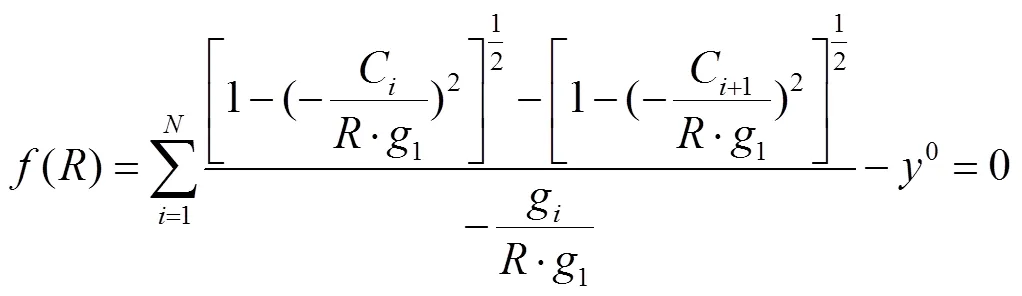
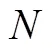
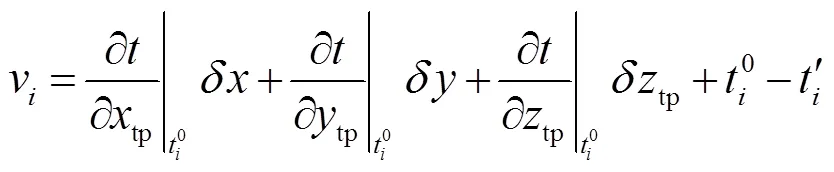
3.2 聯合模型定位結果分析

基于自編GNSS/聲學聯合定位解算軟件原型，對膠州灣口數據進行了處理，觀測模型設置與2.1節相同，采用卡爾曼濾波進行參數估計，逐歷元得到應答器3維坐標；另按照傳統多步求解方法設計對比方案：船位坐標采用Rtklib軟件動態差分定位模塊逐歷元解算結果，在不考慮姿態誤差的情況下，通過基準轉換得到逐歷元換能器坐標，參與水下定位解算。利用實測聲速剖面得到加權平均聲速，與觀測時延相乘作為逐歷元的水下測距觀測值，測距誤差設為0.3 %倍的斜距觀測值，采用最小二乘法進行迭代平差解算。以聲速跟蹤結果作為2種方案解算結果的對比參考值，將多步求解法結果與聲速跟蹤結果作差，統計各方向上的絕對差值分量為1.591、2.545、2.387 m；將聯合定位結果與聲速跟蹤結果作差得到偏差序列，統計序列的標準差（standard deviation，STD），各方向上的STD值分別為1.073、0.782、1.812 m。

分析統計結果數據可知：受限于水下實測觀測數據質量及數量，較之精度較高的聲速跟蹤結果，本實驗中多步求解法最小二乘解算結果并不理想；而此時GNSS/聲學聯合定位方法相對更具優勢，因其函數模型較準確地描述了衛星端至海底應答器的觀測過程，通過對GNSS信息、水下聲學信息、姿態信息等觀測量在同一數學模型中進行統一處理，一定程度上改善了單一觀測量可能造成的精度損失問題。由于我國海底控制點布設尚處于實驗階段，實測數據較少，GNSS/聲學聯合定位模型在其他幾種作業模式下的應用效果還有待在后續研究中進行驗證。

4 結束語

如今，多源觀測信息融合技術在海洋測繪中的重要性愈發明顯。針對目前海底控制點布設中的研究不足，在利用走航式測量船進行海面及水下觀測的基礎上，本文顧及不同海域、不同數量應答器的實驗條件特點，分別推導了不同作業模式下的GNSS/聲學聯合定位數學模型，并基于實測數據進行了初步驗證，得出以下結論：

1）分層等梯度聲速跟蹤模型計算細節較多，但刻畫的曲線能逼近最真實的聲線傳播路徑，故

其跟蹤得到的波束終點位置具有較高的精度。

2）GNSS/聲學聯合定位模型顧及各類觀測信息對海底控制點定位過程的貢獻，合理準確地描述相互間的函數關系，使得聯合衛星和聲學觀測信息解算海底控制點成為可能。在水下觀測數據質量不高或數量較少的情況下，較之傳統多步求解法，本文提出的方法可以得到更高精度的應答器定位結果。

下一步研究需要對不同作業模式下的聯合定位模型進行細節精化，如引入抗差估計和自適應選權濾波算法，削弱觀測粗差和動力學異常的影響，再如各類傳感器間的時間配準問題等，避免不必要的精度損失，進一步改善聯合濾波效果。

[1] 楊元喜, 徐天河, 薛樹強. 我國海洋大地測量基準與海洋導航技術研究進展與展望[J]. 測繪學報, 2017, 46(1): 1-8.

[2] 劉經南, 陳冠旭, 趙建虎, 等. 海洋時空基準網的進展與趨勢[J]. 武漢大學學報(信息科學版), 2019, 44(1): 20-40.

[3] OBANA K, KATAO H, ANDO M. Seafloor positioning system with GPS-acoustic link for crustal dynamics observation[J]. Earth, Planets and Space, 2000, 52(6): 415-423.

[4] XU P, ANDO M, TADOKORO K. Precise, three-dimensional seafloor geodetic deformation measurements using difference techniques[J]. Earth, Planets and Space, 2005, 57(9): 795-808.

[5] FUJITA M, ISHIKAWA T, MOCHIZUKI M, et al. GPS/acoustic seafloor geodetic observation: method of data analysis and its application[J]. Earth, Planets and Space, 2006, 58(3): 265-275.

[6] BALLU V, BOUIN M N, CALMANT S, et al. Absolute seafloor vertical positioning using combined pressure gauge and kinematic GPS data[J]. Journal of Geodesy, 2010, 84(1): 65.

[7] CHEN H H, WANG C C. Optimal localization of a seafloor transponder in shallow water using acoustic ranging and GPS observations[J]. Ocean Engineering, 2007, 34(17/18): 2385-2399.

[8] SPIESS F N. Analysis of a possible sea floor strain measurement system[J]. Marine Geodesy, 1985, 9(4): 385-398.

[9] 鄺英才, 呂志平, 蔡汶江, 等. GNSS/聲學系統定位精度影響因素分析[J]. 測繪通報, 2018 (12): 15-20, 45.

[10] GENG J, TEFERLE F N, MENG X, et al. Kinematic precise point positioning at remote marine platforms[J]. GPS Solutions, 2010, 14(4): 343-350.

[11] SATO M, FUJITA M, MATSUMOTO Y, et al. Improvement of GPS/acoustic seafloor positioning precision through controlling the ship’s track line[J]. Journal of Geodesy, 2013, 87(9): 825-842.

[12] SUN Wenzhou, YIN Xiaodong, ZENG Anmin. The relationship between propagation time and sound velocity profile for positioning seafloor reference points[J]. Marine Geodesy, 2019, 42(2): 186-200.

[13] ZHAO Jianhu, ZOU Yajing, ZHANG Hongmei, et al. A new method for absolute datum transfer in sea?oor controlnetwork measurement[J]. Journal of Marine Science and Technology, 2016, 21(2): 216-226.

[14] 孫文舟, 殷曉冬, 暴景陽, 等. 海底控制點定位的半參數平差模型法[J]. 測繪學報, 2019, 48(1): 117-123.

[15] 趙爽, 王振杰, 劉慧敏. 顧及聲線入射角的水下定位隨機模型[J]. 測繪學報, 2018, 47(9): 1280-1289.

[16] 趙建虎, 陳鑫華, 吳永亭, 等. 顧及波浪影響和深度約束的水下控制網點絕對坐標的精確確定[J]. 測繪學報, 2018, 47(3): 413-421.

[17] Kuang Yingcai, LYU Zhiping, Wang Junting, et al. The GNSS/acoustic one-step positioning model with attitude parameters[C]//The Academic Exchange Center of China Satellite Navigation System Administration Office.Proceedings of 2019 China Satellite Navigation Conference (CSNC 2019). Singapore: Springer, 2019: 479-489.

[18] 鄺英才, 呂志平, 陳正生, 等. 基于方差分量估計的多模GNSS/聲學聯合定位方法[J]. 中國慣性技術學報, 2019, 27(2): 181-189.

[19] 楊元喜. 綜合PNT體系及其關鍵技術[J]. 測繪學報, 2016, 45(5): 505-510.

[20] SIMON D. Kalman filtering with state constraints: a survey of linear and nonlinear algorithms[J]. IET Control Theory& Applications, 2010, 4(8): 1303-1318.

[21] 孫文舟, 殷曉冬, 曾安敏, 等. 附加深度差和水平距離約束的深海控制點差分定位算法[J]. 測繪學報, 2019, 48(9)：1190-1196.

[22] 鄺英才, 呂志平, 李林陽, 等. 自適應選權濾波在GNSS/聲學定位模型中的應用[C]//錢學森空間技術實驗室. 中國慣性技術學會高端前沿專題學術會議: 天空海一體化水下組合導航會議論文集. 北京: 中國慣性技術學會, 2017: 117-129.

[23] 王振杰, 李圣雪, 聶志喜, 等. 水聲定位中一種大入射角聲線跟蹤方法[J]. 武漢大學學報（信息科學版）, 2016, 41(10): 1404-1408.

Study on GNSS/acoustic joint positioning model under different measurement schemes

KUANG Yingcai, LYU Zhiping, WANG Fangchao , XU Wei

（Institute of Geography and Spatial Information, Information Engineering University, Zhengzhou 450001, China）

In order to supplement the insufficiency in current study on the joint solution of GNSS/acoustics, the paper proposed an integrated positioning model for the layout of submarine control points: the principle of GNSS/acoustic joint positioning with unified observation process and reference conversion was given, and the corresponding mathematical model of the joint positioning was derived under the condition of different surveying distances and amounts of transponders; finally based on the tracking ending point location with the layered equal-gradient acoustic velocity, the measured data were used in test. Result showed that the proposed method could obtain higher positioning accuracy than the traditional multi-step method when the quality and quantity of underwater observation data are limited.

submarine control points; global navigation satellite system (GNSS); GNSS/acoustic; acoustic velocity tracking; datum transformation; multi-source fusion

P228

A

2095-4999(2020)03-0040-07

鄺英才，呂志平，王方超，等. 不同作業模式下的GNSS/聲學聯合定位模型[J]. 導航定位學報,2020,8(3): 40-46.（KUANG Yingcai, LYU Zhiping, WANG Fangchao, et al. Preliminary study on GNSS/acoustic joint positioning model under different measurement schemes[J]. Journal of Navigation and Positioning, 2020, 8(3): 40-46.）

10.16547/j.cnki.10-1096.20200306.

2019-12-02

鄺英才（1994—），男，四川成都人，博士研究生，研究方向為測量數據處理理論與方法。