一種基于近景攝影測量的三軸氣浮臺連續姿態測量方法

張繼超，蘭文琦，金澤林，楊雄丹，周沛希，劉建程

一種基于近景攝影測量的三軸氣浮臺連續姿態測量方法

張繼超，蘭文琦，金澤林，楊雄丹，周沛希，劉建程

（遼寧工程技術大學 測繪與地理科學學院，遼寧 阜新 123000）

針對3自由度氣浮仿真實驗平臺的姿態測定中，現有測量手段對氣浮臺空間占用較大，導致縮減了氣浮臺可用負載的問題，提出1種基于近景攝影測量的3軸氣浮臺連續姿態測量方法：分析氣浮平臺姿態測定的任務需求，采用10參數模型對高精度工業相機進行標定；在氣浮平臺布設人工標志點，通過臺體坐標系將相機坐標系下的測量值轉換到真北基準下，完成氣浮仿真裝置姿態測量平臺的搭建，實現對氣浮臺的連續動態測量。實驗結果表明，該方法在3軸方向的重復測量誤差，均優于設計的10″容差值，證明具有可行性和有效性，可以為降低航天器系統的研制風險提供參考。

3軸氣浮臺；近景攝影測量；標定；真北基準；姿態角測量

0 引言

隨著航空航天技術的飛速發展，對航天器姿態穩定性和控制水平的要求也大幅提高。要制造更精密且結構復雜的航天器控制系統，不僅對航空航天制造技術提出了較高要求，而且對精確測定航天器在太空失重環境下的位置姿態也是一項巨大的挑戰。氣浮仿真實驗平臺能夠模擬衛星本體在失重環境下的運動狀態，并利用特定的測量手段，精確地測定仿真平臺在任意時刻的空間姿態信息，從而對航天器系統進行評估[1-2]。

目前，根據氣浮臺姿態測定的需求，國內有些學者提出了基于伺服測角系統、感應同步器、傾角儀傳感器等氣浮臺姿態測量方案，但這些系統都具有復雜的機械結構和敏感器部件，對氣浮臺空間占用較大，從而縮減了氣浮臺的可用荷載[3-4]。文獻[5]提出了“陀螺加傾角傳感器”（micro electro mechanical systems, MEMS）的姿態測定系統，通過采集低精度輸出的MEMS陀螺儀角速度和高精度的傾角傳感器數據，利用擴展卡爾曼濾波器進行角速度和角度數據處理，從而得到氣浮臺在3軸方向上的位姿信息。文獻[6]為解決氣浮臺偏航軸轉角難以精確測量的問題，提出通過室內星敏感器模擬仿真，進行氣浮臺3軸姿態角的測定方法。文獻[7]通過視覺測量的方法，將光電耦合器（charge coupled device, CCD）相機安裝在氣浮臺臺面上，在臺體上方布置1種非同心圓對的特征標靶，經過實驗分析得出氣浮臺3軸姿態角、光心與平面標靶距離最大相對誤差分別小于0.02 %和0.008 %。文獻[8]為實現對3軸氣浮臺姿態的控制，嘗試采用模型預測控制器的方式，以1種非線性跟蹤微分器作為觀測器，在控制器的配合下，0同對氣浮臺自由飛行與定點懸浮、矩形軌跡跟蹤、圓形跟蹤等運動進行仿真實驗，通過與比例積分微分（proportion integration differentiation, PID）控制器進行對比，結果顯示PID控制效果相對較好，但前者也顯示出控制過程更加平穩直接、抗干擾能力強等優點。文獻[9]提出了1種基于單目視覺的氣浮臺位姿測量方法，通過設計1種具有旋轉、平移、縮放不變形的圓形靶標，在待識別區域內通過“行、列”掃描算法，實現靶標點圓心快速定位，并結合計算機系統下的圓心位置與視覺測量系統中的坐標轉換關系，完成氣浮臺實際位姿的解算。

本文采用近景攝影測量方法，來解決氣浮臺姿態測量問題，實現了氣浮臺的連續動態監測。近景攝影測量方法因其具有信息容量大、非接觸、操作簡便、快速高效、易儲存和不易受溫度變化、振動等外界因素干擾的特點，已經廣泛地應用到了大型工業測量領域中[10]。將近景攝影測量方法應用到3自由度氣浮仿真實驗平臺的姿態角測量中，則是1種對氣浮臺姿態測量的新嘗試。

本方法是在氣浮臺上布設人工標志點，搭建氣浮臺仿真裝置姿態測量平臺。采用高精度的相機標定方法和立方鏡光學準直技術，分別標定測量氣浮臺姿態的相機和臺體的真北基準。

1 相機標定

氣浮仿真平臺姿態測量的精度要求是，3軸方向的角度重復測量誤差不超過10″。相機標定是影響近景攝影測量精度的主要因素之一，用標定參數修正后，能有效減弱鏡頭的光學畸變與相機系統誤差。

1.1 相機待標定的10參數模型

為使共線方程成立，必須考慮像點坐標偏差。圖像中任意點的系統性誤差可以歸納為徑向、偏心、像平面和內方位元素等導致的畸變誤差，考慮像點系統誤差的存在，共線條件方程[10]最終形式為

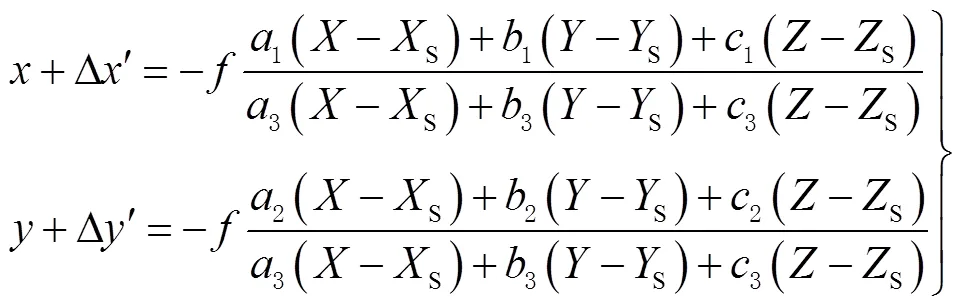
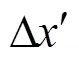
假定平面標定板在世界坐標系中的坐標為0，在2個以上位置對標定版進行采集，基于線性模型計算得出攝像機參數的1個優化解，考慮徑向誤差和切向誤差構造目標函數，然后基于最大似然法進行非線性求解，能有效減弱鏡頭的光學畸變與相機系統誤差的影響。采用改進的10參數模型進行相機標定，像點坐標誤差方程式可由式（1）經過線性化得

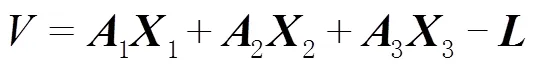
其余各參數相應的系數矩陣為

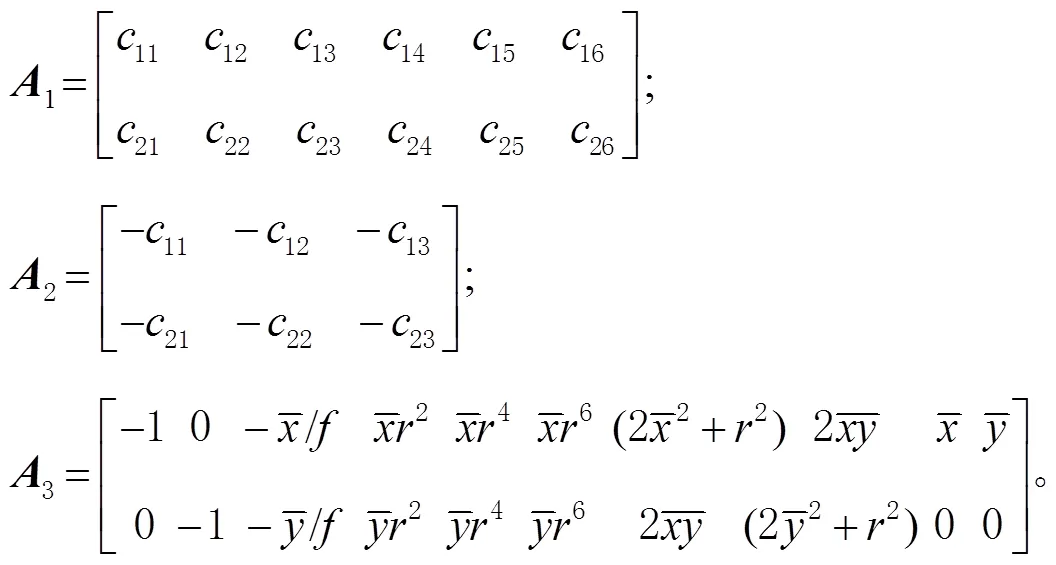
c(=1,2,=1,2,…,6)為線性化后投影矩陣的相機系數，為像點的徑向距離。

式（2）~式（4）統稱為數字攝影相機標定的10參數模型，可根據情況對全部或部分參數進行標定。

1.2 相機標定誤差分析

本文應用的高精度工業相機相機參數如表1所示。

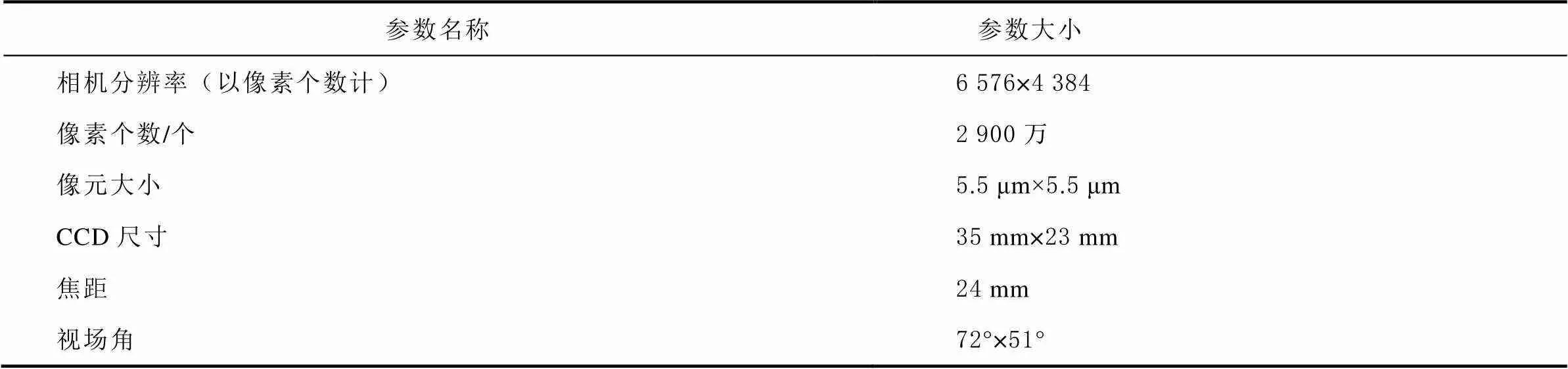
表1 高精度相機參數

標定測量方法是使用高精度單相機，對氣浮臺錐形筒上的編碼標志進行測量而完成的。相機測量精度取決于像點提取的精度、測量物體的大小和測量距離。

2 真北基準、相機與臺體坐標間轉換

為測量獲取氣浮臺裝置在真北基準下的實時姿態角，采用立方鏡光學準直技術、陀螺全站儀定向尋北和同名點坐標系轉換等相結合的方法，通過臺體立方鏡坐標系，完成動態測量相機坐標系和真北基準間關系的建立[11]。

2.1 臺體坐標系與真北基準間的標定

臺體坐標系與真北基準標定工作有2個方面：①通過對臺體立方鏡的準直測量，以及各臺儀器間的互瞄，來建立臺體坐標系；②尋找真北基準，將真北基準引到基準立方鏡上，再通過幾次方位角的轉折傳遞，來標定臺體立方鏡準直面法線的地理方位角。

實驗采用3臺LeicaTM6100A電子經緯儀和1臺陀螺全站儀。為了讓各臺儀器間能夠通視，需要對各臺儀器的安放位置進行調整，實驗室測量情況如圖1（a）所示。利用陀螺全站儀和LeicaTM6100A電子經緯儀間的相互瞄準觀測來解算2立方鏡間的轉角，如圖1（b）所示。

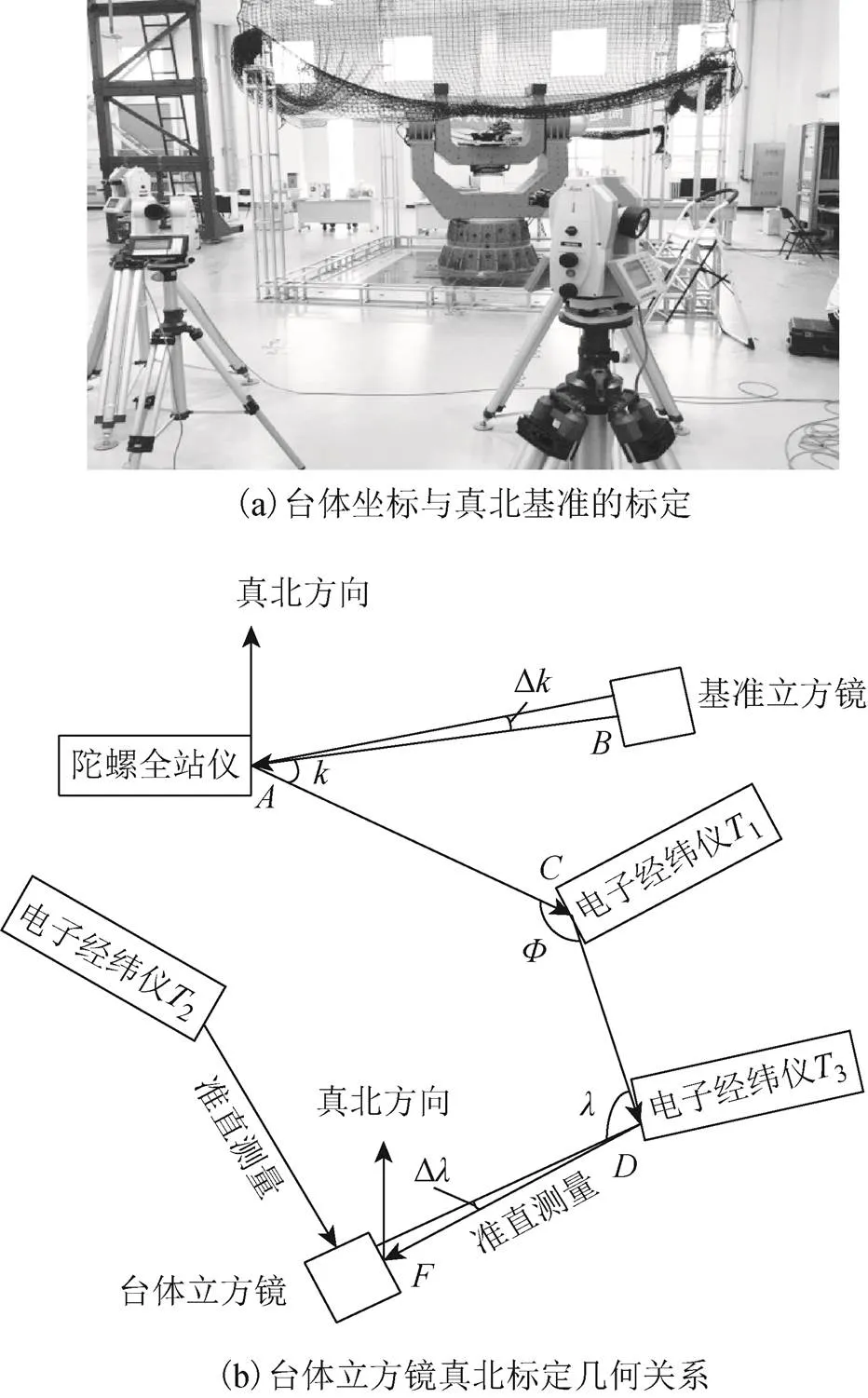
圖1 臺體坐標與真北基準間的標定

首先通過準直測量確定準直面法線方向，采用交會法測定立方鏡中心點坐標；其次由儀器間的互瞄測量，得到各儀器設站位置點的空間坐標；最后得到立方鏡中心點坐標和2臺準直經緯儀所在點的坐標。以立方鏡中心為原點，通過3個點確定臺體立方鏡坐標系的軸和軸，再由右手準則得到軸，最后測出臺體立方鏡準直面法線的地理方位角，即為立方鏡坐標系軸的地理方位角，由此便建立了臺體坐標系與真北基準之間的聯系。

2.2 相機坐標系與臺體坐標系間的標定

相機坐標系與臺體坐標系之間的標定主要通過公共點的轉換來實現。分別使用標定相機和全站儀測量臺體上的標志點，獲取同名標志點在標定相機坐標系和臺體坐標系下的坐標數據，經過計算得到2坐標系之間的轉換參數（如表2所示）。

表2 單相機與標定相機間的轉換參數

由此建立動態測量相機坐標與標定相機坐標、標定相機坐標與臺體坐標之間的轉換關系，又因標定相機坐標系在前后2次轉換中保持不變，故動態測量相機坐標系下的測量成果在經過2次坐標間的轉換后，得到臺體坐標系下的測量值，并且臺體坐標在此之前經過與真北基準之間的標定，最終將臺體坐標系下的值轉換到真北基準下，獲得氣浮臺真北基準下的實時姿態角。

3 實驗與結果分析

3.1 相機標定實驗

將標定板放置在穩定且周圍無其他雜點的位置上，手持待標定相機從標定板正面、正面旋轉90°、前俯、后仰、左傾斜和右傾斜角度進行拍攝；采用攝影測量系統IDPMS進行解算，經掃描、標志點提取、匹配和平差迭代，獲得標志點點云（如圖2所示）。

圖2 4相機標定點云數據

根據上述求解的標志點坐標，采用待標定的10參數模型建立相機內部參數誤差方程式，經解算得到4相機內部參數標定結果（如表3[12]所示）。

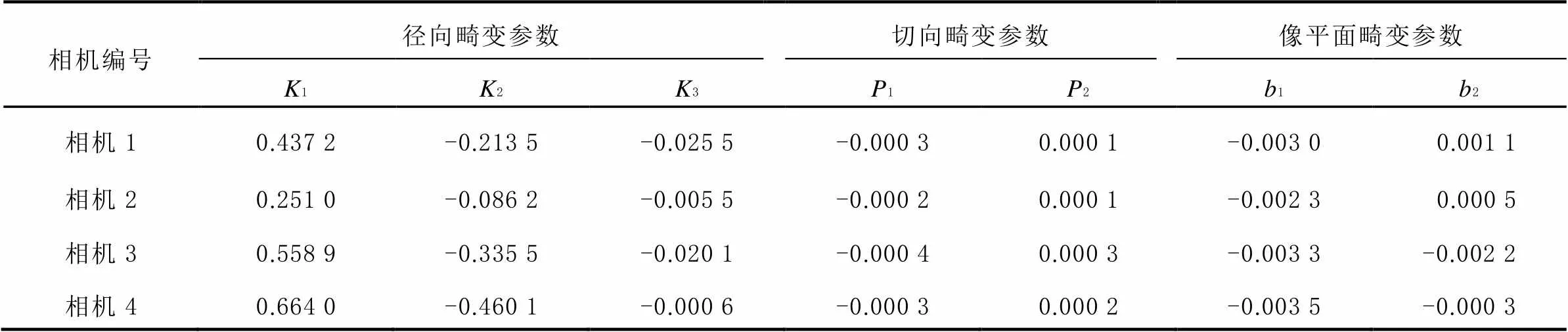
表3 測量相機內部參數標定結果

為體現相機標定對測量結果的影響，設置了7組不同畸變標定參數來進行實驗。將物方點坐標計算值與高精度標定相機測量值進行對比，統計坐標差值，并用均方根（root mean square, RMS）來評定測量點精度，對比結果如表4所示。

從表4可看出：

1）鏡頭光學畸變對測量精度影響較大，相機使用前必須進行標定；

2）3、1和2對坐標測量結果影響較小；

3）采用10參數來修正像點系統誤差是有效的。

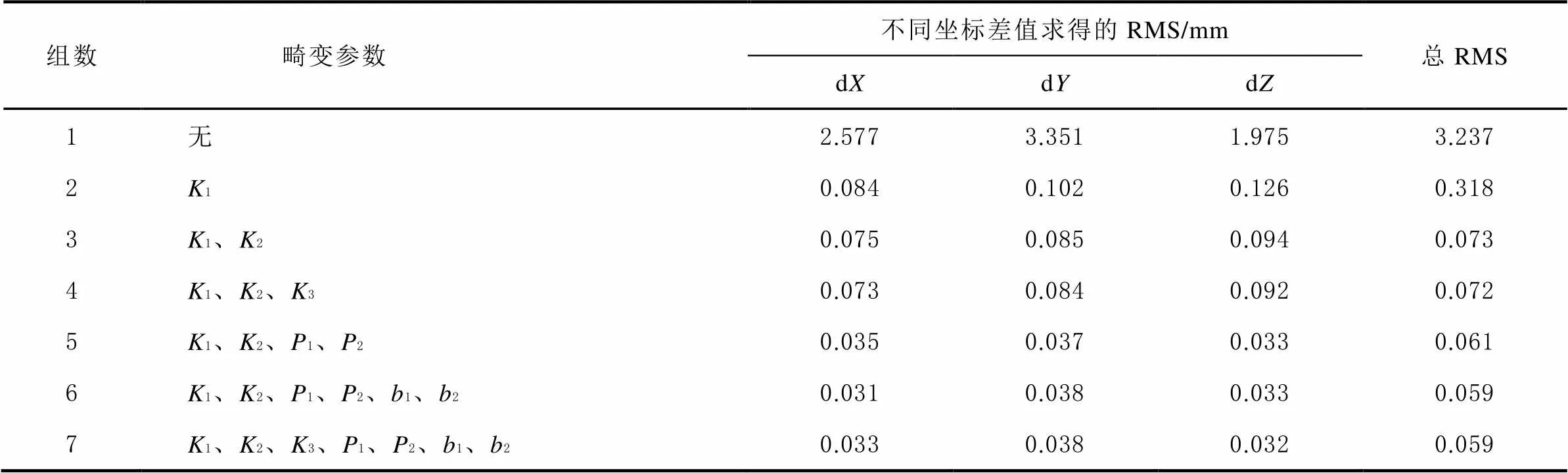
表4 不同畸變參數標定結果

3.2 錐形測量控制網布設

實驗采用模擬現場環境的方式來模擬氣浮臺工作，在相對穩定的環境下，采用錐形構件代替氣浮臺錐形筒，在錐形構件內側粘貼直徑為6 mm的編碼標志塊和無編碼標志點，多個標志塊和多個標志構成了錐形檢定實驗場。錐形筒內編碼標志粘貼情況如圖3(a)所示。首先，利用標定子系統中的高精度標定相機模塊對錐形構件進行拍攝，獲取錐形構件控制場圖像；其次，將圖像導入IDPMS中進行圖像掃描、標志點識別和特征點匹配等處理，經光束法平差迭代得到控制場內各標志點坐標，最后，將其結果作為后續測量數據解算的控制點。經解算得到控制場標志點點云如圖3(b)所示。

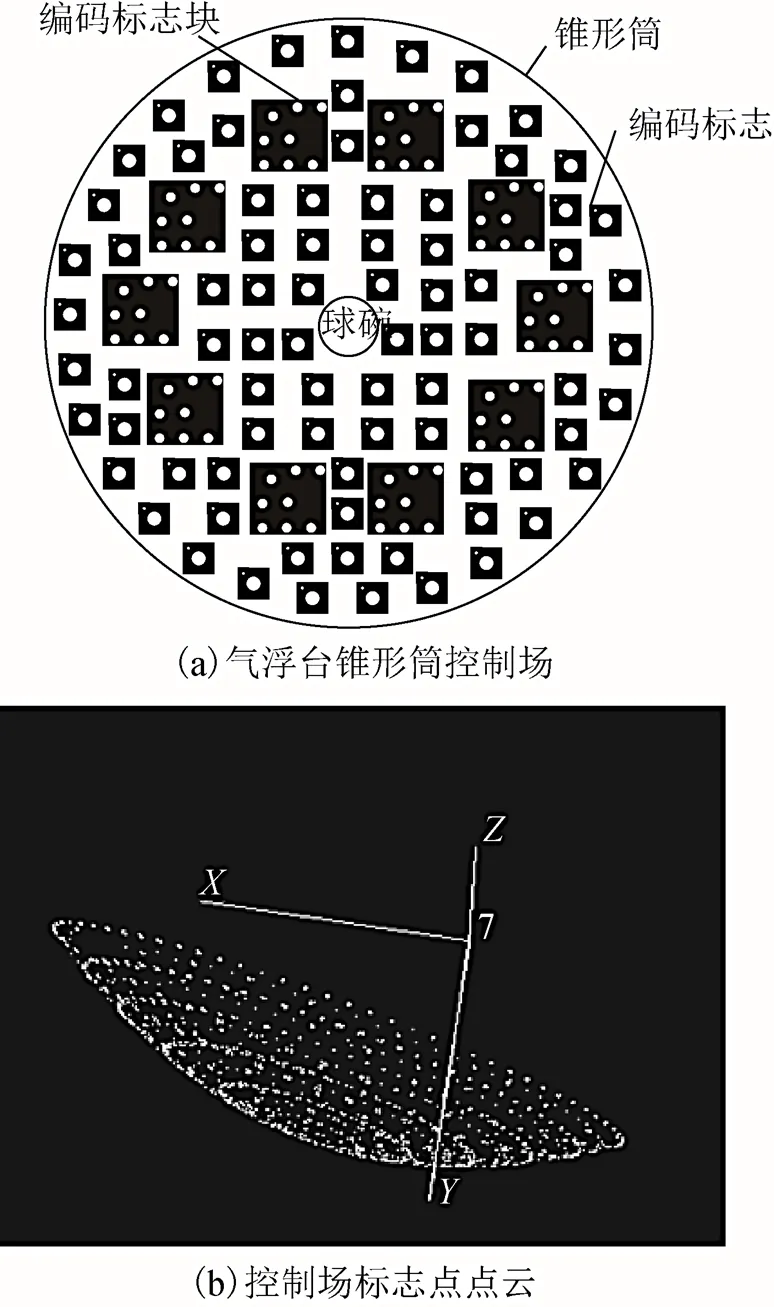
圖3 氣浮臺錐形控制場與標志點點云

3.3 理論測量精度

使用單相機后方交會對氣浮臺實時姿態角測量，設計相機的測量精度小于等于10″，即在單相機后方交會時，測量精度小于等于48.5 μm。測量誤差源來自于相機及解算模型誤差。

采用后方交會進行精度評定的方法為

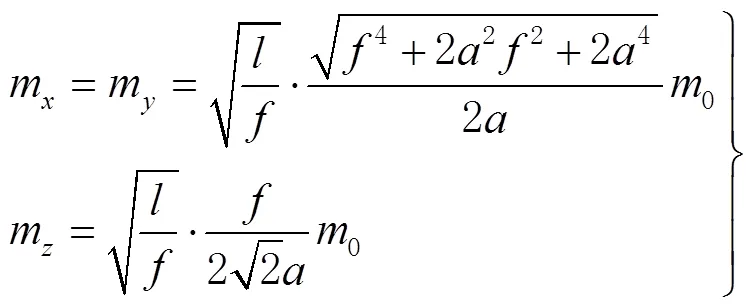
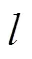
3.4 實驗測量精度

實驗方法為：保持錐形構件垂直朝下的初始位姿，用4臺測量相機豎直向上對準錐形構件靶面；在4臺相機中央架設三角支架，在支架上固定錐形構件。調節支架使構件旋轉1周，轉動過程中4臺相機對構件進行實時拍攝，獲取標志點圖像后進行解算，所得點云數據及4臺相機在控制場中的位置如圖4（a）所示。為驗證這種方法的可靠性[13-14]，采用3 mm的編碼塊和標志點重新布設錐形構件，然后再次測量，得到點云數據如圖4（b）所示。

圖4 相機獲得靶面標志點電云

對標志點坐標數據進行光束法平差，得到測量點的結果如表5所示。

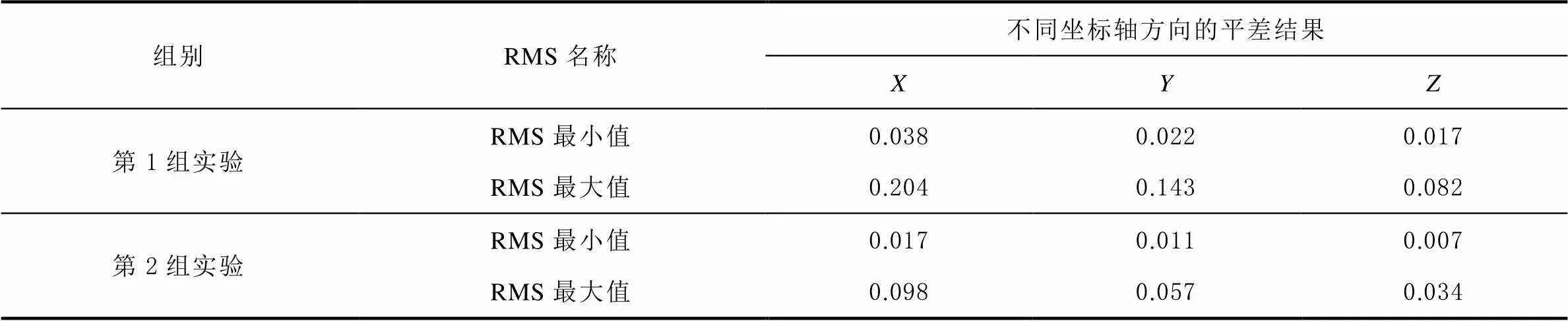
表5 測量點坐標平差結果 單位：mm

從表5可以看出，標志點坐標2次平差結果在、和3個方向上最小偏差分別為0.038、0.022和0.017以及0.017、0.011和0.007mm，相機測量及解算的點位精度高，可作為基準數據，為后續測量值作對比參考。

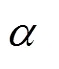
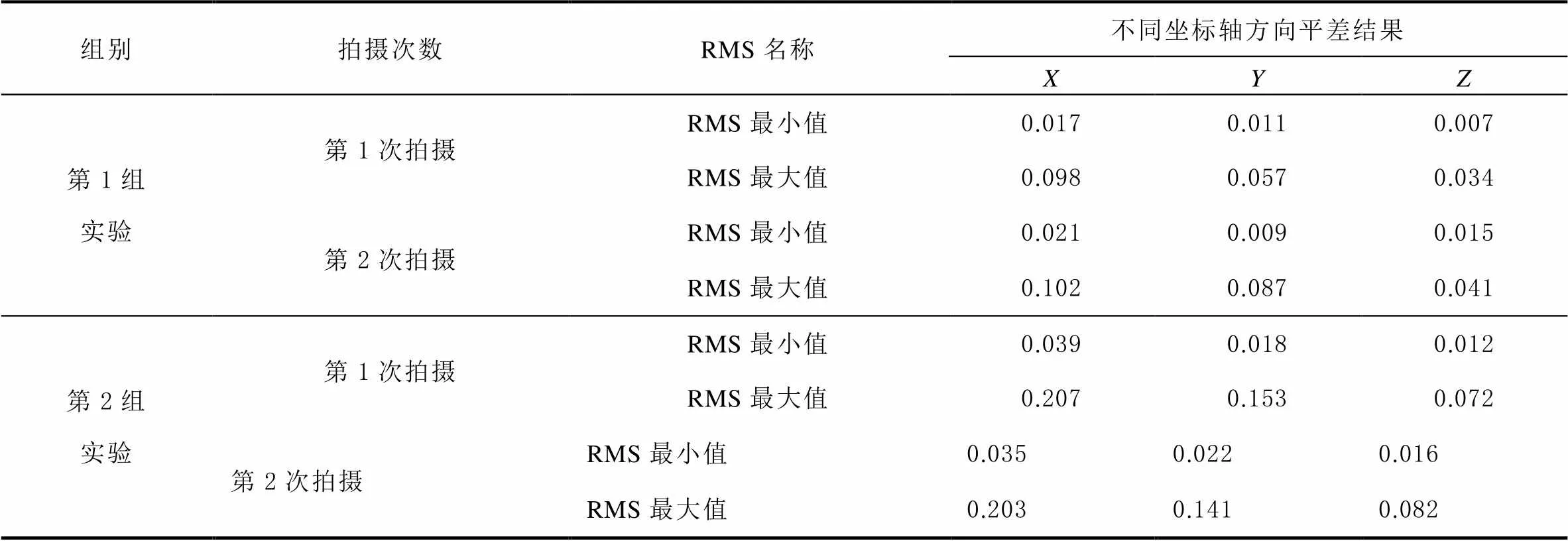
表6 位姿變化后標志點平差結果 單位：mm

根據前后變化的標志點坐標數據，解算模擬構件在3軸方向的角度變化，解算結果如表7所示。

從對準結果的坐標殘差值來看，2次標志點對準效果相當，在3軸方向上的點位對準精度在0.02~0.05mm的理想解算精度范圍，標志點坐標測量結果準確有效。

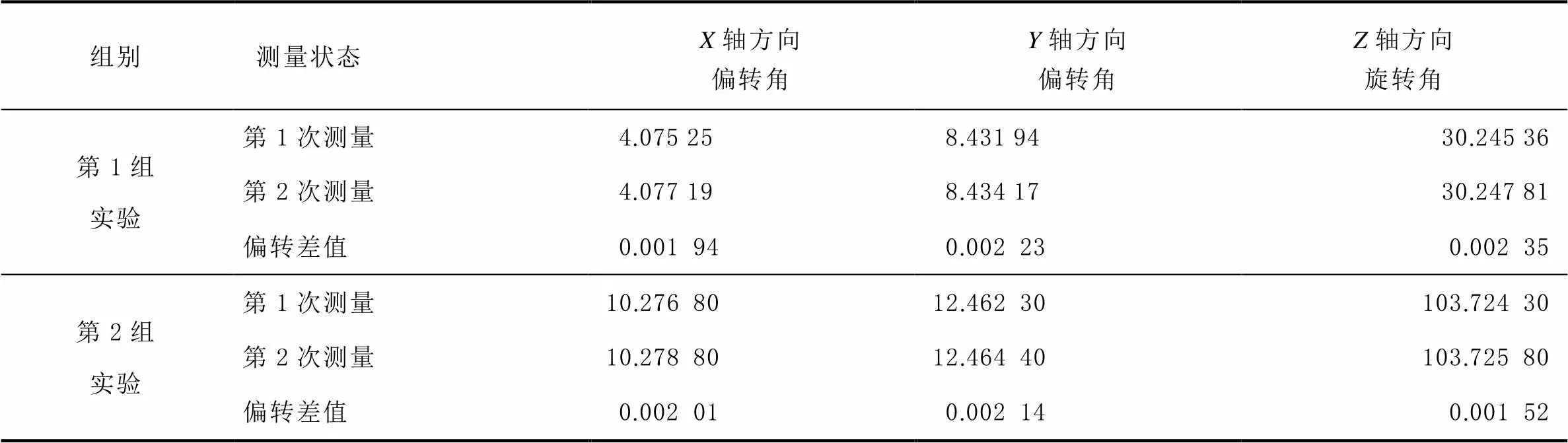
表7 模型相對初始位姿偏轉值 單位：°

第1次實驗測量相機在3軸方向上對模擬構件角度重復測量的誤差分別為0.00194°、0.00223°和0.00235°，即差值為6.984″、8.028″和8.46″，3軸方向角度測量偏差不超過10″，滿足測量精度要求。

第2次實驗測量相機在3軸方向上對模擬構件角度重復測量的誤差分別為0.00201°、0.00214°和0.00152°，即差值為7.236″、7.704″和5.472″，可排除測量精度效果具有的偶然性。說明采用標定的測量相機能夠實現對氣浮臺模擬構件的精確測量，在3軸方向，姿態角的測量誤差不大于10″。

4 結束語

通過分析氣浮平臺姿態測定的任務需求，提出采用近景攝影測量方法對氣浮平臺的位姿進行測量。為獲得可靠的結果，首先利用10參數模型對高精度工業相機進行標定，然后通過標志點坐標解算來獲取氣浮仿真實驗平臺在3軸方向的位姿信息，經對錐形構建的實驗室模擬測量，得出如下結論：

1）鏡頭光學畸變對測量精度影響較大，經過10參數模型標定后的相機在測量誤差精度上要高出1~2個數量級，相機參數標定是必要的。

2）對動態測量相機后方交會的精度進行分析后，總結出3軸氣浮臺姿態角測量方案的理論精度，模擬實驗表明，該測量方案在3軸方向的偏轉重復誤差均小于10″，驗證了該測量方案的可行性。

[1] 林海奇. 三軸氣浮臺質量特性優化設計及其參數辨識方法研究[D]. 哈爾濱: 哈爾濱工業大學, 2018.

[2] 潘俊帆, 康國華, 周瓊峰. 三軸氣浮臺重心自動調整研究[J]. 航天控制, 2017, 35(2): 83-88.

[3] 李新峰, 向東, 田興華, 等. 平面微重力模擬氣浮系統的側向力測量與處理[J]. 系統仿真學報, 2018, 30(10): 3746-3752.

[4] 徐洲洋, 肖東升. 近景攝影測量支持下的地鐵盾構管片姿態測量方法及其應用[J]. 測繪通報, 2019(1): 75-78.

[5] 展浩. 基于MEMS的運動姿態參考系統的設計與研究[D]. 哈爾濱: 哈爾濱工程大學, 2019.

[6] 肖巖, 葉東, 孫兆偉.面向三軸氣浮臺的室內星敏感器定姿方法[J]. 哈爾濱工業大學學報, 2016, 48(10): 51-56.

[7] 邱萬彬, 陸婷婷. 基于計算機視覺的三軸氣浮臺姿態確定[J]. 計算機測量與控制, 2015, 23(2): 554-557.

[8] 王恩友. 基于模型預測控制的氣浮臺運動控制研究[D]. 哈爾濱: 哈爾濱工業大學, 2017.

[9] 劉宇航, 顧營迎, 李昂, 等. 氣浮實驗臺位姿視覺測量方法[J]. 紅外與激光工程, 2017, 46(10): 195-202.

[10] 李召鑫. 基于圖像處理的頭盔空間位置測量[D]. 杭州: 浙江大學, 2012.

[11] 晏磊, 陳瑞, 孫巖標. 極坐標數字攝影測量理論與空間信息坐標體系初探[J]. 測繪學報, 2018, 47(6): 705-721.

[12] 楚萬秀. 近景攝影測量標志點設計及信息處理研究[D]. 上海: 東華大學, 2008.

[13] 梅文勝, 胡帥朋, 李謀思, 等. 基于普通數碼相機的旋轉全景攝影測量方法[J]. 武漢大學學報(信息科學版), 2017, 42(2): 243-249.

[14] 黃桂平. 數字近景工業攝影測量理論、方法與應用[M]. 北京: 科學出版社, 2016.

[15] 單杰. 光束法平差簡史與概要[J]. 武漢大學學報(信息科學版), 2018, 43(12): 1797-1810.

A continuous attitude measurement method of three-axis air bearing platform based on close range photogrammetry

ZHANG Jichao，LAN Wenqi，JIN Zelin，YANG Xiongdan，ZHOU Peixi，LIU Jiancheng

（School of Geomatics, Liaoning Technical University, Fuxin, Liaoning 123000, China）

Aiming at the problem that it is reduced for the available load of the air bearing platform due to the large space occupied by the existing measurement methods in the attitude measurement of the three-axis air bearing simulation experiment platform, the paper proposed a continuous attitude measurement method of the three-axis air bearing platform based on close range photogrammetry: the task requirements of the attitude measurement of air flotation platform were analyzed, and the ten parameter model was used to calibrate the high-precise industrial camera; then the artificial mark points were set up in the air flotation platform, and the measured values under the camera calibration system were converted into the true north datum through the platform coordinate system, so as to complete the construction of the attitude measurement platform of the air flotation simulation device and realize the continuous dynamic measurement of the air flotation platform. Experimental result showed that the repeated measurement errors of the proposed method would be better than the designed 10″ tolerance value in the three-axis direction, which could provide an reference for reducing the development risk of spacecraft systems with its feasibility and effectiveness.

three-axis air bearing platform; close range photogrammetry; calibration; true north datum; attitude angle measurement

P228

A

2095-4999(2020)03-0069-07

張繼超，蘭文琦，金澤林，等. 一種基于近景攝影測量的三軸氣浮臺連續姿態測量方法[J]. 導航定位學報, 2020, 8(3): 69-75.（ZHANG Jichao, LAN Wenqi, JIN Zelin, et al. A continuous attitude measurement method of three-axis air bearing platform based on close range photogrammetry[J]. Journal of Navigation and Positioning, 2020, 8(3): 69-75.）

10.16547/j.cnki.10-1096.20200311.

2019-01-09

張繼超（1975—），男，內蒙古赤峰人，博士，副教授，研究方向為遙感數據處理與應用。

金澤林（1996—），男，遼寧撫順人，碩士研究生，研究方向為近景攝影測量和工程測量。