水輪機混凝土蝸殼液固兩相流的CFD分析

孫 毅，岳曉娜，胡 蝶

(湖南水利水電職業技術學院，長沙 410100)

0 引 言

蝸殼的作用是使水流形成環量，以便水流能均勻、無損能量地分配到轉輪的四周，使水輪機能夠平穩、高效地運行。文獻[1]從理論上分析了蝸殼中水流的運動情況，得到了將蝸殼外形設計成等角螺線的形狀，可使水力損失最小的結論。此時，蝸殼內水流的流動是軸對稱有勢流，流動過程中能量損失最小，其特征是速度矩為常數，即Vur=K。

蝸殼按照制作材料的不同，分為金屬蝸殼和混凝土蝸殼。水頭小于40 m時，可以采用混凝土蝸殼；水頭大于40 m時，應選擇金屬蝸殼。本文主要研究混凝土蝸殼。

關于混凝土蝸殼的設計，衛建新等[2]在1964年提出了采用數解法繪制混凝土蝸殼的方法，該法解決的是在已知進口斷面形狀及尺寸的情況下，如何確定其他中間斷面尺寸的問題。1984年，歐陽建國[3]編制了蝸殼設計與繪圖程序，該程序采用調用編程語言繪圖函數的功能繪制蝸殼的平面圖。1994年，鄧鳳舞[4]對混凝土蝸殼設計的數值解析計算公式進行了推導，編寫了計算機電算程序，所設計的程序可選定混凝土蝸殼型式，同時可得出計算結果，繪出蝸殼單線圖。1998年，陳建國等[5]用Qbasic語言編寫了混凝土蝸殼的設計程序。2014年，姜鋒等[6]對多種混凝土蝸殼的設計方法進行了比較，介紹了一種新的蝸殼設計方法—變速度矩法，并舉例在二灘水電站金屬蝸殼設計中，自蝸殼進口斷面起至200 °范圍內，按等速度矩方法進行設計；在剩余范圍內，為減輕因斷面面積過小而引起的水速過大，按10%遞減速度矩進行設計，加大了這一段蝸殼的斷面面積，避免在蝸殼鼻端形成高速水流造成流態破壞。

綜上所述，利用計算機編程進行蝸殼設計和繪圖，已經取得了大量成果。但上述的繪圖方法，均是調用計算機編程語言本身的繪圖函數進行繪圖。這種方法繪制的圖形，雖然可用于指導工程建設，卻無法被CFD的前處理軟件讀取，因此無法進行進一步的CFD模擬分析。鑒于此，我們開發了混凝土蝸殼計算機設計并調用專業繪圖軟件進行繪圖的方法，編制了計算機程序[7]，調用專業的繪圖軟件繪制混凝土蝸殼的三維立體圖，以便可以方便地被CFD軟件的前處理軟件讀取，從而對所設計的混凝土蝸殼進行CFD分析，評價蝸殼的性能。

本文以設計流量24.5 m3/s的混凝土蝸殼的設計為例，介紹了采用作者開發的混凝土蝸殼設計程序所設計蝸殼的水沙兩相流的CFD分析，結果如下。

1 模型選擇與仿真條件的確定

1.1 兩相流模型的選擇

CFD分析一般是通過求解時均N-S方程來實現的[8]。不同的流動狀態，其N-S方程的形式和處理方法也不同。在Fluent中，對于兩相流，其數學模型有VOF法、混合法、歐拉法和分散相法。其中歐拉法的適用范圍最廣，因此，本文選用歐拉法進行水沙兩相流的分析。

歐拉多相流模型也稱為歐拉-歐拉法。該法原則上可用于任意多相流體的仿真分析，但一般不超過三相。這是因為，當相數過多時，其解不易收斂。該法把多相流的各相看做是互相貫通的，各相所占的比例用體積分數α表示。若多相流中共有n相，則各相的體積分數之和為1，即：

(1)

可通過求出各相的體積分數分布了解各相的分布情況。

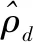
(2)

在fluent中，歐拉多相流模型的壓力是被各相共享的，連續性方程和動量方程是對每一相求解[9]。

對于第q相，其連續性方程為：

(3)

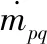
第q相的動量方程為：

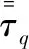
1.2 湍流模型的選擇

進行CFD分析的前提是具有合適的湍流模型。常用的湍流模型有零方程模型、一方程模型和兩方程模型。目前，常用的湍流模型是兩方程k-ε模型，其中20世紀70年代Launder發展的k-ε模型是最基本的k-ε模型，被稱為標準k-ε模型，它的表達式如下[9]：

(5)

(6)

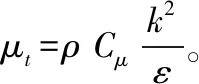
根據文獻記載[10]，在標準k-ε湍流模型下，對蝸殼模擬出的流體流動狀態較好。因此，本文選擇標準k-ε湍流模型作為蝸殼內水沙兩相流CFD分析的湍流模型。

1.3 仿真條件的確定

1.3.1 含沙量

蝸殼工作在天然水流下，水中不可避免含有一定量的泥沙。不同的河流，含沙量不同，以黃河含沙量最高[11]，可達37.5 kg/m3，按沙粒密度2 550 kg/m3[12]計，相當于含沙濃度(體積百分數)為1.47%。據此，本研究含沙濃度的最大值設定為1.5%，取0.5%、1%和1.5% 3個水平。

1.3.2 沙粒粒徑

據報道[13]，河沙的粒徑均在5 mm以下，其中粒徑在1.18 mm以下的占86%。水流經水庫沉淀后，進入水輪機的水流中沙粒的粒徑較小，一般在0.05 mm左右，如扎拉水電站過機泥沙粒徑的中值為0.03 mm[14]。

由上可知，這是一個2因素3水平的模擬實驗，共有9種工況，如表1所示。

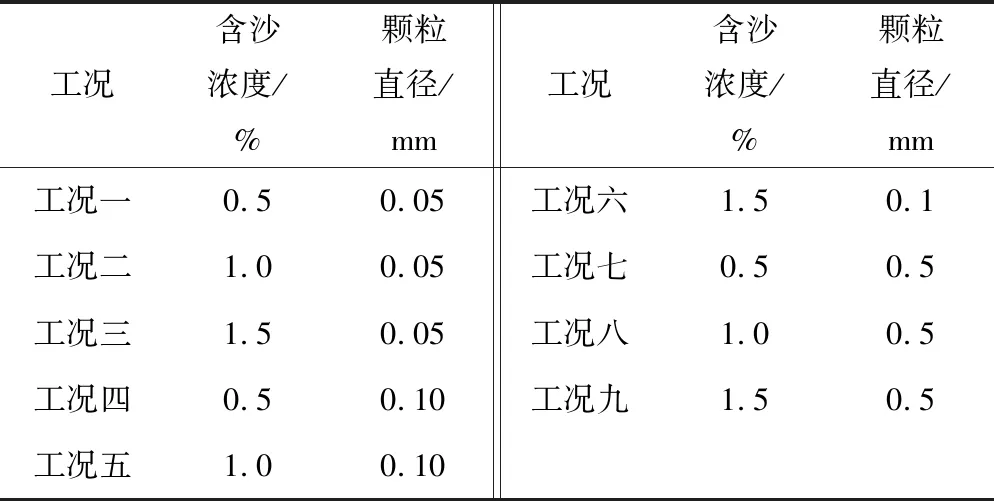
表1 模擬工況Tab.1 Simulated conditions

2 CFD模擬與分析

2.1 蝸殼模型的建立及網格劃分

采用VBA編程方法在AutoCAD中繪制混凝土蝸殼的立體模型[7]。其方法是將設計流量等參數輸入蝸殼設計軟件，得到蝸殼的立體圖，存儲為.sat格式。然后，利用ICEM文件菜單的“Import Model”選項將軟件生成的蝸殼立體圖導入ICEM中進行網格劃分。由于蝸殼形狀復雜，采用非結構化方法、四面體混合網格進行網格劃分。本文所采用的蝸殼進口寬5.9 m，高3.0 m，蝸殼長7.1 m，共劃分為593 076 個網格，如圖1所示。

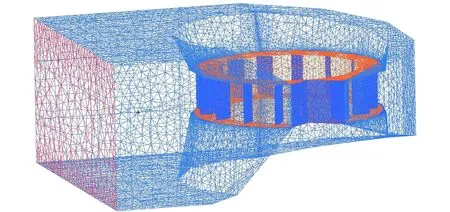
圖1 蝸殼網格劃分Fig.1 Division of the volute grid

2.2 Fluent 計算方法與邊界條件

流體運動遵循物理學3個守恒定律：質量守恒、動量守恒和能量守恒。由于對蝸殼的水沙兩相流分析中，不涉及傳熱問題，故只要考慮質量守恒和動量守恒即可。由于蝸殼內的水流狀態是湍流，所以需要選擇合適的湍流模型。如上所述，選擇標準k-ε湍流模型，近壁面采用標準壁面函數處理。

在本研究中，水和沙均為不可壓縮介質，選擇流速作為入口邊界條件、選擇壓力作為出口邊界條件，選擇Phase Coupled SIMPLE 算法對控制方程求解。

2.3 模擬結果與分析

2.3.1 壓力分布

(1)不同含沙量對蝸殼內壓力的影響。考察相同的沙粒粒徑、不同含沙量時，蝸殼內的壓力，結果見圖2～圖4(以下用d表示粒徑)。

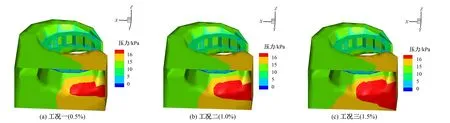
圖2 不同含沙濃度時蝸殼內壓力分布(d=0.05 mm)Fig.2 Pressure distribution in volute at different sand concentrations(d=0.05 mm)

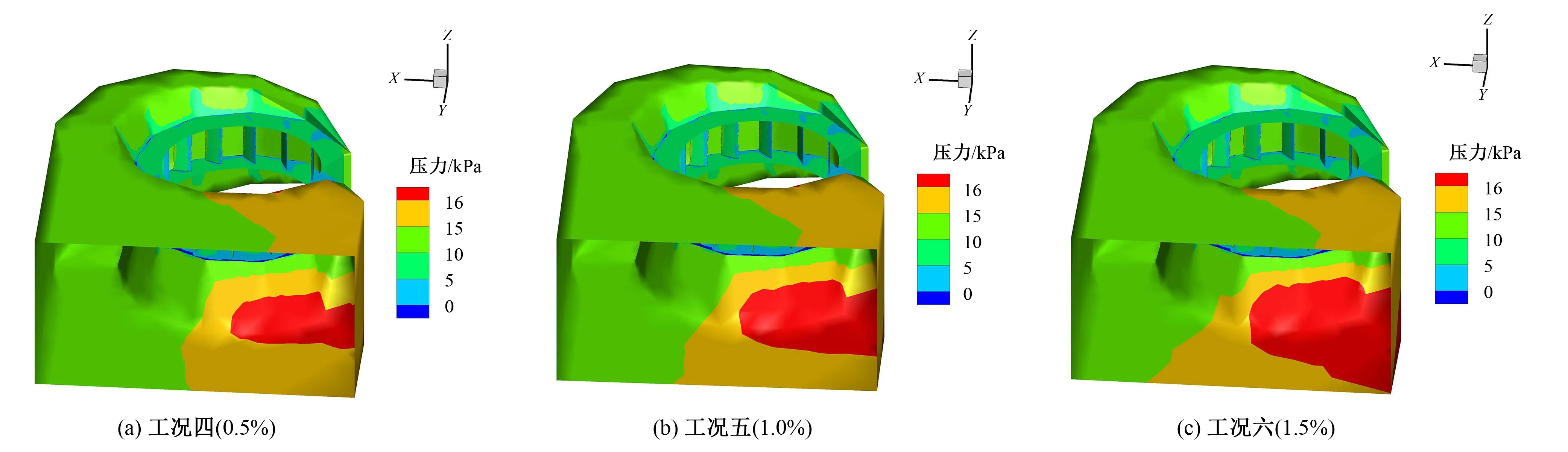
圖3 不同含沙濃度時蝸殼內壓力分布(d=0.1 mm)Fig.3 Pressure distribution in volute at different sand concentrations(d=0.1 mm)

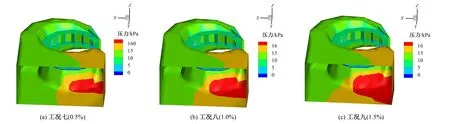
圖4 不同含沙濃度時蝸殼內壓力分布(d=0.5 mm)Fig.4 Pressure distribution in volute at different sand concentrations(d=0.5 mm)

由圖2～4可知，在相同的粒徑下，隨著含沙量的增加，蝸殼內的壓力增加，這是由于沙的密度較大所引起。這提示我們在進行蝸殼設計時，對于含沙量較大的流域進行水電開發時，蝸殼的抗壓強度要提高。從圖中還可以看出，蝸殼內壓力較高的區域，分布在蝸殼的非蝸形部分。這提示我們應對蝸殼的非蝸形部分進行深入的研究。

(2)不同粒徑對壓力的影響。圖2～圖4中的工況一、工況四和工況七的含沙量相同，均為0.5%；工況二、工況五和工況八的含沙量相同，均為1.0%；工況三、工況六和工況九的含沙量相同，均為1.5%。由這三組圖比較可知，當含沙量相同時，不同粒徑對蝸殼內的壓力無明顯影響。

2.3.2 沙粒在蝸殼內的分布

為了考察含沙量和沙粒粒徑對蝸殼內沙粒分布的影響，對不同粒徑、不同含沙量的工況下蝸殼內沙粒體積分數的分布進行了數值模擬，結果如下。

(1)粒徑對沙粒體積分數的影響。對相同含沙量、不同粒徑的沙粒進行數值模擬，結果見圖5～圖7。

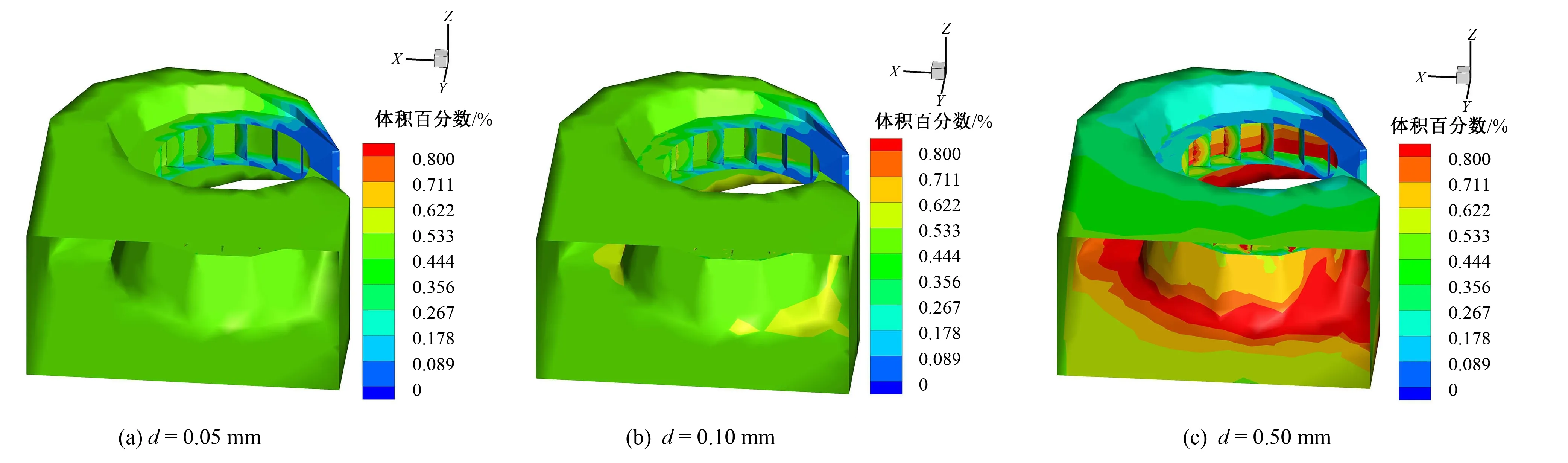
圖5 含沙0.5%時不同粒徑的體積分數分布Fig.5 Volume fraction distribution of different particle sizes at 0.5 % sand content

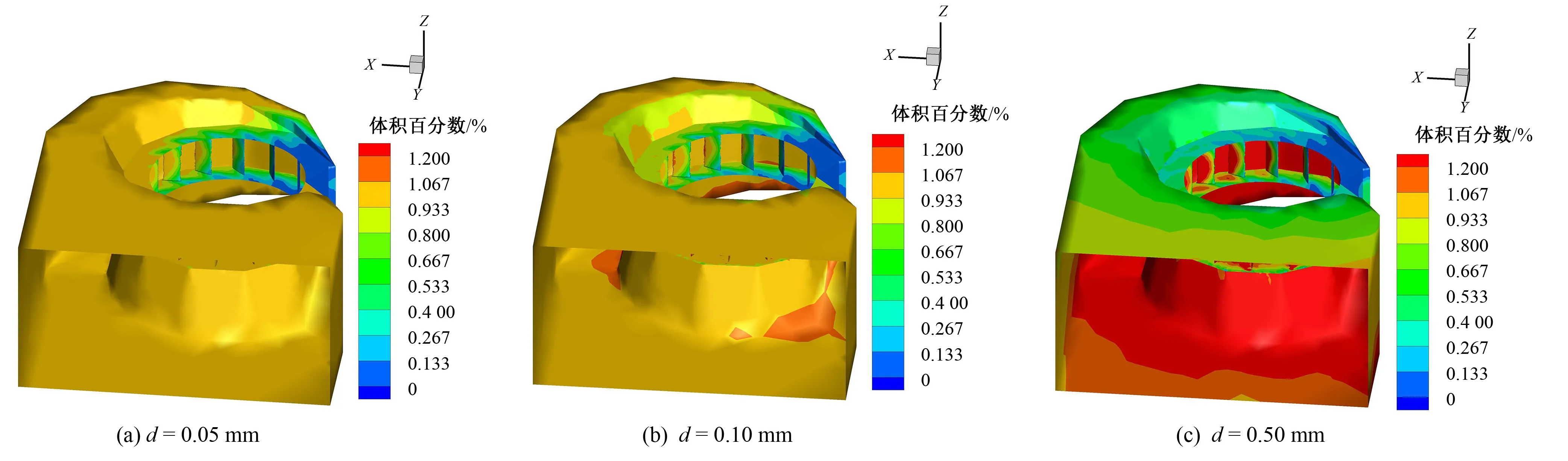
圖6 含沙1.0%時不同粒徑的體積分數分布Fig.6 Volume fraction distribution of different particle sizes at 1.0% sand content

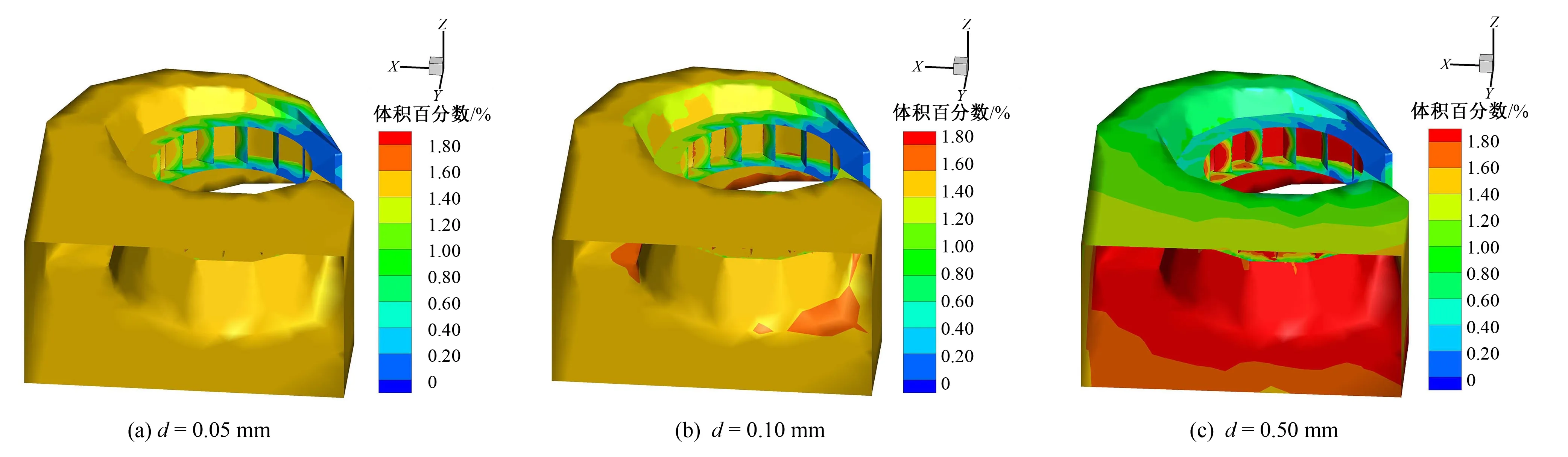
圖7 含沙1.5%時不同粒徑的體積分數分布Fig.7 Volume fraction distribution of different particle sizes at 1.5% sand content

由圖5、圖6和圖7可見，含沙量相同時，隨著顆粒直徑的增加，蝸殼中沙粒的體積分數增加，且底部高于頂部。這是由于含沙量相同時，單個顆粒的直徑越大，整個沙粒的總表面積就越小，沙粒與水之間的相互作用力減弱，重力的作用相對增加，使重力引起的沉降作用更加明顯。

(2)蝸殼進口含沙量變化對蝸殼內沙粒體積分數的影響。為考察蝸殼進口含沙量變化對蝸殼內沙粒體積分數的影響，固定沙粒粒徑，對不同含沙量情況下的蝸殼內沙粒體積分數進行對比，即把圖5～圖7中相同粒徑的圖進行坐標等值處理，以便于觀察。結果如見圖8～圖10。

由圖8～圖10可知，粒徑相同時，隨著蝸殼進口含沙量的增加，蝸殼內的含沙量也越高。

3 結 語

通過對設計流量下蝸殼內液固兩相流數值模擬，可以得到如下結論。

(1)不同含沙量下，含沙量越高，蝸殼內部壓力越高。這提示我們在進行蝸殼設計時，對于含沙量較大的流域進行水電開發時，蝸殼的抗壓強度要提高。

(2)蝸殼內壓力較高的區域，分布在蝸殼的非蝸形部分。這說明，在進行蝸殼設計時，不但要注重蝸形部分的設計，對非蝸形部分的研究也要加強。

(3)含沙量相同時，沙粒在蝸殼內的體積分數隨粒徑增大而增加。這是由于含沙量相同時，單個顆粒的直徑越大，整個沙粒的總表面積就越小，沙粒與水之間的相互作用力減弱，重力的作用相對增加，使重力引起的沉降作用更加明顯。

□