基于神經網絡的精神分裂fMRI數據分類

黃慶坤 楊鵬

(大理護理職業學院 云南省大理市 671000)

大腦作為人體最高級神經控制中樞，一直以來都是神經科學、醫學和生物信息學領域研究人員的研究熱點。功能磁共振成像技術(Functional Magnetic Resonance Imaging，fMRI)憑借高效無創等特性，可用于解讀大腦的工作機理以及判別各種腦相關的潛在患病機制。因此怎樣分析fMRI數據，選取合適的分類特征構建分類器，成為了fMRI數據分類的關鍵。Osmar等人[1]在醫學圖像的檢測中使用了聚類方法從此提出fMRI數據分類的概念，在對于精神分裂fMRI的研究中，Fan等人[2]通過主成分分析法(PCA)和支持向量機(SVM)分類原理對精神分裂fMRI進行數據分類，提出精神分裂患病機制可能由于潛在的腦結構和腦結構的異常所導致；Firat等人[3]在深度網絡中使用到了一種自稀疏編碼的方法，來對大腦的認知狀態進行解碼。

從前人的研究工作來看，對于高維fMRI數據研究采用了特征提取與分類算法相結合的思路，因此存在著特征提取與算法擇優的問題。傳統機器學習大多都為淺層模型,并且對高維fMRI數據存在著不能有效提取特征的問題,并且需要對一般的分類算法進行優化改進。本文結合精神分裂fMRI數據集，在大腦內通過字典學習與區域提取算法劃分感興趣區域，并提取時間序列通過皮爾遜相關系數進行相關性分析，通過特征降維結合神經網絡算法進行分類研究，從腦功能連接的角度出發，更好的輔助臨床診斷。

1 相關方法

1.1 皮爾遜相關系數

皮爾遜相關系數由英國數學家Pearson提出，用于計算變量之間的線性相關程度，對于多維隨機變量，兩兩維度的皮爾遜相關系數p(xi,xj)可描述為：

其中，σ(xi)和σ(xj)分別為xi和xj之間的標準差，cov(xi,xj)為xi和xj之間的協方差，其中cov(xi,xj)可描述為：

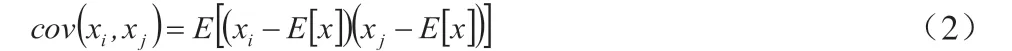
在（2）式中，變量xi和xj之間的相關性與協方差的絕對值成正比，可等價寫作：

其中，P(xi,xj)∈(-1,1)。從（3）式中，我們可以看到xi和xj兩個變量之間的線性相關性越強，其值越接近-1（負相關）或越接近1（正相關），越接近0則相關性越弱，因此皮爾遜相關系數可用于多維隨機變量的相關性分析。

1.2 神經網絡分類模型

在N個樣本數據集N={(x1,y1),(x2,y2),…,(xn,yn) },xi,yi∈R，其中x1,…xn為樣本的n個特征維度，y1,…yn為樣本的實值向量，神經網絡模型通過訓練feature(x1…xn)來獲得label(y1…yn)。假設表示第L層的第j個神經元輸入，為第L層第p個神經元的輸出，表示第L層第i個神經元與第L+1層第j個神經元的權重，表示第L層第i個神經元的偏置值。通過輸入層的值，可以計算隱藏層與輸出層的值：

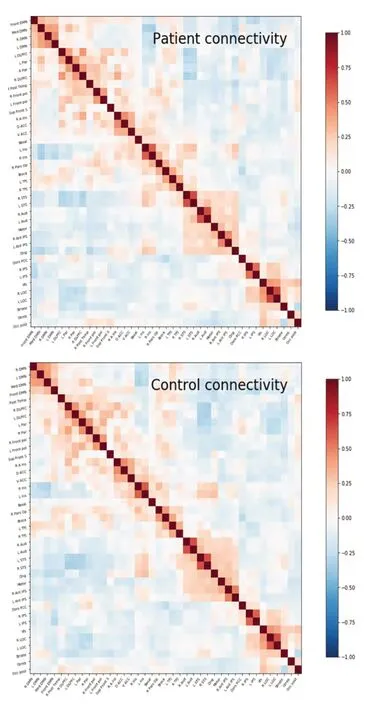
圖1

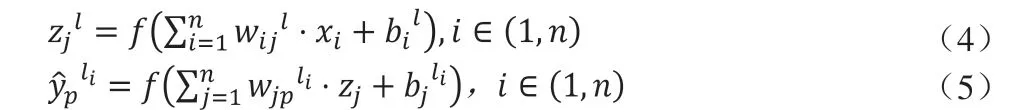
通過梯度下降算法，模型訓練讓樣本的輸入值接近真實值，即E→0。對權值與偏置進行學習，求出各層更新量

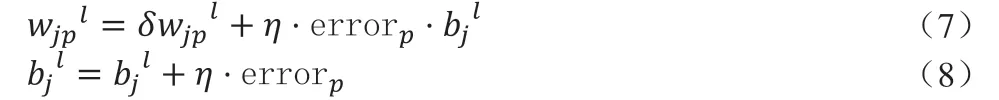
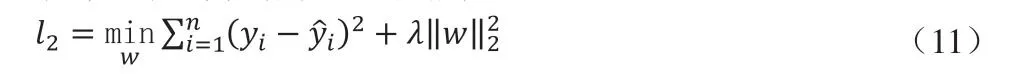
其中，λ>0，為L2正則化參數通過。確定λ的值可以使得在方差和偏差之間達到平衡，隨著λ的增大，模型方差減小而偏差增大。

2 實驗及結果分析

2.1 數據及預處理

Cobre數據集是(The Center for Biomedical Research Excellence,COBRE)為72名被診斷患有精神分裂癥和74名健康對照提供原始解剖和功能性MR數據，每個受試者的fMRI數據集是單個nifti文件（.nii.gz）,FOV=240mm×240mm,slices thickness =3.5mm,plan size= 64×64,voxel size=3.75mm×3.75mm× 4.55mm)。在cobre數據集中，我們首先通過spm8工具包對cobre腦影像數據進行預處理，經過頭動校正、時間校正、標準化、并采用高斯核的全寬半高FWHM=8來對圖形進行平滑化處理。

2.2 特征分類

實驗采用多學科字典學習與區域提取算法得到Atlas腦分區模板[4]，將大腦區域劃分為39個感興趣區域（ROI）。在146個被試中提取39個ROI的時間序列得到一維時間和一維特征矩陣。提取ROI的時間序列后，我們計算每個ROI之間的功能網絡連接性的皮爾遜相關系數，并進行Fisher-Z變換得到相關系數矩陣，來量化大腦不同腦區之間的連接強度。在此基礎上，我們通過PCA降維方法對其進行特征提取，并構建神經網絡分類器，在實驗中，通過交叉驗證后分類準確率如表1。

從表中,我們可以看到在兩個含有隱藏層的神經網絡中對于測試集分類準確率為76.3%，優于文獻[5]的準確率65%和文獻[6]的準確率70.5%，并且對比其他算法的分類效果除了在多個隱藏層節點下無法較好對樣本集較好預測(分類準確率不足60%)外,其他分類算法可較好的完成分類任務，即使在隨機確定參數的情況下，效果也比其好很多。

2.3 結果分析

提取參與訓練的精神分裂癥患者和正常被試的分類腦區特征，并通過皮爾遜相關系數構建相關系數矩陣，如圖1所示。

圖1中橫縱坐標分別代表39個ROI的名稱，對應坐標值為腦區之間的相關性，皮爾遜相關系數值接近在顏色柱兩端，代表特征之間的相關性越強,淺色區域皮爾遜相關系數值為0，代表特征之間不相關，特別地對角線元素值為1，在一些ROI區域之間連接強度存在差異，這些區域主要集中在雙側小腦下葉、顳下回、殼核、尾狀核和海馬旁回等部位，另外在精神分裂癥患者中，枕葉和小腦的有向連接相比正常人的連接更強。同時，枕葉和小腦之間的因果連接在患者中也更強。基于分類特征，我們分析相關性矩陣的平均加權聚類系數、平均特征路徑長度以及平均全局效率，發現精神分裂患者具有較低的聚類系數和全局效率，但是精神分裂患者相對于正常被試特征路徑長度更長，因此精神分裂患者腦網絡節點的集團化程度較低，腦區之間的信息傳輸速率要低于正常被試者。

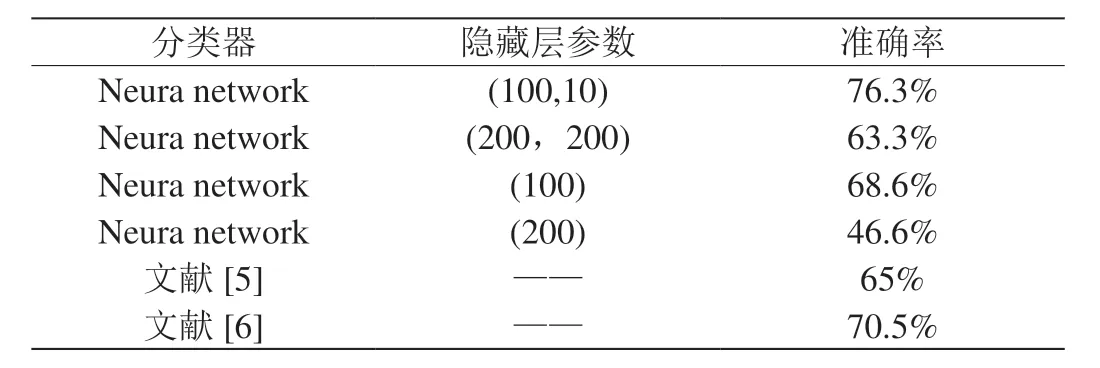
表1

3 總結

本文從數據分類的角度使用了一種基于神經網絡的fMR圖像分類方法，以精神分裂患者與正常被試的腦網絡連接差異性作為分類特征本，并從差異性腦網絡機制的角度去分析潛在患病機制。由于實驗所提出的模型，其用于模型訓練的體素都依賴于先驗知識所劃分的ROI區域，未充分考慮在全腦體素中，是否包含存在其他體素值影響分類的結果，因此下一步將深入了解臨床醫學、腦認知科學相關的專業知識，并與專業人員進行探討，對fMRI數據中非ROI中體素運用到分類模型中，更深層次挖掘信息。