大型機械部件傳動空心軸用液壓聯(lián)軸器內(nèi)外套壁厚設計的研究*

左繼紅 劉麗麗 蔡 頌 崔建波

（1.湖南鐵道職業(yè)技術(shù)學院機車車輛學院 株洲 412001）（2.湖南工業(yè)大學機械工程學院 株洲 412001）

1 引言

聯(lián)軸器廣泛應用在大型機械部件的連接中，傳統(tǒng)聯(lián)軸器與軸連接一般軸上開鍵槽用鍵連接及銷連接，這樣嚴重削弱了軸的最大承載能力及材料的屈服應力；而且大型聯(lián)軸器與軸用鍵連接拆裝時采用壓力機強行冷壓和熱套，會造成軸拉毛損壞從而影響設備的正常工作；液壓聯(lián)軸器的使用很好地解決了這樣的問題，液壓聯(lián)軸器是屬于無鍵連接，主要依靠摩擦力傳遞動力對軸基本沒什么損傷；特別在大型輪船的傳動部件中，液壓聯(lián)軸器廣泛應用［1～7］。

2 大型機械部件空心軸的液壓聯(lián)軸器帶來的問題

現(xiàn)在大型機械部件的傳動軸用液壓聯(lián)軸器一般實心軸，這樣傳遞力矩很大，這樣在設計軸的直徑過程中需要軸的直徑很大，但是由公式：

（其中：ρ為金屬的密度，r為軸的半徑，l為軸的長度。）可知軸的質(zhì)量與軸的半徑的平方成正比，這樣一方面用實心軸會增加軸的總質(zhì)量，不但在傳動中增加了系統(tǒng)的傳動慣性，而且在傳動過程中會增加系統(tǒng)的傳動功率；另一方面軸徑比較大的軸，靠近軸內(nèi)部中心線的地方幾乎不受力，造成大量材料浪費。本研究主要用空心軸代替實心軸來解決實心軸的質(zhì)量過大及出現(xiàn)傳動慣性的問題，同時采用空心軸可以減輕系統(tǒng)的傳動功率計節(jié)省所需材料［7～10］。

實心軸剛度較大，聯(lián)軸器裝配時造成徑向變形量比較小且軸向變形分布均勻，所以聯(lián)軸器內(nèi)外套徑向受力也分布均勻，可以認為徑向變形量和內(nèi)套的徑向受力為常量，這樣可以根據(jù)徑向變形量和內(nèi)套的徑向受力來直接設計聯(lián)軸器的內(nèi)、外套壁厚；但是用空心軸時徑向變形量較大且軸向變形分布不均，聯(lián)軸器內(nèi)外套徑向受力分布也不均。所以設計液壓聯(lián)軸器時無法準確設計內(nèi)、外套的壁厚。這樣必須找出聯(lián)軸器內(nèi)套內(nèi)側(cè)壓力p 在軸向p=f(z) 的變化規(guī)律及壓力與對應徑向變形位移的比值p d，沿軸向的變化規(guī)律p/d=f(z)。這樣才能改變聯(lián)軸器的內(nèi)、外套壁厚，用來安全指導生產(chǎn)［11～16］。

3 船用空心軸的液壓聯(lián)軸器內(nèi)套受力變化規(guī)律分析

聯(lián)軸器內(nèi)套內(nèi)側(cè)壓力與空心軸外徑外側(cè)壓力大小一樣，即空心軸外徑外側(cè)壓力等同空心軸外徑外側(cè)壓力p在軸向的變化規(guī)律［17］。

3.1 受力模型分析

本文選取某家船舶有限公司代號XCF280液壓聯(lián)軸器分析，取一根軸，對這根軸進行分析（圖1 為空心軸和內(nèi)套的液壓聯(lián)軸器受力圖，圖2 為空心軸和內(nèi)套的液壓聯(lián)軸器的剖面圖）。由圖可知空心軸直徑之比dc/da=0.3，液壓聯(lián)軸器內(nèi)套與空心軸配合的外表面錐度為1∶80。

圖1 空心軸和內(nèi)套的液壓聯(lián)軸器受力圖

圖2 空心軸和液壓聯(lián)軸器的內(nèi)套的剖面圖

由圖可知液壓聯(lián)軸器內(nèi)套與空心軸配合的外表面錐度很小，所以裝配后液壓聯(lián)軸器內(nèi)套主要承受液壓聯(lián)軸器外套收縮的徑向力和軸向力可以忽略不計，用Pro/MECHANICA 對圖1 所示的均布p=40MPa 的壓力（相當于外套的徑向壓力）進行分析（圖3 為空心軸和液壓聯(lián)軸器的內(nèi)套受力及變形圖）。

圖3 空心軸和液壓聯(lián)軸器的內(nèi)套受力及變形圖

圖4 為空心軸外側(cè)所受液壓聯(lián)軸器的內(nèi)套的壓力，圖5位空心軸外徑的變形位移，表1是數(shù)據(jù)采集表（z為沿軸向內(nèi)套所在位置為787mm～1200mm、空心軸外側(cè)所受液壓聯(lián)軸器的內(nèi)套的壓力p、空心軸外徑的變形位移d、空心軸外側(cè)所受液壓聯(lián)軸器的內(nèi)套的壓力與空心軸外徑的變形位移比值p/d）。

圖4 空心軸外側(cè)所受液壓聯(lián)軸器的內(nèi)套的壓力曲線

圖5 空心軸外徑的變形位移曲線

表1 數(shù)據(jù)采集表

3.2 空心軸外側(cè)所受液壓聯(lián)軸器的內(nèi)套的壓力變化規(guī)律

本文用SAS 軟件來分析表1 所示空心軸外側(cè)所受液壓聯(lián)軸器的內(nèi)套的壓力回歸曲線（如圖6）。

圖6 液壓聯(lián)軸器的內(nèi)套的壓力樣條法去平滑噪音數(shù)據(jù)的回歸曲線（700＜z＜1200）

由圖4 及圖6 回歸曲線圖可知在，內(nèi)套主要裝配在 787mm 以后，所以 z＜700 沒有研究意義；最后一段（900＜z＜1200）回歸線顯示在水平線壓力值（42＜p ＜44 MPa）間上下波動，可以認為壓力比較穩(wěn)定；變化比較大的是在（700＜z＜900）壓力值（4＜ p ＜42 MPa），特別是裝配內(nèi)套最左側(cè)變化特別大。

本文主要研究z＞700 是找出內(nèi)套的壓力p 與軸向位置z 的方程p=f(z)，經(jīng)過回歸曲線圖分析，符合高斯曲線的特征；本文用建立SAS軟件來分析壓力的回歸曲線的建立高斯曲線的數(shù)學模型方程如下：

（x為軸向位移z，y為液壓聯(lián)軸器的內(nèi)套的壓力p）

分析圖4 空心軸外側(cè)所受液壓聯(lián)軸器的內(nèi)套的壓力曲線，在圖中取2 組數(shù)據(jù)：所以第一組數(shù)據(jù)為（0，0）（z=0，p=1，為計算方便，x=z=0；坐標上移p=0，這樣 y=p=1）；第二組數(shù)據(jù)為（+∞，44）（900＜z＜1200 回歸線顯示在水平線壓力值（42＜ p ＜44 MPa）間上下波動，可以認為壓力比較穩(wěn)定，曲線接近水平線，當x=+∞，取10 個數(shù)據(jù)平均，可以認為y=p=44.06007194。

將以上兩組數(shù)據(jù)帶入式（1）：

解上式可得：a=b=44.06007194，即式（1）為

式（2）整理變形后可得：

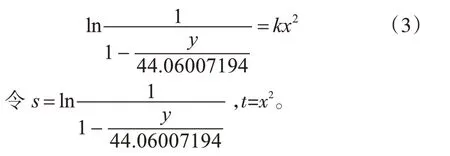
將式（2）中壓力p和x的數(shù)值對應輸入到式（3）的 y 和 x，把 s 作為因變量，t 作為自變量，用 SAS 軟件進行線性回歸分析后可得：

即式（3）中k=0.0000071。

將式（4）帶入到式（2），可得壓力方程：

注：常數(shù)項2.92076是對方程模型的修正。

從表可以看出用式（6）計算得到的理論y 值與實際壓力p 值相比數(shù)據(jù)大小相差不大，所以經(jīng)過曲線和高斯公式計算的方程是可靠的，可以根據(jù)把理論y 值當成空心軸外側(cè)所受液壓聯(lián)軸器的內(nèi)套的壓力，用來計算生產(chǎn)聯(lián)軸器的內(nèi)套內(nèi)套壁厚。

3.3 空心軸外側(cè)壓力與對應徑向變形位移規(guī)律

用SAS 軟件分析表1 中p/d 值，可以計算出p/d的回歸曲線，見圖7。

圖7 空心軸p/d的比值樣條法平滑噪音數(shù)據(jù)的回歸曲線（700＜x＜1200）

由圖分析可知p/d 出現(xiàn)不規(guī)律的線性下降，用SAS軟件對p/d的比值進行現(xiàn)行和回歸計算可得：

圖8 空心軸p/d的比值的二次回歸曲線（700＜x＜1200）

圖8 為空心軸p/d 的比值的二次回歸曲線，分析可知回歸效果較好，比較準確地反映了空心軸外側(cè)壓力與徑向變形位移比值的變化發(fā)展趨勢。

4 結(jié)語

本文設計的船用空心軸在保證傳動不發(fā)生變化情況下可以減輕傳動軸重量及傳動慣性，經(jīng)過對液壓聯(lián)軸器內(nèi)套內(nèi)壓力p 沿軸向的變化規(guī)律p=f(z) 分析研究得出了一個p=f1(x)=44.06007194·(1-e-0.0000071x2+2.92076)，理論壓力值與實際壓力p 值基本相同。空心軸外側(cè)壓力與徑向變形位移比值的變化發(fā)展趨勢分析回歸方程實際效果良好，可以用來指導生產(chǎn)，為液壓聯(lián)軸器的內(nèi)、外套壁厚設計提供理論支撐。