超/高超聲速飛行器動態穩定性導數極快速預測方法

李正洲，高昌，肖天航，馬自成，肖濟良，朱建輝

1. 中國空氣動力研究與發展中心 高超聲速沖壓發動機技術重點實驗室，綿陽 621000

2. 南京航空航天大學 航空學院，南京 210016

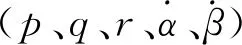
目前獲取動導數的主要方法有飛行試驗、風洞試驗[4-5]、數值計算[6-10]及工程近似方法等。飛行試驗和風洞試驗是飛行器動態特性判定的主要依據，但存在難度大、周期長、費用高的特點，需要與數值計算相互補充、互相驗證；采用非定常CFD數值模擬方法，可以考慮到流場的非線性特性，便于開展復雜外形的氣動力計算，但主要局限性在于計算量大，難以快速獲得定性的結論和定量判據；以牛頓撞擊理論[11]為代表的工程近似法考慮了線化空氣動力學理論和經驗關系，具有快捷高效的優勢，但對復雜外形的大迎角非線性流動可能在數值上存在量級甚至符號的差別。

動導數的高效預測關鍵在于飛行器非定常氣動力的快速、準確計算。在非定常氣動力快速計算方面，近年來的熱門方向是降階模型(Reduced Order Modeling, ROM)[12]，這一方法在計算精度和計算效率上取得了很好的平衡。但由于降階模型仍然部分依賴耦合非定常CFD數值計算，對非定常數值求解的魯棒性有較高要求，因此一些學者轉而采用定常CFD和工程方法相結合的思路構建非定常氣動力模型，其中最典型的是基于CFD技術的當地流活塞理論(Local Piston Theory, LPT)[13]。陳勁松和曹軍[14]、張偉偉[15-16]等基于定常歐拉(Euler)方程計算流場，利用獲得的物面當地流動參數結合活塞理論來計算非定常氣動力，這一方法解決了活塞理論只能計算一定馬赫數范圍內小迎角、尖頭薄翼的缺點；劉溢浪[17]、秦之軒[18]等成功地將該方法應用于氣動導數快速預測。

結合定常CFD與當地流活塞理論的方法來預測動導數，從結果來看，能夠較好地揭示超聲速/高超聲速流動下飛行器動導數的變化規律，相比于完全非定常CFD時域推進方法可以節約大量計算時間。然而，該方法仍然依賴定常CFD流場數據，無法在飛行器設計早期階段快速地給出定性的結果。本文針對上述問題，發展了一種結合當地表面斜度法和當地流活塞理論的高速飛行器非定常氣動力快速計算方法，再對非定常氣動力進行提取、辨識，可得到動導數。該方法不依賴CFD流場結果，在預測動導數方面具有極高的效率，同時具有較高的精度。

1 動導數高效預測策略及流程

本文動導數高效預測策略及流程如圖1所示：① 所需輸入為飛行器物面網格、來流參數及物面隨時間的變形、振動歷程；② 飛行器的非定常氣動力根據當地流活塞理論分為為受自由來流引起的無附加擾動項以及飛行器物面變形或運動引起的附加擾動項；③ 采用基于牛頓撞擊理論的當地表面斜度法求出氣動力無附加擾動項，再根據激波后的等熵關系求解當地流動參數，結合物面變形或振動可求出當地物面下洗速度，繼而求出氣動力附加擾動項隨時間變化；④ 對氣動力無附加擾動項和擾動項沿物面積分，即可求出高速飛行器受到的非定常氣動力。圖中：Ma、H、α、β分別馬赫數、高度、迎角、側滑角；Vl、Vb為飛行器物面的當地速度矢量；α0、αm、k、t分別為強迫旋轉運動的初始迎角、迎角振幅、縮減頻率、時刻；h、hm分別為強迫沉浮運動的高度、高度振幅。

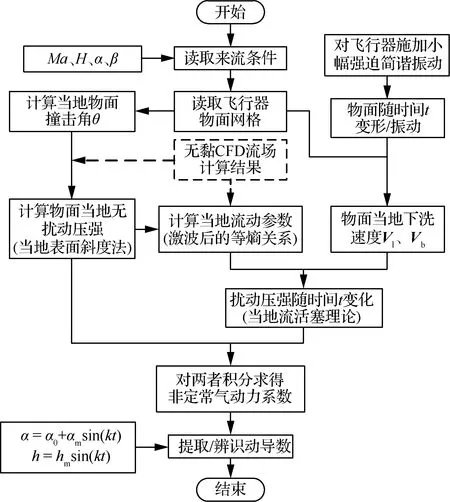
圖1 高速飛行器動導數高效預測流程

本文方法的優勢在于：采用當地表面斜度法及激波后的等熵關系式等求解飛行器表面流場參數，從而克服了傳統方法對CFD流場參數的依賴和耦合(圖1中虛線所示)。由于該方法不需要CFD方法求解定常流場，因此具有極高的效率；后文的算例也表明該方法具有較高的精度。因此本文方法可作為高速飛行器總體設計階段布局選型的工具。

值得說明的是，雖然本文在預測飛行器氣動導數過程中采用了基于牛頓撞擊理論的當地表面斜度法，但與“采用牛頓撞擊理論直接計算動導數”的工程近似法，兩者的原理不同：后者是將壓力系數對角速度(或迎角變化量)求導，再積分求出整個飛行器的動導數；本文方法是對飛行器施加強迫簡諧運動求出周期非定常氣動力，再對飛行器的非定常氣動力進行提取、辨識氣動導數。本文對飛行器施加強迫簡諧運動為風洞試驗、數值模擬計算動導數通用方法[19]。

2 非定常氣動力快速預測

2.1 當地流活塞理論的推導

本文基于當地流活塞理論對超/高超聲速飛行器非定常氣動力進行快速預測，首先對當地流活塞理論進行推導。

采用動量定理推導當地流活塞理論[20]，如圖2所示：考慮Ma?1的氣流經過飛行器表面，此時擾動可近似為沿物面法向傳播，如同氣缸中活塞隊氣流的擾動一樣。圖中：V、P、a分別為速度、壓強、聲速；下標∞、l、n分別表示自由來流、當地、法向的流動參數。

假設氣流受到物面變形或振動引起的擾動后速度在dt時間內變化dW，擾動傳播的距離為a·dt，則受到擾動氣體質量為ρaSdt(ρ為氣體密度，S為活塞面積)，受到擾動氣體的總動量變化為ρaSdt·dW。另外，活塞對氣體的沖量為dP·S·dt。根據動量定理可得

dP·S·dt=ρaSdt·dW

(1)

式(1)在當地流動參數下可簡化為

dP=ρlaldW

(2)

對式(2)積分，可得當地流活塞理論的壓力計算公式為

P=ρlalW+C

(3)

式中：常數C為附加擾動為0時的壓力；ρlalW為物面擾動時的壓力。

將附加擾動為0時的物面壓力用Psteady表示，又物面擾動可分為變形或振動，則當地流活塞理論的壓力計算公式可寫為

(4)

式中：n0為物面變形前的外法線單位矢量；n為物面變形后的外法線單位矢量；Vl和Vb分別為當地流動速度和物面振動速度；物面擾動速度W由物面變形速度Vl·δn和振動速度Vb·n組成。

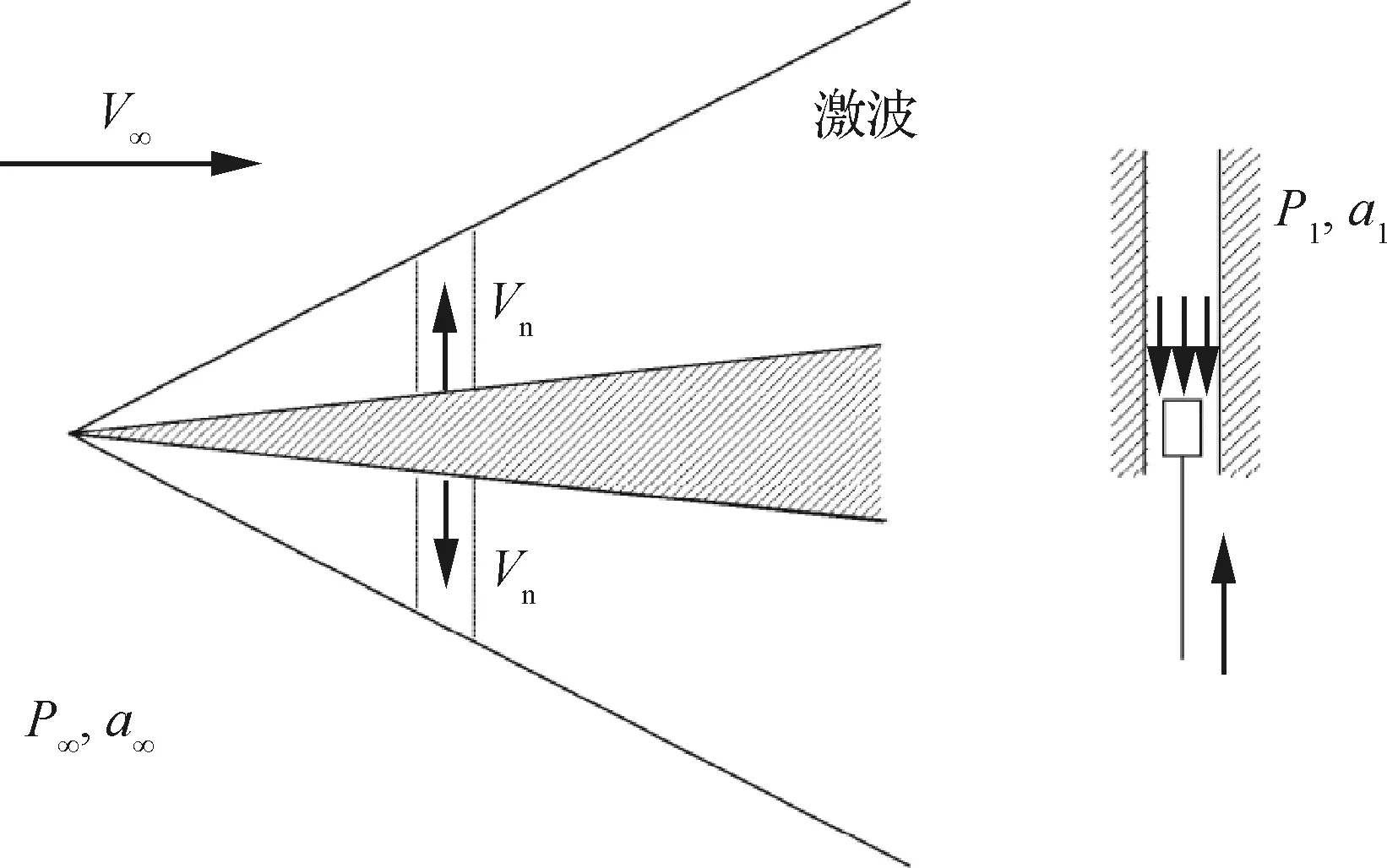
圖2 當地流活塞理論示意圖

與經典活塞理論相比，基于動量定理推導出的當地流活塞理論：① 推導過程中不需要級數展開，也就不存在忽略高階項的近似，因此精度比忽略高階項的活塞理論高；② 沒有活塞理論所必須的擾動速度小于來流聲速(W/a∞<1)的要求，因此當地流活塞理論只需滿足“擾動可近似為沿物面法向傳播”的假設即可，拓寬了馬赫數適用范圍的上限；③ 不需要等熵假設，這表明當地流活塞理論不僅可以用于大迎角、大厚度翼面問題，也可用于三維翼面、機身以及鈍前緣或鈍頭體存在弓形激波的情況。上述特點是當地流活塞理論可推廣用于機身和其他復雜外形的基礎[21]。

式(4)表明超/高超聲速飛行器非定常氣動力可分為無擾動項和物面變形/振動后的擾動項。下面分別介紹這兩項氣動力的計算方法。

2.2 氣動力無附加擾動項計算

對于無物面變形或振動擾動的高速飛行器，可看做定常流動，再用基于牛頓撞擊理論的當地表面斜度法計算氣動力無附加擾動項Psteady。具體方法為[22]：將飛行器表面離散、劃分為三角形面元網格，對每個面元區分為迎風面或背風面，再分別采取不同的公式進行計算。迎風面、背風面的劃分是根據自由來流條件及面元法矢共同確定的；此外，在面元判斷時加入了對“遮擋面元”的判斷，即采用光線投射算法(Ray-casting Algorithm)[23]判斷當前面元是否被遮擋。若為遮擋面元，則將該面元作為背風面處理。

對于迎風面，采用活塞理論與修正牛頓理論結合的方法進行計算[24]：

(5)

式中：B=(2/π)arctan[(Ma2+6)/10]；Cp,max為駐點壓力系數。

對于背風面，則采用普朗特-邁耶膨脹波方法：

(6)

式中：θ和γ分別為物面偏折角、氣體比熱比。

2.3 氣動力附加擾動項計算

求解氣動力附加擾動項時，需要用到當地流動參數。為求解方便，本文采用求解邊界層外緣的擾動壓力系數而不直接求解物面擾動壓力系數。又根據邊界層內的壓力梯度較小，可近似認為邊界層外緣的擾動壓力等于飛行器表面的壓力，因此所求出有效外形的非定常氣動力即為飛行器的非定常氣動力。

當地流動參數求解原理如下：對于完全氣體或平衡氣體，所有狀態參數(壓力、密度、溫度、焓、聲速、熵、流速、黏性系數)中只有兩個是相互獨立的，其他狀態參數均可根據相應的熱力學關系由這兩個參數求出。

2.3.1 正激波完全氣體邊界層外緣參數

對于大鈍頭體飛行器形成的正激波完全氣體，可認為進入邊界層外緣的流線基本是通過弓形激波的正激波部分。由于正激波后的熵在來流條件給定后是唯一確定的，因此，利用所得出的物面定常壓強和正激波后的熵這兩個獨立的狀態參數，可以確定其他邊界層外緣參數。

激波后的氣體壓力P2和密度ρ2可利用正激波前后關系式求得，即

(7)

(8)

式中：P∞為來流靜壓；ρ∞為來流密度。

利用等熵關系，求邊界層外緣密度ρe：

(9)

再用邊界層外緣的壓力和密度求出邊界層外緣的聲速：

(10)

求出邊界層外緣的當地密度和聲速以后，結合物面的變形或振動的下洗速度，即可根據式(4)計算出氣動力的附加擾動項。

2.3.2 斜激波完全氣體邊界層外緣參數

對于尖銳前緣、細長體飛行器外形，通過其頭部的激波是一道或數道斜激波，斜激波完全氣體后的壓力和密度可分別為

(11)

(12)

式中：β為激波角，可由θ-β-Ma圖表查出[25]，也可通過代數變換后的激波角顯示表達式求出[26]。

求出激波后的氣體壓力P2和密度ρ2后，再采用正激波完全氣體相同的方法求出邊界外緣的密度ρe和聲速ae。

對高溫平衡氣體而言，邊界層參數的確定要比完全氣體復雜。波后壓力P2、焓H2和密度ρ2相互依賴，不能用波前參數簡單求出，需要用迭代方法求解[27]。

3 氣動導數提取及辨識

以求解高速飛行器俯仰方向組合動導數為例，求解組合動導數，通常對飛行器施加小幅強迫簡諧定軸振動的運動形式。強迫簡諧運動方程為

α=α0+αmsin(ωt)

(13)

根據線化氣動力理論，俯仰力矩系數的泰勒展開表達式為

(14)

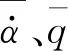
(15)

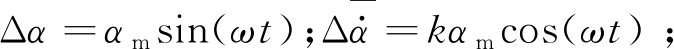
(16)

式中：Lref為參考長度。

由于式(15)中包含間接量Cm0、Cmα，因此無法直接求出組合動導數。文獻[28]給出了一種求解方法，將俯仰力矩系數表達式改寫為

Cm=A+Bsin(ωt)+Ccos(ωt)

(17)

式中：A、B、C為待定系數。在俯仰振蕩非定常周期計算后，可得到俯仰力矩系數隨時間的變化曲線，在曲線上任取3組不同時刻的數據即可求出A、B、C這3個系數。結合式(15)與式(17)，從而，俯仰組合動導數可表示為

(18)

式(18)即為本文結合當地流活塞理論與當地表面斜度法，采用強迫振動的運動方式求解俯仰組合動導數的公式。

為比較本文方法與“采用牛頓撞擊理論直接計算動導數”的工程近似法之間的差異，下面給出工程近似法求動導數的方法[24,29]。

飛行器在體軸坐標系下的來流速度為

V∞=V∞[cosαcosβ,sinβ,cosβsinα]

(19)

物面的無量綱外法向速度投影可通過向量積求出，即

(V⊥/V∞)=nxcosαcosβ+nysinβ+

nzcosβsinα

(20)

式中：nx、ny、nz為物面法向矢量的三分量；下標⊥表示速度在垂直物面方向的分量。

在俯仰方向，由角速度引起物面與氣流相對運動的導數為

(V⊥/V∞)q=(xnz-znx)/l

(21)

式中：l表示物面與飛行器參考點之間的距離。

則根據牛頓撞擊理論，物面壓力系數的角速度導數為

Cpq=Cp,max[1/Ma∞+1.2(V⊥/V∞)]·

(V⊥/V∞)q

(22)

面元ds上力矩系數的角速度導數為

dMyq=dFaq·z-dFnq·x

(23)

式中：

dFaq=Cpq·nxds,dFnq=Cpq·nzds

(24)

(25)

式(25)即為“采用牛頓撞擊理論直接計算動導數”的工程近似法。

4 典型算例驗證

分別在超聲速和高超聲速來流條件下選取典型算例對本文方法進行驗證，以考核本文方法在不同速域范圍內的適應性。

4.1 超聲速工況算例

在超聲速工況下，對有翼導彈(Basic Finner Missile，BFM)的俯仰組合動導數進行分析，目的是驗證本文方法超聲速工況預測動導數的精度以及效率。BFM是國際上驗證動導數計算的標準模型[30-31]，有比較成熟的實驗結果和工程估算結果。如圖3所示，BFM為尖錐形頭部、圓柱形彈身并帶有4個矩形尾翼的外形，尾翼為十字布局，圖中d為頭部直徑。

圖4為計算所用的有翼導彈面元網格，總網格量約為3.5×104。該算例的計算條件為：Ma=1.96，以頭部直徑為參考長度的雷諾數Red=0.187×106，質心位置取外形縱向總長的61%處。

圖5為不同方法對有翼導彈的動導數預測結果對比，其中風洞試驗數據來源于文獻[30]；CFD數據為文獻[32]采用非定常CFD差分法的結果；準定常方法為對飛行器施加準定常定軸旋轉運動的工程近似結果。從圖中可以看出：在超聲速工況下本文方法能夠較好地反映有翼導彈動導數隨迎角變化規律，精度也比工程近似方法有較大的提高。

圖3 有翼導彈幾何外形示意圖

圖4 有翼導彈面元網格

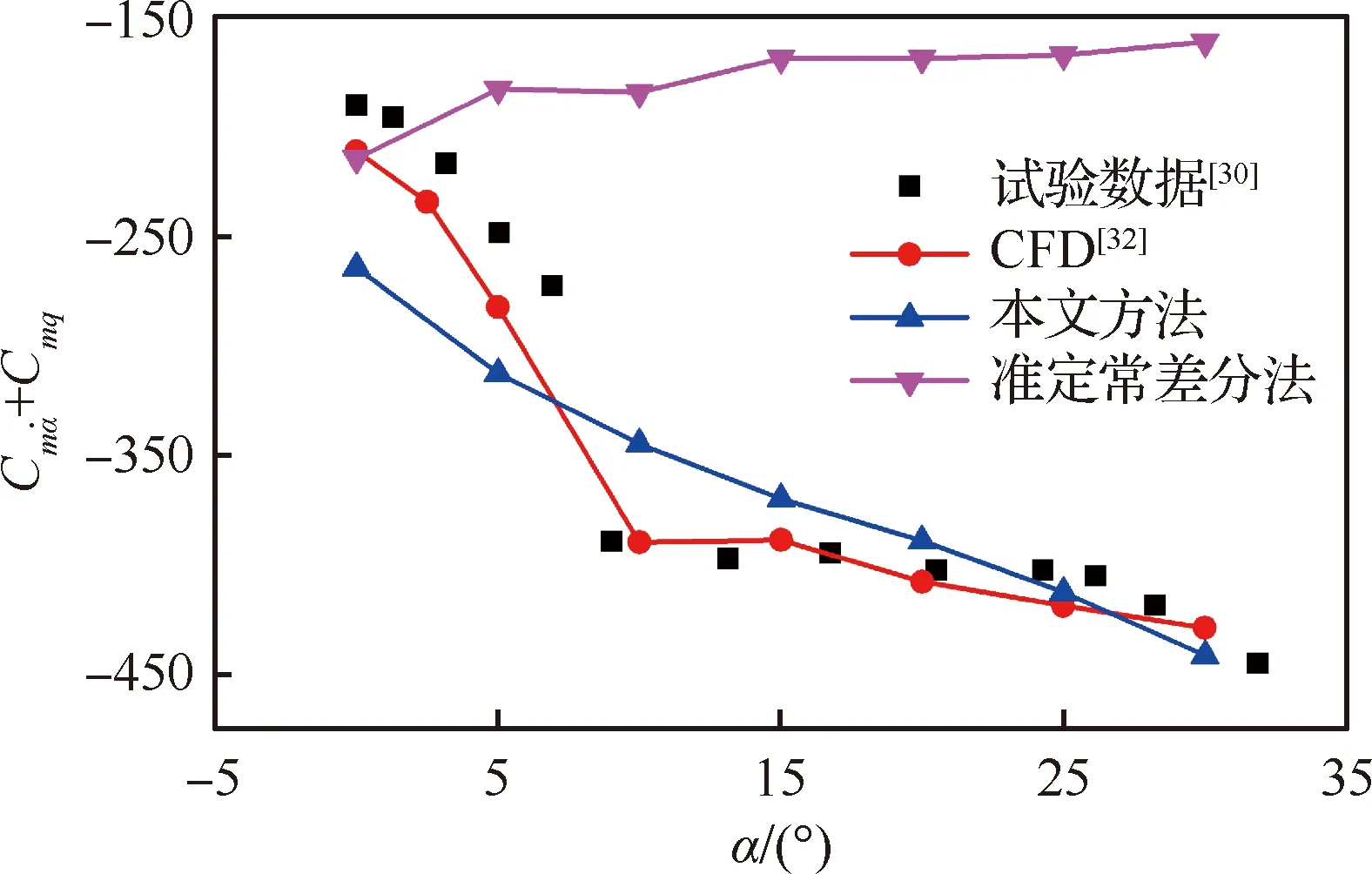
圖5 有翼導彈動導數預測結果對比

表1為不同方法動導數計算效率對比。其中：非定常周期計算、非定常差分法預測動導數的耗時來源于文獻[32]；本文方法在Intel Core i7-8700 3.20 GHz單核上運行，僅需約5 s就能獲得所有工況的結果，表明本文方法具有極高的效率。特別的是，本文方法僅需要提供面元網格、不需要生成體網格，這節約了復雜外形體網格生成工作量與時間。

表1 不同方法動導數計算效率對比

Table 1 Efficiency comparison of different methods for dynamic derivatives computation

方法耗時非定常CFD周期計算[32]61 h非定常CFD差分法[32]12 h本文方法～5 s

4.2 高超聲速工況算例

在高超聲速工況下，選擇彈道外形(HyperBallistic Shape, HBS)進行俯仰組合動導數預測，目的是驗證本文方法高超聲速工況下預測動導數的精度。

HBS標模是AGARD用來測定高超聲速飛行器穩定性的典型外形。如圖6所示，HBS由三段長均為1.5d′(d′為球體直徑)的球柱、5°半錐角的圓錐段和15°半錐角的圓錐段組成，其俯仰動導數具有較為精確的試驗結果[33]，通常被用來衡量高超聲速工況下動導數計算結果的準確程度。

圖7為彈道外形面元網格，總網格量約為2×104。 該算例的計算條件為：Ma=6.85，以頭部直徑為參考長度的雷諾數為Red′=0.72×106，質心位置取外形縱向總長的72%處。

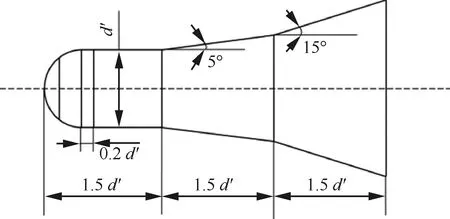
圖6 彈道外形示意圖

圖7 彈道外形面元網格

圖8為不同方法對彈道外形的動導數預測結果對比，其中風洞試驗數據來源于文獻[33]；CFD數據為文獻[34]采用非定常CFD方法的結果；準定常方法為對飛行器施加準定常定軸旋轉運動的工程近似結果。從圖中可以看出：在高超聲速工況下本文方法能夠較好地反映動導數隨迎角變化規律，而工程近似方法只能反映動導數的量級。

為了考察網格密度對本文方法的影響，將本算例模型分別劃分為粗糙、中等、加密3種不同密度的網格，以比較不同網格量下的動導數預測結果。不同網格在0°迎角下的動導數對比如表2所示。

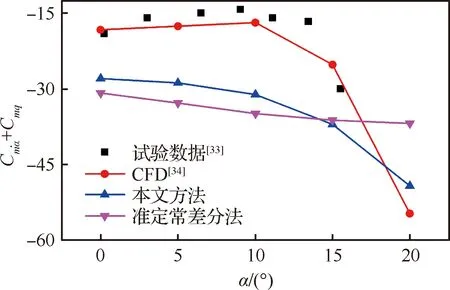
圖8 彈道外形動導數預測結果對比

表2 不同網格密度對計算結果的影響

從表2可以看出，在面元網格能夠描述基本飛行器氣動外形的前提下，網格量變化對本文方法影響十分微小(不超過0.8%)。

在計算效率方面：使用非定常的雙時間方法計算本算例單個工況的俯仰動導數耗時為16 h，結合CFD和當地流活塞理論的方法耗時約為40 min[18]，本文方法計算單個工況的動導數平均不超過1 s，表明了本文方法具有極高的效率。

5 復雜外形飛行器氣動導數預測

為了驗證本文方法對復雜外形飛行器動導數預測的適用程度，以類X-37B飛行器為研究對象，分別采用本文方法和基于定常CFD的當地流活塞理論方法預測類X-37B飛行器的動導數，并與施加強迫振動的非定常CFD方法作對比。

X-37B是美國為了驗證可重復使用空間技術和在軌空間飛行任務而啟動的項目[35]，并計劃在X-37B飛行器技術基礎上繼續進行能夠投送6名宇航員進入太空的X-37C計劃[36]。因此，以類X-37B飛行器為對象研究高速飛行器氣動導數具有典型的意義。圖9為類X-37B飛行器示意圖。

圖10為類X-37B飛行器動導數預測結果對比，其中CFD方法為文獻[37]對飛行器施加小幅強迫振蕩的非定常CFD結果；“無黏CFD+當地流活塞流理論”為基于定常CFD流場數據，采用當地流活塞理論計算非定常氣動力，再對動導數進行提取、辨識方法得到的結果。通過圖10可以看出：本文方法很好地預測出了類X-37B飛行器的動導數隨迎角變化規律，精度與“無黏CFD+當地流活塞流理論”方法相當，但本文方法效率遠高于后者。

圖9 類X-37B飛行器示意圖

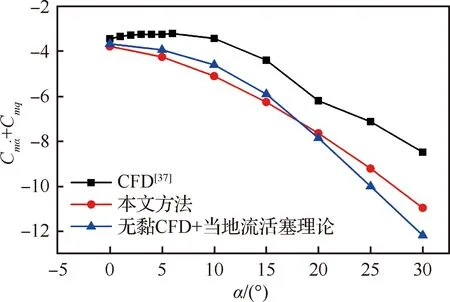
圖10 類X-37B飛行器動導數預測結果對比

由于“無黏CFD+當地流活塞流理論”提取、辨識動導數方法與本文方法相同，因此兩者結果的誤差來源可能是無黏CFD流場與本文“當地表面斜度法+激波后等熵關系”計算出的流場不一致造成。如式(4)所示：在使用當地流活塞理論計算非定常氣動力時，用到了兩個重要的流場參數：邊界層外緣密度及邊界層外緣聲速。因此，本文對邊界層外緣密度及邊界層外緣聲速進行對比分析。

圖11、圖12分別為上述兩種方法得出的邊界層外緣密度與邊界層外緣聲速對比(α=30°)。從圖中可以看出，兩種方法計算出的流場大面積分布較為一致，但在駐點、翼前緣附近有較大差別。這應是兩種方法預測動導數誤差的來源。

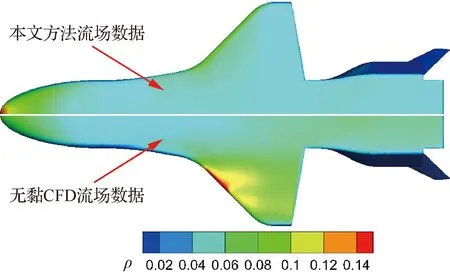
圖11 邊界層外緣密度對比

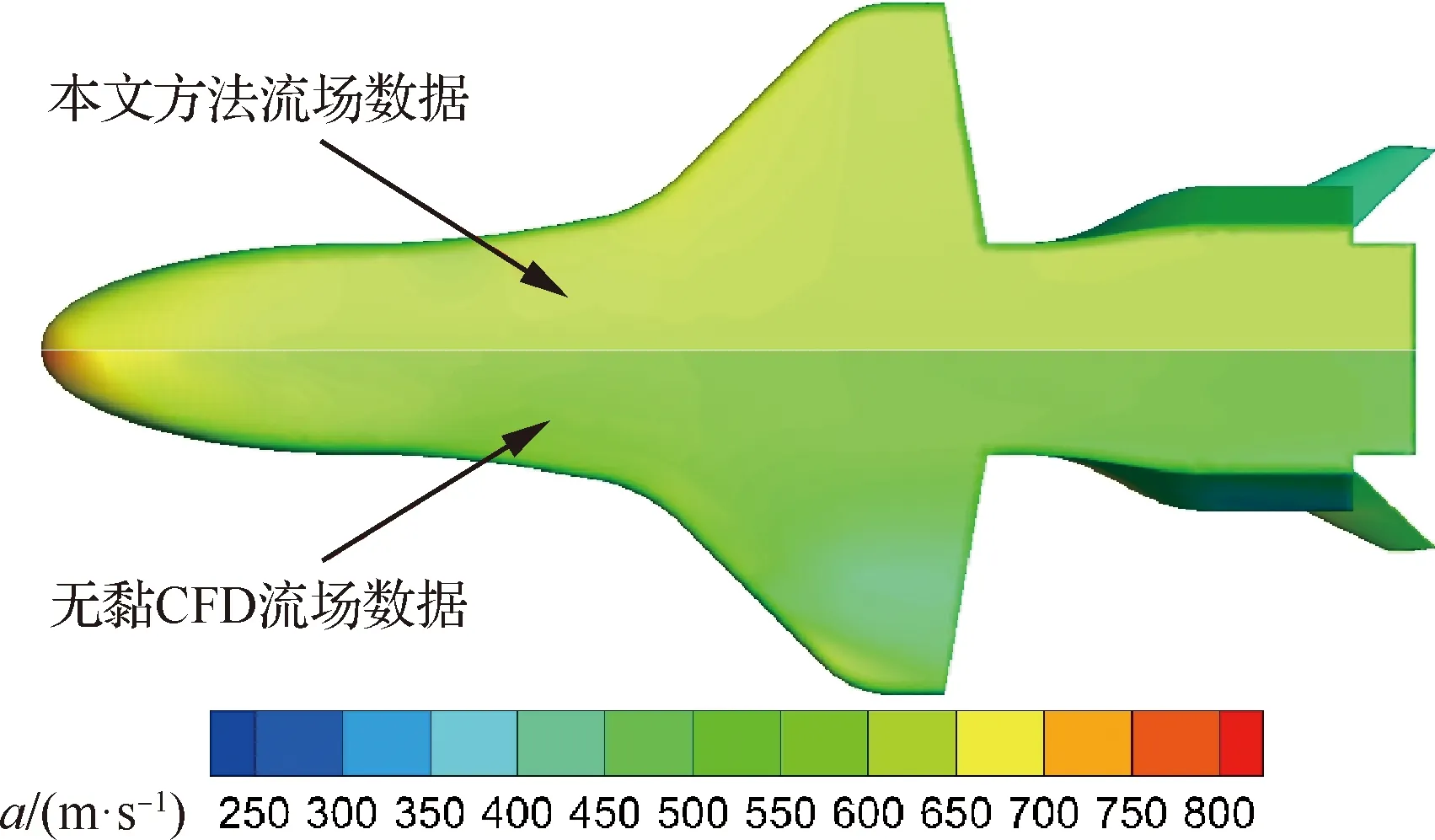
圖12 邊界層外緣聲速對比

6 結 論

1) 本文動導數預測方法是基于“當地流活塞理論”及“牛頓撞擊理論”等相關理論推導而出，因此“當地流活塞理論”及“牛頓撞擊理論”的成立條件決定了本文方法適用的速域范圍，即擾動可近似為沿物面法向傳播的超聲速/高超聲速流動。

2) 當地流活塞理論推導過程中不需要等熵假設，拓寬了經典活塞理論對飛行器外形和迎角的適用范圍，因此本文方法可用于復雜外形飛行器的動導數預測。

3) 本文方法避免了傳統動導數預測方法對CFD流場的依賴、耦合，從而大幅提高了計算效率；同時在面對復雜外形時也能較好地得出動導數隨迎角的變化規律，精度能夠滿足飛行器總體設計階段的要求，可作為飛行器布局選型階段的工具。