精鍛成形身管力學性能預測分析與工藝優化

畢夢凡，方 峻，樊黎霞，扶云峰，任青松，張必良

(南京理工大學, 南京 210094)

精鍛成形工藝是一種精確高效的身管制造工藝，能保證最高的成形與性能質量[1]。身管作為一種空心厚壁圓管，彈丸發射時膛內受到高溫高壓火藥燃氣的影響，工作環境惡劣，對其壽命等產生了極大的影響。試驗證明，合理的身管鍛造工藝可以有效地提高身管性能[2]。目前，在精鍛成形工藝參數對身管鍛后性能的影響方面已經作了大量的研究，包括線膛部分工藝參數對鍛后性能影響[3]和彈膛部分工藝參數對鍛后性能影響[4]，鍛造比對膛線成形質量的影響[5]等。在分析鍛后身管力學性能時，通過試驗研究過程繁瑣且周期較長，并且沒有統一的評價方法。在國內，鍛造工藝對身管鍛后力學性能影響[6]方面的研究幾乎為空白，尤其缺乏一種預測身管鍛后力學性能的合適模型。合適的身管鍛造工藝參數可以保證身管在成形后的力學性能要求。在身管設計尺寸和鍛透性要求的前提下需要對身管進行試驗分析，使其滿足力學性能要求[7]。經大量試驗研究，發現鍛造比是影響身管線膛精鍛力學性能的主要因素，精鍛成形過程包括兩個階段，下沉段和鍛造段，分別對應下沉段鍛造比和鍛造段鍛造比[8]。為測試精鍛成形身管力學性能，測定各項力學性能指標水平，本文對鍛后身管進行拉伸與脹形試驗，分別對應縱向性能和橫向性能：縱向性能包括屈服強度、抗拉強度、斷面收縮率、延伸率，橫向性能包括屈服強度和延伸率[9]。為了使鍛造試驗數據更具有代表性，對過程參數基于軟件Design-Expert試驗設計，運用響應面模塊分析鍛造比參數與力學性能指標[10]，擬合精鍛成形身管函數模型。綜合步兵自動武器及彈藥設計手冊[11]與非標脹形試驗的橫向力學性能的重要性，確定身管鍛后力學性能各指標設計規范。

1 基本理論與方法

精鍛成形身管的力學性能預測、評估與優化包括各指標力學性能預測、身管力學性能合格性評估與鍛造過程參數優化3部分。通過建立身管響應面曲面方程預測下沉段鍛造比與鍛造段鍛造比對各指標力學性能的影響。利用響應面分析擬合試驗數據，根據R2回歸系數選擇擬合精確的模型。分析與優化流程如圖1所示。

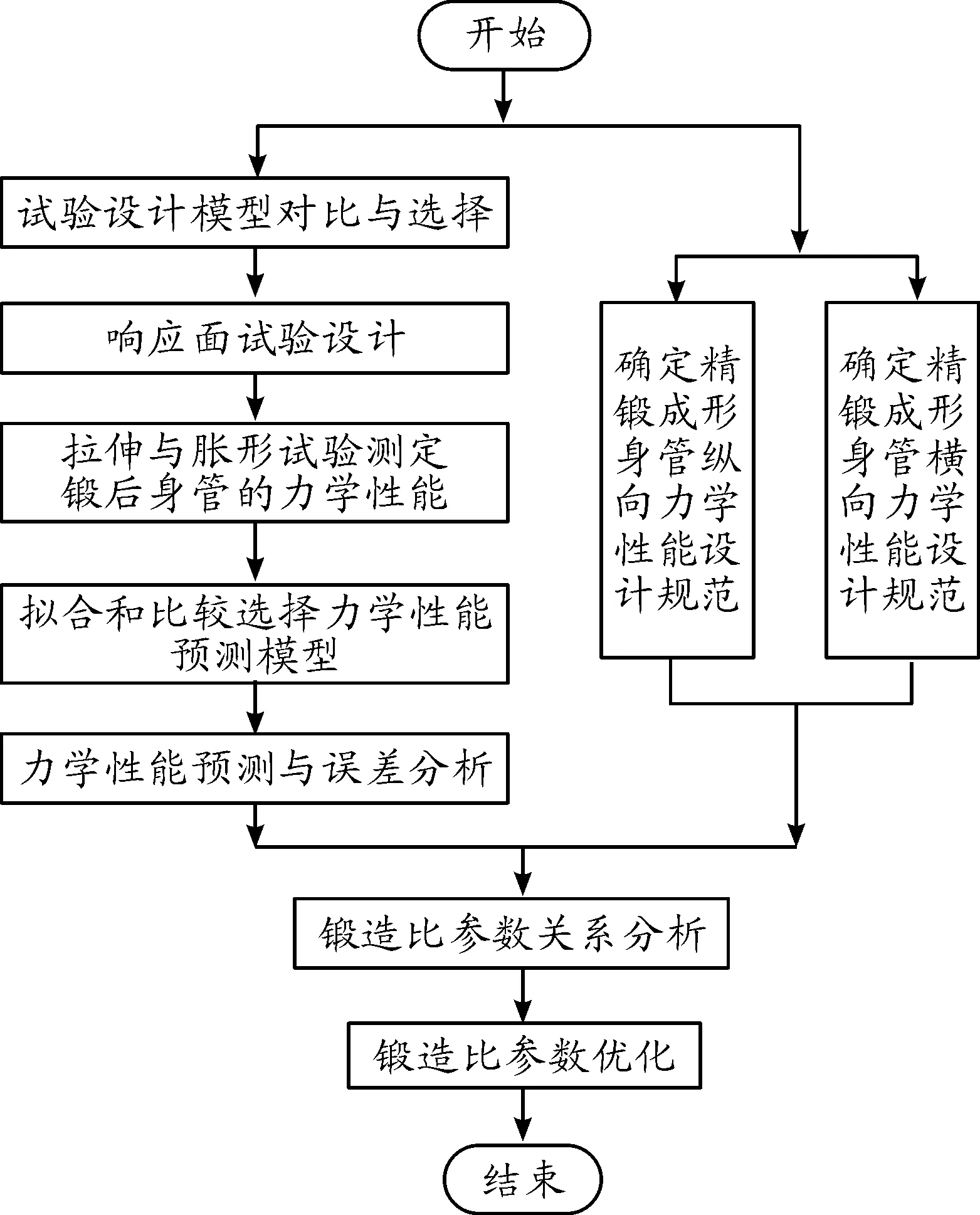
圖1 身管性能分析與優化流程框圖

為測定精鍛成形身管力學性能數據，對身管進行性能試驗，選擇鍛造過程參數不同的身管進行拉伸與脹形試驗，測定了縱向屈服強度、縱向抗拉強度、縱向延伸率、縱向斷面收縮率、橫向屈服強度和橫向延伸率，鍛造過程參數與測量數據如表1所示(以橫向延伸率為例)。

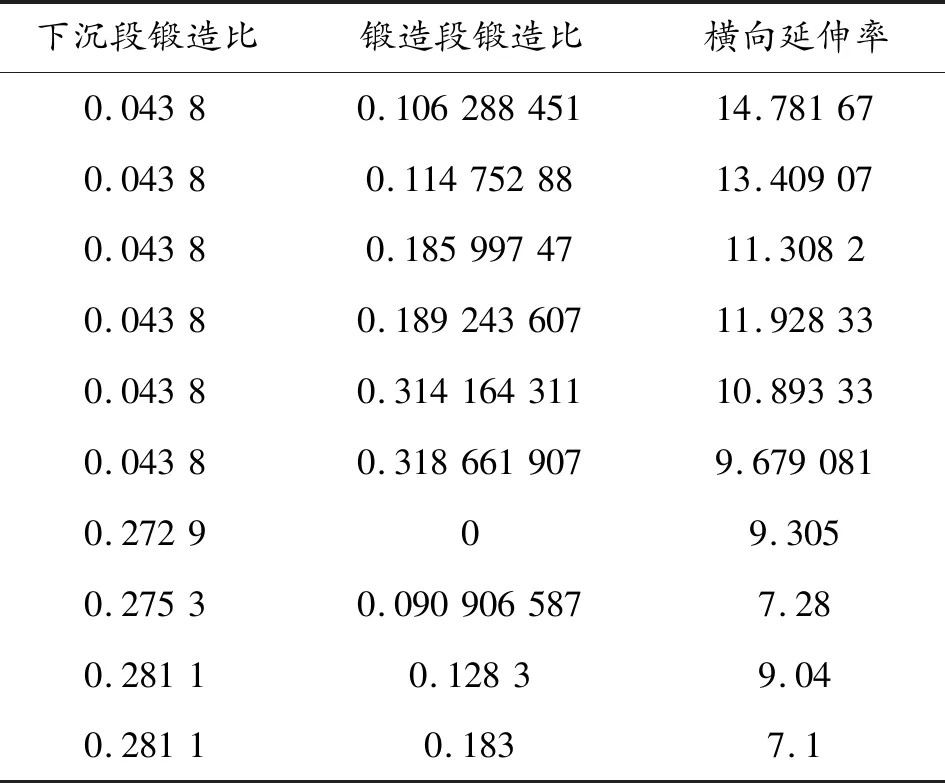
表1 試驗測量數據 %

身管徑向精鍛過程是累積塑性變形，身管鍛造比參數與彈塑性性能存在一定的關系。通過Design-Expert中的響應面分析可知，根據階數的不同多項式有多種表現形式，根據是否考慮平方項和交叉項可分為Quadratic和2FI兩種。

由試驗數據和材料特性可知，橫向延伸率值在7～15。在軟件Radial Forge中對Quadratic模型擬合結果可知，多元非線性回歸的殘差平方和為 1.982 794 399 716 46，R2回歸系數(模型擬合精度)為 0.964 464 624 643 217，擬合結果滿足精度要求，但是在驗證模型仿真與數據時發現橫向延伸率畸變為負值，如圖2所示，但是2FI模型不會發生，橫向延伸率數值滿足變化規律。

Quadratic函數模型使樣本數據失真，力學性能值產生畸變，所以選擇考慮交叉項而不考慮平方項的2FI模型。2FI函數模型的一般形式y1不僅考慮了下沉段鍛造比和鍛造段鍛造比對鍛后力學性能的影響，同時考慮了交叉項對鍛后力學性能的影響，特殊形式y2則未考慮鍛造比參數交叉項的影響。

y1=ax1+bx2+cx1x2+d

(1)

y2=ax1+bx2+d

(2)

x1為下沉段鍛造比；x2為鍛造段鍛造比。

Design-Expert軟件響應面分析分為兩個部分，第一部分是Design，為了更匹配過程參數的設計規律，試驗設計方法選擇Miscellaneous，設計類型為Pentagonl，中心點為3，第二部分為Analysis，對拉伸、脹形力學性能數據運用非線性數據擬合方差獲得響應面曲面方程并利用R2回歸系數對擬合效果和有效性進行評估。R2回歸系數表征模型擬合精度，并以此為依據選擇擬合精確的模型。其中R2回歸系數與性能指標成正比關系，系數越高擬合準確度越高。

(3)

式中：k表示試驗設計組數；xi為響應面模型計算值；yi為試驗數據值；yaver為試驗數據平均值。

當多組力學性能數據擬合模型并選型時，每組數據擬合得到兩種響應面曲面方程和兩組回歸系數。在多數據擬合模型選型時，對各組試驗樣本的參數求均值AVGi，利用參數AVGi表征模型擬合的準確度，如表2所示。

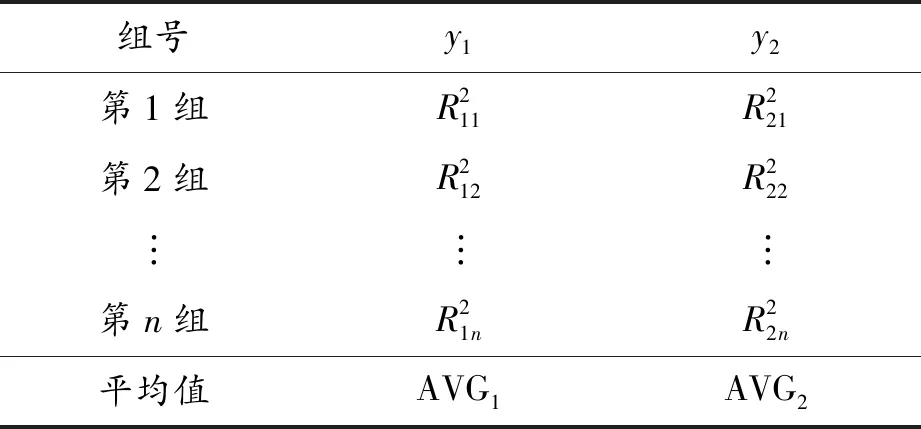
表2 擬合準確度

各組數據非線性擬合方程準確度均值為AVGi，AVGi由式(4)可得：

(4)

AVGi：表示同一組數據的R2回歸系數均值；表征模型擬合精度，且與擬合效果和有效性成正比，值越大模型擬合越準確。

2 力學性能預測與誤差分析

2.1 建立預測模型

對精鍛成形身管進行拉伸、脹形試驗得到力學性能數據，運用響應面函數表達式對試驗數據擬合，并得到R2回歸系數。由擬合結果可知，響應面曲面方程y1、y2擬合R2回歸系數，方程y2擬合精度都高于y1，考慮下沉段鍛造比和鍛造段鍛造比的參數交叉項提高了響應面擬合效果和可靠性，所以響應面擬合選擇模型y1。

根據擬合響應面曲面方程可知鍛后身管力學性能方程系數如表3所示。

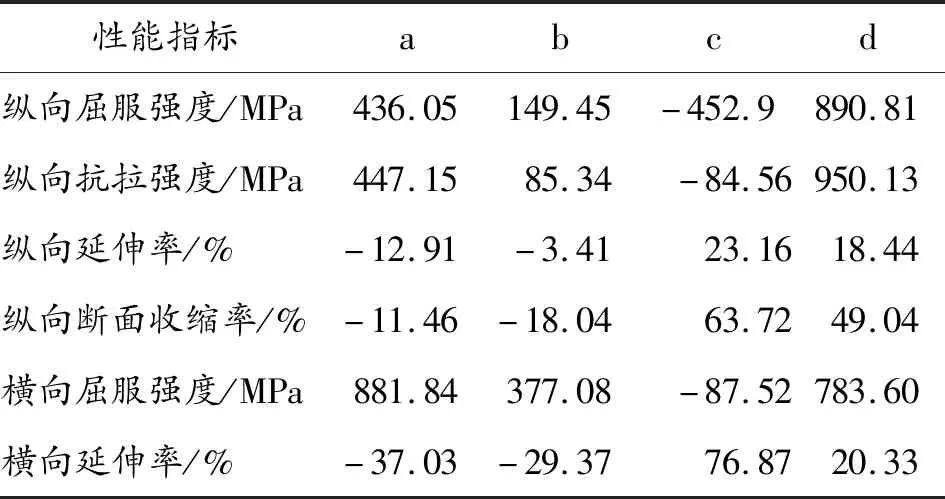
表3 精鍛成形身管方程系數

2.2 模型誤差分析

身管內膛徑向精鍛成形是毛坯根據芯棒形狀與尺寸在精鍛機錘頭高頻率鍛打下累積塑形變形的結果。在精鍛成形中給定芯

棒和毛坯的設計尺寸，根據給出的鍛件尺寸和過程參數使成形身管達到力學性能要求。

對試驗身管毛坯進行編號記錄毛坯參數，對鍛造過程參數進行試驗設計，選擇實測直徑為5.76 mm的芯棒在相同精鍛成形過程下對毛坯鍛打，記錄試驗數據，見表4所示。

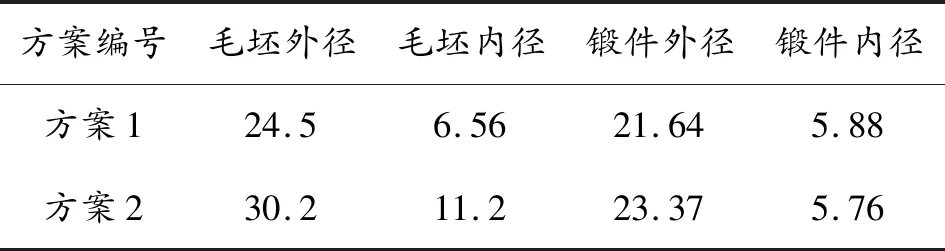
表4 方案編號 mm

根據毛坯、芯棒和鍛件參數由鍛造比公式可得各方案鍛造比[5]：

下沉段鍛造比公式：

(5)

鍛造段鍛造比公式：

(6)

精鍛成形身管力學性能預測包括純線膛精鍛成形身管和彈線膛精鍛成形身管預測兩部分，為全面驗證身管鍛后力學性能預測的可靠性[13]，設計方案1為純線膛身管鍛件，方案2為彈線膛身管鍛件。方案一總鍛造比為22.12%，下沉段鍛造比為4.3%，鍛造段鍛造比為18.60%；方案2總鍛造比為34%，下沉段鍛造比為28.11%，鍛造段鍛造比為8.12%。各方案力學性能誤差分析如表5所示。

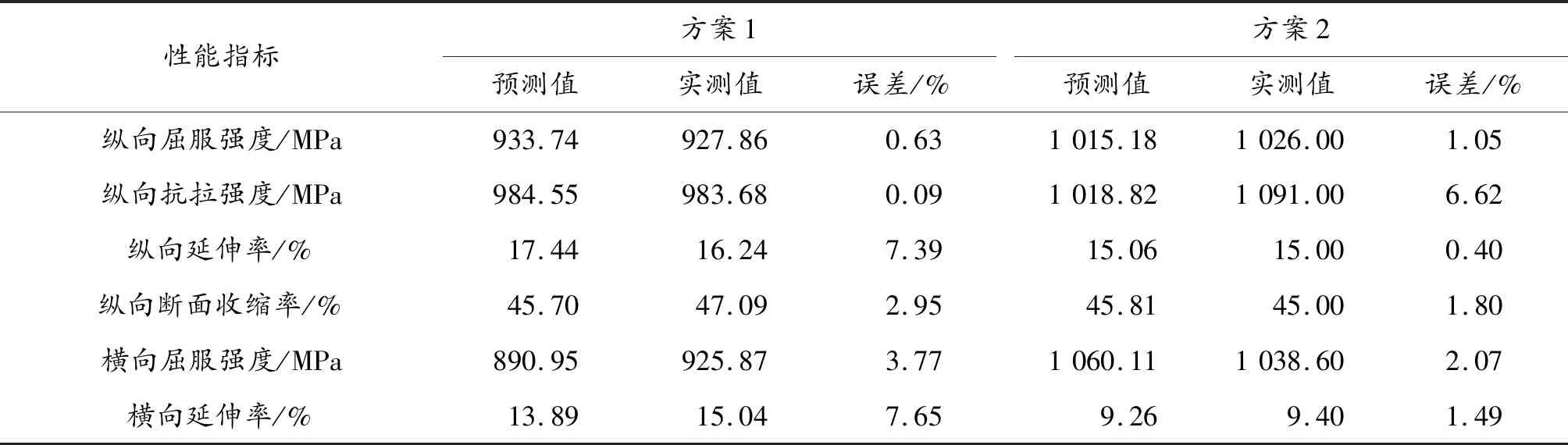
表5 各方案誤差分析

由誤差計算公式可知身管鍛后力學性能預測值與實際值的誤差小于10%(因樣本有限，設置閾值為10%)，所以認為擬合響應面曲面方程是符合要求的。根據各方案預測結果可以得出彈線膛同鍛預測誤差小于純線膛，所以彈線膛預測更準確。由大量試驗結果可知，徑向精鍛過程對橫向力學性能要求更高，彈線膛同鍛力學性能預測誤差在3%之內，所以預測與評估結果可靠性更高。

3 身管評估與過程參數優化

3.1 身管力學性能評估

為了確定精鍛成形身管合格性評估規范，查詢了步兵自動武器及彈藥設計手冊[11]關于縱向力學性能的要求，考慮到徑向精鍛過程橫向力學性能對鍛后力學性能的重要性，總結了大量試驗結果，給出了身管鍛后力學性能指標設計要求，如表6所示。

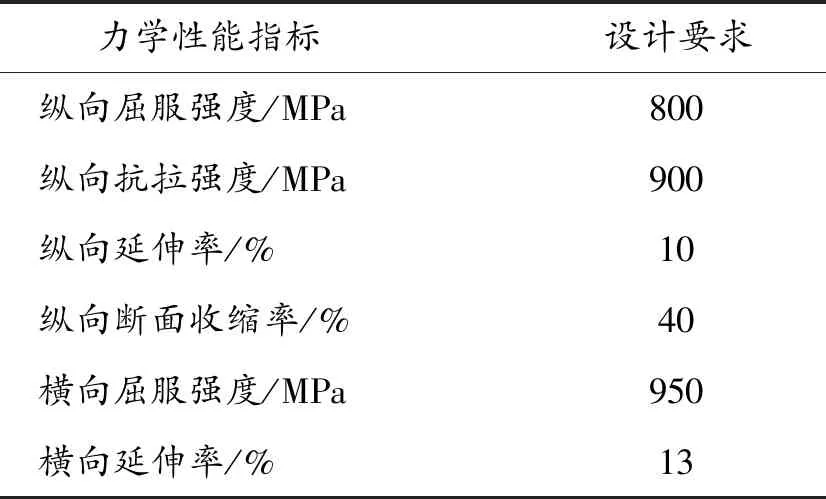
表6 輕武器結構鋼力學性能指標

由試驗驗證方案與身管鍛后力學性能設計要求可知，方案一與方案二的縱向力學性能都滿足設計要求，但是方案一的橫向延伸率滿足要求而方案二的橫向延伸率不滿足要求，所以身管徑向精鍛過程著重考慮身管橫向力學性能要求。

3.2 鍛造比參數關系分析

精鍛成形身管力學性能中橫向性能是主要影響因素，根據橫向延伸率的設計規范，得到鍛造比參數關系與設計取值范圍，如圖3所示。

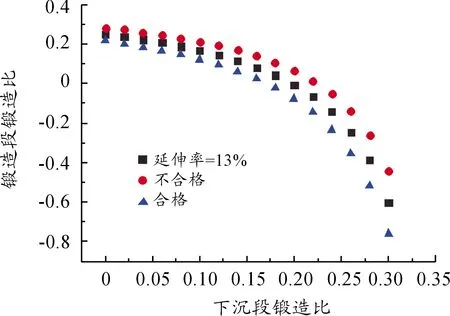
圖3 鍛造比參數關系圖

由身管參數設計圖可知散點為方塊的曲線為身管橫向延伸率合格時的邊界曲線，當下沉段鍛造比一定時，鍛造段鍛造比在曲線下方說明身管合格，在曲線上方說明身管不合格，同時也可對優化結果進行驗證。

身管精鍛過程給定了毛坯與芯棒參數，鍛件的關鍵點徑向尺寸由下壓量決定，下壓量由下沉段鍛造比與鍛造段鍛造比決定，所以根據力學性能指標建立合格身管的鍛造比參數設計圖時，當下沉段鍛造比一定時，可以得到鍛造段鍛造比合格區域，即下壓量范圍。

3.3 鍛造比參數優化

1) 歸一化處理

為了統一度量單位，加快訓練網絡的收斂性，把有量綱量變為無量綱量，將數據映射到0～1處理。

X=[x1,x2]T

(7)

(8)

2) 目標函數

為了得到最優過程參數，利用加權系數法將多目標優化問題轉為單目標優化問題，優化目標為綜合力學性能，在滿足約束的情況下其值越大越好。

(9)

(10)

3) 約束

根據設計規范對各過程參數與優化變量約束如下：

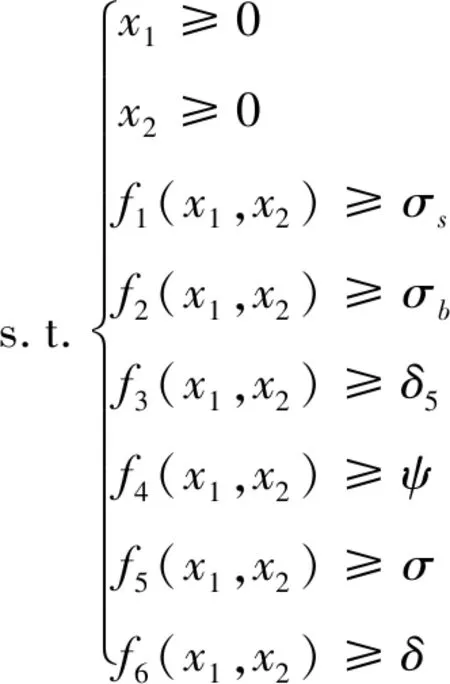
(11)

4) 優化

已知力學性能的響應面曲面方程，添加邊界約束條件與橫、縱向力學性能約束條件建立綜合力學性能功能函數，采用非線性約束最小值優化[12]得到最優過程參數。

根據非線性約束優化可知下沉段鍛造比為t1=0.148 7，鍛造段鍛造比t2=0.096 7，綜合力學性能為fmax=0.59。由鍛造比參數關系分析曲線可知，優化結果在合格范圍之內，所以身管過程參數優化結果滿足設計要求。同時參數t1遠大于0，所以該鍛造比屬于彈線膛鍛造過程參數，由彈線膛身管鍛透極限圖可知鍛造鍛造比邊界值為7%[3]，所以參數t2為9.67%滿足彈線膛同鍛鍛透極限。

4 結論

基于響應面對拉伸與脹形試驗力學性能數據建立曲面方程，表征鍛造比參數對力學性能的影響規律。 總結大量試驗結果建立了身管鍛后力學性能包括橫向與縱向力學性能的設計規范，判斷精鍛成形身管在一定的過程參數下的力學性能。

對綜合力學性能采用非線性約束優化得到最優過程參數與綜合力學性能極值。由彈線膛同鍛身管鍛透極限圖可知，優化結果為鍛造段鍛造比為9.67%滿足鍛透極限準則。建立了力學性能各指標鍛造比參數取值范圍，根據橫、縱向力學性能的設計邊界值確定了關鍵過程參數范圍，即錘頭鍛打下壓量的取值范圍。

根據試驗結果可知模型預測與實際值的誤差在允許范圍之內，所以響應面模型可以用于精鍛成形身管力學性能預測。