基于樣本分位數原理的飛參數據異常值檢測算法
戴邵武,陳強強,2,毛 凱,戴浩然
(1.海軍航空大學,山東 煙臺 264000; 2.海軍92728部隊,上海 200040;3.空軍95596部隊,河南 商丘 476000)
飛行數據記錄系統(Flight data recorder system,FDRS)起源于20世紀40年代,FDRS通過記錄并保存飛機在飛行過程中的一些重要參數(一般稱為飛參數據),實現對飛機狀態的實時及事后檢測[1]。飛參數據為飛機故障調查、研發設計以及訓練維護提供了重要的數據來源。因此,通過對飛參數據進行準確有效的處理分析,是提高飛機可靠性的重要途徑之一[2]。
在對飛參數據進行分析的過程中,受到飛行環境、儀器內部高精密、高復雜尺度的構造以及噪聲干擾等多方面因素的制約,飛參數據在記錄過程中會受到一定的影響[3]。通常情況下,將這些受到外界干擾而導致的飛參數據中的數據異常跳變點稱為野值[4]。野值數據一般偏離記錄數據的變化規律,野值的存在會給飛參數據狀態估計及飛行性能分析帶來較大的誤差,甚至嚴重偏離飛機的實際飛行狀態。因此在飛參數據實際使用過程中,必須對野值進行處理,從而最大限度地保證飛參數據的準確性[5]。
隨著對飛參數據野值檢測方面研究的不斷深入,一些數學方法逐漸得到應用。其中最常用也最簡單的判別準則即萊特準則[6](Letters criterion,3σ準則)。萊特準則通過對隨機誤差正態分布規律進行研究以進行野值剔除,但其在處理過程中假定所有觀測樣本均服從同一正態分布,這在一定程度上制約了適用性。文獻[7-8]通過構建卡爾曼濾波器(Kalman Filter)實現對野值的識別和處理,但Kalman濾波方法需要對過程噪聲及量測噪聲有著明確的定義,不滿足飛參數據的實際情況。文獻[9]通過構建觀測器/卡爾曼濾波,在無需系統噪聲情況下實現了野值剔除,但該方法同樣依賴于已知的系統模型。
隨著對信號處理的不斷深入研究,時頻分析方法在野值剔除中得到了應用。文獻[10]與文獻[11]通過引入小波變換(Wavelet Transform,WT)對遙測、飛參數據進行分解并重構,得到了較好的野值剔除效果。文獻[12]通過小波變換與Letters準則的結合,實現了對遙測數據的野值剔除與降噪。但小波分析的局限性在于小波基的選取,復雜的小波基選取對小波性能的影響至關重要,有時為了得到較好的分解結果甚至會單獨構建相應的小波基,給研究過程帶來了額外的計算量。文獻[13]通過經驗模態分解(Ensemble Empirical Mode Decomposition,EEMD)與希爾伯特變換(Hilbert Transform,HT)相結合的方法實現了飛參數據的時頻分析,EEMD方法雖然在一定程度上緩解了經驗模態分解(Empirical Mode Decomposition,EMD)的模態混疊問題,但其完備性不足的問題,在一定程度上造成了數據的缺失,影響了飛參數據的精度。
本文通過對樣本分位數原理的分析研究,構建時間窗口對飛參數據遍歷并進行樣本分位數求解;通過分析樣本分位數的遍歷效果對飛參數據異常值進行檢測。最后采用樣本分位數方法對實際飛參數據進行分析,以實現對飛參數據的野值剔除。樣本分位數的計算方法簡單,無須進行復雜的參數及內部設置;僅對時間序列進行分析的特性使其對數據信息要求較少,是一種簡單而有效的異常值檢測方法。
1 飛參數據異常值檢測
1.1 飛參數據異常值
根據實際情況不同,對于異常值的定義也有所不同。目前常用的定義是由Barnett與Lewis于1984年所提出的異常值定義方法:一個觀測數據集中與其他數據表現不一致的一個或多個觀測點所組成的子集[14]。
在飛參數據采集過程中,受到惡劣的飛行環境影響,不可避免地存在個別錯誤數據,異常值的存在,為后續飛參數據的處理工作帶來了很大的困擾,影響著飛參數據處理的精度,甚至會帶來嚴重偏差。這些數據值可能偏大或偏小,甚至會出現丟失情況,如圖1中A、B點所示。

圖1 數據序列的異常值示意圖
通過對圖1飛參數據異常值的分析可知,異常值的出現位置隨機且大小未知,因此無法直接通過固定時間點或固定位置的監測實現飛參數據異常值的檢測。但異常值的出現,在一定程度上對野值點附近的數值造成了影響,因此,可采用樣本分位數對飛參數據序列進行分析。樣本分位數是與總體分位數相對應的樣本特征,反映一定比例數據集中位置的統計數據的數學特征[15]。通過對樣本分位數的分析,可以統計出野值點附近的數據信息,以實現對野值點檢測。
1.2 樣本分位數
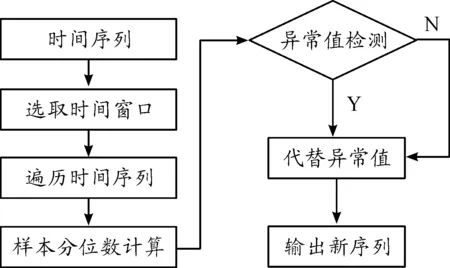
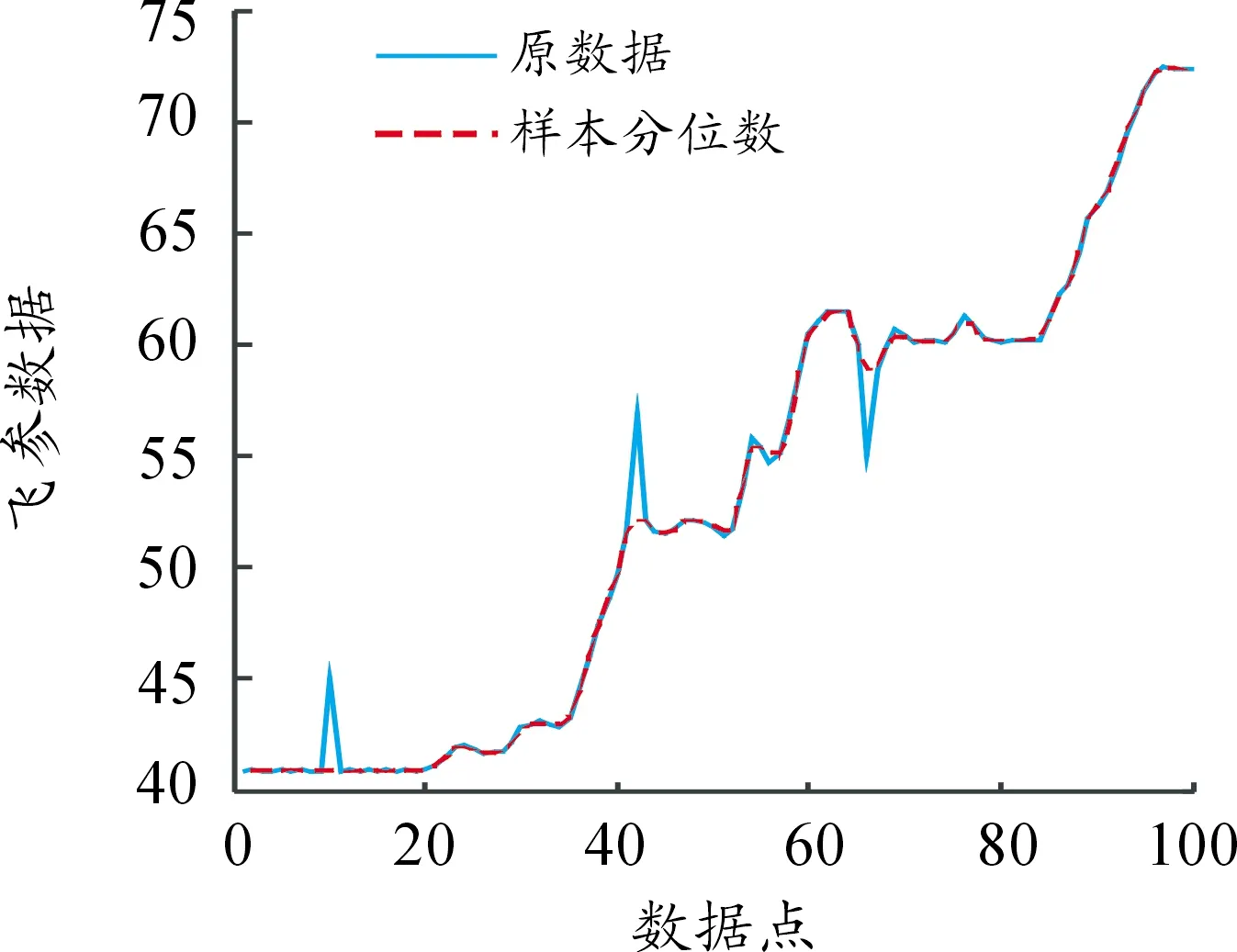
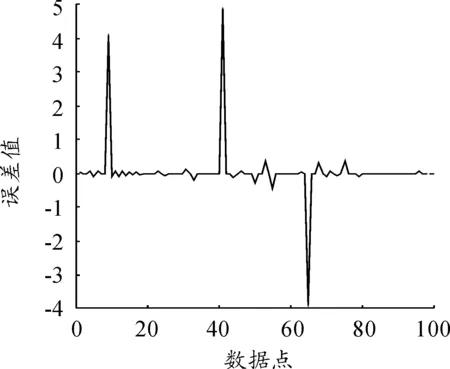
對于總體數據X及給定的a(0 圖2 a分位數示意圖 對于總體數據X,若X分布關于y軸對稱,且存在對應的xa/2,滿足P{X≥xa/2}=a,則稱xa/2為X分布的雙側a分位數(雙側臨界值)。如圖3所示。 圖3 雙側a分位數示意圖 根據圖2、圖3中對分位數的定義,引入四分位數概念(Quantile),在統計學中,將總體數據X中所有數值從小到大排列并分成四等份,出于3個分割點位置的就是四分位數[17]。其中,第一四分位數也叫做“較小四分位數”,等于樣本X中所有數值從小到大排列后的第25%的數字;第二四分位數也叫做“中位數”,等于樣本X中所有數值從小到大排列后的第50%的數字;第三四分位數也叫做“較大四分位數”,等于樣本X中所有數值從小到大排列后的第75%的數字。 根據定義可知,樣本分位數是一個非參數統計量,能夠在沒有總體分布先驗信息的情況下,反映出數據在選定樣本X的某一時間段內的聚集程度[18]。樣本分位數對于極值的影響敏感程度較弱,而且在數據預處理方面可以看出樣本分位數克服了異常值點對于分析結果的影響,可有效實現奇異值點的檢測[19]。 通過1.2節對于樣本分位數的定義分析,結合異常值的特點,可得到基于樣本分位數的飛參數據異常值檢測算法,算法步驟為: 步驟1選取飛行過程中實際測量得到的某段飛參數據,共有n個數據點: X=[x1,x2,…xi,…,xn] (1) 步驟2選取時間窗口m=[xi-1,xi,xi+1],其中時間窗口m的選擇結合了樣本分位數的定義及數據分布的內在特性,若窗口選擇過大,此時計算窗口內樣本分位數時會存在對野值點的漏判;若窗口選擇過小,則喪失了統計樣本分位數的意義,因此選擇時間窗口m=3。 步驟3根據選擇的時間窗口m,對飛參數據X進行遍歷,可將原飛參數據X=[x1,x2,…xi,…,xn]轉換為以時間窗口m=3為固定值的多個數據序列片段X′為: X′=[(x1,x2,x3),(x2,x3,x4),… (xi-1,xi,xi+1),…,(xn-2,xn-1,xn)] (2) 步驟4對式(2)中得到的數據序列片段X′中的每個子數據序列進行樣本分位數求解,得到由樣本分位數組成的數據序列為: X″=[q2,…,qi,…,qn-1] (3) 步驟5由于設置的時間窗口m=3,因此公式中的數據長度為n-2。而且由于樣本分位數統計的是樣本之間的整體分布信息,因此可設置閾值,當X′與X″之間差值超過該閾值時,即可認為此處為異常值,并完成對整個數據序列的異常值檢測。 步驟6對于檢測出的異常值xi,采用一階差分法代替該點的異常信息為: (4) 步驟7根據設置時間窗口m=3,運用樣本分位數原理,即可完成對采集到的飛參數據異常值檢測。基于樣本分位數原理的異常值檢測算法流程框圖如圖4。 圖4 算法流程框圖 以某型飛機一個飛行架次中所記錄的飛參數據為例,其中,選取某個階段的某項參數進行分析。受飛行環境的影響,飛參數據中所記錄的該參數存在著噪聲及異常值,所對應的飛參數據數據分布曲線如圖5所示。 圖5 飛參數據分布曲線 如圖5所示,飛參系統記錄的某型參數中的數據有N=100個采樣點,并存在著異常值,這在一定程度上影響了該數據的真實有效性,根據所提出的基于樣本分位數算法,設置時間窗口為m=3,則可以得到98個(N-m+1)寬度為3的由原飛參數據子數據序列組成的時間序列。對這98個時間序列進行50%樣本分位數(也稱為中位數)提取[20]。所得結果曲線如圖6所示。 圖6 基于分位數的數據提取曲線 將圖6中所得的樣本分位數值與原始飛參數據進行差值處理,所得樣本分位數與原始飛參數據之間的誤差值如圖7所示。 圖7 樣本分位數誤差值曲線 如圖7所示,通過對原始飛參數據進行50%的樣本分位數提取之后,野值點處的分位數波動較為明顯,且誤差值較大。因此,可通過樣本分位數提取實現對原始飛參數據的異常值檢測,并實現野值剔除。 根據公式,實現對異常值處的數據修復,經過修復后的飛參數據與原始飛參數據曲線圖如圖8所示。 圖8 異常值檢測結果曲線 如圖8所示,通過設置50%的樣本分位數,可實現對圖5中的三處異常值點的檢測,并根據異常值點修復準則,實現對檢測出的三處異常值點的檢測。 在50%樣本分位數基礎上,采用25%樣本分位數與75%樣本分位數對實驗分析中的飛參數據進行檢測,所得樣本分位數與原始飛參數據之間的誤差值曲線分別如圖9、圖10所示。 對比圖9、圖10與圖7分析可知,25%分位數、75%分位數在三處異常值點的分位數波動較為明顯,且誤差值較大。證明了樣本分位數原理在飛參數據異常值檢測中的合理性;但相比之下,50%分位數具有更直觀更明顯的檢測效果。總體而言,樣本分位數原理僅通過對數據序列進行分析即可完成飛參數據的異常值檢測,具有很好的自適應性與簡潔性。 圖9 25%樣本分位數誤差值曲線 圖10 75%樣本分位數誤差值曲線 1) 通過設置合理的時間窗口,既保留了原始飛參數據序列的數據內部結構,又能準確提取飛參數據異常值處信息。 2) 樣本分位數的選擇,能夠以數據的形式有效檢測飛參數據的異常值,簡單有效,具有實用價值。 3) 通過樣本分位數方法進行異常值檢測,無需獲取數據的內部聯系及先驗信息,僅通過對數據本身進行分析即可得到準確的檢測結果。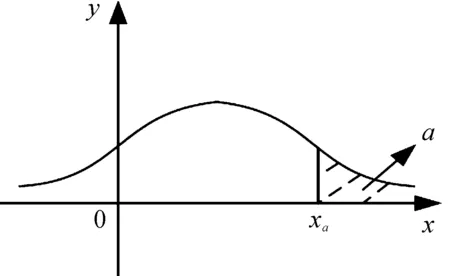

2 算法實現
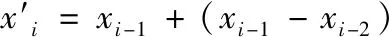
3 仿真與結果分析




4 結論

