彈體壁厚對模擬彈侵徹能力影響分析

王辰瑞，洪 亮

(南京理工大學 能源與動力工程學院，南京 210094)

現代戰爭中，大量的攻擊目標轉入地下或增加了厚重的裝甲，如指揮中心、控制中心、戰艦、裝甲車等，目標打擊難度的增加，對穿甲彈的侵徹能力就提出了更高的要求。穿甲彈依靠動能穿甲，因此彈體質量對于其侵徹能力具有決定性的影響，那么在控制彈體直徑、長度、質量不變的情況下，彈體壁厚的改變對于彈體侵徹能力具有什么樣的影響就需要進一步的討論。

在此前，國內外很多學者已經對戰斗部壁厚對侵徹能力的影響進行了詳細的論證研究，如Forrestal[1-2]小組研究了侵徹彈直徑對其侵徹能力的影響，陳小偉[3]從力學角度給出了彈丸的無量綱壁厚。吳凱等[4]通過改變彈體頭部形狀得到的速度衰減曲線論證了彈體頭部結構對其侵徹性能的影響。李慧卓等[5]論證了彈體結構對混凝土侵徹彈侵徹深度的影響。王金濤等[6]設計了一種彈頭為復合結構的穿甲彈，為彈體結構設計提供了一定的理論依據。呂竹文等[7]針對不同厚度復合裝甲進行了抗穿透性分析，對于穿甲彈侵的設計提供了一定的幫助。

綜上所述，直接以彈體壁厚為變量的分析計算尚顯不足，對彈體壁厚進行分析，增強彈體的侵徹能力，對于未來破壞厚重裝甲的作戰任務是必要的。本文主要利用LS-DYNA軟件對侵徹過程進行仿真，結合現場試驗結果，驗證彈體壁厚對平頭彈侵徹能力影響的變化規律。

1 物理模型及數值仿真

1.1 數值模擬方法與物理模型

數值仿真分析法中的有限元法是研究侵徹問題時使用較多的方法。該方法先將連續求解域離散化為有限個單元，利用計算機通過數值計算方法求得問題的近似解[8-9]。拉格朗日法是彈丸侵徹金屬靶板的常用方法，該網格連接在彈丸和靶板的剛性材料上，隨著彈丸和靶板的侵徹和擠壓，單元網格發生變形。在網格形變量較大時，拉格朗日方法容易產生負體積，導致計算錯誤。

兩種彈芯直徑、長度相同，為保證總質量不變，控制彈體壁厚為變量，通過改變內部塑料假藥密度，調節內部塑料假藥質量，可保證彈體總質量一定。平頭彈體結構如圖1所示，彈體初速度固定為289 m/s，垂直侵徹金屬靶板。本文采用3.6 mm、5.4 mm、6.0 mm、6.6 mm、7.2 mm共五種壁厚模型進行試驗及仿真計算。

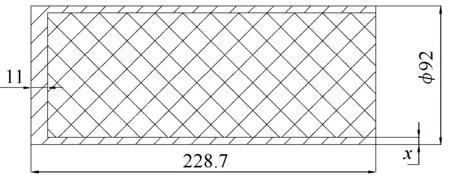
圖1 彈體模型示意圖

1.2 仿真模型

為了減少計算量，加快求解速度，本文沿對稱平面上建立了四分之一模型。利用Solidworks建立三維實體模型，以iges格式導入hypermesh中劃分網格，由于侵徹主要發生于彈丸頭部與靶板的接觸部分，因此對接觸部分的網格進行加密，避免因網格變形嚴重引起的計算錯誤，模型如圖2。

圖2 薄壁彈體1/4有限元模型

將網格文件導入DYNA的前處理軟件Prepost中進行算法及邊界條件設置，將單元類型設置為solid164實體單元。對于不發生侵徹的假藥與彈體外壁之間采用自動的面面接觸算法AUOTOMATIC SURFACE TO SURFACE，針對彈丸與目標的接觸問題，采用面面接觸的侵蝕算法ERODING SURFACE TO SURFACE，在靶板的邊界面上施加非反射邊界條件NON REFLECTING，侵徹接觸控制CONTROL CONTACT的接觸剛度取值為侵徹計算時常用的SLSFAC=0.1。彈體及靶板采用Johnson-cook模型[10]，該模型能很好地模擬金屬材料間的侵徹破壞。

JC本構方程如下：

(1)

其中，無量綱溫度

(2)

斷裂失效由下式定義：

[1+D5T*],EFMIN)

(3)

ρ為密度，G為剪切模量，E為楊氏模量，Pr為泊松比，A為屈服應力參數，B為硬化系數，N為硬化指數，C為應變率系數，M為溫度系數，Tm為熔化溫度，Tr為環境溫度，D1～D5為失效參數。

本文靶板材料采用921A鋼[11]，失效準則參考李繼承等的計算方法，采用最大失效應變作為單元失效準則，取D1=1.13，彈體材料采用30CrMnSi鋼，參數見表1、表2。

2 現場試驗

試驗現場布置如圖3所示，借用高速攝像對出膛后的彈體進行拍攝，觀察彈體飛行姿態及著靶角度等，通過靶板前設置的測速網靶對彈體著靶速度進行估算。

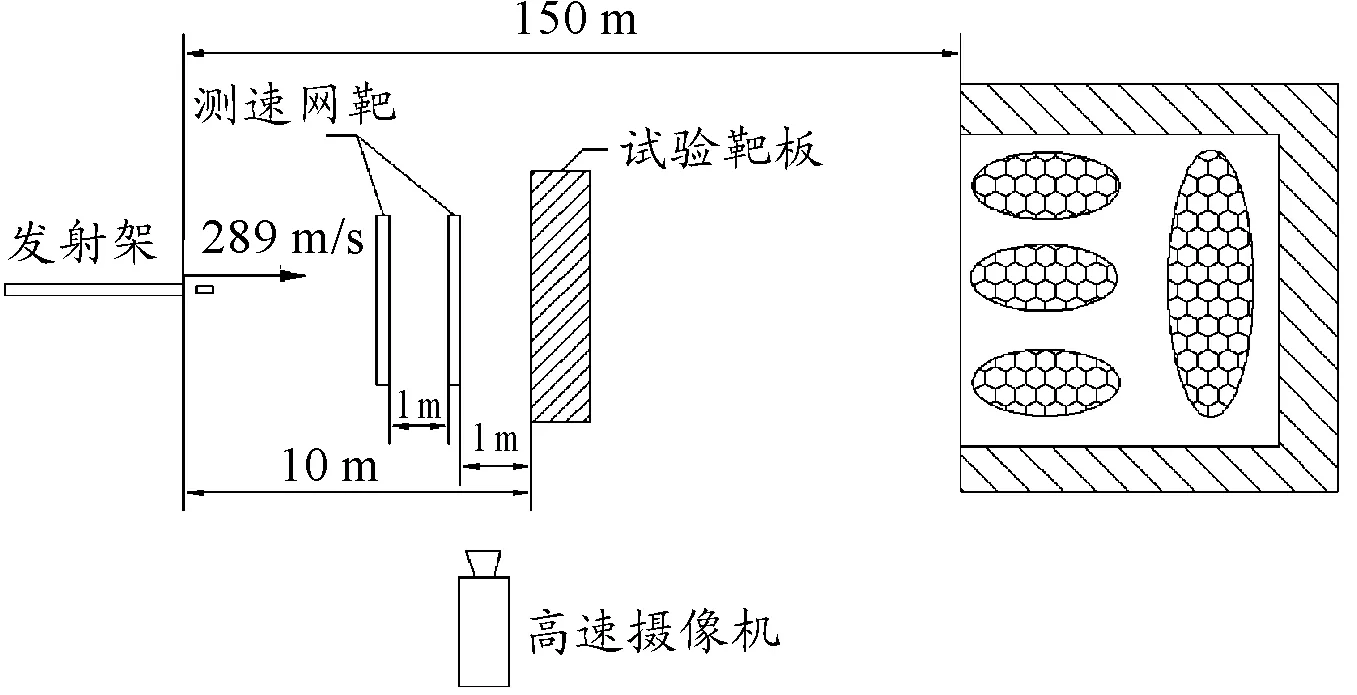
圖3 試驗現場布置示意圖

現場試驗結果如表3，不同彈體速度及不同靶板厚度所得靶板破壞情況不同，可以根據靶板的凹陷深度獲得較為精確的參考數據，與仿真結果進行擬合對比。3號靶板及7號靶板的破壞情況如圖4所示，可見彈體壁厚不足時侵徹效果較弱，在靶板中央撞出圓形凹坑，彈體壁厚增大時擊穿靶板留下圓形穿孔，靶板整體凹陷變形。

表1 靶板材料921A鋼

表2 彈體材料30CrMnSi鋼

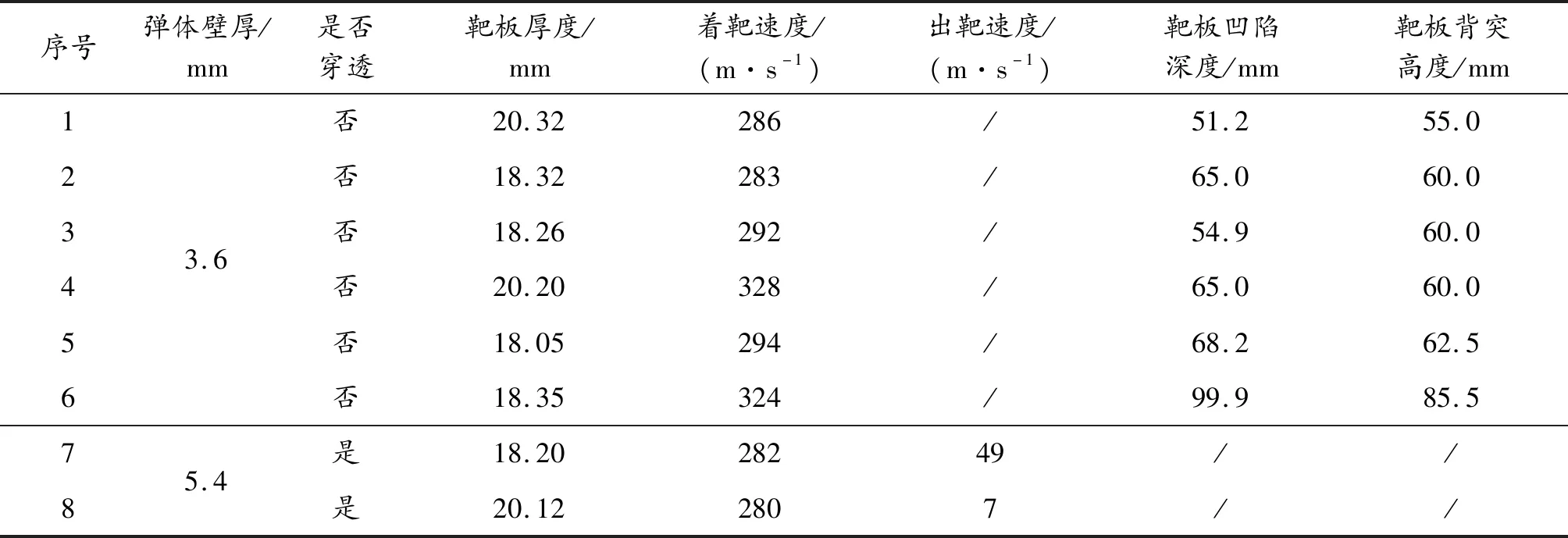
表3 現場試驗情況

3 結果分析

不同壁厚仿真彈芯以289 m/s速度分別侵徹18 mm、20 mm的金屬靶板，仿真結果如圖5所示。

靶板凹陷深度可視為在撞擊結束、靶板震動停止后靶板內側的位移。如圖6所示，3.6 mm壁厚薄壁彈體侵徹靶板的靶板位移曲線可看出，286 m/s初速時靶板凹陷約為54 mm，328 m/s初速時靶板凹陷約為71 mm，兩種情況下的凹陷深度與現場試驗情況的51.2 mm、65 mm基本符合，參考圖7中5.4 mm壁厚彈體的速度曲線，余速分別為10 m/s左右和53 m/s左右，與現場的7 m/s和49 m/s基本符合，因此可認為仿真結果與試驗情況基本符合，材料參數及失效參數可較好的模擬實際情況，擬采用此參數進行下述仿真分析。

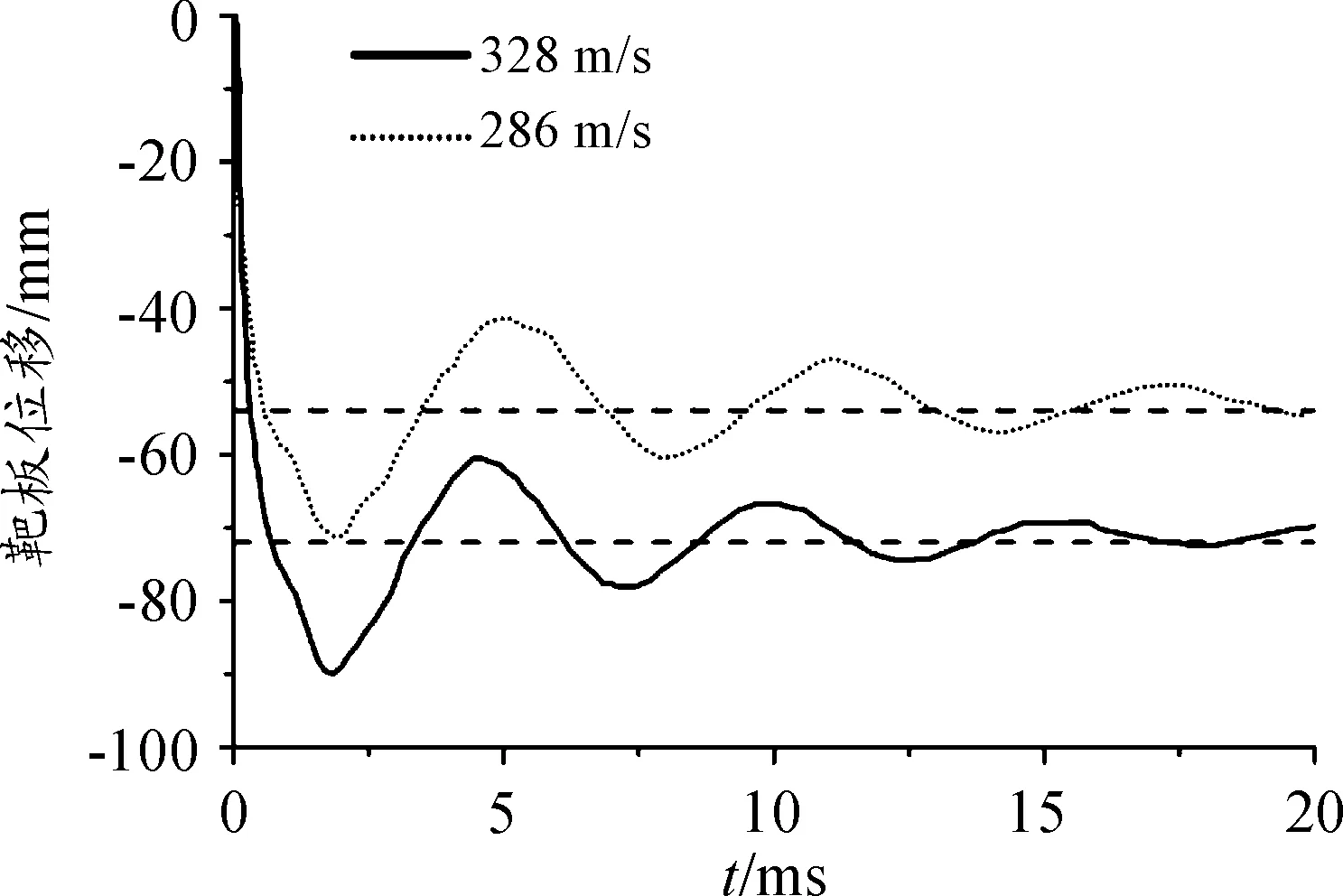
圖6 3.6 mm壁厚彈體侵徹20 mm靶板靶板位移曲線

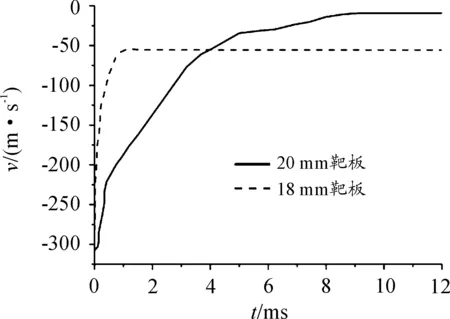
圖7 5.4 mm壁厚彈體侵徹靶板彈體速度曲線

仿真計算得出，不同彈體在侵徹靶板時的速度變化如圖8、圖9所示，從圖中可以看出，總質量相同的彈體，穿透靶板后的剩余速度并不相同，明顯彈體壁厚越厚，剩余速度越高，且速度差幾乎等距，因此對剩余速度和彈體壁厚的關系進行直線擬合，得到結果如圖10所示。

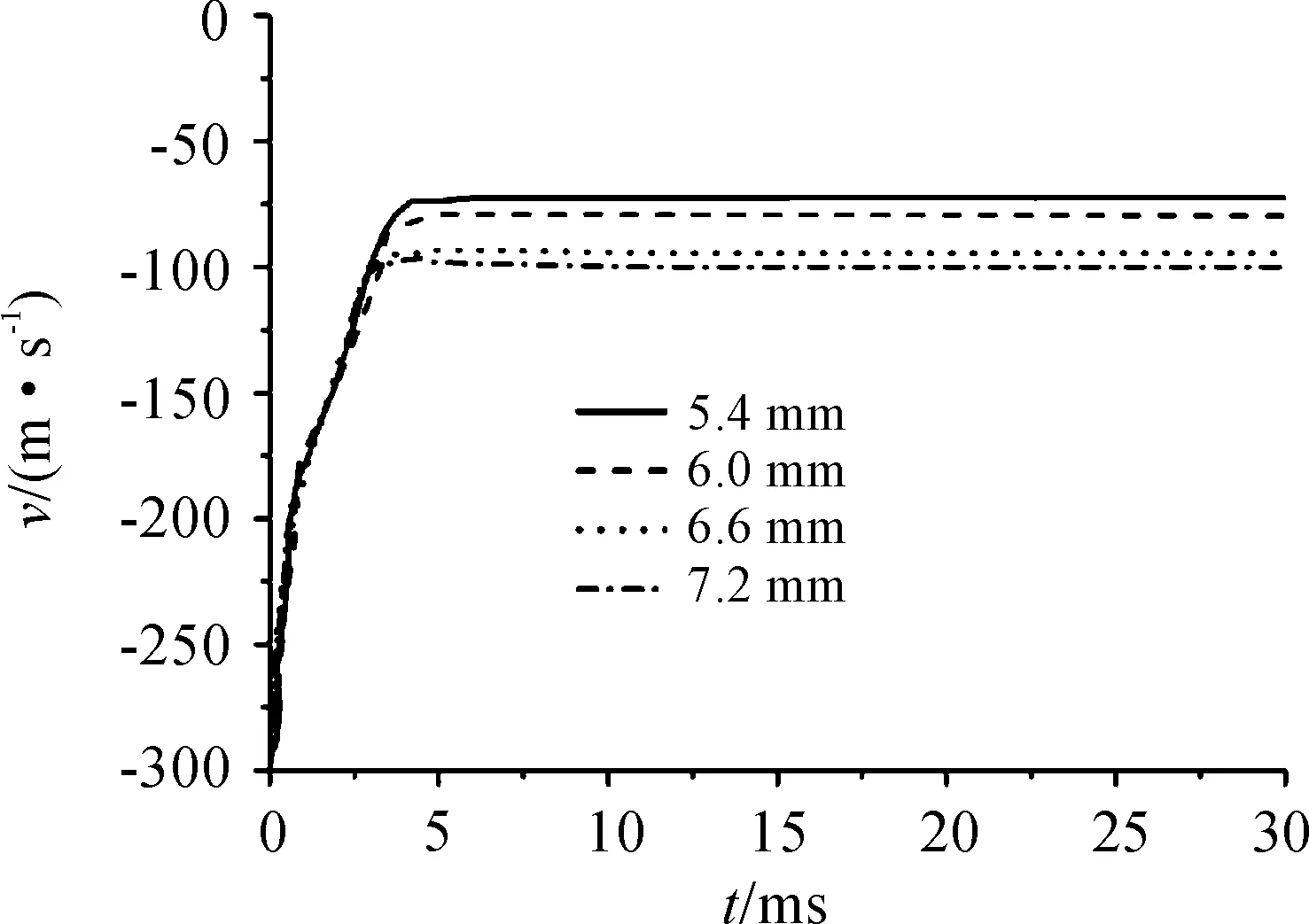
圖8 侵徹18 mm靶板不同壁厚彈體速度曲線

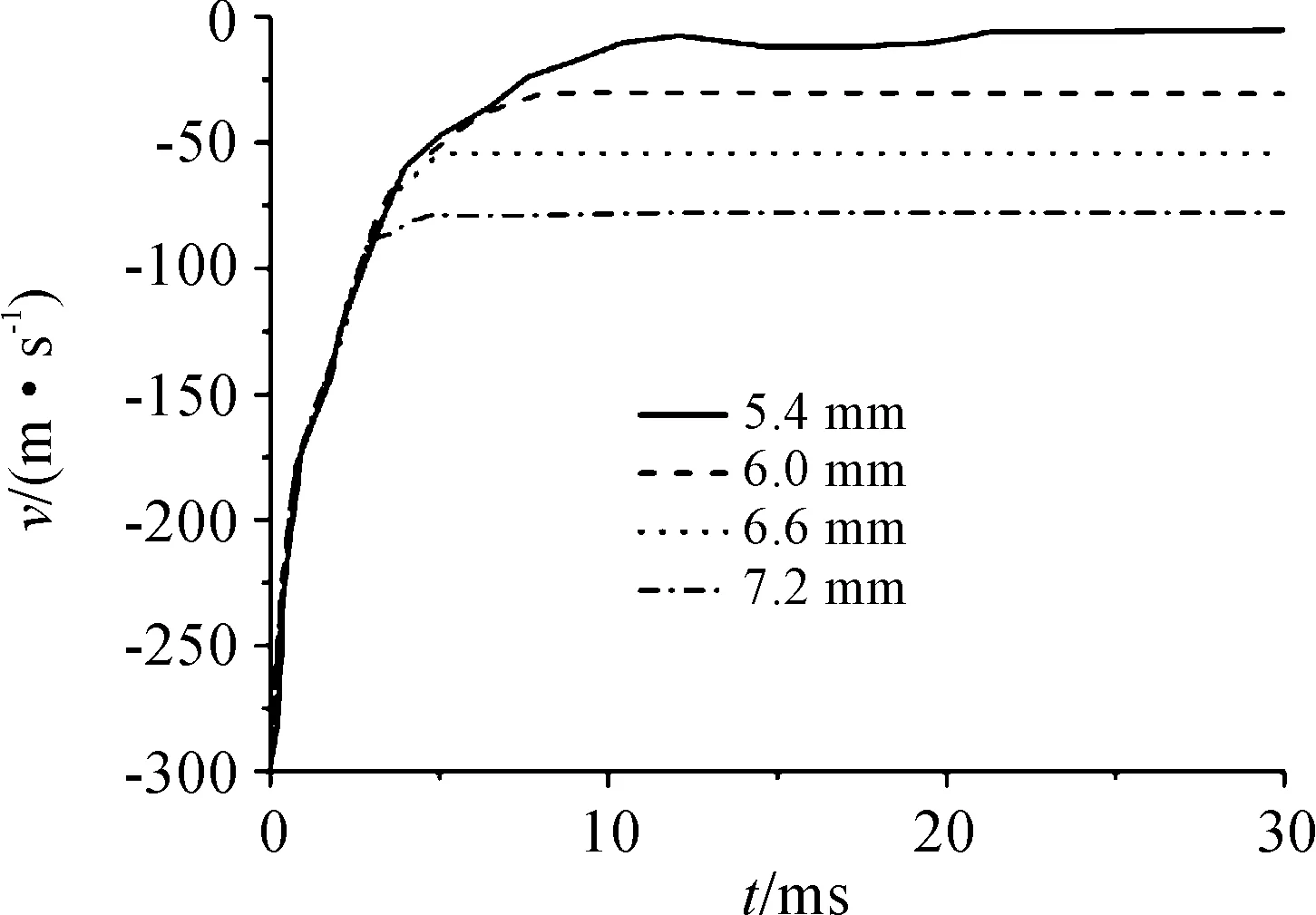
圖9 侵徹20 mm靶板不同壁厚彈體速度曲線

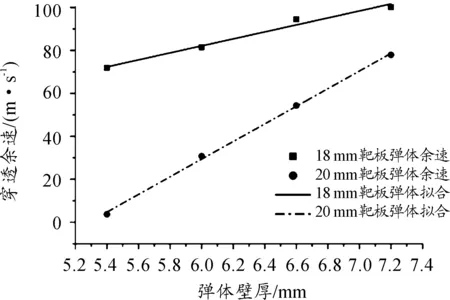
圖10 彈體壁厚-穿透余速擬合曲線

從圖10中可以看出，彈體壁厚與穿透余速之間幾乎成線性相關，彈體壁厚增加，穿透余速也隨之增加，由此可得出，彈體壁厚對于侵徹能力有影響，侵徹能力隨彈體壁厚的增加而線性增長。

4 結論

在控制彈體質量、長度、直徑等變量的情況下，僅改變彈體的金屬壁厚，會對彈體的穿透能力產生影響，彈體壁厚越厚，穿透能力越強。