基于浮動平臺的機器人恒力控制研磨方法

張 鐵，吳圣和，蔡 超

(華南理工大學 機械與汽車工程學院， 廣州 510641)

近年來，工業機器人在金屬加工中的應用越來越廣泛，如打磨[1-2]、拋光[3-4]、去毛刺[5].在這些接觸式工件材料的加工過程中，不僅需要機器人對不同尺寸精度的工件表面有一定的跟蹤性能，還需要保證接觸表面的法向力波動在一定范圍內，以維持恒定的金屬去除率[6]，從而提高表面加工質量.為了使機器人在與未知環境接觸時具有一定的順從能力，國內外已有大量學者做了相關研究，提出機器人的柔順控制，主要包括被動柔順和主動柔順.Huang等[7]研制了一個機器人打磨拋光系統，即在砂帶輪處增加一個彈簧阻尼柔順機構，結合刀具軌跡生成實現渦輪葉片的被動柔順控制打磨.但由于柔順裝置適應能力差，應用范圍受限制，且被動柔順的控制精度取決于柔順裝置，具有力反饋的主動柔順控制逐漸成為研究主流.Jung等[8]針對機器人動力學模型和環境剛度的不確定性，提出自適應增益的阻抗控制器，在環境剛度發生變化時實現機械臂的恒力跟蹤.Zhang等[9]提出一種基于速度伺服的力/位混合控制方法，同時執行穩定的力控制和精確的位置控制，用于機器人的曲面打磨.Marchal等[10]采用迭代學習控制進行機器人的銑削加工實驗，通過迭代學習修正誤差以提高控制精度，能夠減少機器人銑削加工中的位置誤差.Tao等[11]在機器人去毛刺的過程中提出一種模糊比例積分微分(PID)控制方法，通過模糊規則在線更新PID參數，以保證末端執行器的加工軌跡精度.Zhang等[12]針對機器人的跟蹤控制問題，使用徑向基函數神經網絡設計了一個控制器，并引入Lyapunov函數證明了閉環系統的穩定性.但這些控制方法均存在難以確定控制邊界條件、適應能力有限等局限性.

在機器人的金屬加工過程中，切削力的動態變化對控制精度影響較大，有少量學者對機器人加工過程的切削力模型進行了討論.Elbestawi等[13]分析了打磨過程中切削力與金屬去除率的關系，建立了機器人末端安裝氣動打磨機的磨盤磨損模型，提出了廣義預測控制器，在打磨焊珠實驗過程中實現了恒力控制.S?rnmo等[14]則建立了機器人銑削加工模型，針對機器人剛度不足的問題加入了剛度前饋補償，提出基于模型的自適應力控制器并實現恒力控制.Song等[15]在機器人砂帶打磨系統中引入機器學習的智能算法，以歷史磨削樣本作為訓練數據，利用支持向量回歸算法建立機器人砂帶打磨模型，證實了能在力/位混合控制中更好地控制材料去除率.

由于研磨力的非線性變化對機器人研磨的加工精度影響較大，而傳統的PID控制并不能滿足非線性系統的要求，韓京清[16]提出自抗擾控制技術，并逐漸應用于機器人的運動控制上，如機器人路徑跟蹤[17].本文將自抗擾控制技術應用于機器人研磨系統的力反饋控制中.首先提出浮動平臺的機器人研磨系統，對系統的研磨力模型進行了分析，設計了線性擴張狀態觀測器估計輸出狀態總擾動；然后獲得狀態誤差反饋控制律，通過狀態反饋補償方法以減少狀態誤差，實現浮動平臺的機器人恒力研磨控制.本實驗只針對穩定研磨階段，采用離線加載的方式，并離線調整各算法參數，簡化了實驗過程.

1 浮動平臺的機器人研磨系統

1.1 浮動平臺的機器人研磨結構

所設計的機器人浮動平臺研磨結構如圖1所示，由伺服電動機連接直線模組，控制直線模組中滑臺的上下移動，而浮動滑臺上裝有研磨裝置，包括研磨電動機和研磨盤，由工控機發送脈沖信號到伺服電動機控制研磨盤移動控制研磨進給量，而一維力傳感器測量并反饋力信號給工控機以實現閉環恒力研磨控制.

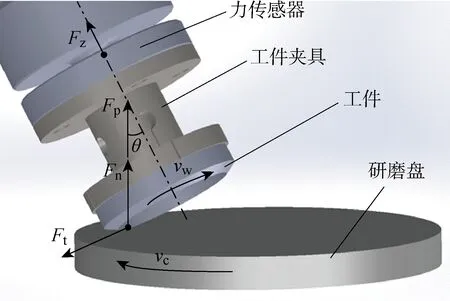
圖2 機器人研磨受力分析Fig.2 Force analysis of robot grinding

1.2 浮動平臺的機器人研磨模型

浮動平臺的機器人研磨模型由兩部分組成，一是機器人末端與未知環境接觸的動力學模型，二是穩定研磨過程中的動態切削模型.研磨過程中的受力關系如圖2所示，其中：vw為工件旋轉線速度；vc為研磨盤旋轉線速度.根據Zhu等[18]關于砂帶打磨受力的研究結論，切向力與法向力所成的比例關系f=Ft/Fn，在圓錐面工件研磨過程中工件所受切向方向的研磨力Ft與一維力傳感器受力Fz所成的夾角為90°，則Ft在Fz方向上的耦合作用可不考慮，研磨盤法向合力F投影到Fz可表示為

Fz=Fcosθ=(Fp+Fn)cosθ

(1)

根據Mendes等[19]的研究，將機器人與環境接觸模型看作一個質量彈簧阻尼器，則可以獲得機器人末端與環境接觸的動力學模型：

(2)

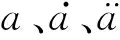
浮動平臺的機器人研磨過程不僅有機器人與環境的接觸，還存在動態磨削.假設研磨盤中單個磨粒的作用類似于單點切削刀具在車削中的作用[20]，則單個磨粒受力主要由切削變形力Fec和滑動摩擦力Fes組成，分別將切削變形力Fec分解為法向力Fenc和切向力Fetc，將滑動摩擦力Fes分解為法向力Fens和切向力Fets，如圖3所示.而單個磨粒的法向研磨力Fen由Fenc和Fens組成：

Fen=Fenc+Fens

(3)

1.2.1切削變形力 由金屬切削變形力可知，單個磨粒的切削變形力的法向力是未變形切削橫截面積的函數，可以得到

Fenc=K1Qi

(4)

每單位磨削寬度的總法向切削變形力為

Fnc=K1∑Qi

(5)

式中：K1為與磨粒參數相關的常系數；Qi為單位磨削寬度上同時作用的各磨粒所對應切屑橫截面積，則有

(6)

代入式(5)可得到

(7)

1.2.2滑動摩擦力 研磨中的摩擦現象是磨損中的磨粒和工件材料之間的摩擦，有實驗證明每個磨粒的法向力將隨著磨損磨粒的接觸面積而發生變化.故單個磨粒法向摩擦力為

(8)

(9)

式中：N為參與摩擦磨粒的總數.應用Werner[21]關于嚙合切削刃數的公式，N可以寫成

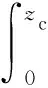
(10)

式中：α和β分別為切削刃分布的指數系數；Nydn為不同單位長度參與研磨的磨粒數量；zc為磨粒與工件的接觸長度；ds為研磨盤研磨直徑；ON為比例系數；ρ1為切削刃密度.

將式(10)代入式(9)可獲得總法向摩擦力

(11)

式中：K2為與砂粒工件接觸的平均面積、平均接觸壓力等因素相關的常數.

由式(7)和(11)可得單位磨削寬度磨粒總法向力為

(12)

由式(2)和(12)可得浮動平臺的機器人法向研磨合力為

F=

(13)

2 機器人自抗擾控制研磨算法

2.1 擴張狀態觀測器的設計

擴張狀態觀測器用于觀測系統輸出狀態變量及估計系統外部干擾，并做出補償.由式(13)可得單輸入、單輸出的機器人浮動平臺研磨非線性系統模型，同時考慮研磨過程中的時變因素w(t)可得

(14)

以u表示系統輸入，y(t)表示系統輸出，將式(14)簡化為一般的標準形式，

(15)

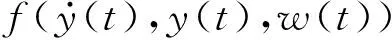
(16)

式中：狀態矢量x=[x1x2x3]T∈R3.式(16)中的狀態方程部分可寫成如下矩陣形式：

(17)

對式(17)設計如下線性擴張狀態觀測器[22]：

(18)

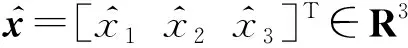
由式(17)和(18)得

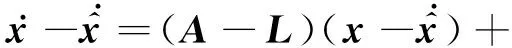
(19)

式(19)中矩陣(A-L)的特征方程為

|λI-(A-L)|=λ3+l1λ2+l2λ+l3

(20)

(21)

那么式(19)的特征式為

|λI-(A-L)|=(λ+w0)3

(22)

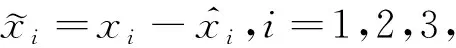
(23)

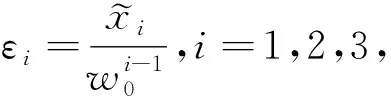
(24)

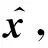
證明因為A′是Hurwitz矩陣，則存在一個唯一的正定矩陣P滿足A′TP+PA′=-I，選擇Lyapunov函數為：V(ε)=εTPε，因此

(25)

(26)

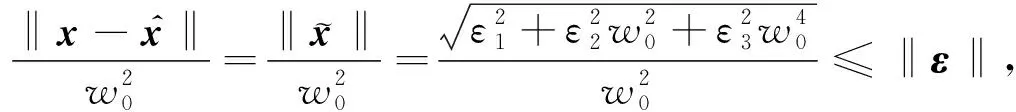
(27)

式中：c′=2‖PB′c‖，由式(25)和(27)可得

(28)

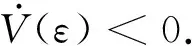
由定理1可知，式(18)擴張狀態觀測器的觀測誤差是收斂的.

2.2 閉環穩定性分析

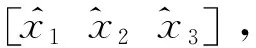
(29)

式中：k1>0,k2>0為控制器參數；r為有界輸入.將式(29)代入式(15)得

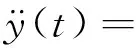
(30)

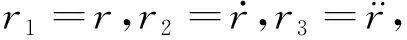
(31)

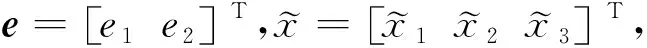
(32)

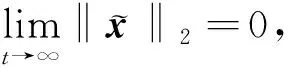
證明：式(32)的解為

e(t)=

(33)

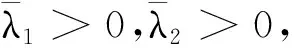
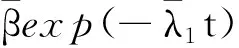
(34)

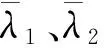
(35)

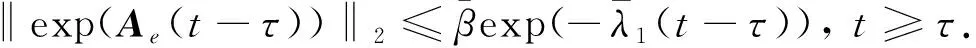
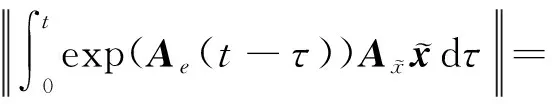
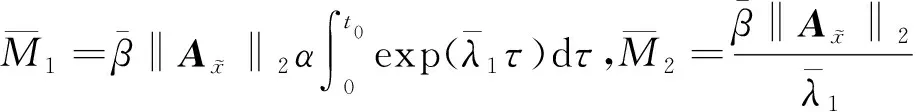
(36)

因此，由定理2可以得到所設計的反饋控制律即式(29)，是閉環穩定的.

2.3 線性自抗擾(LADRC)控制離散算法

由式(18)設計的擴張狀態觀測器，以及式(29)設計的反饋控制律，同時引入由最速綜合函數提供微分信號的過渡過程，得出如下線性自抗擾控制離散控制算法.

(1) 過渡過程(TD)離散算法

(37)

式中：th為系統的采樣時間常數；Fd為系統期望力；v0為系統的響應速度；q0為濾波因子；Z為一個常整數；函數fhan(t1,t2,r0,q0)為最速綜合函數，具體表達式為

fhan(t1,t2,v0,q0)=

(38)

(39)

(40)

(2) 線性擴張狀態觀測器(LESO)的離散算法

(41)

式中：y(k)、u(k)為線性擴張狀態觀測器的輸入；eLESO為線性擴張狀態觀測器的觀測誤差.

(3) 狀態誤差反饋(LSEF)的離散算法

(42)

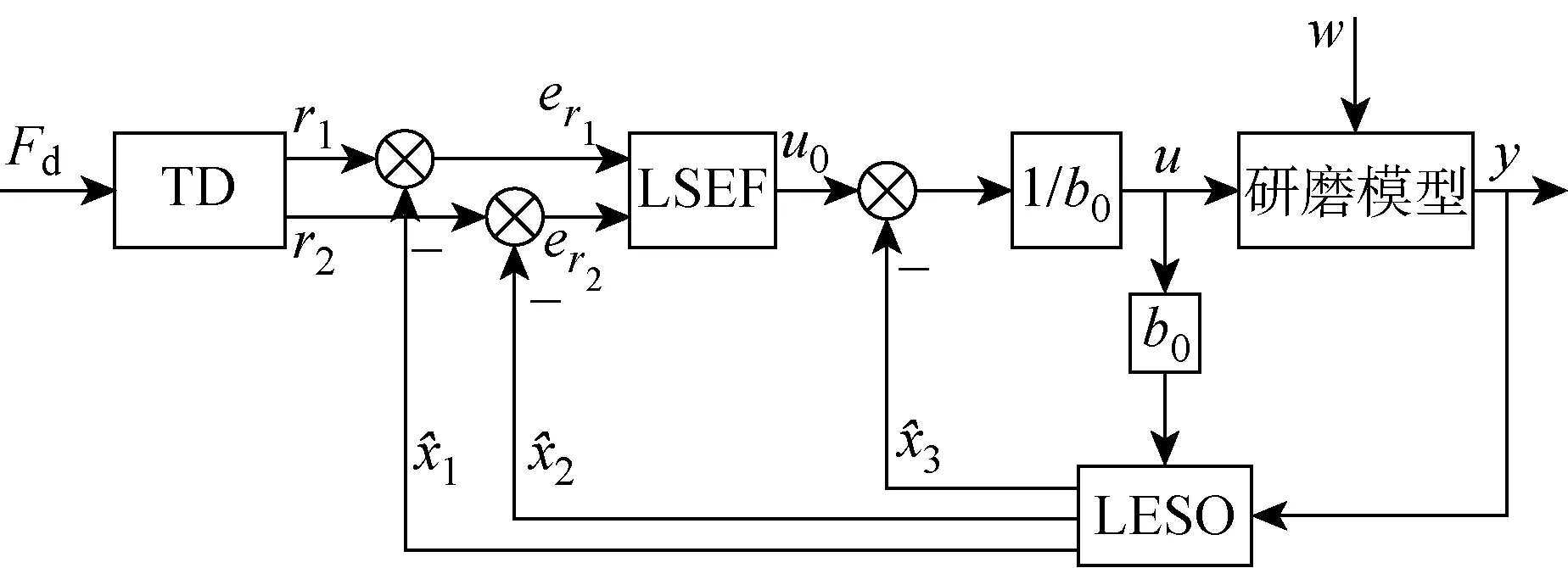
圖4 浮動平臺的機器人線性自抗擾研磨算法Fig.4 Linear active disturbance rejection control for robot grinding on floating platform

3 浮動平臺的機器人力控制研磨實驗

3.1 研磨實驗裝置

由于機器人的定位精度差，為了實現更高的控制精度，采用的是浮動研磨平臺的控制方案.實驗裝置如圖5所示，采用UR5機器人.實驗中機器人運行示教好的運動軌跡，使工件待研磨面不斷進入研磨盤的研磨區域.一維力傳感器將 -10～10 V的電壓模擬信號輸入到倍福EK1100耦合器，轉化為數字信號發送給工控機實時系統處理，再將脈沖數字量發送給伺服驅動器控制交流伺服電動機運動，經直線模組使研磨盤產生位置偏移量，實現閉環恒力研磨控制.浮動平臺的機器人研磨系統結構如圖6所示.

圖5 機器人研磨實驗裝置Fig.5 Robotic grinding experiment device

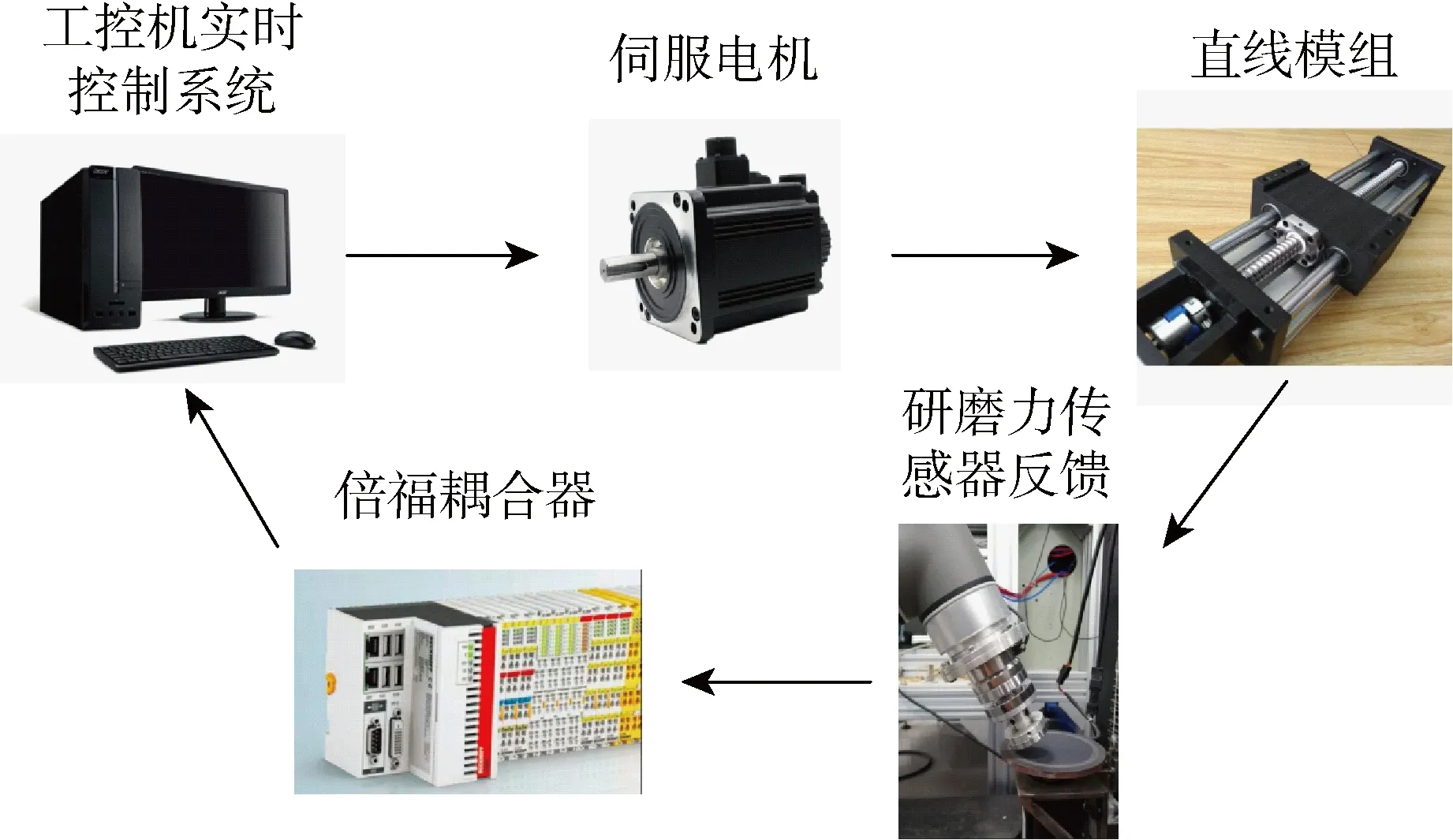
圖6 機器人研磨控制系統結構Fig.6 Structure of robotic grinding control system

3.2 研磨實驗結果

為了驗證線性自抗擾控制算法在浮動平臺的機器人研磨控制中的有效性，分別進行了開環控制研磨實驗、PID控制研磨實驗、線性自抗擾控制研磨實驗.實驗工件材料為45號鋼，圓錐面工件，法向期望力設置為5 N，vc=1 115 mm/s，vw=3.5 mm/s.每次當實驗研磨盤與工件研磨力達到5 N后，工件進行旋轉，研磨盤開始執行控制算法.開環控制的研磨實驗如圖7所示.

由圖7可知，由于在機器人軌跡運行過程中，工件表面輪廓存在不規則的加工誤差，同時又沒有浮動平臺對機器人研磨力的變化進行研磨盤位移調整，所以傳感器獲得的力信號也呈現不規則變化，使得開環控制不能實現恒力控制.

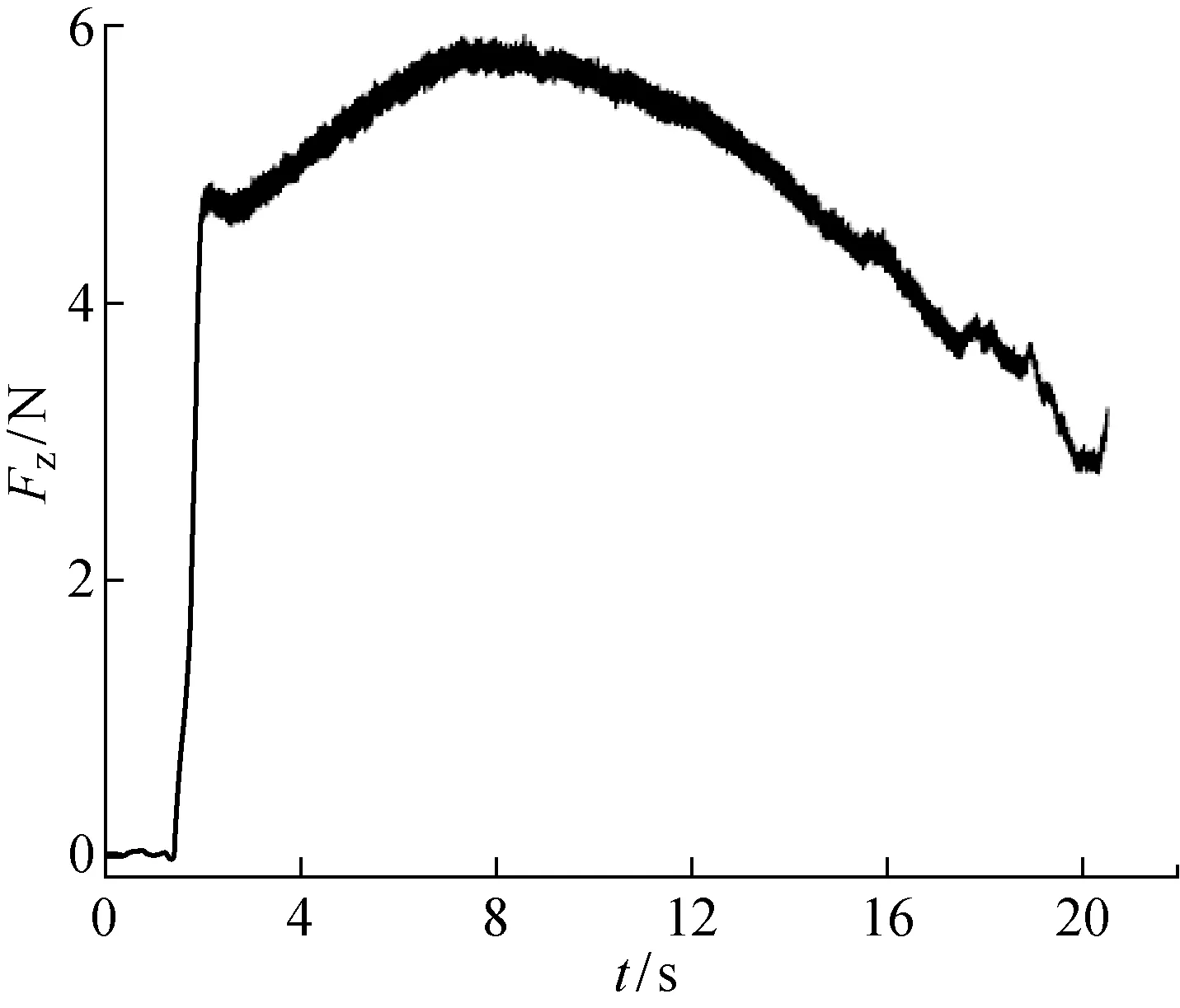
圖7 開環控制研磨實驗Fig.7 Open loop control grinding experiment

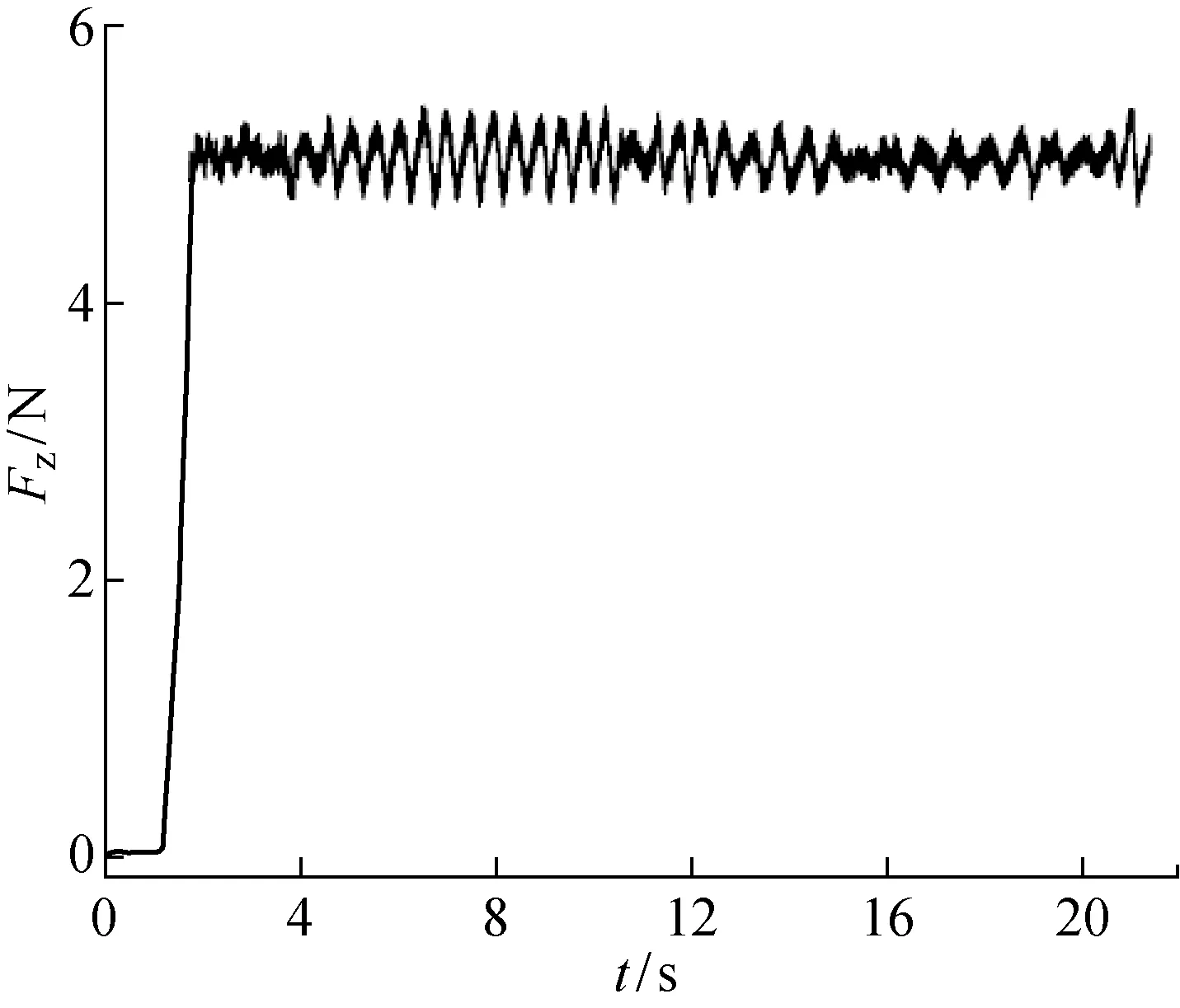
圖8 PID控制研磨實驗Fig.8 PID control grinding experiment

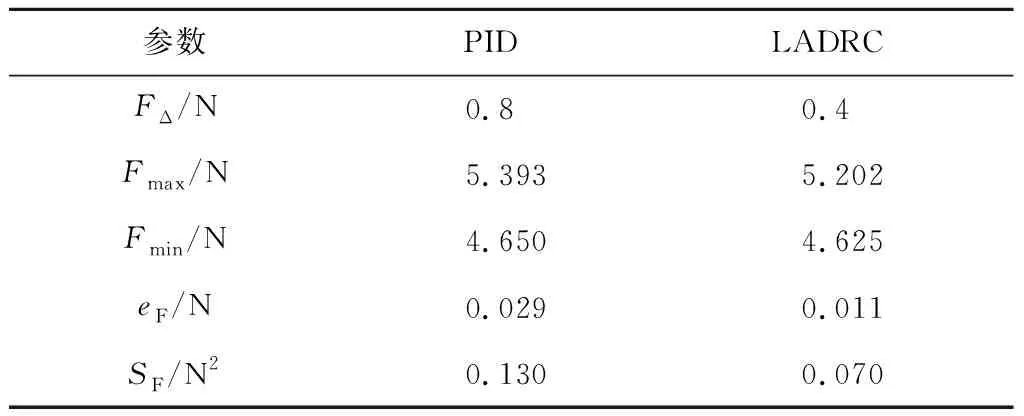
為了保持恒定的研磨力，需要維持一定的金屬去除率，并進行浮動平臺的力反饋PID控制，其中PID控制參數根據經驗經過多次調整，先對各參數進行粗調整，而后再作微調整，調整后獲得的最優參數為Kp=45，KI=0.03，KD=0.15.PID控制研磨的實驗結果如圖8所示.在穩定研磨狀態下的力波動為0.8 N，最大研磨力Fmax=5.393 N，最小研磨力Fmin=4.650 N，研磨力平均誤差eF=0.029 N，研磨力方差SF=0.130 N2.結果表明：PID控制雖然能保持恒定的研磨力，但研磨力控制精度難以滿足要求，力的變化不穩定.

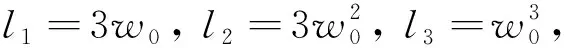
線性自抗擾控制器參數調整結果如表1所示.

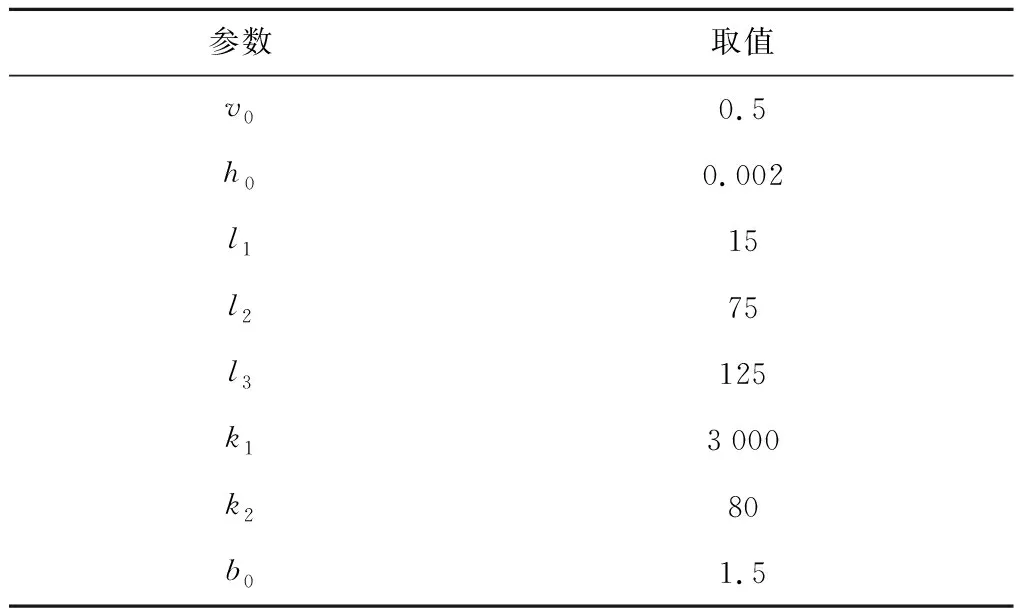
表1 LADRC控制參數Tab.1 Control parameters of LADRC

線性自抗擾研磨實驗結果如圖9所示.由圖9可知，由于式(37)最速綜合函數安排的過渡過程，剛開始有一段緩慢進入穩定研磨狀態的過程，穩定研磨下狀態力波動FΔ=0.4 N，Fmax=5.202 N，Fmin=4.625 N，eF=0.011 N，SF=0.070 N2.PID控制和線性自抗擾實驗測量結果數據如表2所示. 對比PID實驗結果可以看出，線性自抗擾控制算法能顯著地減少穩定研磨狀態下的力波動，研磨力平均誤差也減少，可以提高浮動平臺穩定研磨的控制效果.

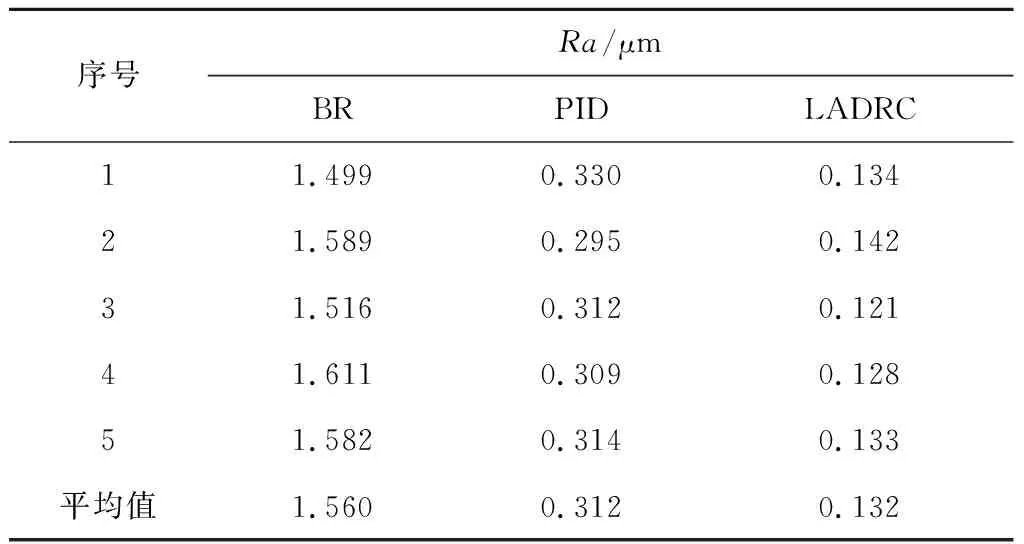
研磨前后的工件如圖10所示，采用時代之峰的TIME 3202粗糙度儀檢測表面粗糙度，分別測量工件的不同位置表面粗糙度各5次如表3所示， 其中BR表示研磨前.研磨前的平均表面粗糙度Ra=1.560 μm；PID恒力研磨控制過程力的變化比較大，且金屬去除率不穩定，影響了工件表面加工質量.因此，經過PID恒力研磨控制平均表面粗糙度Ra=0.312 μm； 而線性自抗擾控制相較于PID控制法的研磨法向力更穩定，使得平均表面粗糙度降低到了Ra=0.132 μm，從而大大地提高了工件表面的加工質量.

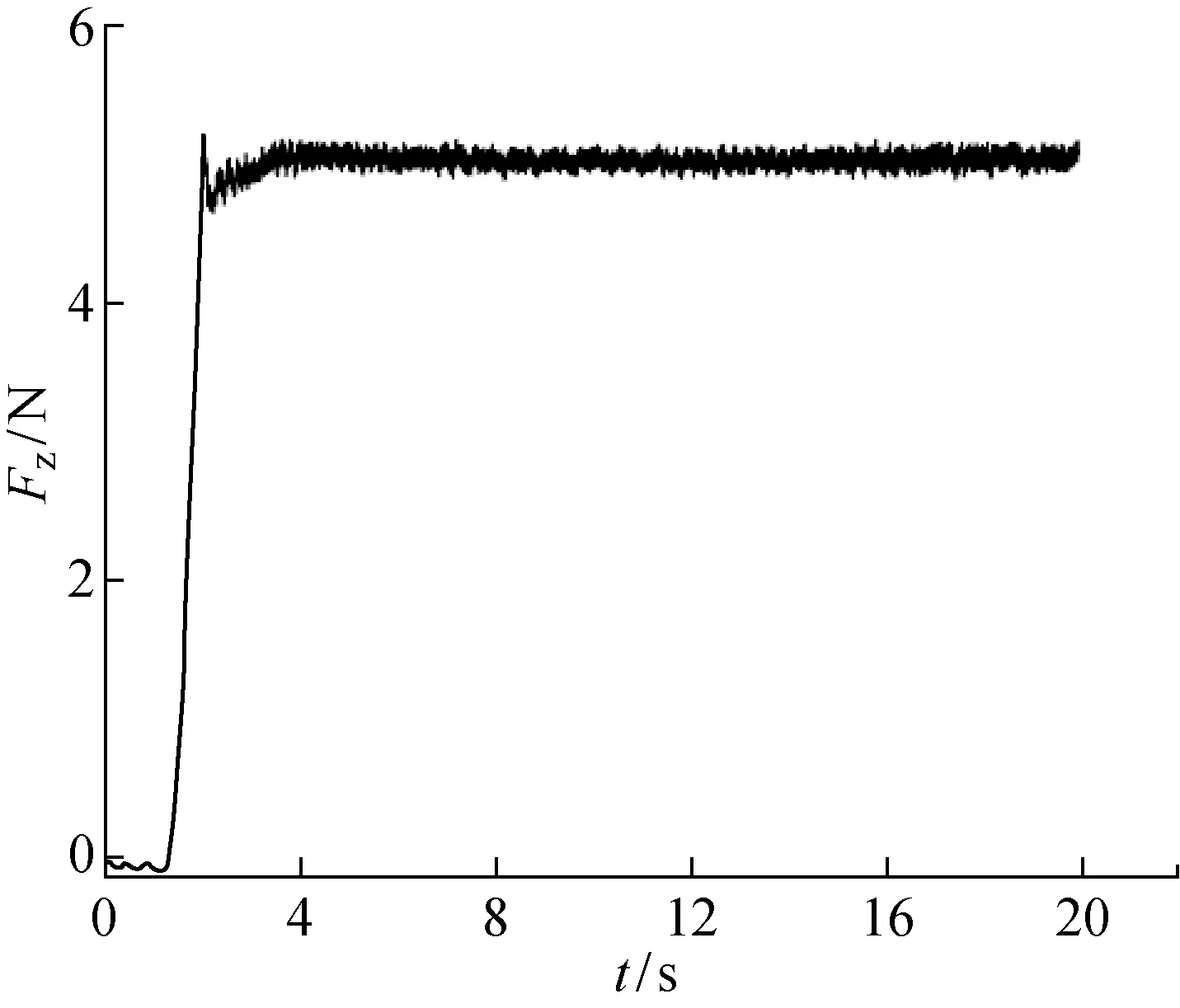
圖9 LADRC研磨實驗Fig.9 LADRC grinding experiment

參數PIDLADRCFΔ/N0.80.4Fmax/N5.3935.202Fmin/N4.6504.625eF/N0.0290.011SF/N20.1300.070

圖10 研磨工件對比Fig.10 Comparison of grinding workpieces

序號Ra/μmBRPIDLADRC11.4990.3300.13421.5890.2950.14231.5160.3120.12141.6110.3090.12851.5820.3140.133平均值1.5600.3120.132

4 結語

針對機器人在研磨過程中的控制精度不足問題，研制了浮動平臺的機器人研磨系統，采用一維力傳感器實現力反饋控制.對機器人末端圓錐面工件表面進行受力分析，結合機器人與未知環境接觸的動力學和研磨盤法向受力模型，構建了機器人浮動平臺的研磨力模型.

根據所提出的浮動平臺的機器人研磨模型，設計了能夠估計狀態輸出的線性擴張狀態觀測器，并檢驗了線性擴張狀態觀測器的估計能力，利用線性擴張狀態觀測器的輸出設計線性狀態誤差反饋控制律，構建Lyapunov能量函數證明了閉環穩定性，得出了浮動平臺的機器人線性自抗擾研磨算法.

通過圓錐面工件的研磨實驗驗證浮動平臺的機器人線性自抗擾研磨算法的有效性.實驗結果表明：線性自抗擾算法可以實現浮動平臺的機器人研磨力有效控制；與傳統的PID控制相比，研磨力控制誤差減少了61%，研磨力方差減少了47%，研磨力的穩定性提高了50%，實驗工件的平均表面粗糙度降低了0.180 μm.因此所提出的浮動平臺的機器人線性自抗擾研磨算法能夠滿足高精度零件表面的研磨.