圖示表征在第二學段倍比問題中運用策略研究

鄔旭亮

【摘?要】“倍比”問題是具有典型意義的一類數學問題。在學習過程中發現，無論是三年級簡單的倍數關系還是五六年級較為復雜的“和倍關系”、“差倍關系”，學生解決此類問題的錯誤率高居不下。

【關鍵詞】圖示表;策略;研究

“倍比”問題是具有典型意義的一類數學問題。在學習過程中發現，無論是三年級簡單的倍數關系還是五六年級較為復雜的“和倍關系”、“差倍關系”，學生解決此類問題的錯誤率高居不下。

到底是什么原因造成了這個問題呢？我們覺得教材編排中有兩個問題值得我們教師考慮：

一、潛入潛出，弱化倍比問題

或許潛入淺出弱化倍比問題才是教材編排的本意。三年級上冊才正面呈現倍比問題，而且呈現的都是常規的“誰是誰的幾倍？誰比誰多（少）幾倍？”到練習十一時的兩個拓展練習隱約看到了“幾倍多（少）幾？”的影子。六年級上冊也是如此。而五年級上冊除了在小數乘法中有所涉及外，還出現在實際問題與方程這個內容中，而這個內容本身就有知識點的局限性。這樣一來，倍比問題確實得到了弱化，但我們的配套練習卻不是這等水平。

二、重圖示表征，輕畫圖技能

新課標（2011版）數學核心概念相比與實驗稿新增了運算能力、模型思想、幾何直觀、創新意識，因此我們的教材也隨之變化。教材中運用的圖示表征就大量增加。我們梳理后發現小學階段涉及到倍比問題的內容都有圖示表征，但有個問題我們也不能忽略。教材中安排的圖示表征都是學生被動接受的，學生打開書本就看到完整的圖，學生并不懂畫的方法。因為學生只看到了結果并沒有經歷“抽象——直觀”這樣一個完整的過程。

那么我們怎么做才能讓學生在倍比問題中主動運用圖示表征呢？我覺得可以從以下度進行嘗試：

三、以圖示意，讓學生感受畫圖

學生圖示表征的幾何直觀能力培養不是說來就來的，它是從始至終慢慢形成的。在第一學段，學生受認識水平的困擾無法大量的識字，所以看文知意就難為我們的學生了。在這種情況下我們就要引導學生畫一畫，圈一圈，將抽象的文字用直觀的形式表達出來。

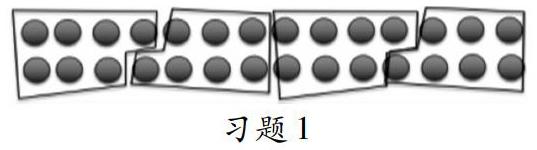
如：習題1：28個桔子，7個裝一袋，可以裝幾袋？9個裝一袋又可以裝幾袋？

初遇這個問題時學生不知道怎么辦？即便照著寫28-7-7-7-7=0學生也不一定明白等式上的答案是0，為什么口答時要說4袋呢？這時我們的老師可以少說，引導學生通過畫一畫、圈一圈的方式去找答案。

通過讓學生經歷這樣的以圖示意過程后，學生就能深刻感受到運用圖示表征能將復雜問題直觀化，在解決學習困難的同時也體會到圖示表征帶來的優越性。

四、對比優化，讓學生感知畫圖

在新課標修訂后，數學核心素養有所變化，增加了幾何直觀、創新思維等幾個核心概念，我們的教材也加大了圖示表征在學習過程中的作用。所以對那些無法用語言來表述解題思維以及無法理解他人表述解題思維的學生來說一個極好的輔助。但初嘗圖示表征優越性之后學生并沒有掌握一定的圖示表征技能，他們并未感知真正的畫圖，所以教師要在教學中不斷的對比優化，讓學生感知畫圖。

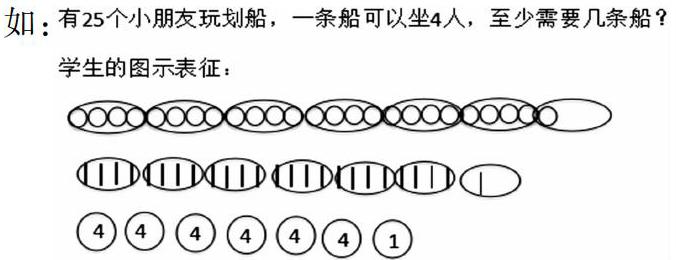
如：

以上3種圖示表征都正確表述了解題思路，教師完全可以在此基礎上從圖示的簡介、效率等方面引導學生進行優劣對比，進而讓學生感知數學中的數學中圖示表征的運用要的是言簡意賅，畫出主要特征就行。

五、點播提升，讓學生感悟畫圖

在學生經歷了感知圖示表征后只是進入了圖示表征的初級階段。讓學生能采用合理的圖示來表征數量關系才能真正感悟到圖示表征“抽象——直觀——抽象”的強大作用。

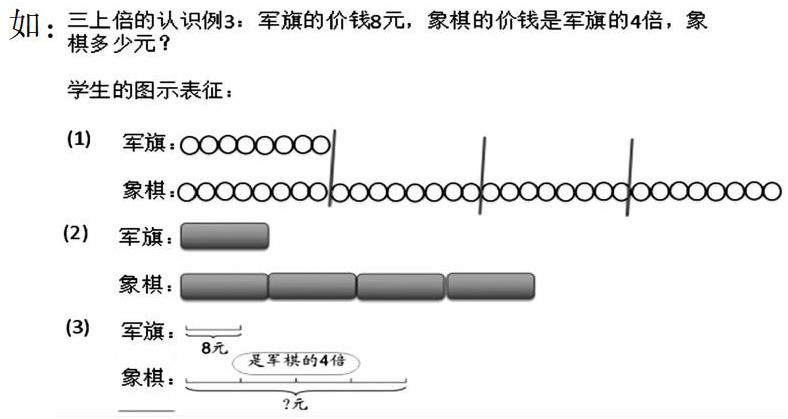
如：

上圖中學生通過利用已有的圖示表征經驗將抽象的文字進行了直觀轉化，。圖中（1）的轉化是圖示表征的初級水平，它是線段圖原始形態，用具體的符號一一對應實體，雖然也用到了符號，但卻離不開一一對應，說明該生的水平還有待提高;圖中（2）的轉化是圖示表征的中級水平，雖然也是用符號代替實體，但明顯已經拋卻了一一對應，說明他已經有了將具體物抽象成符號的意識，反射出“抽象——直觀——抽象”的影子，只不過還有待改進;圖中（3）的轉化就完全是圖示表征的最高水平，不但體現了“抽象——直觀——抽象”的過程，還清楚的表示出了數量關系，讓人一目了然。所以我們要借機對三種圖示表征進行聯系溝通，讓（1）（2）兩種轉化的同學在溝通中受到點播從而完善他們圖示表征的幾何直觀能力。

隨著圖示表征運用的增多，你就會發現它在倍比問題中的作用越大。因為它能將阻擋在學生面前的迷霧吹得清晰，所以我們要堅持讓學生受益下去，讓他們的數學能力越來越強。