基于離散伴隨方程的三維雷達(dá)散射截面幾何敏感度計(jì)算

周琳，黃江濤，高正紅,*

1. 西北工業(yè)大學(xué) 航空學(xué)院，西安 710072 2. 中國空氣動(dòng)力研究與發(fā)展中心，綿陽 621000

雷達(dá)散射截面(Radar Cross Section, RCS)反映了物體在給定方向上對入射雷達(dá)波散射的強(qiáng)弱，是衡量飛機(jī)隱身性能的重要指標(biāo),考慮隱身的飛行器設(shè)計(jì)常以減小雷達(dá)散射截面作為隱身設(shè)計(jì)的重要目標(biāo)。現(xiàn)有飛行器隱身設(shè)計(jì)中多采用幾何光學(xué)法(GO)、物理光學(xué)法(PO)、幾何繞射理論(GTD)、物理繞射理論(PDT)等高頻近似算法評(píng)估散射體的雷達(dá)散射截面[1-2]。高頻算法根據(jù)高頻場的局部性原理，僅根據(jù)入射場獨(dú)立地近似確定表面感應(yīng)電流[3]，計(jì)算速度快，所需內(nèi)存小。近年來，隨著反隱身技術(shù)的發(fā)展，尤其是全數(shù)字化有源相控技術(shù)在低空警戒和監(jiān)視雷達(dá)中的應(yīng)用，對飛行器隱身性能的要求越來越高[4]。高頻方法雖然可以預(yù)估飛行器目標(biāo)的鏡面散射、邊緣繞射等散射特性，但由于算法本身的局限，忽略了一些關(guān)鍵部件間的耦合關(guān)系，在弱散射源計(jì)算中的精度不足，使其在低RCS構(gòu)型的評(píng)估和優(yōu)化過程中可信度較低，無法滿足低RCS構(gòu)型精細(xì)化設(shè)計(jì)的需求[5-6]。基于嚴(yán)格理論模型的數(shù)值解法如矩量法(MOM)及基于矩量法的快速解法(如多層快速多極子算法(MLFMA))[7-8]從電磁場積分方程出發(fā)，可以精確求解三維復(fù)雜外形目標(biāo)的電磁散射。隨著高性能計(jì)算技術(shù)和低可探測飛行器的發(fā)展，基于精確建模的積分方程數(shù)值解法逐漸成為飛行器隱身設(shè)計(jì)中重要的電磁分析手段。

飛行器隱身性能與其外形密切相關(guān)，設(shè)計(jì)中常需處理隱身指標(biāo)與氣動(dòng)指標(biāo)之間的矛盾[9]。現(xiàn)有的氣動(dòng)隱身一體化設(shè)計(jì)多采用粒子群算法、遺傳算法、神經(jīng)網(wǎng)絡(luò)算法等智能搜索算法[1, 6, 9-10]。智能搜索算法具有收斂到全局最優(yōu)的能力，但優(yōu)化效率較低，優(yōu)化所需的雷達(dá)散射截面評(píng)估次數(shù)隨設(shè)計(jì)問題規(guī)模的增加迅速增加，與高精度電磁模擬方法結(jié)合時(shí)計(jì)算成本昂貴。基于梯度的優(yōu)化算法效率較高[11]，但經(jīng)典基于有限差分的RCS梯度計(jì)算代價(jià)大，限制了梯度算法在氣動(dòng)/隱身優(yōu)化中的應(yīng)用，目前對基于梯度的氣動(dòng)/隱身一體化優(yōu)化研究較少。基于伴隨思想的梯度求解方法可以通過一次原方程求解和一次伴隨方程求解得到目標(biāo)關(guān)于所有設(shè)計(jì)變量的導(dǎo)數(shù)，目前已在氣動(dòng)外形優(yōu)化[12]、氣動(dòng)/結(jié)構(gòu)耦合優(yōu)化[13]、聲爆優(yōu)化[14]等領(lǐng)域得到廣泛應(yīng)用。基于伴隨方法的優(yōu)化在隱身領(lǐng)域研究較少，Bondeson等[15]推導(dǎo)了二維積分形式的麥克斯韋連續(xù)伴隨方程，并對二維簡單外形(圓形)的RCS進(jìn)行了優(yōu)化；Wang和Anderson[16]推導(dǎo)了二維時(shí)域麥克斯韋方程的伴隨方程，通過給定翼型的目標(biāo)電流分布，對翼型的幾何進(jìn)行反設(shè)計(jì)；本文作者[17]在三維矩量法的基礎(chǔ)上推導(dǎo)了麥克斯韋方程的離散伴隨方程，驗(yàn)證了伴隨方法的精度，但仍面臨矩量法求解計(jì)算成本高、工程應(yīng)用困難的問題。

針對三維問題中高精度RCS評(píng)估梯度計(jì)算成本高的問題，本文引入麥克斯韋積分方程的伴隨方程，以三維矩量法為例詳細(xì)推導(dǎo)了麥克斯韋積分方程的離散伴隨方程和雷達(dá)散射截面的變分表達(dá)式。針對矩量法在三維復(fù)雜問題中內(nèi)存、計(jì)算量大的問題，采用多層快速多極子算法(MLFMA)進(jìn)行求解。選取雙椎體模型、導(dǎo)彈模型對求解器的計(jì)算精度、伴隨方法的可靠性進(jìn)行驗(yàn)證。計(jì)算結(jié)果表明本文采用的求解器有較高精度，基于矩量法、多層快速多極子算法伴隨梯度與差分梯度吻合良好，實(shí)現(xiàn)了通過兩次線性方程組求解獲得雷達(dá)散射截面關(guān)于所有設(shè)計(jì)變量的導(dǎo)數(shù)。證明了伴隨方法的可靠性和高效性，為基于梯度的高精度氣動(dòng)/隱身一體化優(yōu)化奠定基礎(chǔ)。

1 積分方程數(shù)值求解方法

本文采用矩量法和多層快速多極子算法求解麥克斯韋積分方程及其離散伴隨方程。矩量法是文獻(xiàn)[7]提出的一種用于嚴(yán)格計(jì)算電磁問題的數(shù)值方法。矩量法將積分形式的麥克斯韋方程離散后轉(zhuǎn)化為矩陣方程，通過求解線性方程組來得到目標(biāo)表面感應(yīng)電流，進(jìn)而計(jì)算散射場。快速多極子算法(FMM)[8]和多層快速多極子算法[18]是建立在矩量法和線性方程組迭代求解算法基礎(chǔ)上的快速算法。

1.1 基于RWG基函數(shù)的矩量法

RWG(Rao-Wilton-Glisson)基函數(shù)[19]是當(dāng)前使用較為廣泛的一種矩量法基函數(shù)，該基函數(shù)定義在具有公共邊的相鄰三角形上，可模擬任意形狀物體的表面電、磁流分布。對于RWG基函數(shù)矩量法，三角形剖分的網(wǎng)格邊長一般在[λ/12，λ/8]之間較為合適[20](λ為入射波長)。根據(jù)麥克斯韋方程和導(dǎo)體表面S上切向電場連續(xù)條件可得電場積分方程為

(1)

(2)

(3)

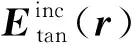
(4)

圖1 RWG基函數(shù)示意圖[21]Fig.1 Sketch of RWG basis function[21]

(5)

式中：In為第n個(gè)基函數(shù)的系數(shù)；N為三角形公共邊總數(shù)。采用RWG基函數(shù)作為檢驗(yàn)函數(shù)(伽略金法)，檢測電場積分方程可得

(6)

整理寫成矩陣形式：

ZN×NIN×1=VN×1

(7)

式中：Z為矩量法阻抗矩陣；I和V分別為電流系數(shù)向量和激勵(lì)向量。阻抗元素和激勵(lì)項(xiàng)的表達(dá)式為[7, 22]

(8)

(9)

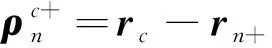
1.2 多層快速多極子算法

矩量法離散得到的阻抗矩陣是復(fù)數(shù)稠密矩陣，如果用直接法求解矩陣方程，則算法存儲(chǔ)量為O(e2)，計(jì)算量為O(e3)(相對于矩陣求逆運(yùn)算量級(jí))；如果用迭代法求解，存儲(chǔ)量為O(e2)，每步迭代的計(jì)算量為O(e2)(相對于矩陣矢量乘法運(yùn)算量級(jí))，其中e為未知量的個(gè)數(shù)。當(dāng)頻率增加時(shí)，未知量個(gè)數(shù)迅速增加，對內(nèi)存和計(jì)算速度提出了很高要求，限制了矩量法在高頻散射問題中的應(yīng)用。為提高矩量法求解問題的規(guī)模，在矩量法和線性方程組迭代求解算法的基礎(chǔ)上發(fā)展了快速多極子算法和多層快速多極子算法，將計(jì)算量和存儲(chǔ)量進(jìn)一步降低到O(e1.5)和O(elge)量級(jí)，使基于精確建模的積分方程數(shù)值解法求解電大尺寸目標(biāo)的電磁散射問題成為可能[23]。

快速多極子算法把基函數(shù)分為G組，將組之間的作用分為近相互作用和遠(yuǎn)相互作用，即將阻抗矩陣表示為

Z=Znear+Zfar

(10)

對于近相互作用，仍采用矩量法計(jì)算；對于遠(yuǎn)相互作用，則采用快速多極子算法。快速多極子算法利用加法定理和平面波展開定理將格林函數(shù)展開為多極子形式，進(jìn)而將矩陣與向量的乘積運(yùn)算轉(zhuǎn)化為聚合-轉(zhuǎn)移-配置3個(gè)過程。標(biāo)量格林函數(shù)G(r′,r)=e-jkR/R的多極子展開形式為

(11)

(12)

(13)

式中：

(14)

(15)

其中：ji和tj分別為電流J(r)的基函數(shù)和測試函數(shù);右端第1項(xiàng)表示鄰近組的貢獻(xiàn)；右端第2項(xiàng)為各遠(yuǎn)距離組的貢獻(xiàn)，通過式(14)、式(12)和式(15) 表示的聚合、轉(zhuǎn)移和配置3個(gè)步驟得到。

多層快速多極子算法是快速多極子算法的多層擴(kuò)展。多層快速多極子算法基于樹形結(jié)構(gòu)，通過在多個(gè)層級(jí)上分組，組間嵌套，逐層遞推來實(shí)現(xiàn)FMM[23]，進(jìn)一步降低了內(nèi)存需求，提高了矢量矩陣相乘的計(jì)算效率。由于FMM和MLFMA本質(zhì)上加速的是線性方程求解過程中矩陣和向量的乘積運(yùn)算，在計(jì)算過程中并不顯式存儲(chǔ)遠(yuǎn)相互作用矩陣。

2 基于伴隨方程的梯度計(jì)算

隱身優(yōu)化設(shè)計(jì)中常需要雷達(dá)散射截面關(guān)于設(shè)計(jì)變量的梯度信息。傳統(tǒng)的有限差分法計(jì)算梯度所需雷達(dá)散射截面的評(píng)估次數(shù)與設(shè)計(jì)變量個(gè)數(shù)成正比，當(dāng)設(shè)計(jì)變量較多時(shí)，有限差分法的計(jì)算代價(jià)較高，難以在實(shí)際問題中應(yīng)用。基于伴隨方程的梯度計(jì)算可以通過一次雷達(dá)散射截面求解、一次伴隨方程求解獲得雷達(dá)散射截面關(guān)于所有設(shè)計(jì)變量的梯度，有效提高梯度計(jì)算效率。本節(jié)在1.1節(jié)介紹的矩量法基礎(chǔ)上對離散伴隨方程和雷達(dá)散射截面的變分形式進(jìn)行推導(dǎo)[17]，并對伴隨方法所需的計(jì)算量和存儲(chǔ)量進(jìn)行簡要分析。

2.1 伴隨方程推導(dǎo)

典型的雷達(dá)散射截面優(yōu)化設(shè)計(jì)問題形式為

(16)

需要滿足的約束為

R(I(D),D)=V-ZI=0

(17)

式中：σ為雷達(dá)散射截面；I為感應(yīng)電流；D為設(shè)計(jì)變量。雷達(dá)散射截面是幾何外形和感應(yīng)電流的函數(shù)，在矩量法求解中阻抗矩陣、激勵(lì)和解得的感應(yīng)電流均只由幾何形狀決定，即

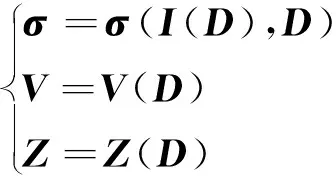
(18)

引入拉格朗日乘子Λ可以構(gòu)造目標(biāo)函數(shù)：

L=σ+ΛTR

(19)

對式(19)進(jìn)行求導(dǎo)，有

(20)

從式(20)可以看出，若找到合適的Λ使式(20) 右端第1項(xiàng)為0，可完全消除感應(yīng)電流對設(shè)計(jì)變量導(dǎo)數(shù)dI/dD的計(jì)算，大幅度降低計(jì)算量，即

(21)

注意到：

(22)

將式(22)代入式(21)即可得到伴隨方程：

(23)

伴隨方程的形式與正計(jì)算(RCS評(píng)估)的形式一致，可以直接采用正計(jì)算采用的數(shù)值方法(矩量法、多層快速多極子算法)求解。將式(23)代入式(20)，基于伴隨方法的目標(biāo)梯度可以寫為

(24)

(25)

2.2 雷達(dá)散射截面變分推導(dǎo)

伴隨方程式的右端項(xiàng)激勵(lì)?σ/?I為雷達(dá)散射截面關(guān)于感應(yīng)電流的導(dǎo)數(shù)，以1.1節(jié)中介紹的基于RWG基函數(shù)的三維矩量法為例對伴隨方程的激勵(lì)項(xiàng)進(jìn)行推導(dǎo)。

通過矩量法或多層快速多極子算法解得表面感應(yīng)電流分布后，則可以計(jì)算雷達(dá)散射截面標(biāo)量(m2)[24]，即

(26)

根據(jù)復(fù)數(shù)的運(yùn)算性質(zhì)將模的平方寫成自身與其共軛相乘的形式：

(27)

(28)

式中:上劃線表示共軛。由鏈?zhǔn)角髮?dǎo)法則：

(29)

復(fù)數(shù)求導(dǎo)需分別對復(fù)數(shù)的實(shí)部和虛部求導(dǎo)，即

(30)

則式(29)可以整理為

(31)

式(28)中：g離散后可以寫成感應(yīng)電流和的形式，當(dāng)采用1.1節(jié)介紹的RWG離散感應(yīng)電流時(shí)，具體表達(dá)式為

(32)

(33)

將式(33)代入式(31)，有

(34a)

(34b)

將式(34)進(jìn)一步代入式(30)即可得到伴隨方程右端項(xiàng)的表達(dá)式為

(35)

2.3 伴隨方法計(jì)算量和存儲(chǔ)量分析

基于伴隨方法的雷達(dá)散射截面導(dǎo)數(shù)求解主要由RCS正計(jì)算、伴隨方程求解、導(dǎo)數(shù)計(jì)算3部分構(gòu)成。

在RCS正計(jì)算中，矩量法需要一次阻抗矩陣填充和一次線性方程組求解；多層快速多極子算法需要多次計(jì)算ZI，計(jì)算次數(shù)與所需迭代次數(shù)成正比。當(dāng)采用迭代法求解時(shí)，2種算法的計(jì)算量和存儲(chǔ)量分別為O(e2)和O(elge)。在伴隨方程求解中，若正計(jì)算的阻抗矩陣為對稱陣，則矩量法可以直接使用正計(jì)算中的阻抗矩陣，不需要重新填充伴隨方程的阻抗矩陣，可通過一次線性方程組求解完成伴隨變量計(jì)算；多層快速多極子算法不顯式存儲(chǔ)阻抗矩陣，因此多層快速多極子算法在伴隨計(jì)算階段與正計(jì)算所需的計(jì)算量基本一致。

3 梯度驗(yàn)證

梯度驗(yàn)證采用基于電場積分方程的矩量法和快速多極子算法，線性方程組求解采用基于雙共軛梯度算法[25]的迭代法求解。雙共軛梯度算法較之普通的共軛梯度方法有較快收斂性，特別是在矩陣為對稱陣的情況下，可以有效降低方程組求解的計(jì)算量[23]，計(jì)算過程中取收斂閾值ε=10-5。本節(jié)采用計(jì)算電磁學(xué)經(jīng)典算例及實(shí)際工程中復(fù)雜外形對伴隨梯度的可靠性和精度進(jìn)行探討。

3.1 雙椎體模型

雙椎體模型長7.5 in(1 in=25.4 mm)，由2個(gè) 椎角分別為22.62°和46.4°的半椎拼接而成[26-27]，是EMCC(ElectroMagnetic Code Consortium)[27]提供用于校驗(yàn)計(jì)算電磁學(xué)代碼的標(biāo)準(zhǔn)算例之一。雙椎體模型兩端存在尖點(diǎn)，高頻方法難以準(zhǔn)確計(jì)算，需采用高精度數(shù)值求解方法。計(jì)算采用的雷達(dá)波頻率f=9 GHz，單站散射水平極化和垂直極化，網(wǎng)格平均尺寸約為λ/10，未知量總數(shù)e=11 094。采用矩量法、多層快速多極子算法計(jì)算，并用商用軟件和實(shí)驗(yàn)值(EXP)[26-27]校核計(jì)算結(jié)果。幾種算法的計(jì)算結(jié)果如圖2和圖3所示。本文采用的矩量法和多層快速多極子算法均與實(shí)驗(yàn)值及商用軟件FEKO矩量法的計(jì)算結(jié)果吻合良好，具有較高精度。

采用基于HMQ全局徑向基函數(shù)的域元法[28-29]對雙椎體模型進(jìn)行參數(shù)化，設(shè)計(jì)變量分布如圖4所示。采用基于矩量法、多層快速多極子算法的伴隨方法和基于矩量法的有限差分法求解各設(shè)計(jì)變量在Z方向的梯度，認(rèn)為基于矩量法的有限差分(FDD)結(jié)果為梯度的精確解。有限差分計(jì)算中擾動(dòng)量Δx=10-3m。設(shè)計(jì)變量A和B(見圖4)在各入射角度的導(dǎo)數(shù)計(jì)算結(jié)果如圖5和圖6所示。

圖2 雙椎體水平極化計(jì)算結(jié)果Fig.2 Numerical results of double-ogive horizontal polarization

基于伴隨的矩量法和快速多極子算法計(jì)算得到的梯度與有限差分得到的梯度在趨勢上吻合較好。其中，基于伴隨的矩量法與有限差分的計(jì)算結(jié)果基本一致，具有較高精度；多層快速多極子算法得到的梯度與有限差分在梯度較小的角域存在一定誤差，在梯度峰值附近吻合良好。入射角為0°時(shí)的感應(yīng)電流模值分布和伴隨電流模值分布如圖7所示。值得注意的是，在流場伴隨求解中，流場伴隨變量傳播方向與流場守恒變量相反[12]，而在電磁場求解中，電磁場伴隨變量分布與感應(yīng)電流分布較為一致。在求解過程中，共計(jì)算180個(gè)入射角度，其中矩量法計(jì)算使用20核并行計(jì)算，最大內(nèi)存占用1.85 G，總計(jì)算耗時(shí)42 min。多層快速多極子算法計(jì)算使用8核并行計(jì)算，最大內(nèi)存使用18.3 MB，計(jì)算用時(shí)3.7 min。

圖3 雙椎體垂直極化計(jì)算結(jié)果Fig.3 Numerical results of double-ogive vertical polarization

圖4 雙椎體設(shè)計(jì)變量分布Fig.4 Design variables distribution of double-ogive

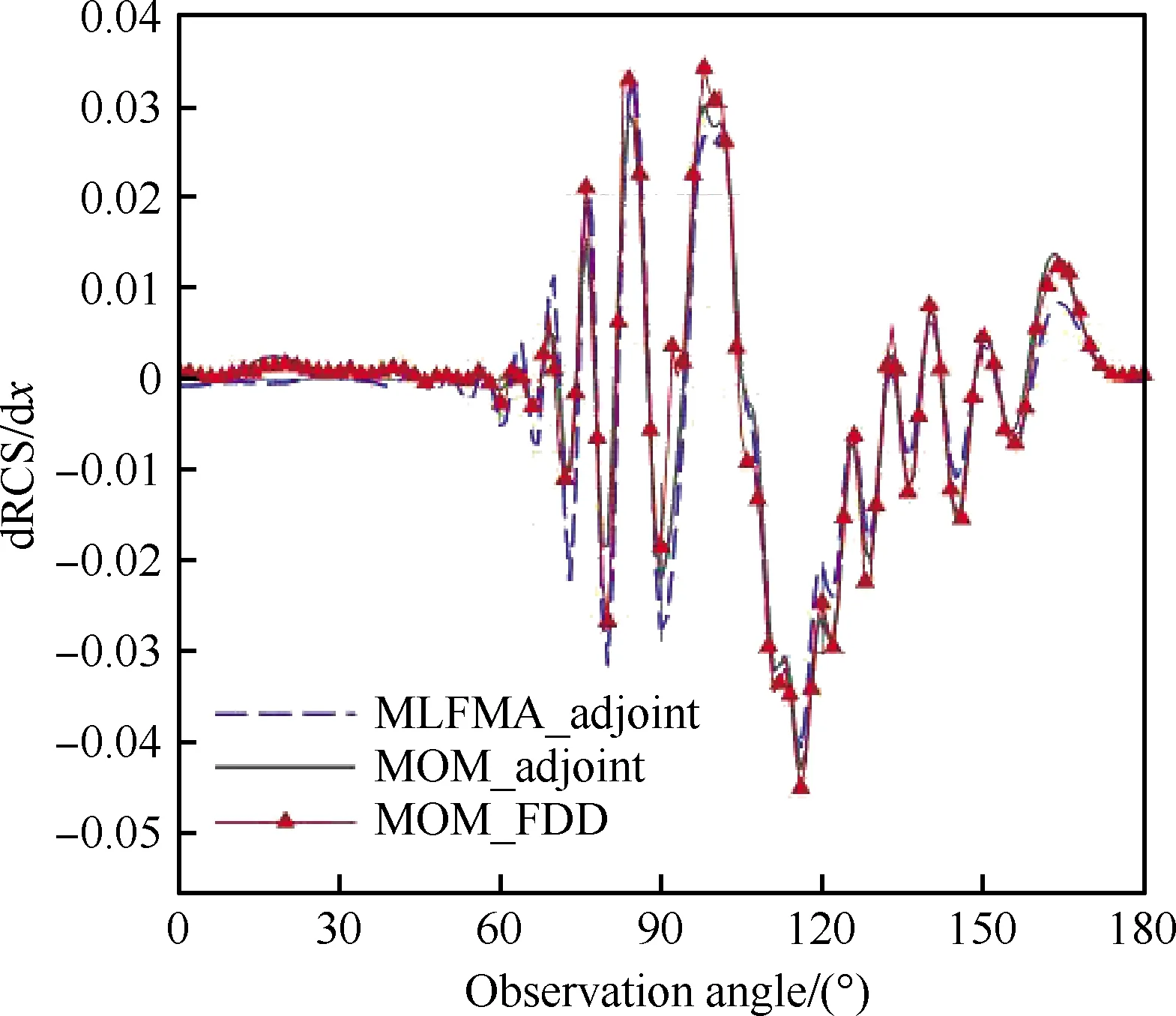
圖5 雙椎體設(shè)計(jì)變量A導(dǎo)數(shù)(水平極化)Fig.5 Gradients of double-ogive design variable A(horizontal polarization)

圖6 雙椎體設(shè)計(jì)變量B導(dǎo)數(shù)(水平極化)Fig.6 Gradients of double-ogive design variable B(horizontal polarization)

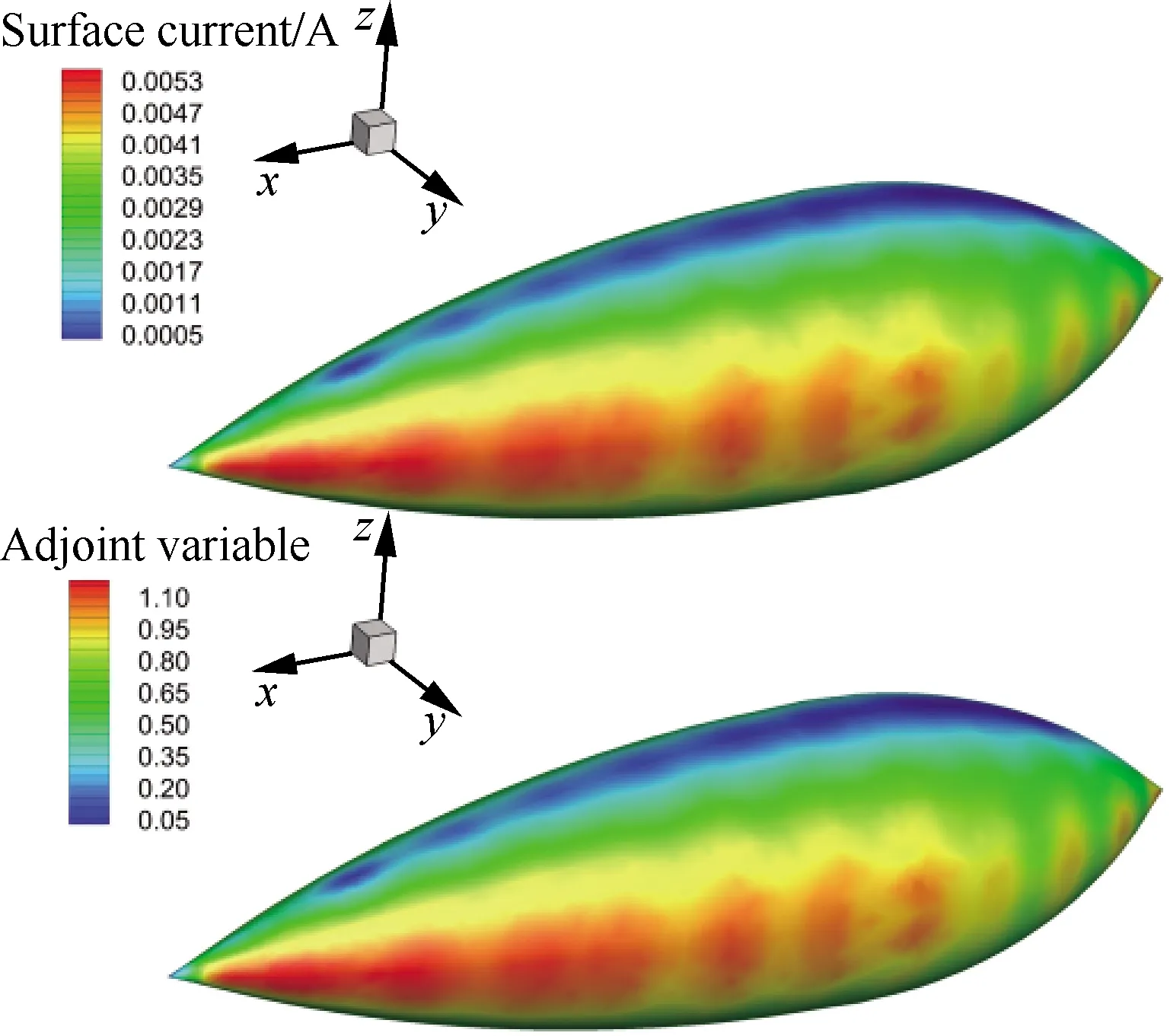
圖7 雙椎體感應(yīng)電流及伴隨變量云圖Fig.7 Contours of surface current and adjoint variable of double-ogive

3.2 導(dǎo)彈模型

導(dǎo)彈模型是宏觀上的電大尺寸和細(xì)節(jié)上的電小尺寸共存的復(fù)雜模型，具有較高的實(shí)際工程意義，對電磁散射計(jì)算和梯度計(jì)算提出了較高要求。計(jì)算采用的導(dǎo)彈模型全長4 m，彈體直徑0.28 m。計(jì)算采用雷達(dá)波段頻率f=1 GHz，單站散射水平極化。網(wǎng)格平均尺寸約為λ/10，未知量e=26 157。采用矩量法、多層快速多極子算法計(jì)算，并與商用軟件的矩量法進(jìn)行對比。幾種算法的計(jì)算結(jié)果對比如圖8所示，矩量法和多層快速多極子算法的計(jì)算結(jié)果一致性較好，與商用軟件的計(jì)算結(jié)果區(qū)別較小，具有較高的可信度。

采用基于HMQ全局徑向基函數(shù)的域元法對導(dǎo)彈模型進(jìn)行參數(shù)化，設(shè)計(jì)變量分布如圖9所示。采用基于矩量法、多層快速多極子算法的伴隨方法求解各設(shè)計(jì)變量在z方向的梯度并與基于矩量法的有限差分計(jì)算結(jié)果對比，計(jì)算中差分?jǐn)_動(dòng)量Δx=10-2m。其中設(shè)計(jì)變量C和D(如圖9所示)在各入射角度的梯度計(jì)算結(jié)果如圖10和圖11 所示。基于伴隨方法的矩量法和多層快速多極子算法得到的梯度與有限差分方法得到的梯度在趨勢上較為一致。其中，基于伴隨的矩量法與有限差分計(jì)算得到的梯度吻合較好，誤差較小；基于多層快速多極子算法的伴隨求解在梯度較小及梯度起伏較為劇烈的區(qū)域存在一定誤差。由圖10 和圖11可以看到，雷達(dá)散射截面的導(dǎo)數(shù)隨入射角度變化在大小和正負(fù)號(hào)上均存在明顯起伏。圖12為入射角為0°時(shí)表面感應(yīng)電流和伴隨變量的分布云圖。

圖8 導(dǎo)彈單站RCS結(jié)果(水平極化)Fig.8 RCS results of missile (horizontal polarization)

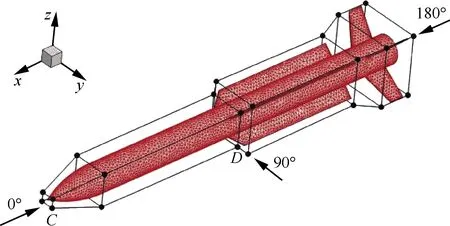
圖9 導(dǎo)彈模型表面網(wǎng)格Fig.9 Surface mesh of missile model

圖10 導(dǎo)彈設(shè)計(jì)變量C導(dǎo)數(shù)(水平極化)Fig.10 Gradients of missile design variable C(horizontal polarization)

圖11 導(dǎo)彈設(shè)計(jì)變量D導(dǎo)數(shù)(水平極化)Fig.11 Gradients of missile design variable D(horizontal polarization)

圖12 導(dǎo)彈感應(yīng)電流及伴隨變量云圖Fig.12 Contours of surface current and adjoint variable of missile

在導(dǎo)數(shù)求解過程中，矩量法計(jì)算中內(nèi)存使用10.4 G，計(jì)算使用20核并行計(jì)算，計(jì)算180個(gè)入射角度，總計(jì)算耗時(shí)608 min。多層快速多極子算法內(nèi)存使用25.4 MB，計(jì)算使用8核并行計(jì)算，計(jì)算用時(shí)57 min。

4 結(jié) 論

本文提出了一種基于麥克斯韋積分方程離散伴隨方程的RCS梯度計(jì)算方法，實(shí)現(xiàn)了RCS梯度的高效、高精度求解，為基于梯度的電大尺寸目標(biāo)高精度氣動(dòng)/隱身一體化優(yōu)化提供了基礎(chǔ)。

1) 麥克斯韋積分方程的離散伴隨方程形式與原積分方程一致，可直接采用原積分方程的數(shù)值解法如矩量法及多層快速多極子算法求解，程序?qū)崿F(xiàn)容易。

2) 伴隨方程的計(jì)算量與設(shè)計(jì)變量個(gè)數(shù)基本無關(guān)，可以實(shí)現(xiàn)通過2次線性方程組求解得到雷達(dá)散射截面關(guān)于所有設(shè)計(jì)變量的梯度信息。伴隨求解的計(jì)算量與原方程求解基本一致，存儲(chǔ)量在原方程求解的基礎(chǔ)上增加不明顯。

3) 基于伴隨方程的梯度求解方法具有較高精度，多層快速多極子算法求取的梯度在精度上雖然略低于矩量法的計(jì)算結(jié)果，但在計(jì)算時(shí)間和內(nèi)存需求上均明顯優(yōu)于矩量法，更適合于電大尺寸復(fù)雜問題的評(píng)估和優(yōu)化。