多液艙晃蕩與養(yǎng)殖工船時(shí)域耦合運(yùn)動(dòng)的數(shù)值模擬

肖凱隆，陳作鋼

1 上海交通大學(xué) 海洋工程國(guó)家重點(diǎn)實(shí)驗(yàn)室，上海 200240

2 高新船舶與深海開發(fā)裝備協(xié)同創(chuàng)新中心，上海 200240

3 上海交通大學(xué) 船舶海洋與建筑工程學(xué)院，上海 200240

0 引 言

我國(guó)是海水養(yǎng)殖發(fā)達(dá)國(guó)家之一，養(yǎng)殖面積和產(chǎn)量均居世界首位[1]。現(xiàn)階段，我國(guó)海水養(yǎng)殖方式還比較粗放，且內(nèi)陸和沿海的養(yǎng)殖空間受到擠壓，導(dǎo)致養(yǎng)殖密度過大、病害頻發(fā)、水產(chǎn)品品質(zhì)下降和環(huán)境惡化等問題日益突出[2]。因此，走向深遠(yuǎn)海、發(fā)展綠色養(yǎng)殖生產(chǎn)新方式已成必然趨勢(shì)。

深遠(yuǎn)海養(yǎng)殖工船作為深遠(yuǎn)海養(yǎng)殖的一個(gè)發(fā)展方向，集成了繁育、養(yǎng)殖、加工、冷凍冷藏等魚貨物供給的一條龍功能，可為階段性的分艙養(yǎng)殖、自動(dòng)化投喂、自動(dòng)排污、機(jī)械化起捕等提供先進(jìn)的養(yǎng)殖和生產(chǎn)手段。依托養(yǎng)殖工船進(jìn)行深遠(yuǎn)海養(yǎng)殖，可以實(shí)現(xiàn)高度集約化、生態(tài)化、規(guī)模化的健康養(yǎng)殖，同時(shí)將魚類養(yǎng)殖區(qū)域推向深遠(yuǎn)海，能拓展養(yǎng)殖空間，有效地推進(jìn)海洋漁業(yè)的轉(zhuǎn)型發(fā)展[3]。養(yǎng)殖工船通常系泊工作于水質(zhì)和風(fēng)浪條件合適的深遠(yuǎn)海海域，并汲取海水至養(yǎng)殖液艙。但液艙晃蕩產(chǎn)生的晃蕩力作用于船體，可能會(huì)加劇船體運(yùn)動(dòng)，使船舶安全性面臨更大的挑戰(zhàn)。因此，在設(shè)計(jì)階段對(duì)液艙晃蕩與船體運(yùn)動(dòng)的耦合作用進(jìn)行充分論證，是確保養(yǎng)殖工船安全性的關(guān)鍵。

目前，國(guó)內(nèi)外許多學(xué)者針對(duì)液艙晃蕩與船體時(shí)域耦合運(yùn)動(dòng)展開了研究。其中，液艙晃蕩的模擬方法主要有2 類：非線性勢(shì)流方法[4]和黏流方法[5]。船體運(yùn)動(dòng)預(yù)報(bào)主要基于勢(shì)流理論，采用脈沖響應(yīng)函數(shù)（IRF）法。船體運(yùn)動(dòng)預(yù)報(bào)和液艙晃蕩模擬分別采用勢(shì)流和黏流的方法，簡(jiǎn)稱為勢(shì)流—黏流耦合法；如果都采用勢(shì)流方法，則簡(jiǎn)稱為全勢(shì)流法。全勢(shì)流法假設(shè)艙內(nèi)液體無(wú)黏無(wú)旋，但當(dāng)晃蕩劇烈時(shí)，該假設(shè)就會(huì)出現(xiàn)局限性。勢(shì)流—黏流耦合法是基于CFD 理論模擬液艙晃蕩，以犧牲計(jì)算效率為代價(jià)來(lái)提高計(jì)算精度。勢(shì)流—黏流耦合法兼顧了勢(shì)流方法計(jì)算速度快以及CFD 方法相對(duì)準(zhǔn)確的優(yōu)點(diǎn)，基于此，李裕龍等[6]和操戈等[7]將計(jì)算結(jié)果與試驗(yàn)結(jié)果進(jìn)行對(duì)比，驗(yàn)證了該方法的可靠性。

本文將采用勢(shì)流—黏流耦合法計(jì)算液艙晃蕩與船體運(yùn)動(dòng)耦合的問題。首先，通過SESAM 軟件計(jì)算船體水動(dòng)力系數(shù)及波浪力，基于IRF 法計(jì)算時(shí)延函數(shù)，建立船體運(yùn)動(dòng)預(yù)報(bào)方程。接著，通過FLUENT 軟件數(shù)值模擬液艙晃蕩，采用流體體積（VOF）法捕捉自由面，并將液艙晃蕩力實(shí)時(shí)添加至船體運(yùn)動(dòng)方程，讓船體運(yùn)動(dòng)方程求解與液艙晃蕩模擬交替進(jìn)行，以隨著時(shí)間的步進(jìn)，重復(fù)解耦工作，然后在自由橫搖衰減試驗(yàn)的基礎(chǔ)上驗(yàn)證該方法的有效性。最后，計(jì)算得到船體運(yùn)動(dòng)幅值響應(yīng)算子（RAO），對(duì)比分析考慮液艙晃蕩力與不考慮液艙晃蕩力下的計(jì)算結(jié)果，探究液艙晃蕩力對(duì)船體運(yùn)動(dòng)的影響。同時(shí)，還將研究壁面剪切力對(duì)數(shù)值模擬液艙晃蕩準(zhǔn)確度的影響，并針對(duì)多液艙模型，探索一種二維計(jì)算方法，以極大地減小計(jì)算規(guī)模。

1 載液船舶在波浪上的運(yùn)動(dòng)預(yù)報(bào)理論

1.1 速度勢(shì)疊加理論

勢(shì)流理論假設(shè)流體無(wú)黏無(wú)旋，并引入速度勢(shì)φ描述流場(chǎng)。φ滿足

式中， ?為拉普拉斯算子。

根據(jù)疊加原理，可以把速度勢(shì)分解為入射勢(shì)φI、繞射勢(shì)φD、輻射勢(shì)φR，如果只保留一階項(xiàng)，則得到

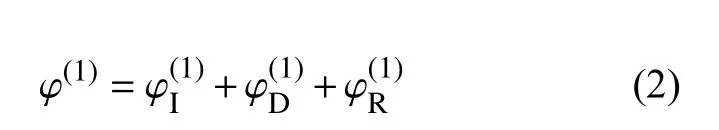
各項(xiàng)速度勢(shì)沿船體表面積分可得到流體對(duì)船體的各項(xiàng)作用力。其中，入射力FI是假設(shè)船體不存在時(shí)入射波在船體本該存在的位置產(chǎn)生的力；繞射力FD是假設(shè)船體固定時(shí)入射波繞射過船體所產(chǎn)生的力；輻射力FR是假設(shè)水面靜止時(shí)船體運(yùn)動(dòng)所產(chǎn)生的力。因此，一階波浪力為

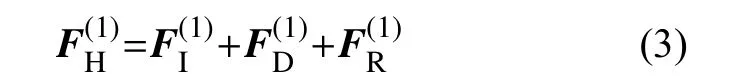
1.2 船舶頻域運(yùn)動(dòng)方程

根據(jù)牛頓第二定理，剛性船體的運(yùn)動(dòng)方程為

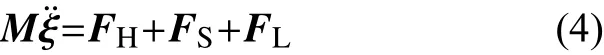
式中：M為船體質(zhì)量矩陣； ξ¨為船體加速度；FS=?Kξ ，為船體回復(fù)力，其中K為回復(fù)系數(shù)矩陣， ξ為船體位移；FL為船體受到的其他外力，如液艙晃蕩力。

根據(jù)輻射力的相關(guān)理論，F(xiàn)R為

將式（3）和式（5）代入式（4），得到船體頻域運(yùn)動(dòng)響應(yīng)方程

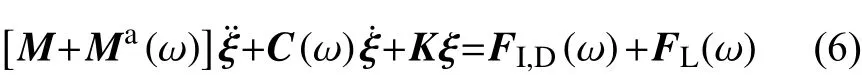
式中： ω為波浪頻率；FI,D為Froude-Kriloff 力，為入射力與繞射力之和，表示船體在規(guī)則波中受到的波浪激勵(lì)力[8]。

流體黏性對(duì)船體運(yùn)動(dòng)，特別是橫搖運(yùn)動(dòng)影響很大，通常是對(duì)橫搖阻尼添加線性項(xiàng)來(lái)彌補(bǔ)勢(shì)流理論中黏性的缺失。

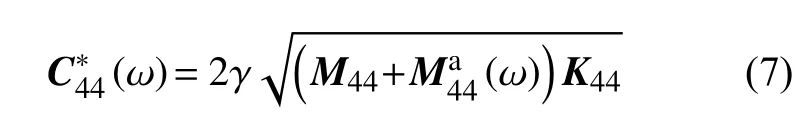
式中， γ為臨界阻尼系數(shù)，其取值與船型有關(guān)，無(wú)舭龍骨時(shí)，其取值范圍為2%～4%[9]。

1.3 基于脈沖響應(yīng)函數(shù)法的載液船舶時(shí)域運(yùn)動(dòng)方程

將船體在波浪中的響應(yīng)看作線性系統(tǒng)，通過IRF 法可以將一階波浪輻射力表示成時(shí)延函數(shù)R(t)與速度時(shí)歷 ξ˙(t)的卷積形式[10]。

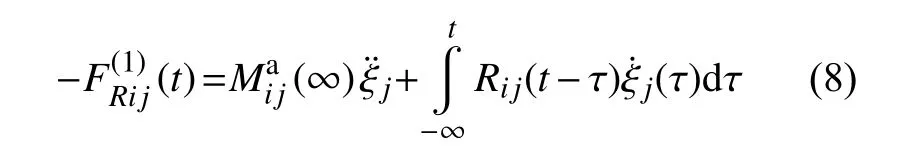
式中：R為時(shí)延函數(shù)；t為時(shí)間；τ為時(shí)間積分量；ij為矩陣角標(biāo)。無(wú)窮大遭遇頻率的附加質(zhì)量和Rij(t)為

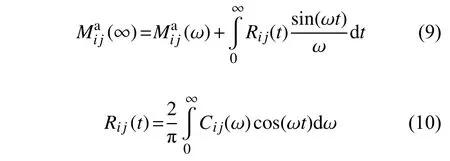
將式（6）中的波浪激勵(lì)力FI,D和液艙晃蕩力FL用時(shí)歷的形式表示，同時(shí)將波浪輻射力用式（8）表示，得到液艙晃蕩與船體運(yùn)動(dòng)時(shí)域耦合方程為

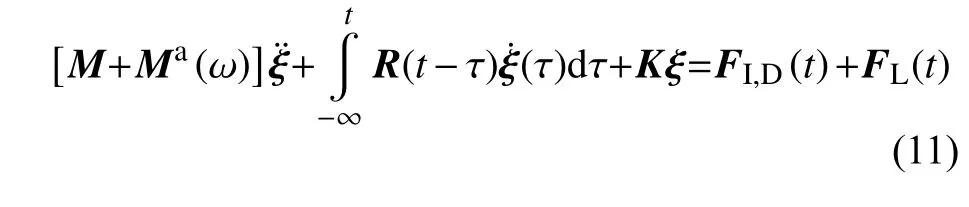
2 時(shí)域耦合方程的數(shù)值計(jì)算方法

本文將基于水動(dòng)力學(xué)軟件SESAM 計(jì)算船體質(zhì)量、附加質(zhì)量、阻尼系數(shù)和波浪載荷等水動(dòng)力系數(shù)，基于CFD 軟件FLUENT 數(shù)值模擬液艙晃蕩，并在用戶自定義函數(shù)（UDF）中實(shí)時(shí)將晃蕩力添加至船體運(yùn)動(dòng)方程。具體運(yùn)算步驟為：

1） 采用SESAM 軟件計(jì)算船體水動(dòng)力系數(shù)，直接輸入或等待UDF 讀取；

2） 給液艙設(shè)置微小的初始速度作為第1 個(gè)時(shí)間步的邊界條件；

3） 采用軟件FLUENT 計(jì)算當(dāng)前時(shí)間步的液艙晃蕩力，并添加至船體運(yùn)動(dòng)方程；

4） 求解船體運(yùn)動(dòng)方程，給出下一時(shí)間步的船體運(yùn)動(dòng)速度，并將其作為液艙新時(shí)間步下的運(yùn)動(dòng)邊界條件；

5） 步驟3）和步驟4）交替進(jìn)行，隨著時(shí)間的步進(jìn)，重復(fù)解耦工作，直至計(jì)算結(jié)束。

本次參觀交流活動(dòng)，為雙方在戰(zhàn)略層面上達(dá)成了共識(shí)，作為國(guó)內(nèi)鐘表行業(yè)唯一的研究所與目前國(guó)際上頂級(jí)的機(jī)心制造商來(lái)說，不斷的加強(qiáng)交流與合作，不僅是達(dá)成雙方共贏的商業(yè)目的，更多是企業(yè)發(fā)展理念的契合，乃至為鐘表行業(yè)發(fā)展盡一份力量。

UDF 的編制及計(jì)算過程需考慮以下細(xì)節(jié)：

1） UDF 在軟件FLUENT 中運(yùn)行時(shí)，新時(shí)間步下自定義物理量會(huì)被重新定義，而求解船體運(yùn)動(dòng)方程需要參考?xì)v史物理量，因此要將有關(guān)物理量定義成靜態(tài)變量，以避免在新時(shí)間步被清空。

2） 為避免每一時(shí)間步都要重新計(jì)算時(shí)延函數(shù)，可編寫外部程序預(yù)先計(jì)算，并在UDF 運(yùn)行的初始時(shí)刻讀取。

3） 船體水動(dòng)力是基于船體運(yùn)動(dòng)重心位置確定的，轉(zhuǎn)換液艙晃蕩力至船體運(yùn)動(dòng)方程或?qū)⒋w運(yùn)動(dòng)響應(yīng)轉(zhuǎn)換至液艙晃蕩邊界條件時(shí)，需要根據(jù)實(shí)際情況確定。

3 不規(guī)則多液艙簡(jiǎn)諧晃蕩的數(shù)值模擬

3.1 養(yǎng)殖工船物理模型

養(yǎng)殖工船垂線間長(zhǎng)241 m、型寬48 m、型深18.5 m，經(jīng)快速性多目標(biāo)數(shù)值優(yōu)化[11]，得到型線圖如圖1 所示。在主甲板下設(shè)置了關(guān)于船舯對(duì)稱的6 對(duì)養(yǎng)殖水艙，其中艏、艉2 對(duì)為不規(guī)則液艙，船舯4 對(duì)為尺寸一致的矩形規(guī)則液艙，各液艙高度均為16.1 m，載液率為75%。圖2 所示為液艙簡(jiǎn)化俯視圖，圖中僅繪制了1 對(duì)規(guī)則液艙來(lái)代替4 對(duì)規(guī)則液艙。

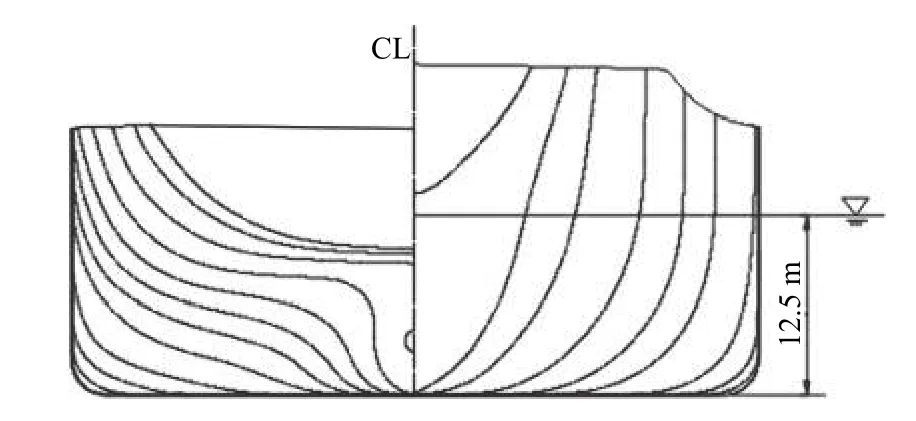
圖 1 養(yǎng)殖工船型線圖Fig. 1 Lines plan of the aquaculture ship

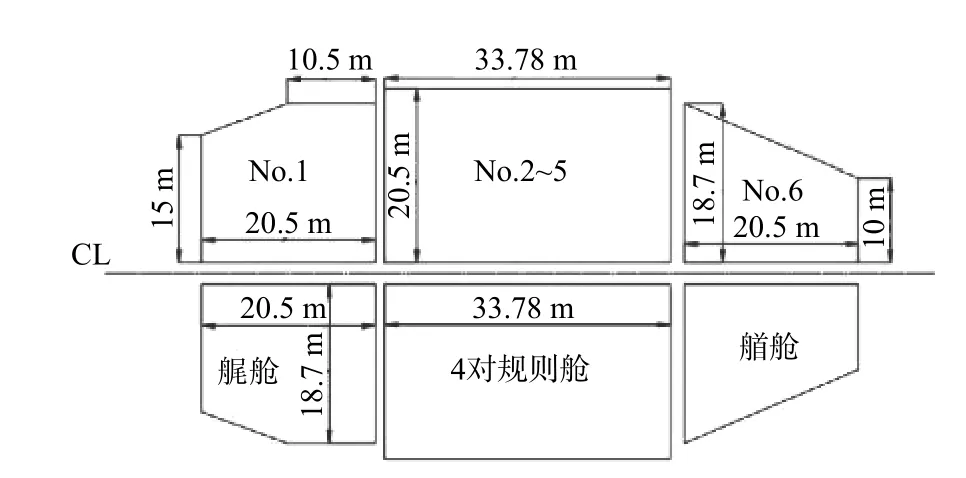
圖 2 液艙俯視圖Fig. 2 Top view of the multi-tank

3.2 壁面剪切力對(duì)液艙晃蕩數(shù)值模擬的影響

正確處理壁面黏性效應(yīng)，是CFD 數(shù)值模擬的關(guān)鍵。壁面函數(shù)法是常用的壁面處理方法，其本質(zhì)是在黏性子層及過渡層使用稱為壁面函數(shù)的半經(jīng)驗(yàn)公式計(jì)算壁面與充分發(fā)展湍流區(qū)域之間的黏性影響區(qū)域。壁面函數(shù)的使用依賴于壁單位（Wall unit）y+的正確選取，y+表示第一層網(wǎng)格與壁面間的無(wú)量綱距離，其計(jì)算公式可參考文獻(xiàn)[13]。當(dāng)壁面函數(shù)選取增強(qiáng)壁面處理（Enheanced wall treatment）時(shí)，要求y+保持在5 以下。

壁面函數(shù)法對(duì)y+的要求導(dǎo)致壁面附近的網(wǎng)格量劇增、計(jì)算時(shí)間變長(zhǎng)。若壁面黏性效應(yīng)對(duì)液艙晃蕩影響極小，不妨將壁面設(shè)置為滑移壁面，此時(shí)壁面附近沒有強(qiáng)剪切，離壁第1 層網(wǎng)格的高度也不再受壁面函數(shù)的約束。本文設(shè)置了3 組案例（Case1, Case2, Case3)來(lái)對(duì)比驗(yàn)證壁面剪切力對(duì)液艙晃蕩數(shù)值模擬的影響。

3 組案例均采用30 m×16 m 的二維矩形液艙，載液率均為50%，液艙繞其中的點(diǎn)作頻率為0.085cos0.6trad/s 的橫搖運(yùn)動(dòng)。其壁面函數(shù)的選擇與網(wǎng)格劃分情況如表1 所示。

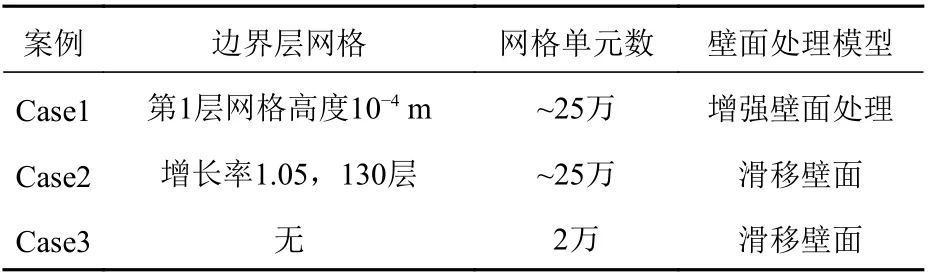
表 1 計(jì)算案例的網(wǎng)格及壁面處理模型Table 1 Mesh and wall treatment model for calculating cases

Case1 與Case2 均采用壁面加密結(jié)構(gòu)網(wǎng)格，如圖3 所示。要滿足y+小于5，Case1 采用增強(qiáng)壁面處理的壁面函數(shù)法；Case2 選擇滑移壁面作為邊界條件，忽略壁面剪切力；Case3 采用均勻的結(jié)構(gòu)網(wǎng)格，同樣忽略壁面剪切力。

圖 3 Case1，Case2 采用的精細(xì)化網(wǎng)格及其邊界層Fig. 3 Refined mesh and boundary layer used in Case1 and Case2

圖4 為3 組案例相對(duì)回轉(zhuǎn)中心的晃蕩力矩系數(shù)d的計(jì)算結(jié)果。由圖可見，3 條曲線基本重合，但由于網(wǎng)格單元數(shù)減少了90%以上，導(dǎo)致Case3的計(jì)算時(shí)間減少了約80%。因此，可以認(rèn)為壁面剪切力對(duì)液艙晃蕩的數(shù)值模擬影響不大，可以選擇滑移壁面作為壁面條件，同時(shí)采用均勻的結(jié)構(gòu)網(wǎng)格，降低網(wǎng)格數(shù)量，提高計(jì)算效率。

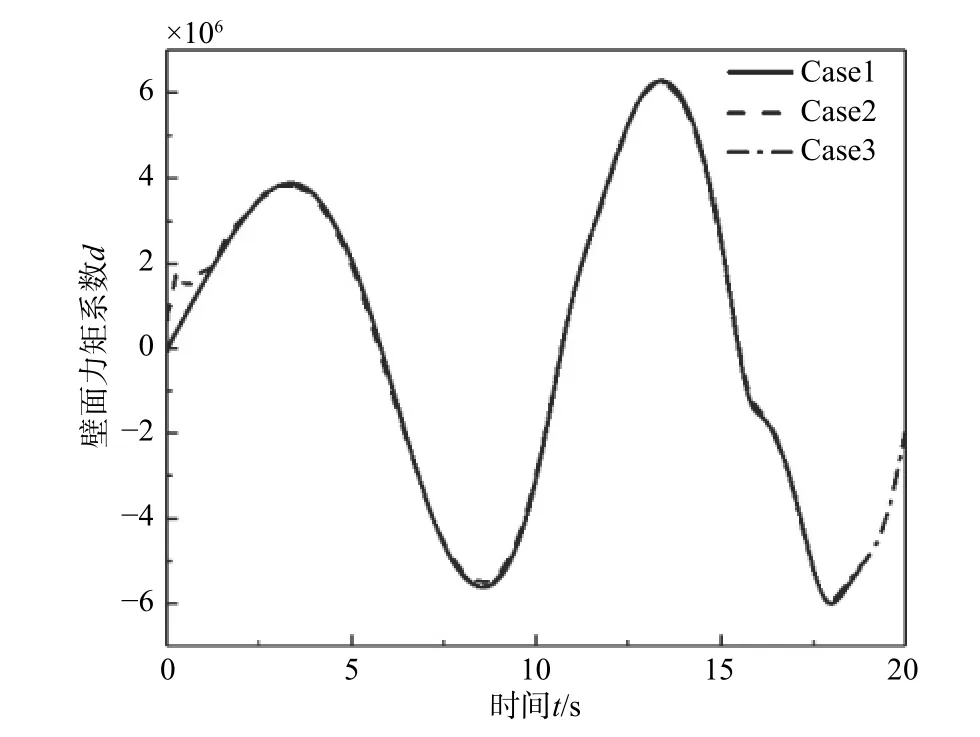
圖 4 相對(duì)回轉(zhuǎn)中心的壁面力矩系數(shù)Fig. 4 Moment coefficients relative to the center of rotation

4 數(shù)值求解方法的有效性驗(yàn)證

為了驗(yàn)證本文數(shù)值方法的有效性，本節(jié)對(duì)養(yǎng)殖工船模型在載液率為62.5%時(shí)的靜水橫搖自由衰減試驗(yàn)進(jìn)行了數(shù)值模擬。

4.1 橫搖自由衰減運(yùn)動(dòng)的模型試驗(yàn)

試驗(yàn)在上海交通大學(xué)循環(huán)水槽中進(jìn)行，該水槽試驗(yàn)段長(zhǎng)8 m，寬3 m。根據(jù)水槽尺寸，試驗(yàn)?zāi)Ｐ涂s尺比選為1∶100。試驗(yàn)開始前，利用慣量架測(cè)量船模轉(zhuǎn)動(dòng)慣量及重心位置。安裝、調(diào)整壓載鐵，使吃水位于設(shè)計(jì)水線處，并記錄壓載鐵的數(shù)量和位置。

試驗(yàn)時(shí)，人工施加恒力于一側(cè)船舷，使船體產(chǎn)生穩(wěn)定的初始橫傾角，當(dāng)船體內(nèi)、外水靜止后釋放船體，船體開始做自由橫搖衰減運(yùn)動(dòng)，同時(shí)用陀螺儀記錄橫搖角時(shí)歷。圖5 所示為載液及壓載鐵安裝示意圖。

圖 5 載液及壓載鐵安裝示意圖Fig. 5 Water in tanks and ballast iron installation

4.2 數(shù)值模擬結(jié)果與試驗(yàn)結(jié)果對(duì)比

在已知船模、壓載鐵、液艙水體的重心位置和質(zhì)量的情況下，根據(jù)初穩(wěn)性理論可以求出橫搖回復(fù)力系數(shù)K。假設(shè)船體繞著重心所在軸線做自由橫搖，可以求出轉(zhuǎn)動(dòng)慣量。采用SESAM 軟件計(jì)算橫搖阻尼系數(shù)及附加轉(zhuǎn)動(dòng)慣量。

FLUENT 數(shù)值模擬液艙晃蕩中，經(jīng)網(wǎng)格無(wú)關(guān)性驗(yàn)證，設(shè)置液艙模型網(wǎng)格尺寸為6 mm，時(shí)間步長(zhǎng)為0.005 s，迭代步數(shù)為60。

圖6 所示為試驗(yàn)與數(shù)值模擬得到的橫搖角時(shí)歷對(duì)比圖，圖中同時(shí)還繪制了不考慮液艙晃蕩的模擬結(jié)果。可以發(fā)現(xiàn)，考慮液艙晃蕩的數(shù)值模擬結(jié)果與試驗(yàn)結(jié)果吻合良好，證明本文數(shù)值方法對(duì)液艙晃蕩與船體運(yùn)動(dòng)耦合方程的求解有效。

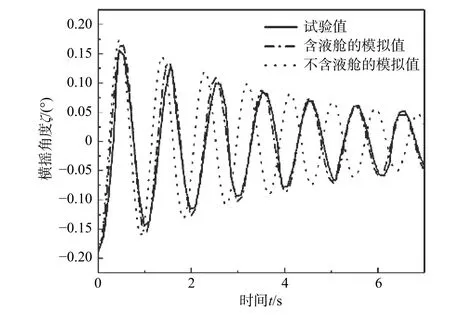
圖 6 試驗(yàn)與數(shù)值模擬的橫搖角時(shí)歷對(duì)比Fig. 6 Comparison of roll angle between test and numerical simulation

5 實(shí)船計(jì)算結(jié)果與分析

5.1 船體水動(dòng)力系數(shù)、時(shí)延函數(shù)及CFD 參數(shù)設(shè)置

橫搖臨界阻尼系數(shù)λ取3%時(shí)，SESAM 軟件計(jì)算得到的橫搖阻尼系數(shù)C44如圖7(a)所示；由式（10）計(jì)算出的時(shí)延函數(shù)R44如圖7(b)所示；波高2 m時(shí)的一階波浪橫搖力矩F44如圖7(c)所示。

液艙晃蕩的數(shù)值模擬中，經(jīng)網(wǎng)格無(wú)關(guān)性驗(yàn)證，網(wǎng)格模型尺寸取為0.6 m，時(shí)間步長(zhǎng)為0.005 s，每一時(shí)間步的迭代步數(shù)為20。初始時(shí)刻液艙自由面示意圖如圖8 所示。

5.2 RAO 時(shí)域計(jì)算結(jié)果

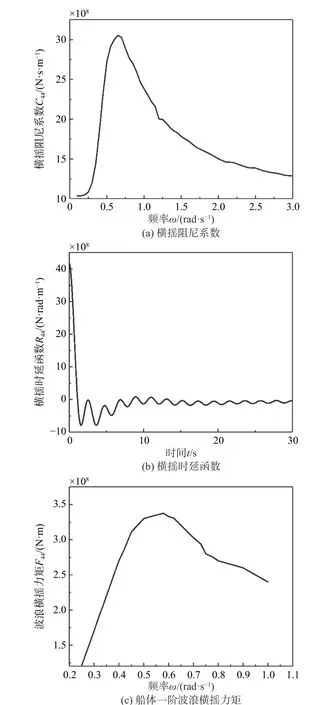
圖 7 橫搖阻尼系數(shù)、時(shí)延函數(shù)以及一階波浪橫搖力矩Fig. 7 Damping coefficient and retardation functions of rolling and First-order wave rolling moment

圖 8 初始時(shí)刻液艙自由面示意圖Fig. 8 The free surface of tanks in the initial moment

圖9 所示為橫向規(guī)則波激勵(lì)下，考慮液艙晃蕩力和不考慮液艙晃蕩力情況下計(jì)算得到的橫搖RAO4及升沉RAO3。如圖9(a)所示，當(dāng)波浪頻率較低時(shí)，液艙晃蕩力會(huì)加大船舶橫搖運(yùn)動(dòng)幅值；而在波浪頻率較高時(shí)，橫搖幅值有所降低，液艙起到了減搖水艙的作用。同時(shí)，考慮液艙晃蕩力時(shí)，RAO4的峰值較不考慮液艙晃蕩力時(shí)的情況增大了43%，且峰值對(duì)應(yīng)的波浪頻率有所降低。如圖9(b)所示，當(dāng)波浪頻率較低時(shí)，液艙晃蕩力會(huì)加大船舶升沉運(yùn)動(dòng)幅值；而在波浪頻率較高時(shí)，船舶運(yùn)動(dòng)幅值有所降低。考慮液艙晃蕩力后，RAO3在頻率更低的位置達(dá)到了峰值，且峰值略大于不考慮液艙晃蕩力的情況。

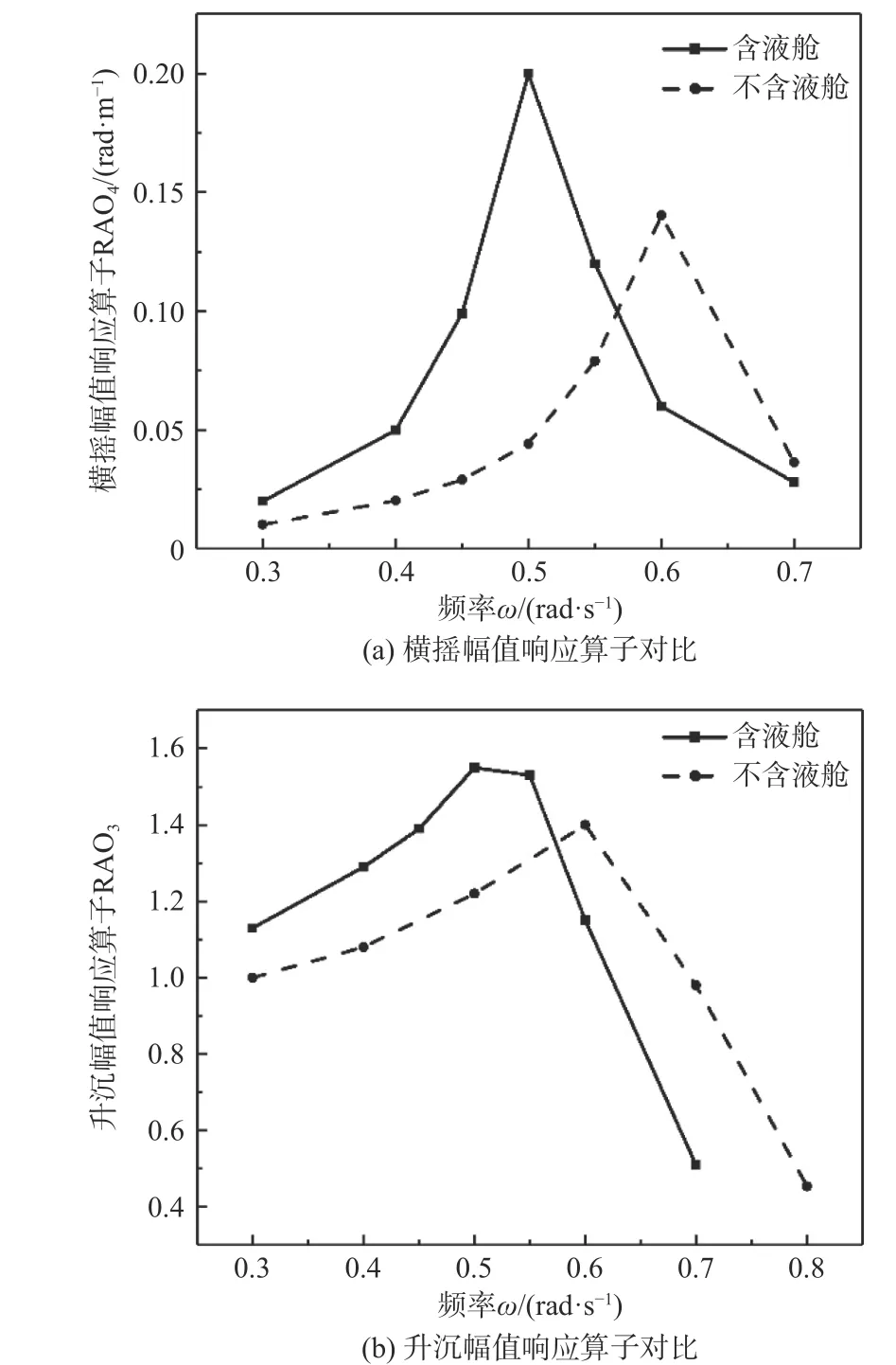
圖 9 橫搖、升沉幅值響應(yīng)算子對(duì)比Fig. 9 Comparison of roll and heave response amplitude operator

5.3 液艙晃蕩力對(duì)養(yǎng)殖工船運(yùn)動(dòng)的影響

如圖9(a)所示，在波浪頻率ω=0.4，0.6 rad/s的激勵(lì)情況下，液艙晃蕩力會(huì)分別增大、減小船體橫搖運(yùn)動(dòng)幅度。本節(jié)將對(duì)比分析橫搖運(yùn)動(dòng)時(shí)歷及有關(guān)力矩，以說明液艙晃蕩力對(duì)船體運(yùn)動(dòng)的影響機(jī)制。

圖10(a)所示為在波浪頻率ω=0.4 rad/s 的橫向規(guī)則波激勵(lì)下，考慮液艙晃蕩力和不考慮液艙晃蕩力的船體橫搖運(yùn)動(dòng)時(shí)歷ξ4(t)對(duì)比，圖10(b)所示為晃蕩橫搖力矩與波浪橫搖力矩時(shí)歷F4(t)的對(duì)比。從中可以看出，運(yùn)動(dòng)穩(wěn)定后，晃蕩橫搖力矩與波浪橫搖力矩的相位十分接近，此時(shí)，液艙晃蕩力將增大船體橫搖運(yùn)動(dòng)幅度。

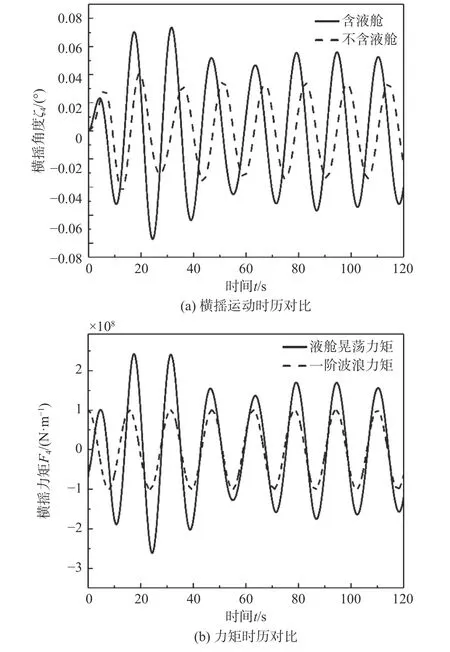
圖 10 船體運(yùn)動(dòng)及相關(guān)力矩的對(duì)比（ω=0.4 rad/s）Fig. 10 Comparison of hull motion and moment（ω=0.4 rad/s）

圖11(a)所示為在波浪頻率ω=0.6 rad/s 的橫向規(guī)則波激勵(lì)下，考慮液艙晃蕩力和不考慮液艙晃蕩力的船體橫搖運(yùn)動(dòng)時(shí)歷對(duì)比，圖11(b)所示為晃蕩橫搖力矩與波浪橫搖力矩的時(shí)歷對(duì)比。從中可以看出，運(yùn)動(dòng)穩(wěn)定后，晃蕩橫搖力矩與波浪橫搖力矩相位相差較大，此時(shí)，液艙晃蕩力將降低船體橫搖運(yùn)動(dòng)幅度。

6 多液艙晃蕩的二維簡(jiǎn)化計(jì)算

本文雖然用1 對(duì)規(guī)則液艙代替了4 對(duì)規(guī)則液艙，但受限于計(jì)算規(guī)模，仍有必要進(jìn)一步簡(jiǎn)化計(jì)算模型。圖12 所示為波浪頻率ω=0.5 rad/s 時(shí)，艏、艉液艙橫搖力矩與4 對(duì)規(guī)則液艙橫搖力矩的對(duì)比，從中可以看出，前者數(shù)值較小，因而對(duì)船體運(yùn)動(dòng)的影響有限。

圖13 所示為液艙總橫搖力矩與規(guī)則液艙橫搖力矩的比值k隨頻率ω的變化示意圖。如圖所示，k的變化范圍很小，可近似認(rèn)為總力矩與規(guī)則液艙力矩間的比值恒定。因此，可選取某一波浪頻率下的k作為所有頻率下的定值，并將k倍的規(guī)則液艙力矩近似看作總力矩，以避免計(jì)算艏、艉不規(guī)則艙。波浪頻率ω=0.5 rad/s 對(duì)應(yīng)的k值為1.131，選其為本文定值k。

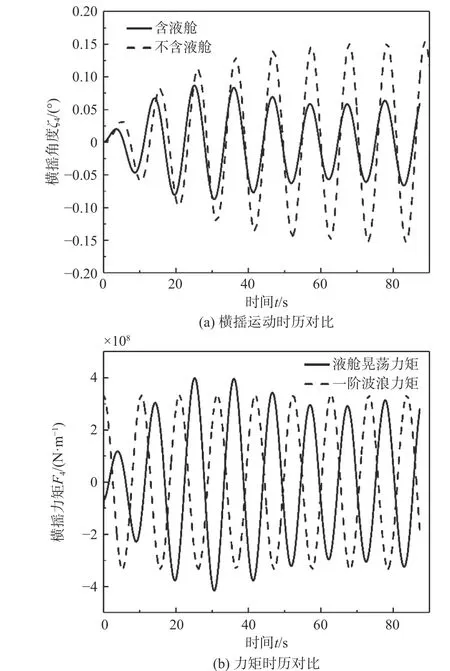
圖 11 船體運(yùn)動(dòng)及相關(guān)力矩對(duì)比 (ω=0.6 rad/s)Fig. 11 Comparison of hull motion and moment (ω=0.6 rad/s)

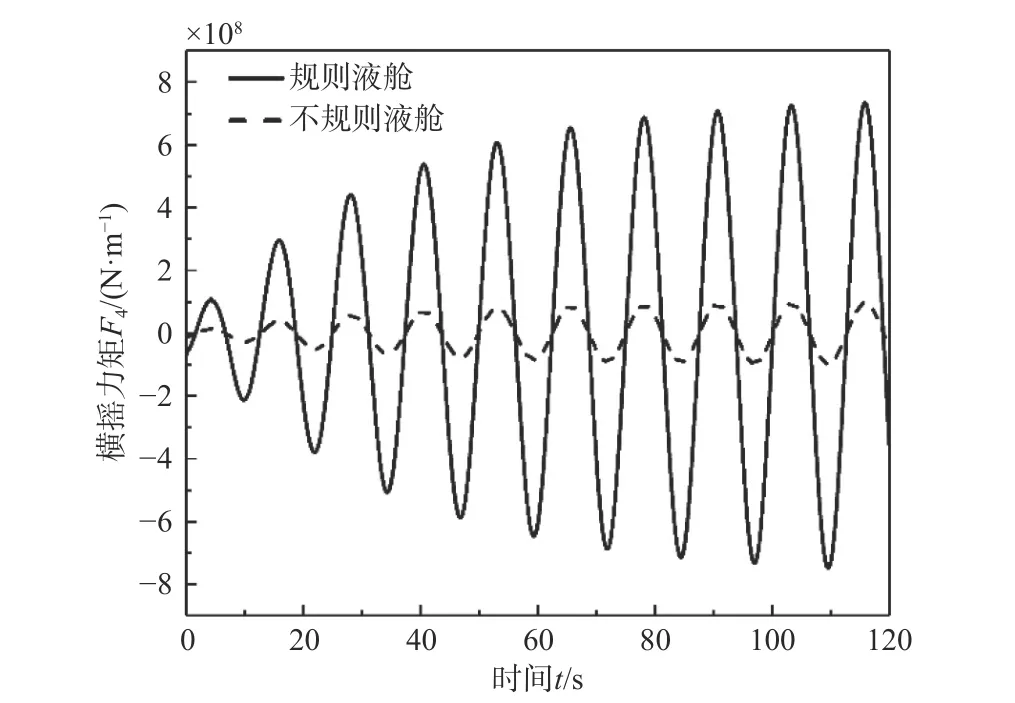
圖 12 規(guī)則艙與不規(guī)則艙橫搖力矩對(duì)比（ω=0.5 rad/s）Fig. 12 Comparison of rolling moment between regular tank and irregular tank (ω=0.5 rad/s)

矩形液艙長(zhǎng)、寬比大于1 時(shí)，三維液艙晃蕩與二維液艙晃蕩的數(shù)值模擬結(jié)果經(jīng)過長(zhǎng)度換算后吻合良好[14]。養(yǎng)殖工船規(guī)則液艙的長(zhǎng)寬比約為1.6，可數(shù)值模擬其二維橫截面液艙晃蕩，并將晃蕩力乘以液艙長(zhǎng)度代替三維液艙的晃蕩力，以進(jìn)一步簡(jiǎn)化模型。

通過引入?yún)?shù)k替代艏、艉不規(guī)則艙的晃蕩模擬以及采用二維模型代替三維液艙模型的策略，可將計(jì)算效率提升90%以上。

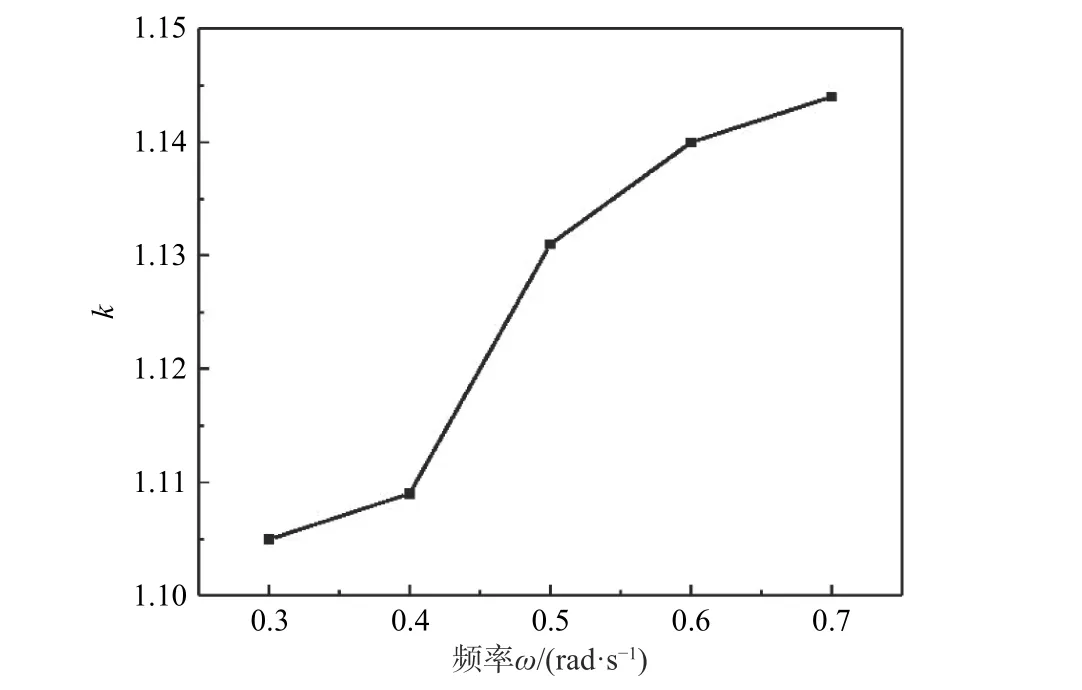
圖 13 k 隨頻率ω 的變化Fig. 13 Variation of k with respect to frequency ω

圖14 所示為在波浪頻率ω=0.3，0.7 rad/s 的激勵(lì)下，通過二維方法計(jì)算的與包含不規(guī)則液艙的三維方法計(jì)算得到的船體橫搖運(yùn)動(dòng)時(shí)歷對(duì)比。雖然k取波浪頻率ω=0.5 rad/s 對(duì)應(yīng)的值，但在波浪頻率ω=0.3，0.7 rad/s 情況下的橫搖運(yùn)動(dòng)模擬中，二維計(jì)算結(jié)果與三維計(jì)算結(jié)果吻合良好，表明用單一波浪頻率下的k近似代替其他頻率下的k是可行的。同時(shí)也表明，用二維液艙模型代替三維規(guī)則液艙模型來(lái)計(jì)算液艙晃蕩是可行的。

圖 14 二維和三維液艙晃蕩船體橫搖運(yùn)動(dòng)時(shí)歷對(duì)比Fig. 14 Comparison of ship rolling between 2D and 3D mutli-tank

如圖9（a）所示，在波浪頻率ω=0.5 rad/s 時(shí)RAO4達(dá)到峰值，該頻率下，波幅為1 m 的橫向波浪可使船體橫傾角最大達(dá)到11.5°。圖15 所示為在該波浪激勵(lì)下，船體運(yùn)動(dòng)穩(wěn)定后左傾、右傾達(dá)到最大位置以及在中間位置處（從左到右）的液艙晃蕩云圖。從中可以看出，由于周期較大，橫搖角度較小，即使在RAO4峰值對(duì)應(yīng)的波浪條件下，艙內(nèi)水體的晃蕩依然比較平穩(wěn)，自由液面也未發(fā)生明顯形變。

圖 15 不同時(shí)刻的液艙晃蕩云圖（ω=0.5 rad/s）Fig. 15 The contours of tank sloshing at different times

7 結(jié) 論

本文求解了多液艙養(yǎng)殖工船在橫向規(guī)則波激勵(lì)下的時(shí)域響應(yīng)，得出如下主要結(jié)論：

1） 考慮壁面剪切力與否對(duì)液艙晃蕩的數(shù)值模擬影響不大，壁面條件可選擇滑移壁面，同時(shí)采用均勻結(jié)構(gòu)網(wǎng)格代替邊界加密網(wǎng)格，提高計(jì)算效率。

2） 載液量較大時(shí)，液艙晃蕩力會(huì)對(duì)船體運(yùn)動(dòng)產(chǎn)生明顯影響。液艙晃蕩力與波浪力相位接近時(shí)，將增大船體運(yùn)動(dòng)幅度；反之，將減小。對(duì)于養(yǎng)殖工船，液艙晃蕩力對(duì)船體橫搖運(yùn)動(dòng)影響較大。不考慮液艙晃蕩力時(shí)，橫搖RAO 在波浪頻率ω=0.6 rad/s 達(dá)到峰值，為0.14 rad/m；考慮液艙晃蕩力時(shí)，在波浪頻率ω=0.5 rad/s 達(dá)到最大，為0.20 rad/m，增大了43%。

3） 養(yǎng)殖工船艏、艉不規(guī)則艙液量較少，對(duì)船體運(yùn)動(dòng)影響有限，可將某一波浪頻率下，液艙總晃蕩力與規(guī)則液艙晃蕩力的比值視作該比值在所有波浪頻率下的值，從而避免計(jì)算艏、艉不規(guī)則液艙的晃蕩。對(duì)于規(guī)則艙，可用其二維橫截面模型代替三維液艙模型，進(jìn)一步簡(jiǎn)化計(jì)算。