跨海橋梁高樁承臺波浪沖擊荷載概率模型

魏 凱，周 聰，徐 博

(西南交通大學土木工程學院橋梁工程系，四川，成都 610031)

跨海橋梁作為“21 世紀海上絲綢之路”的關鍵節點，起到互聯互通的作用，具有重要的戰略意義[1]。不同于陸地，復雜多變的海洋環境給橋梁基礎設計帶來了新的挑戰[2－3]。高樁承臺作為常用的跨海橋梁基礎形式之一，廣泛應用于東海大橋、杭州灣跨海大橋、港珠澳大橋等重大工程。極端波浪條件下，上部承臺結構將承受強烈的波浪沖擊荷載作用[4]。2016 年臺風“莫蘭蒂”期間，正在施工中的平潭海峽公鐵兩用跨海大橋高樁承臺就受到了極端波浪沖擊荷載作用。高樁承臺因為上部質量大，側向剛度小，在波浪沖擊作用下，水平向的動力響應會明顯大于按照靜力方法算得的結構響應[5]。結構安全將因此受到嚴重威脅[6]。然而，目前關于極端波浪沖擊荷載時變規律的研究并不完善，難以對跨海橋梁高樁承臺的動力分析提供有效指導。

蘭雅梅[7]研究發現，波浪作用于高樁承臺底部時的壓強分布與波浪周期、波陡及承臺凈空有關。任冰等[8]采用SOLA-VOF 方法，通過數值模擬，得到海洋平臺波浪沖擊荷載的時程曲線，主要針對波浪力的豎直分量，對水平分量的研究并不充分。

設計工作中，為簡化計算，許多規范都采用沖擊系數法計算波浪沖擊荷載的水平分量，如美國石油學會采用的(API 規范)[9]、挪威船級社采用的(DNV 規范)[10]、美國國家公路與運輸學會標準采用的(AASHTO 規范)[11]。郭安薪等[12－13]基于水槽實驗，提出了計算極端波浪作用下橋面板水平力、豎向力和彎矩最大值的解析公式，但上述方法均無法反映波浪沖擊荷載隨時間的變化歷程。

為反映波浪沖擊荷載隨時間變化的關系，波浪沖擊作用被修正為包含時間變量的形式[14]。Wienke等[15]把沖擊過程分為兩階段，并給出了各階段的波浪力時程和時間區間的理論計算公式。van Raaij等[14]通過擬合數值計算結果，提出了三段式時程模型描述海洋平臺受到的波浪沖擊荷載，并給出了各階段持續時間的經驗值。這些研究雖然描述了波浪荷載的時程特性，但并未考慮波浪沖擊荷載顯著的隨機性，以均值、最大值等作為荷載代表值，無法準確分析結構可靠度。

Hattori 等[16]發現，波浪沖擊防波堤或直墻類結構時，沖擊荷載峰值和沖擊上升段持續時間存在指數關系。但不同模型的經驗系數存在較大差異。上述研究表明，采用概率方法描述隨機性明顯的波浪沖擊荷載更為合適。Copula 是一類將多個隨機變量的聯合分布和他們各自的邊緣分布連接起來的函數[17]。Copula 函數能描述變量的相關性，且不受各變量的邊緣分布形式限制[18]。Serinaldi 等[19]就采用Copula 函數描述了波浪沖擊沿海橋梁橋面板時，沖擊荷載峰值和沖擊上升時間的關系。

因此，本文以跨海大橋高樁承臺為研究對象，通過試驗和理論分析手段，開展如下工作：1) 進行極端波浪沖擊高樁承臺尺縮模型的水槽試驗；2) 基于試驗結果，建立了波浪沖擊荷載時程模型，探明波浪沖擊荷載水平分量的時變規律；3) 以Copula理論為基礎，建立了沖擊荷載峰值和沖擊上升段持續時間的聯合概率模型。

1 高樁承臺波浪沖擊水槽試驗

1.1 水槽試驗設計

本文以平潭海峽公鐵兩用跨海大橋所用的高樁承臺為研究對象。該承臺為36 m×24 m×13.5 m 的長方體，依據1∶90 的縮尺比加工試驗模型。在西南交通大學深水大跨橋梁實驗室的長60 m、寬2 m、高1.8 m 的中型波流水槽中開展波浪沖擊高樁承臺的模型試驗。試驗模型布置于距造波機27.95 m 處，模型安裝如圖1 所示。水深取90 cm，模型凈空s(承臺底面與靜水面之間的距離)分別取0 cm、2 cm、4 cm。

圖1 模型安裝 Fig.1 Model installation

試驗中入射波采用Strokes 五階波。為造出波峰尖而陡的非線性極端波浪，在試驗中選取給定波高下的周期最短波陡最大的波浪條件。為此，首先對試驗水槽進行極端規則波浪條件率定，選取波高H為9 cm、12 cm、15 cm、18 cm、21 cm。通過不斷縮短波浪周期，直到造出的波浪達到破碎極限，繼續縮短則會造成波浪破碎，此周期即為該波高條件下的極端波浪周期率，得出的不同極端波浪條件下的波高、周期關系如式(1)。將選定的波高H代入式(1)，求得相應波高條件下的最短周期T為0.91 s、1.04 s、1.15 s、1.25 s、1.35 s。

根據不同凈空、波浪條件組合確定15 組試驗工況，如表1 所示。

選用采樣頻率為1000 Hz 的六分量測力天平采集模型受到的沖擊力水平分量。為獲得模型受波浪作用時的周圍液面變化情況，將采樣頻率為100 Hz的波高儀分別布置在承臺后方(WG4)及兩側 (WG2、WG3) 10 cm 處。在空水槽測試中，將波高儀WG1安裝于WG4 前方2 m 處以監測波浪條件，當試驗模型安裝就位后，將WG1 重新安裝于承臺前方40 cm 處。模型及儀器布置如圖2 所示。

本試驗波浪條件符合Stokes 五階波浪理論，根據該理論計算波面歷時曲線并與空水槽試驗結果進行對比，如圖3 所示。由圖知，對于試驗采用的五種波浪條件，試驗和理論的吻合較好，且波浪傳播的穩定性高，波峰與波谷未發生明顯的抬升與下降情況，試驗水槽可以滿足本文波浪試驗要求。

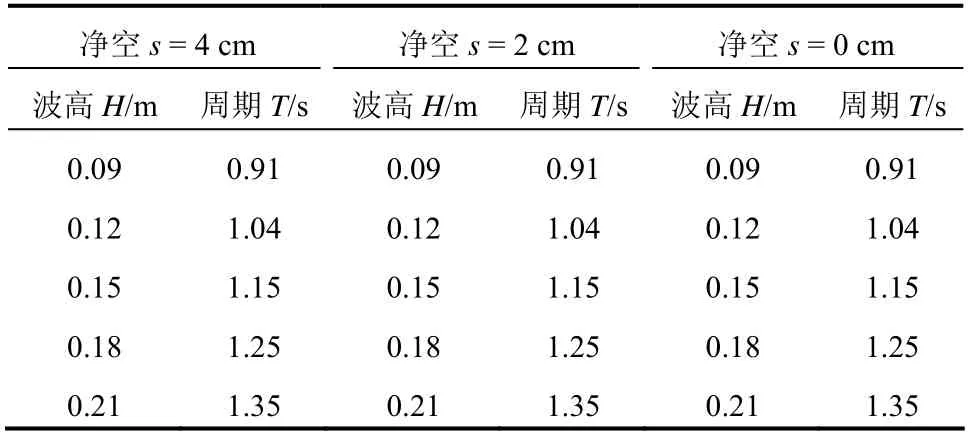
表1 試驗工況 Table 1 Experimental conditions

圖2 模型及儀器布置 Fig.2 Model and instrument layout

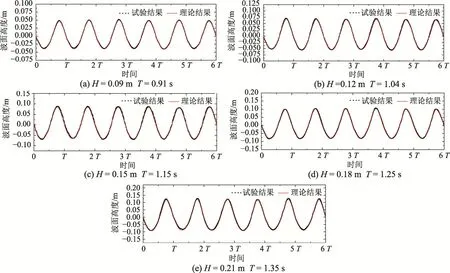
圖3 空水槽造波驗證 Fig.3 Wave making verification of empty flume

1.2 數據處理

對各工況下試驗穩定段的波浪沖擊荷載時程進行頻域分析。依據分析結果，分別以結構自振的上限、下限頻率15.48 Hz 和12.44 Hz 為截斷頻率，采用3 階Butterworth 低通濾波器進行濾波，消除結構自振干擾。由圖4 可知，當截斷頻率為結構自振的下限頻率時，噪聲基本被過濾。因此，采用下限頻率的濾波結果。在波浪即將離開承臺時，水體作用于承臺后部，產生負向波浪力。由于波面下降，承臺快速與水體分離。因而，負向波浪力不僅數值較小，而且持續時間較短。同時，在負向波浪力中未見沖擊成分，故不納入考慮范圍。截取荷載時程中的正向部分，提取正向荷載時程中的沖擊荷載峰值、沖擊上升段持續時間及沖擊持續時間用于分析。

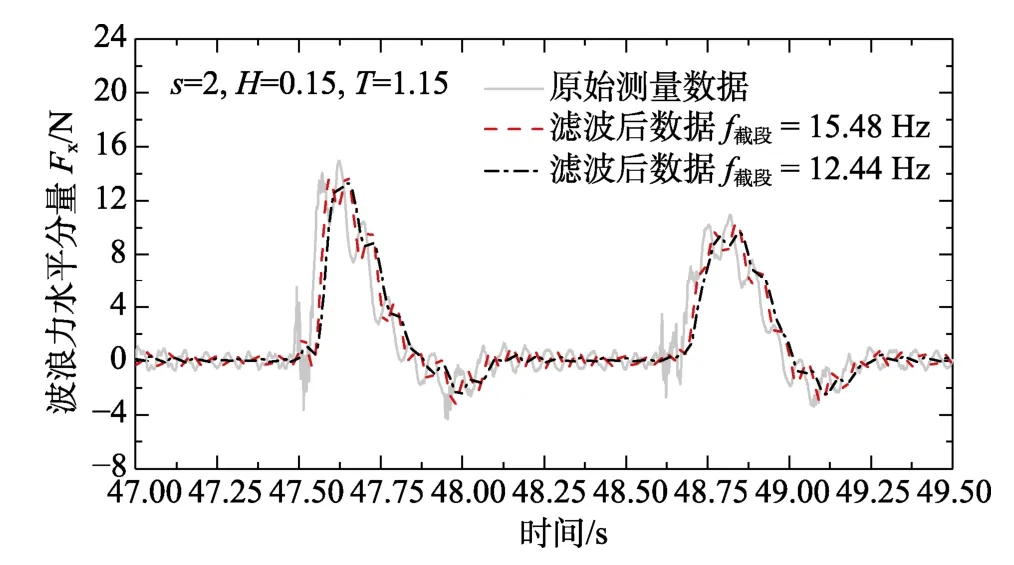
圖4 原始數據與濾波結果對比 Fig.4 Raw data and filtered data was compared

2 波浪沖擊荷載時程模型

基于沖擊荷載峰值和沖擊上升段持續時間對截取的正向波浪沖擊荷載時程進行歸一化處理。同一工況，不同來波的沖擊荷載時程形狀如圖5 所示。

為反映圖5 所示的沖擊荷載時變規律，將波浪沖擊荷載時程表示為沖擊荷載峰值Fxmax與時變函數f(tr,td,t)的乘積，基本形式如下：

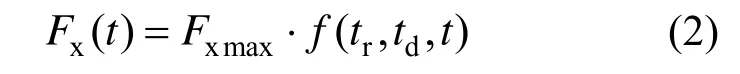
式中：Fx(t)為隨時間變化的沖擊荷載；tr為沖擊上升段持續時間；td為沖擊持續時間。

如圖5 所示，同一工況下，不同來波歸一化后的沖擊荷載時程呈現明顯的不對稱性。進一步觀察可發現波浪沖擊上升段的時程可采用三角函數的組合形式來近似，而下降段可采用冪函數來近似。因而，沖擊荷載的時變特性可表述為式(3)的分段函數形式。只需確定沖擊荷載峰值、沖擊上升段持續時間及沖擊持續時間即可確定沖擊過程。由圖3 可知，式(3)擬合效果較好。

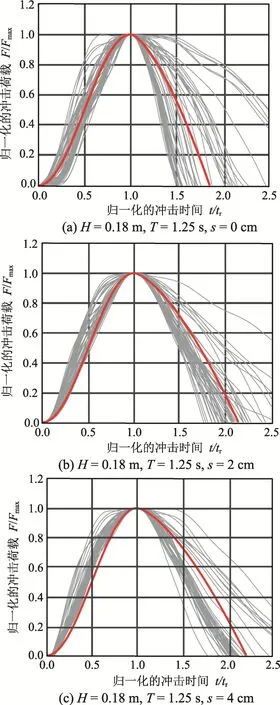
圖5 歸一化的波浪沖擊荷載時程 Fig.5 Normalized time history curve of wave impact

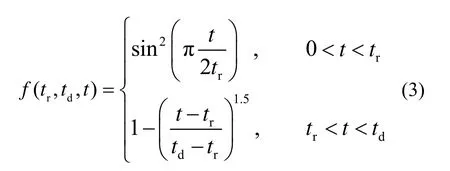
為確定沖擊過程，對沖擊荷載峰值、沖擊上升段持續時間及沖擊持續時間進一步研究。在已有研究基礎上，通過分析實驗中的參數變量，發現沖擊荷載峰值主要與波峰高度ηmax(波峰距靜水面的高度)、承臺底面凈空s以及承臺迎水面寬度a相關。采用量綱分析法，確定沖擊荷載峰值計算公式：

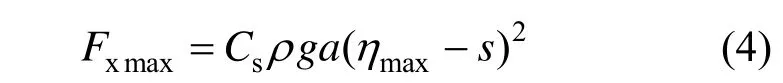
式中：Cs為無量綱系數；ρ ga(ηmax-s)2為初始峰值。通過最小二乘法得到Cs的最佳估計值為0.374。

對于tr和td，分析它們的散點圖，發現二者存在較強正相關性，線性相關系數ρ= 0.9047，因而由沖擊上升段持續時間tr就可確定沖擊持續時間td。通過回歸分析可得式(5)：

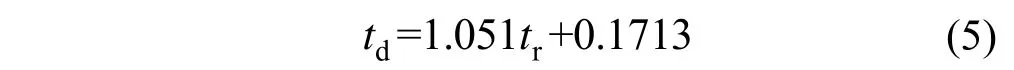
將式(5)代入式(3)可得簡化的時變函數f：

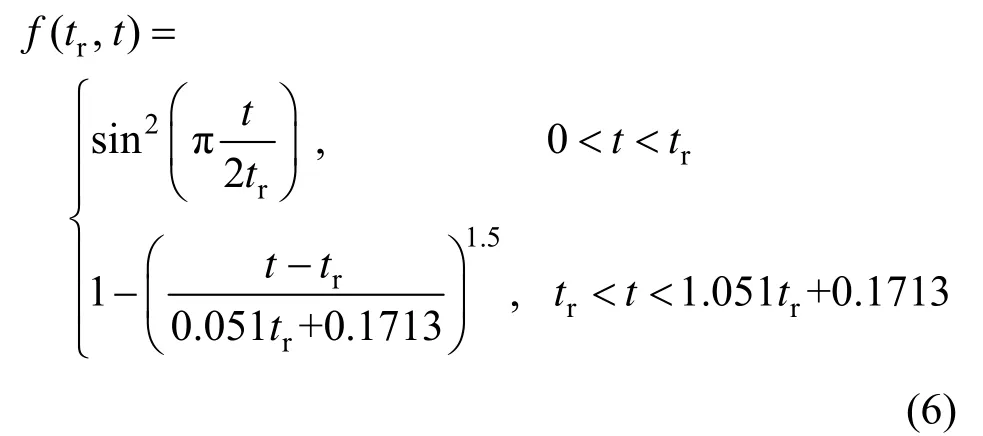
由圖6 可知，沖擊荷載峰值和沖擊上升段持續時間均具有離散性，式(4)和式(5)無法對此進行有效描述。若取Cs=1.6，雖能充分保證結構的可靠性， 卻無法兼顧經濟性。

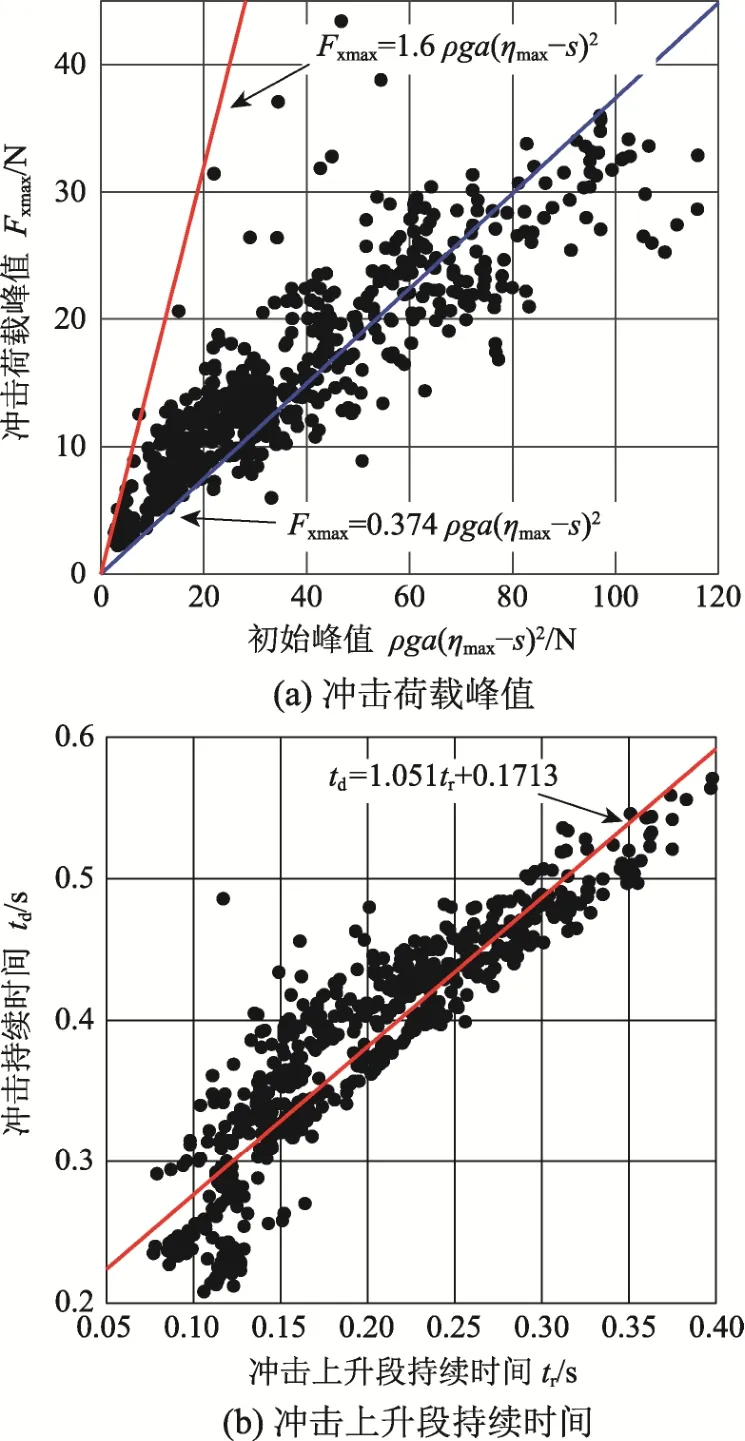
圖6 沖擊荷載峰值和沖擊上升段持續時間的線性擬合 Fig.6 Linear fitting of impact maxima and rise time

同時，已有研究表明沖擊荷載峰值Fxmax與沖擊上升段持續時間tr并非完全獨立，存在一定的負相關性[20－21]。因而，采用Copula 函數建立沖擊荷載峰值Fxmax和沖擊上升段持續時間tr的聯合概率分布，以描述它們之間的聯系。

3 基于Copula 的波浪沖擊荷載概率模型

根據二元分布Sklar[22]定理，基于二維Copula理論的聯合概率模型如下：

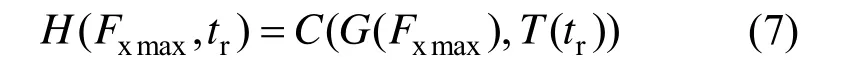
式中，G(Fxmax)、T(tr)為H(Fxmax,tr)的邊緣分布。若G(Fxmax)、T(tr)連續，則C唯一確定。

3.1 邊緣分布

建立聯合概率模型需要確定沖擊荷載峰值和沖擊上升段持續時間的邊緣分布形式。先將它們進行無量綱處理。沖擊荷載峰值的無量綱量可由式(4)直接寫出：

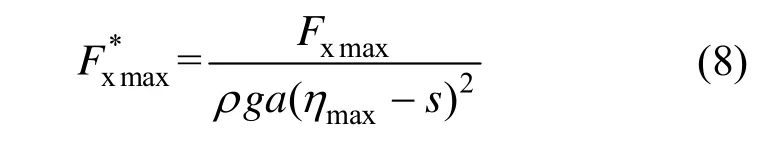
據試驗可知，沖擊上升段持續時間與波高，波浪周期、承臺底部凈空有關。試驗中，周期與波高采用了指定關系。在其他條件不變的情況下，沖擊上升段持續時間僅與周期和凈空有關，其無量綱量為：

式中：T為波浪周期；s為凈空；d為水深。

分別采用Gamma 分布、廣義極值(GEV)分布、Generalized Pareto(GP)分布、Inverse Gaussian 分布、Lognormal 分布、Rayleigh 分布、t-Location-Scale分布等對無量綱沖擊荷載峰值和無量綱沖擊上升段持續時間進行擬合，運用極大似然法進行參數估計，結果如表2 和圖7 所示。

如圖7 所示，不同概率模型對無量綱沖擊荷載峰值和無量綱沖擊上升段持續時間的概率分布擬合效果參差不齊。采用K-S檢驗遴選擬合度最高的概率分布模型。由表3 可知，無量綱沖擊荷載峰值滿足GEV 分布，其函數表達如下：

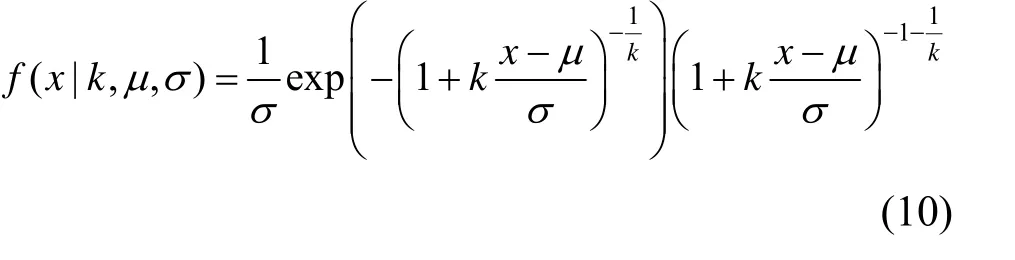
表2 概率密度函數參數估計結果 Table 2 Probability density function parameter estimation result

式中，k= 0.123，μ= 0.425，σ= 0.138。

由表4 可知，無量綱沖擊上升段持續時間最符合Beta 分布，其函數表達如下：

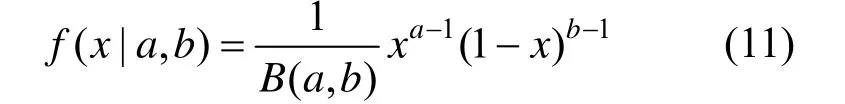
式中，a= 20.625，b= 67.031。

3.2 Copula 函數的確定

選取Gaussian Copula、t Copula、Frank Copula、Farile-Gumbel-Morgenstern (FGM) Copula、 AMH Copula等10種應用廣泛的阿基米德Copula函數族，采用Bayes 方法進行參數估計[23]，具體方法如下：

假 設Θ表 示 參 數θ= (θ1,θ2,…,θk)的 可 能 取值，則相應的先驗概率分布為pi=P(Θ=θi)。令ε為觀測結果，利用觀測結果修正參數θ的先驗假定分布，依據條件概率公式可得：

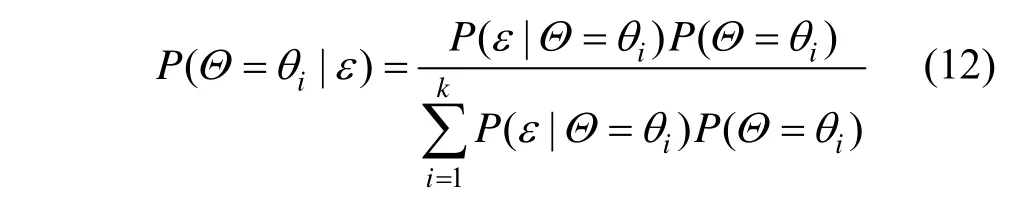
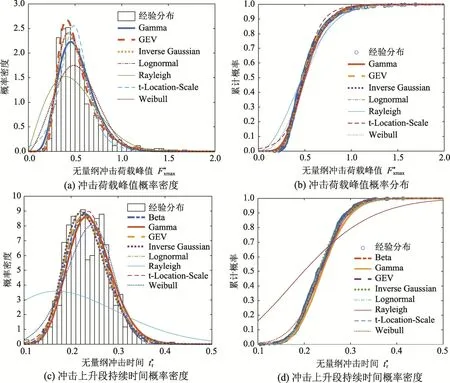
圖7 不同聯合概率模型擬合結果對比 Fig.7 Fitting results of different joint probability model was compared

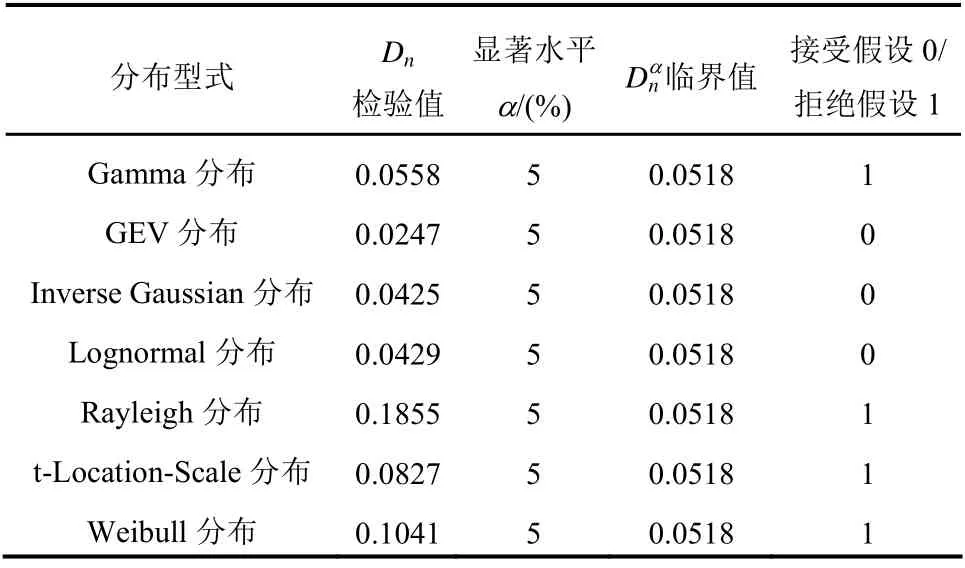
表3 無量綱沖擊荷載峰值各理論概率分布K-S 檢驗結果 Table 3 K-S test results of different theoretical probability distributions of non-dimensional wave impact maxima

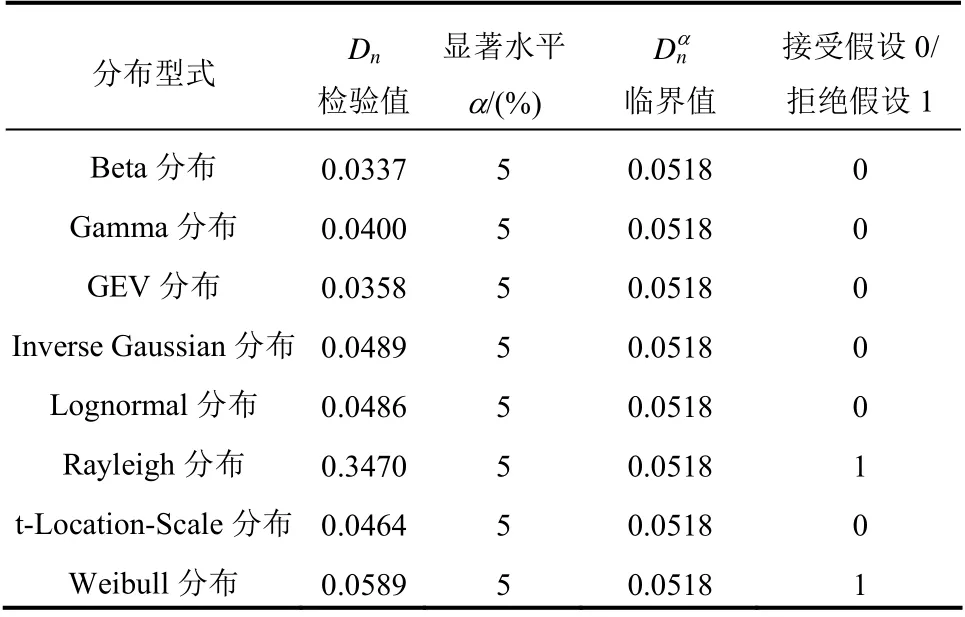
表4 無量綱沖擊荷載上升段持續時間各理論 概率分布K-S 檢驗結果 Table 4 K-S test results of different theoretical probability distributions of non-dimensional rise time

將 先 驗、后 驗 概 率 分 別 記 為P′ (Θ=θi)和P′(Θ=θi)，則式(2)可寫為：

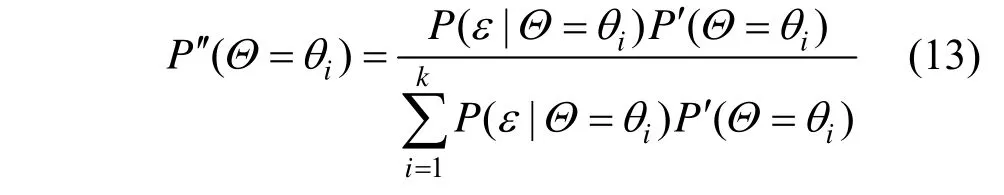
Θ的期望值即為參數θ的Bayes 估計結果：

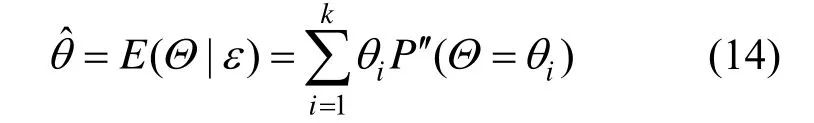
連續分布情況下，假設θ為連續隨機變量，其先驗概率密度函數為 ( )f θ′ ，則θ的先驗概率表達為P(θi＜θ＜θ i+Δθ) =f′(θ)Δθ，經觀測結果ε修正后，其后驗概率如下：

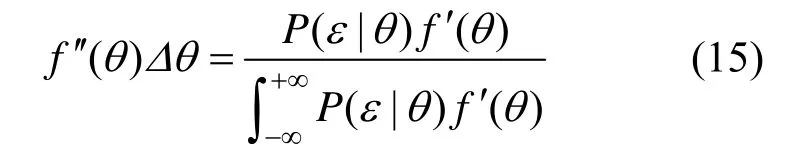
則參數θ經Bayes 更新后的估值如下：

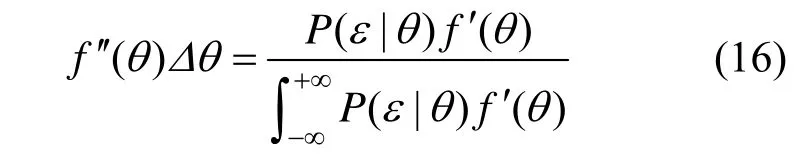
通常，后驗分布很難求得，數值方法常常是唯一可行和有效的方法。可采用Monte Carlo 模擬(MCS)進行大量模擬，最終得到后驗概率的近似分布。各Copula 函數參數估計值如表5 所示。

采用均方根誤差法(RMSE)、AIC 信息準則法、BIC 信息準則法對Copula 函數進行擬合優度評價，選取擬合度最高的Copula 函數。由表6 可知，FGM Copula 函數的擬合效果最佳，其函數形式如下：

式中，θ=-1 .0000。

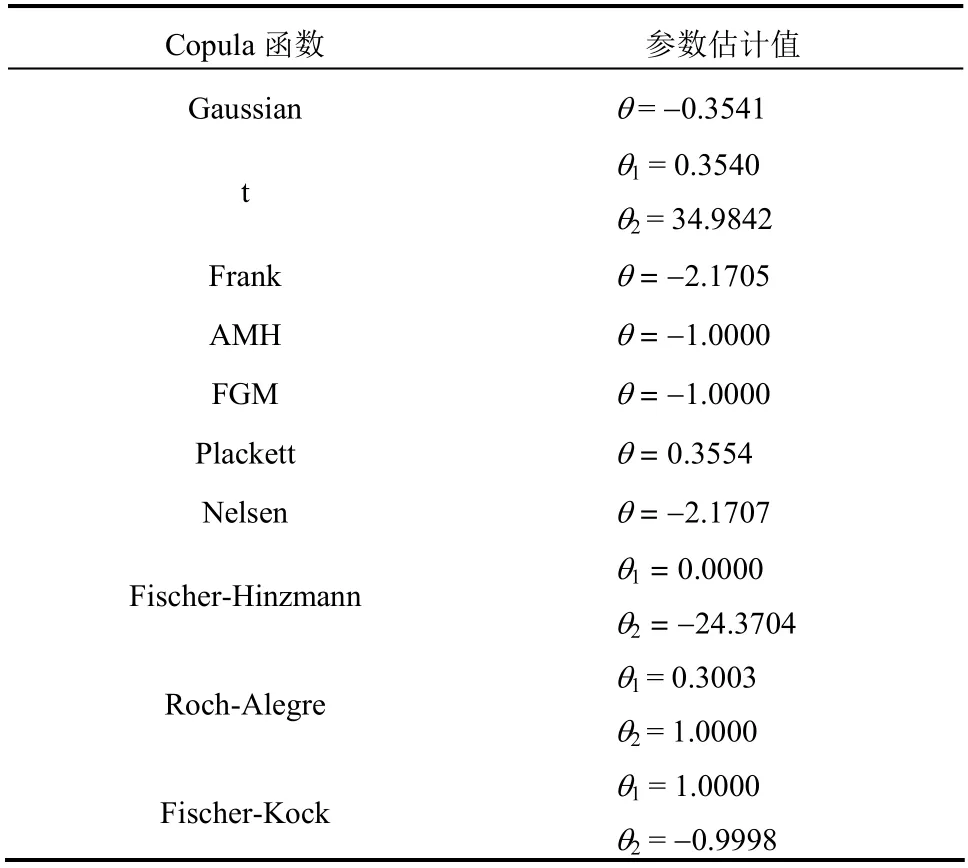
表5 各Copula 函數參數估計值 Table 5 Estimated value of each Copula function parameters

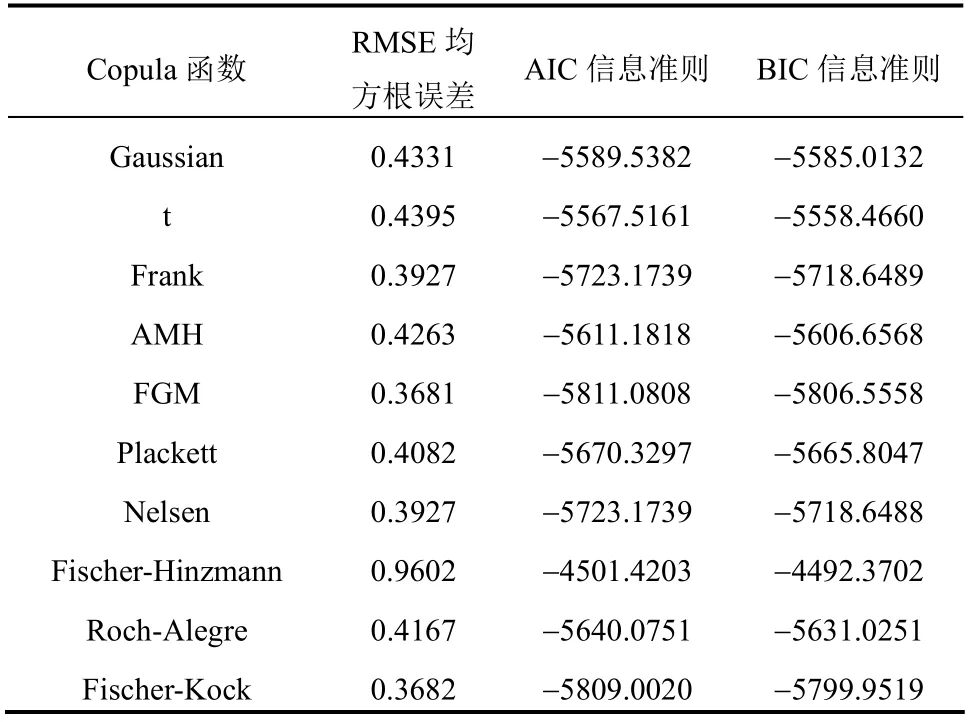
表6 各Copula 函數的擬合優度檢驗結果 Table 6 Test results of goodness of fit for different Copula functions

3.3 聯合概率分布

采用FGM Copula 函數建立無量綱沖擊荷載峰值與無量綱沖擊上升段持續時間的聯合概率模型。聯合概率密度和聯合概率分布如圖8 所示，聯合概率分布等值線如圖9 所示。

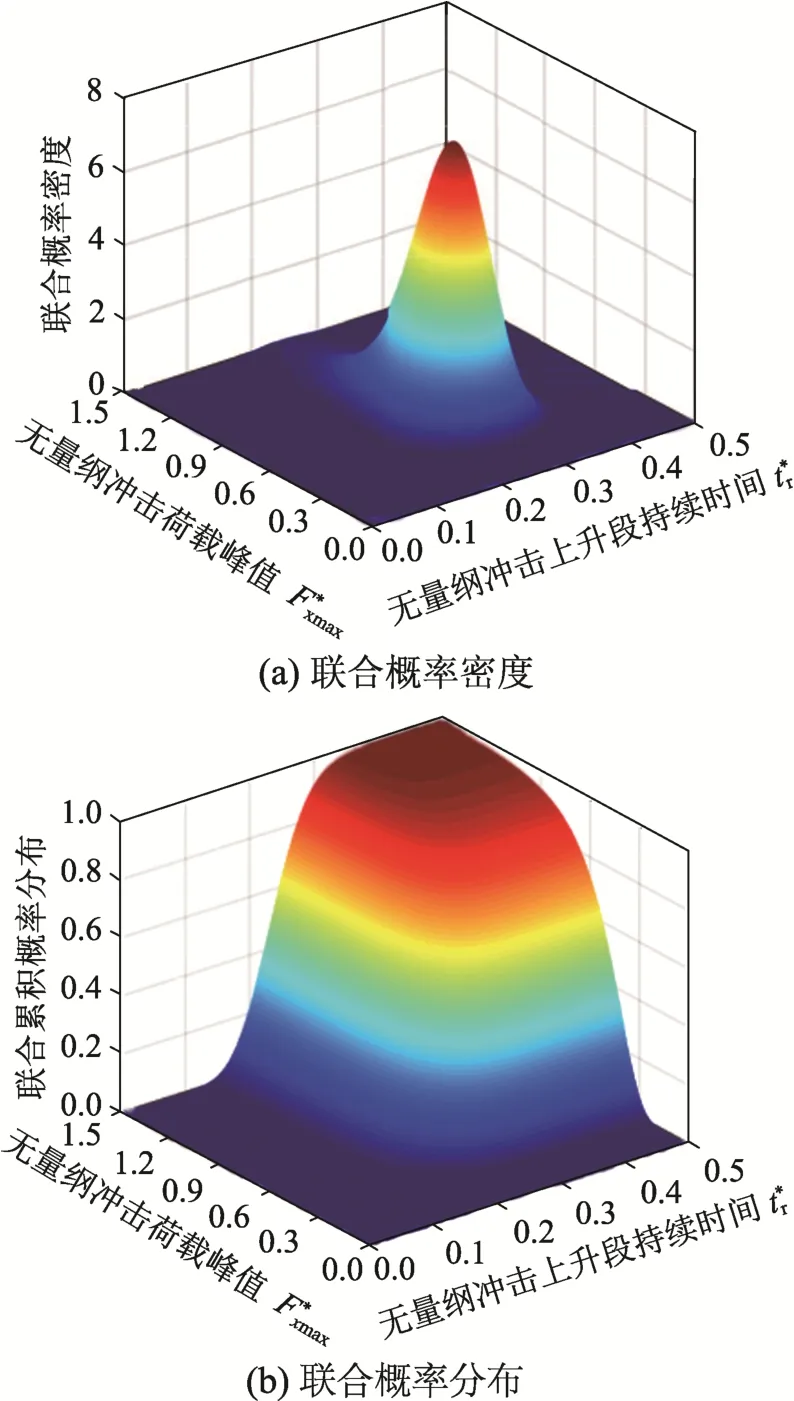
圖8 聯合概率密度及聯合概率分布 Fig.8 Joint probability density and joint probability distribution

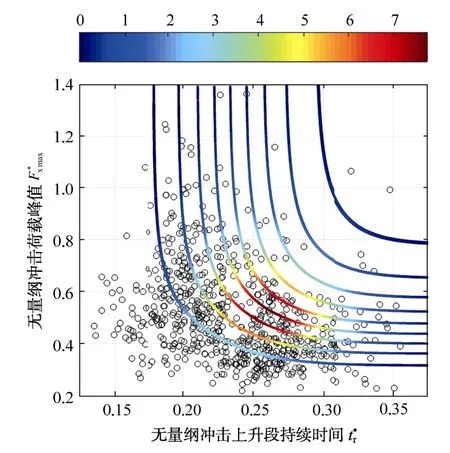
圖9 聯合概率分布等值線 Fig.9 Contour of joint probability distribution

圖8(a)表示在波浪條件和結構參數給定的情況下，不同的Fxmax和tr組合出現的概率，再通過波浪荷載時程模型，就可得到不同波浪沖擊荷載出現的概率。

由圖8(b)和圖9 可得，在波浪條件和結構參數給定的情況下，Fxmax和tr的組合在一個確定的累計概率下的取值范圍。Fxmax和tr在0.1～0.9 不同累計概率下的關系，均符合圖9 中對應的等值線。

4 結論

為研究極端波浪作用于高樁承臺時波浪沖擊荷載水平分量的時變規律，進行了以平潭海峽公鐵兩用跨海大橋為原型的尺縮模型水槽實驗。對試驗結果進行分析，提出了基于沖擊荷載峰值和沖擊上升段持續時間的波浪沖擊荷載時程模型。并對其中參數進行分析，為描述沖擊過程的隨機性、沖擊荷載峰值與沖擊上升段持續時間的關系，基于Copula理論，建立了聯合概率模型。主要得到了以下結論：

(1) 承臺底部凈空為0 cm、2 cm、4 cm 時，波浪沖擊荷載水平分量的時程呈現明顯的不對稱性，采用分段函數進行描述，其中上升段采用三角函數的組合形式，下降段采用冪函數形式。

(2) 波浪沖擊荷載具有明顯的隨機性，無量綱沖擊荷載峰值符合廣義極值分布，無量綱沖擊上升段持續時間符合Beta 分布。

(3) FGM Copula 函數能較好描述無量綱沖擊荷載峰值和無量綱沖擊上升段持續時間的聯合概率分布。

本研究探明了極端波浪作用下波浪沖擊荷載水平分量的時變特性，并對沖擊荷載峰值和沖擊上升段持續時間的隨機性進行描述。對高樁承臺的波浪荷載設計和結構動力分析具有重要價值。