基于多次碰撞源的屏蔽計算方法研究

王新宇，張 斌，陳義學

(華北電力大學 核科學與工程學院，北京 102206)

離散縱標(SN)方法是屏蔽計算中常用的算法之一[1]。在離散縱標屏蔽計算中，因對粒子輸運方程中空間變量和角度變量的近似處理，不可避免地存在離散誤差，特別是屏蔽計算中角通量密度在空間或角度上的分布不光滑甚至間斷的情況。射線效應是角度離散化造成的標通量密度呈現空間震蕩分布的現象，在帶有孔道、孤立點源的屏蔽問題中尤為明顯[2-3]。首次碰撞源方法[4-7]通過解析方法或高階方法求解點源產生的未碰撞角通量密度，計算出每個空間網格在離散方向上的首次碰撞源作為SN計算中的分布源。這樣即使在弱散射情況下，粒子也能運動到整個求解空間從而減小角度離散誤差。首次碰撞源方法雖能在一定程度上緩解射線效應，但無法解決空間離散導致的數值擴散問題，同時首次碰撞源方法難以處理二次射線效應[8]。對空間變量的離散易導致未碰撞通量密度的數值解出現數值擴散效應，具體表現為數值模擬中粒子的傳遞偏離真實的方向或粒子在傳遞過程中不能正確地衰減[9]。離散縱標屏蔽計算中的空間變量離散格式主要可分為有限差分格式[10]、短特征線格式[11]和間斷有限元格式[12]等，其中一些空間離散格式雖具備良好的魯棒性，但不能緩解因角度離散導致的射線效應。

本文基于射線追蹤研究一種半解析的多次碰撞源方法，以緩解射線效應和數值擴散對屏蔽計算精度的影響。通過計算在選定區域內粒子發生多次碰撞的通量密度，將粒子每次碰撞看作一個散射的過程。由每次碰撞通量密度(包括未碰撞通量密度)和散射截面計算出選定區域網格的多次碰撞源，將此分布源作為固定源對整個模型進行離散縱標輸運計算。然后將每次碰撞通量密度(包括未碰撞通量密度)和輸運求解的碰撞通量密度求和，得到整個計算模型的通量密度分布。

1 理論方法

1.1 多次碰撞源方法

穩態單群固定源無裂變輸運方程如下：

(1)

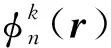
Lψ=Sψ+Q

(2)

L為輸運算子：

(3)

S為散射矩陣：

(4)

將整個模型分為區域A和區域B兩部分，假設選定計算粒子在區域A中碰撞多次的通量密度，區域A需包含源區。由此可得：

L(ψA+ψB)=(SA+SB)(ψA+ψB)+Q

(5)

其中：ψA和ψB分別為區域A和區域B中的通量密度，兩者之和表示整個模型內的角通量密度分布情況；SA和SB分別為區域A和區域B中的散射矩陣，兩者之和表示整個模型內的散射矩陣的分布。在區域A內的ψB根據其物理意義均等于0，此時源區對區域A的通量密度占主要貢獻，將式(5)進行化簡后可得到：

LψA=SψA+Q

(6)

式(6)描述粒子在區域A運動的過程，區域B的通量密度來自區域A的通量密度的貢獻，即在后續計算中將區域A看作模型的源區，式(5)、(6)聯立后可得式(7)：

LψB=SBψA+(SA+SB)ψB=SBψA+SψB

(7)

由式(6)可得：

(8)

(9)

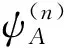
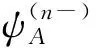
LψSN=SψSN+Q(n+1)

(10)

最終，由兩步輸運結果之和得到總通量密度，即：

(11)

多次碰撞源方法的主要思想在于將粒子每次發生碰撞的過程獨立處理，與標準的SN方法的源迭代求解流程有所區別。在計算粒子每次發生碰撞的過程時采用半解析的射線追蹤方法[13]，盡量減少因角度離散和空間離散引起的離散誤差，更準確地描述粒子在模型內的輸運行為。多次碰撞源方法具有一些積分輸運方法的性質。當選定的計算區域和碰撞次數均取極限值，即是計算整個模型內粒子碰撞無窮次后的通量密度分布情況，與標準的SN方法的源迭代求解流程所描述的物理過程一致。

1.2 求解流程

標準的SN方法求解方法是對群內散射源進行迭代計算，迭代方程如下：

(12)

(13)

其中：D為離散角度轉化為矩的算符；φ(l)為通量矩；ε為迭代的收斂準則。令迭代初始值φ(0)=0，ψ(n)即為至多經歷n次碰撞的粒子角通量密度。在源迭代過程中得到的ψ(0)，ψ(1)，…，ψ(n)分別為粒子未經碰撞的角通量密度，經1次碰撞的角通量密度，…，經n次碰撞的角通量密度。

選取Kobayashi基準題模型Ⅱ[14]分析迭代過程中模型內的通量密度分布情況。Kobayashi基準題模型Ⅱ的幾何結構如圖1所示。源強S和截面信息列于表1。

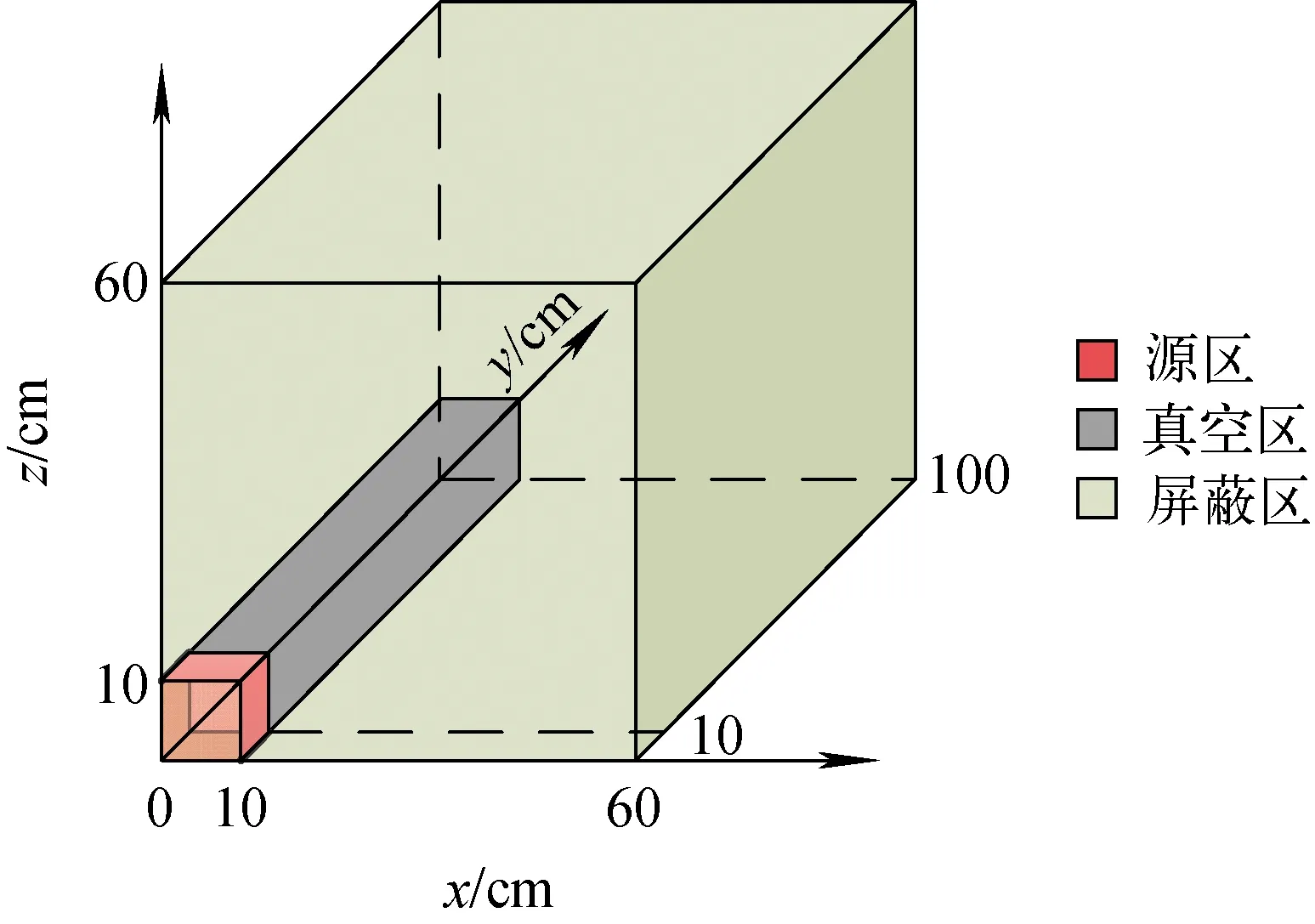
圖1 Kobayashi基準題模型Ⅱ幾何示意圖Fig.1 Geometry of Kobayashi benchmark problem model Ⅱ

表1 源強與截面信息
Table 1 Source strength and cross section

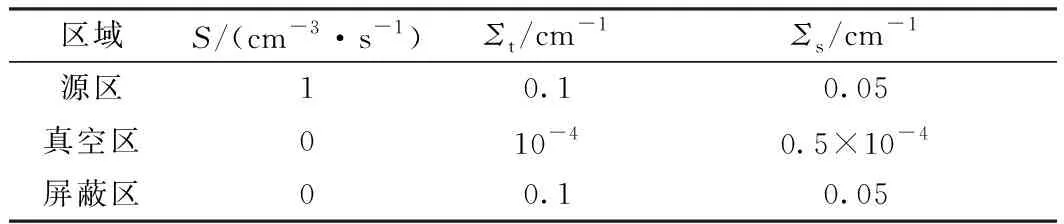
區域S/(cm-3·s-1)Σt/cm-1Σs/cm-1源區10.10.05真空區010-40.5×10-4屏蔽區00.10.05

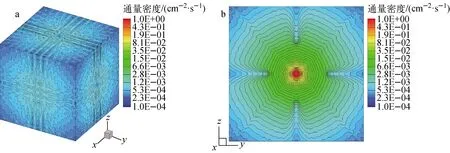
為盡可能減少離散誤差的影響，將模型劃分為步長為1 cm的60×100×60的空間網格集合，空間離散格式選擇置零修正的菱形差分格式，采用100階勒讓德-切比雪夫求積組進行計算，圖2為當源迭代過程進行到第n次時，模型內ψ(n)的分布情況。

從分布形狀上看，在初始幾次迭代中標通量密度在空間上分布呈現非物理振蕩，而隨后的散射過程會使整個模型空間內的標通量密度的分布趨于光滑，標通量密度的分布是隨著迭代的進行越來越廣且各向同性越來越強的，其非均勻性逐漸減弱。數值結果表明，對于帶有孔道的屏蔽問題，前幾次迭代的標通量密度數值上相對較大且主要分布在孔道內，隨著迭代的進行標通量密度逐漸減小。因此僅在計算未碰撞通量密度和前n次碰撞通量密度時采用半解析的射線追蹤方法，后續的碰撞通量密度采用SN方法求解：

圖2 Kobayashi基準題模型Ⅱ內通量密度分布示意圖Fig.2 Flux density distribution in Kobayashi benchmark problem model Ⅱ

(14)

其中：ψ(i)為粒子第i次碰撞的通量密度；Q(i)為粒子第i次碰撞時的源項。射線追蹤方法主要在于計算粒子在幾何空間中從ro點穿行到rp點的徑跡長度，即光學距離τ(ro,rp)，其表達式如下：

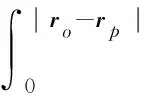
(15)

其中：μ為粒子運動方向的角余弦；Σt(ro+μΩrp)為ro+μΩo→p位置點的總截面，Ωo→p是從ro點穿行到rp點的單位向量。根據角通量密度的球諧矩定義：

(16)

碰撞角通量密度的球諧矩可由式(14)和式(16)確定：

(17)

采用多次碰撞源方法計算粒子在整個模型空間內碰撞無窮次的情況時，總通量密度ψtotal的迭代求解流程如式(18)所示，表現出多次碰撞源方法的積分性質。

Lψ(1)=Q,Sψ(2)=Sψ(1),…,Lψ(n)=Sψ(n-1)

(18)

2 基準驗證

2.1 自設屏蔽問題

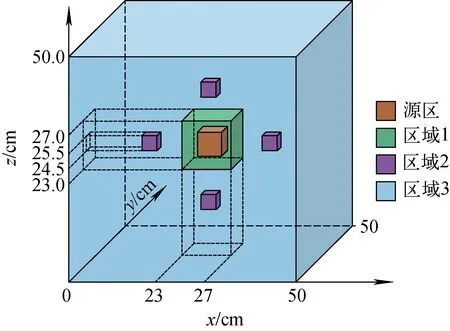
圖3 自設屏蔽問題幾何模型Fig.3 Geometric model of self-designed shielding problem

該自設屏蔽問題幾何模型如圖3所示，尺寸為50 cm×50 cm×50 cm，邊界條件均為真空邊界；源區位于模型中心邊長為2 cm的立方體，中子源強為1 cm-3·s-1；源區外圍是一層尺寸為4 cm×4 cm×4 cm的高散射比材料；屏蔽層內分布著4個總截面較大的立方體塊，尺寸為1 cm×1 cm×1 cm。具體的截面信息列于表2。

表2 自設屏蔽問題的截面信息Table 2 Cross section of self-designed shielding problem

該問題源區的四周分布有總截面相對較大的高散射比單元，因射線效應形成的粒子束穿過這些單元時可能會導致新的或次要的射線效應，采用首次碰撞源方法修正不能消除由這些單元產生的二次射線效應，需更高次的碰撞源修正方法。

整個模型被劃分為步長1 cm的50×50×50空間網格集合，采用16階勒讓德-切比雪夫求積組，置零修正的菱形差分格式。分別使用標準SN方法、首次碰撞源方法和多次碰撞源方法計算通量密度分布，其中多次碰撞源方法的計算區域為源區和區域1，碰撞次數為2次。3種方法的計算時間分別為26、25和26 s，計算結果如圖4～6所示，首次碰撞源方法在一定程度上緩解了離散誤差，但射線效應依然十分明顯，而多次碰撞源方法減弱二次射線效應的效果更加顯著。

2.2 Kobayashi基準題模型Ⅲ

Kobayashi基準題是經濟合作和發展組織核能機構(OECD/NEA)輻射輸運專家組提出的用于驗證輸運程序屏蔽計算能力的基準題。選取Kobayashi基準題模型Ⅲ，用標準SN方法、首次碰撞源方法和多次碰撞源方法分別進行計算，分析多次碰撞源方法的計算精度、計算效率及離散誤差的消除效果。

a——整體模型；b——y=25 cm平面圖4 SN方法計算的通量密度分布Fig.4 Flux density distribution calculated by SN method

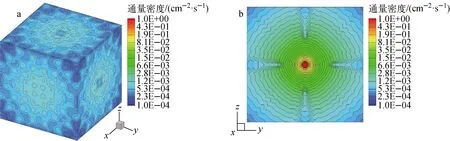
a——整體模型；b——y=25 cm平面圖5 首次碰撞源方法計算的通量密度分布Fig.5 Flux density distribution calculated by first collision source method

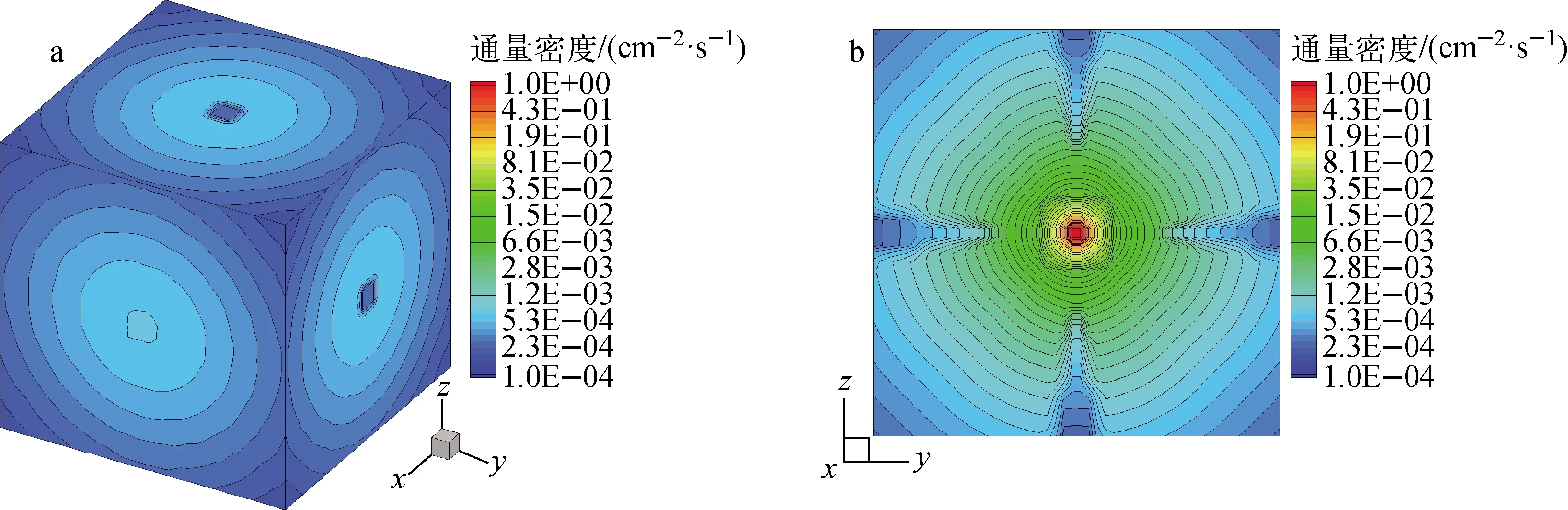
a——整體模型；b——y=25 cm平面圖6 多次碰撞源方法計算的通量密度分布Fig.6 Flux density distribution calculated by n’th collision source method

該模型是一個具有折線形孔道的深穿透屏蔽問題，幾何模型如圖7所示。孔道內的角通量密度分布呈現強各向異性，且孔道與屏蔽區交界面處的通量密度梯度極大，存在較大的離散誤差。源強與截面信息列于表1，選取基準報告中提供的沿孔道的22個坐標點作為關鍵點輸出。

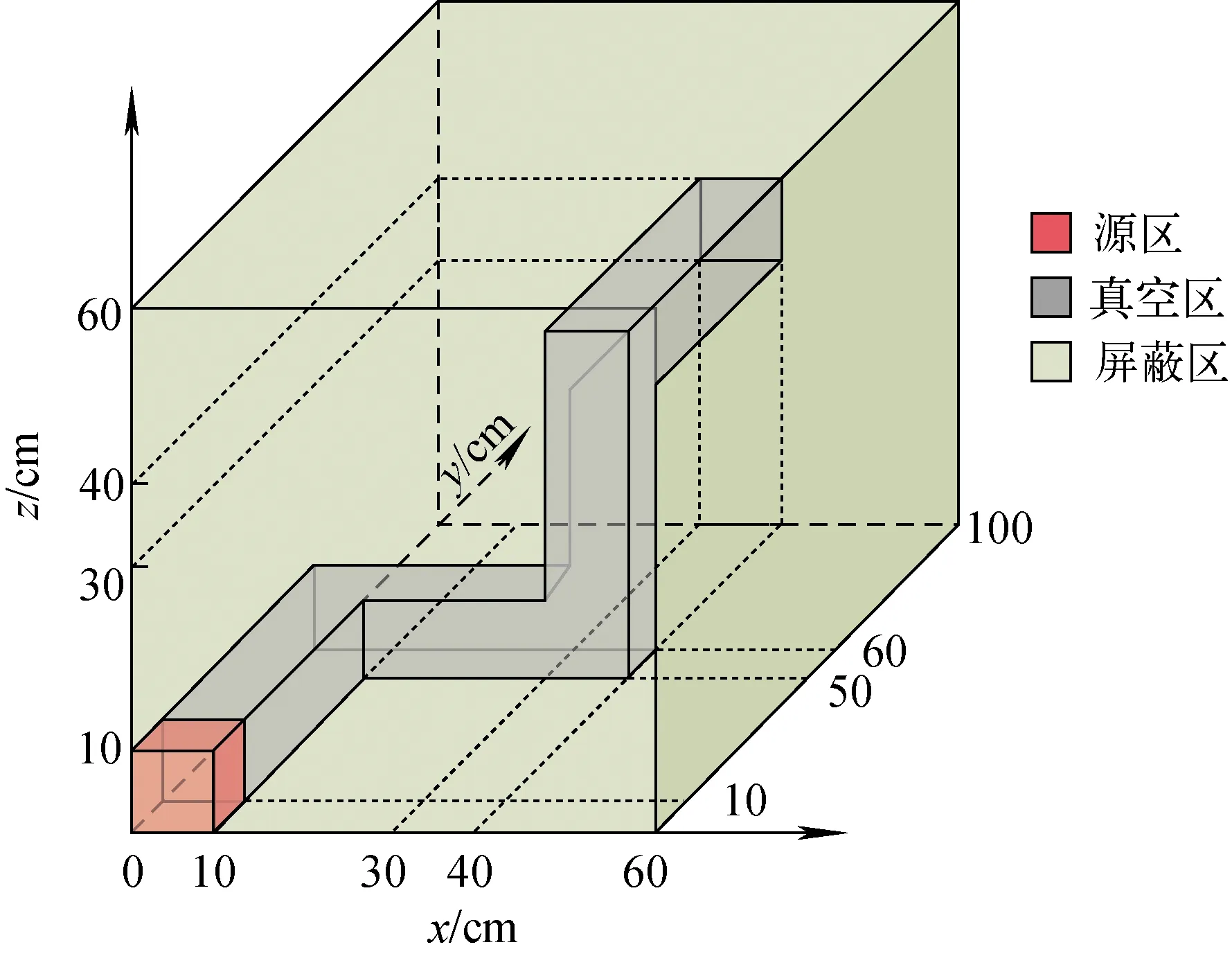
圖7 Kobayashi基準題模型Ⅲ幾何示意圖Fig.7 Geometry of Kobayashi benchmark problem model Ⅲ

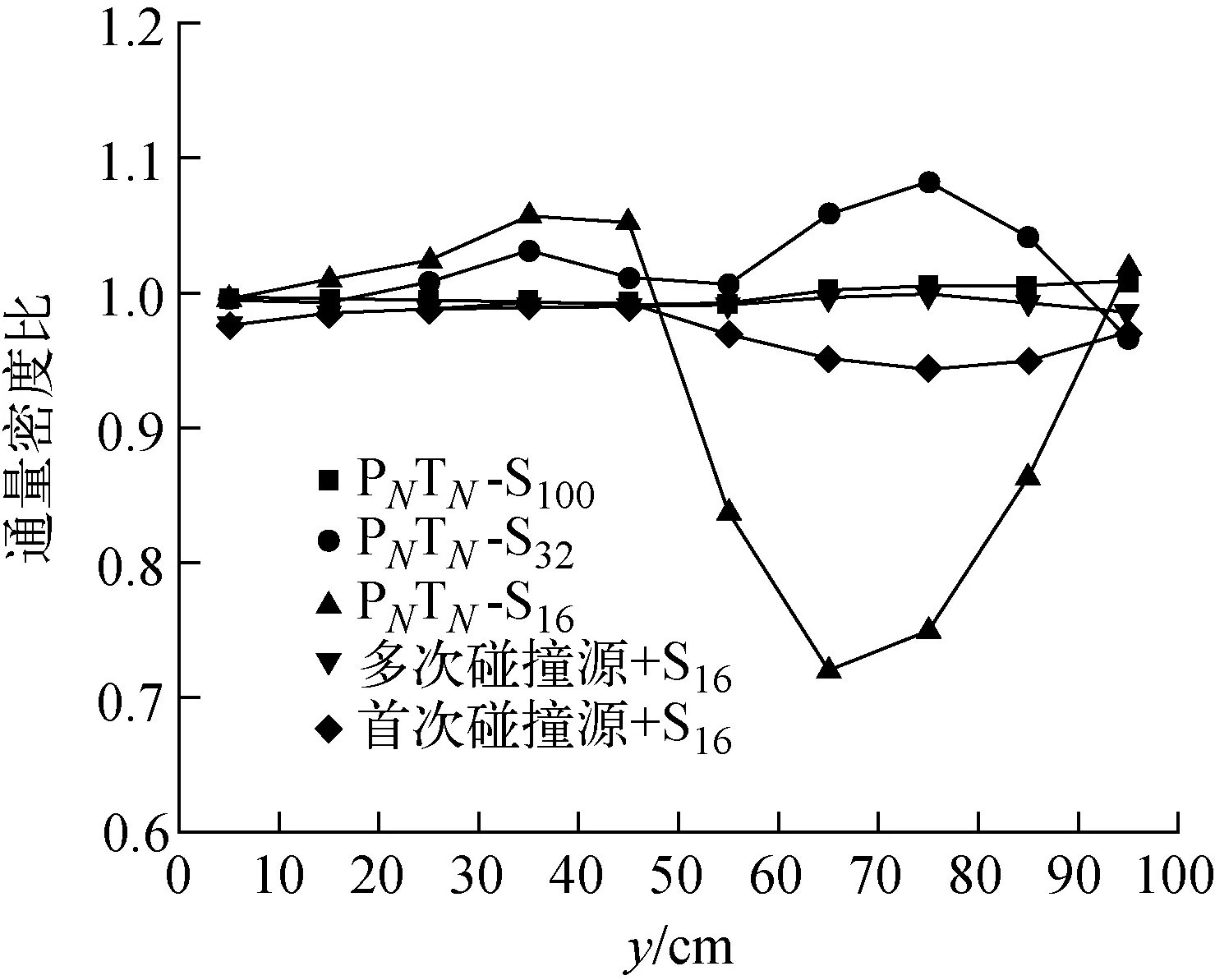
圖8 Kobayashi基準題模型Ⅲ關鍵點通量密度計算值與基準值之比Fig.8 Ratio of calculated value and benchmark value in Kobayashi benchmark problem model Ⅲ

模型劃分為步長2 cm的30×50×30空間網格集合，選取置零修正的菱形差分格式，迭代收斂準則為1×10-4。以基準報告中提供的蒙特卡羅程序計算結果作為參考值，分別采用SN方法、首次碰撞源方法和多次碰撞源方法的計算值與參考值進行比較，其中多次碰撞源方法的計算區域為源區和屏蔽區，碰撞次數為2次，沿y軸關鍵點的相對誤差變化曲線如圖8所示。數值結果表明，孔道的存在導致角通量密度的各向異性程度隨距離增加而增強。當采用16階勒讓德-切比雪夫求積組計算時，孔道內的中子通量密度非物理震蕩強烈；當求積組的階數提高，采用100階PNTN求積組進行計算，通量密度的相對誤差隨距離的增加仍呈現逐漸上升的趨勢。采用首次碰撞源方法計算時，同樣使用16階PNTN求積組計算得到的相對誤差整體小于10%，但離散誤差的影響并未完全消除。另一方面，由于射線追蹤的性質，首次碰撞源方法低估了源區附近的未碰撞通量密度。采用多次碰撞源方法計算時，使用16階PNTN求積組計算結果的相對誤差整體小于5%，相對誤差的均方根和標準差均有所降低，多次碰撞源方法也存在低估源區附近通量密度的問題。

表3列出了16階PNTN求積組、首次碰撞源方法和多次碰撞源方法的計算值與參考值的相對誤差和計算時間。數值結果表明，多次碰撞源方法的相對誤差均方根小于3%，相對誤差的標準差為1.025 2×10-2，消除離散誤差的能力優于另外兩種計算方法，但計算效率方面，相同情況下多次碰撞源方法的計算耗時較長，原因主要是多次碰撞源方法計算多次碰撞通量密度時，需對所選區域的每個網格進行射線追蹤，因此多次碰撞源方法的計算量與所選計算區域的網格數密切相關。

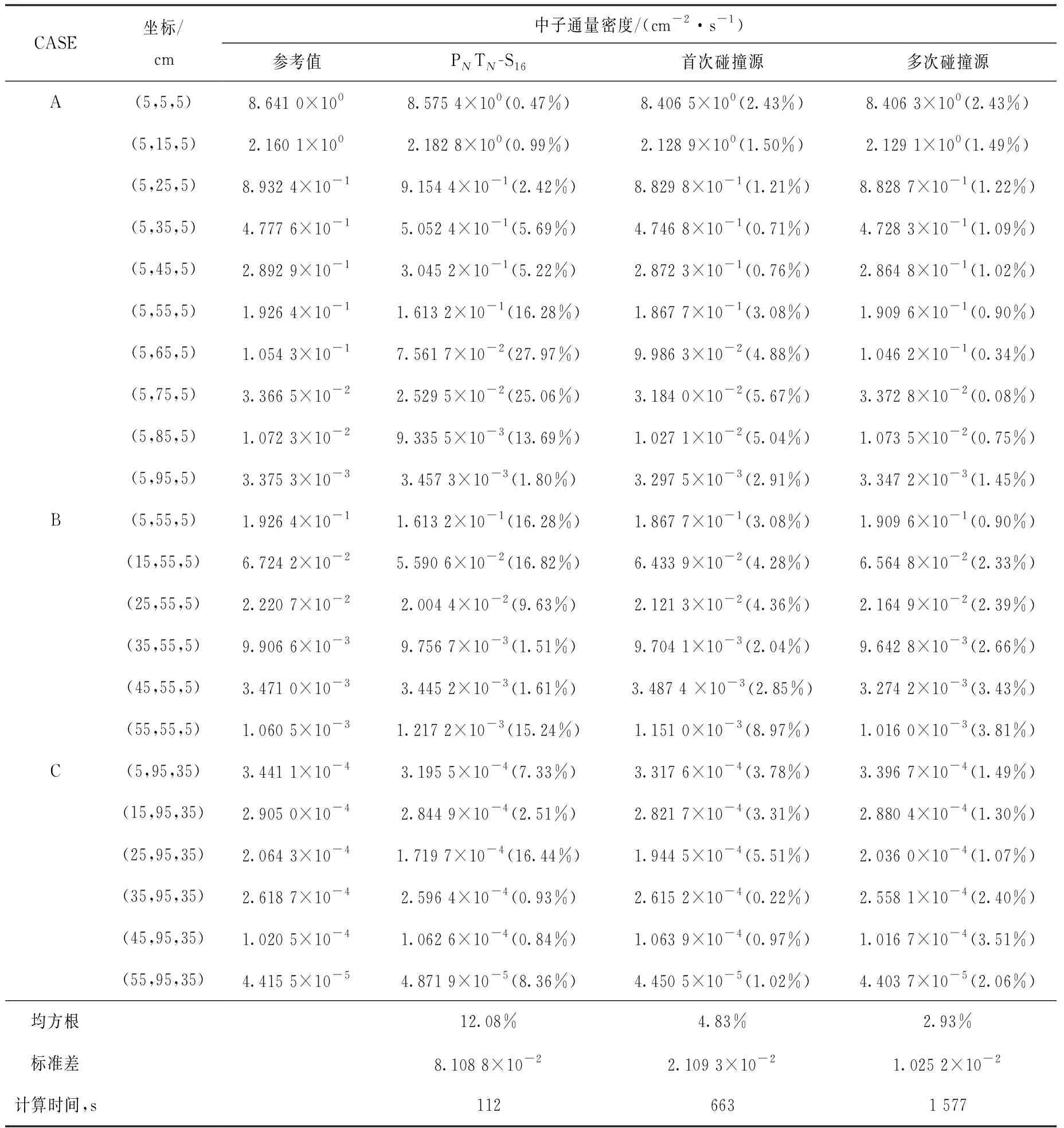
表3 Kobayashi基準題模型Ⅲ計數點位中子通量密度Table 3 Neutron flux density at key point for Kobayashi benchmark problem model Ⅲ

注：括號內為相對誤差

2.3 自設多群固定源問題

為了分析多次碰撞源方法對多群屏蔽問題的計算精度，自設均勻介質固定源問題。該自設問題幾何模型如圖9所示，尺寸為10 cm×10 cm×10 cm，邊界條件均為真空邊界，材料為304不銹鋼[15]；源區位于模型中心為邊長1 cm的立方體，中子源強為1 cm-3·s-1，能量為14 MeV。計算采用30群的MATXS-10截面庫，各向異性散射P3階展開，網格尺寸為0.25 cm，100階PNTN求積組的計算結果作為參考解。

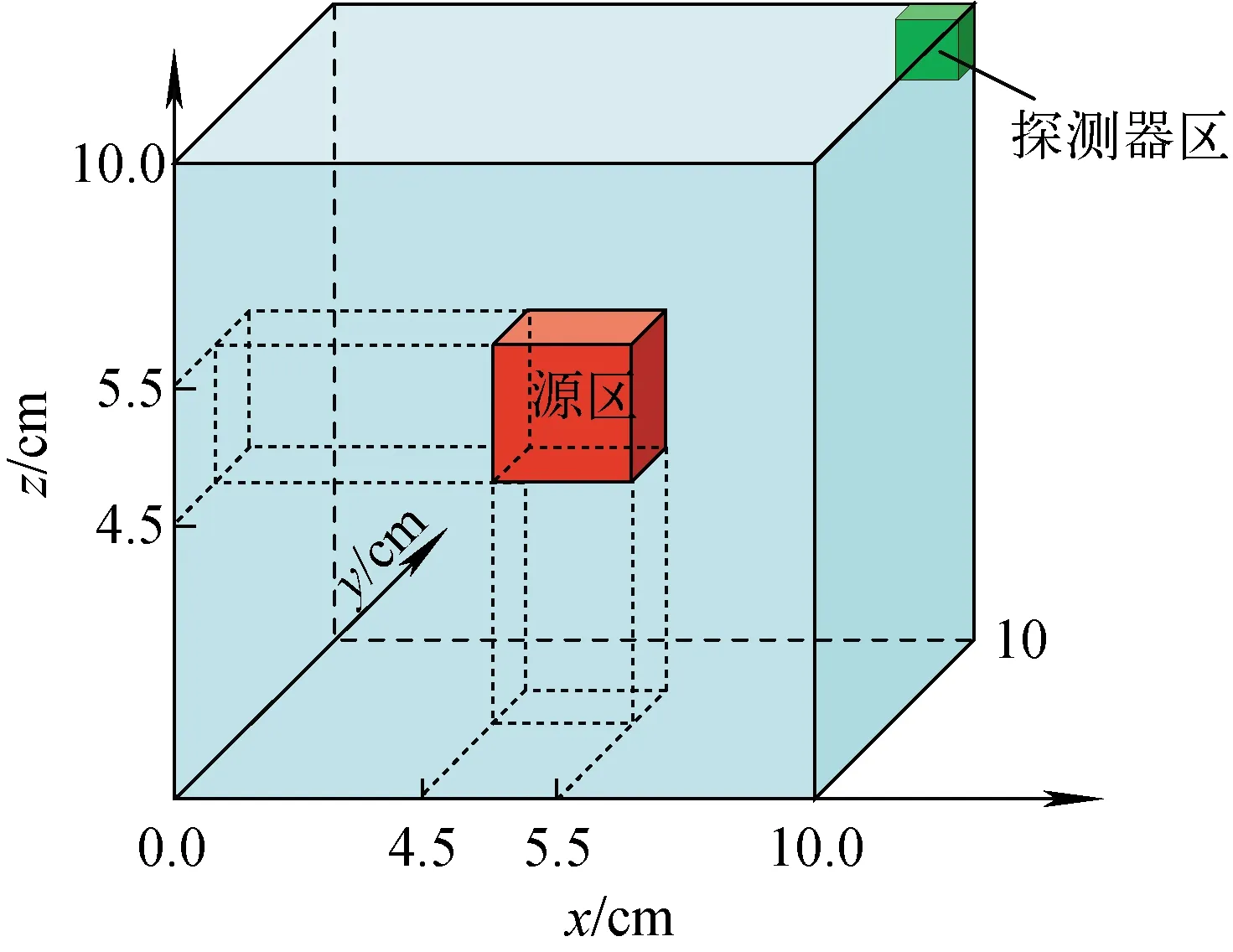
圖9 固定源問題幾何模型Fig.9 Geometric model of fixed-source problem

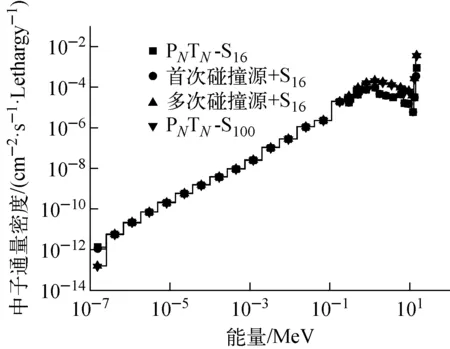
圖10 探測器中子能譜Fig.10 Neutron spectrum of detector

圖10為標準SN方法、首次碰撞源方法和多次碰撞源方法在探測器處的能譜結果，其中多次碰撞源方法的計算區域為整個模型區域，碰撞次數為2次，且僅在第2群(13.5～15 MeV)使用多次碰撞源方法。在能量較低的能量區間內各種方法的計算結果與參考解相近，但在0.1 eV～14 MeV能量區間內僅有多次碰撞源方法與參考解吻合較好。這是由于高能部分的群內散射截面較小同時各向異性散射較強，導致能量最高能群的角通量密度分布各向異性程度最強，第2群的角度離散誤差最大，射線效應最嚴重。而隨著粒子的慢化，較低能量能群的角通量密度各向異性程度減弱。通過比對計算，驗證了多次碰撞源方法可有效減弱離散誤差，具有較高的可靠性。

表4列出不同條件下的計算時間，多次碰撞源方法的計算時間與16階PNTN求積組和首次碰撞源方法的計算時間相比耗時較長。綜合計算精度考慮，多次碰撞源方法相較于100階PNTN求積組，兩者精度相近，計算時間的加速比為3.49。

表4 不同條件下的計算時間Table 4 Calculation time of different conditions

3 結論

針對屏蔽計算中強非均勻效應造成離散誤差過大的問題，研究了基于射線追蹤技術的多次碰撞源方法。多次碰撞源方法通過射線追蹤計算指定區域網格內粒子碰撞多次的通量密度，將孤立源等效為模型內的分布源，在求積組階數較低時仍可得到準確的結果，有效地消除了離散誤差對屏蔽計算精度的影響。數值計算結果表明，多次碰撞源方法相比首次碰撞源方法具有消除次級射線效應的能力，且能緩解因離散誤差導致的射線效應和數值擴散現象。