初中數學變式訓練常用方法略論

尹慧梅

對于初中數學尤其是對于九年級畢業班的總復習教學而言，時間緊、任務重、要求高，如何提高數學總復習的質量和效益，是每位數學教師必須面對的問題。如何去進行習題訓練才能在有限的時間內高質量完成我們的教學目標呢？如何去復習才能讓學生適應“出活題，考思維、測能力”新形勢下的要求呢？如何去訓練才能使學生做到觸類旁通，具有“舉一反三”之力呢？帶著這些問題，本人堅持不懈地研究、對比、分析近幾年各地中考卷，發現每次都會產生一種似曾相識和恍然大悟的感覺：變式在中考試題命制中無處不在。因此，現就初中數學變式訓練問題展開探討，希望能夠以此為相關教育工作者提供一些參考和建議。

中考試題之間通過變式產生的似曾相識，引發了筆者對初中數學變式訓練的思考。如何在有限的時間讓學生得分最大化？這就要求教師在日常的習題訓練中講究策略，讓學生在考場上能產生似曾相識的感覺，解題方法信手拈來，從而達到答題又快又準。很多老師認為，學生腦海中解題方法的產生，屬于“靈光乍現”，有自發性和隨機性，老師是無能為力的。但事實上，解題方法的得來絕對不是無緣無故。波利亞在“怎樣解題表”中曾這樣提出：“你知道一個與此相關的問題嗎”;“試想出一個具有相同或相似未知數的熟悉的問題”;“你見過相同的題目或形式稍有不同的問題嗎”。由此可知，解題思路的形成，解題方法的獲得與解題者的知識儲備、解題經驗的積累關系很大。例如從2015年四川內江第27題（3）問中“最小”出發，有人聯想到平時“將軍飲馬模型”，有的人想方設法構造300角直角三角形，有人努力構造相似三角形......這其實就是“似曾相識”誘發解題方法。那么學生如何能產生似曾相識的感覺？這其實應當成為教學在日常教學過程中思考的重點。本文通過一道具體案例闡述了如何真正實現有效的變式訓練，讓學生做到觸類旁通，舉一反三。

1 例題分析

下面以2013江蘇揚州18題和2014浙江寧波18題為例

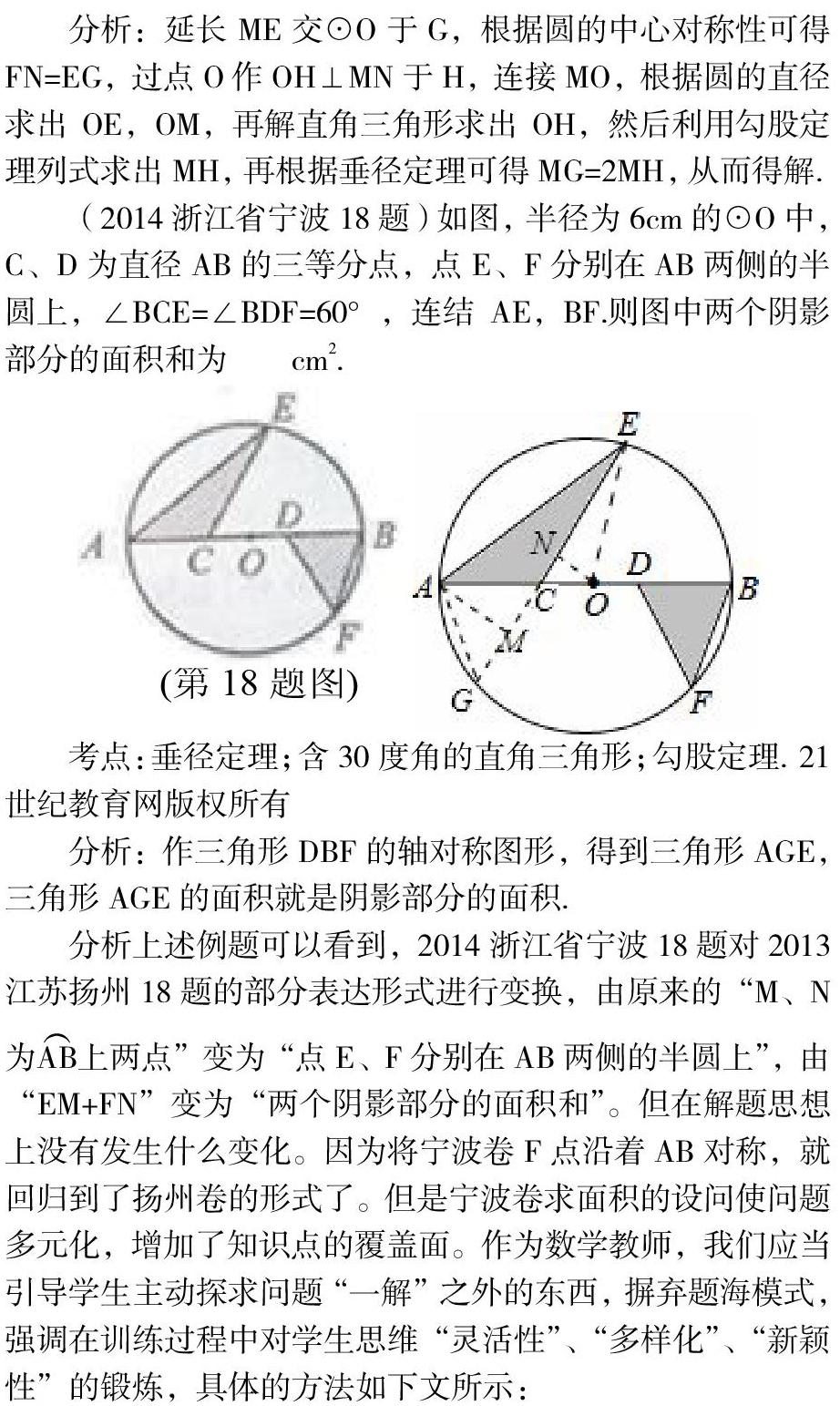
（2013江蘇揚州18題）如圖，已知⊙O的直徑AB=6，E、F為AB的三等分點，M、N為上兩點，且∠MEB=∠NFB=60°，則EM+FN=.

考點：垂徑定理;含30度角的直角三角形;勾股定理.

分析：延長ME交⊙O于G，根據圓的中心對稱性可得FN=EG，過點O作OH⊥MN于H，連接MO，根據圓的直徑求出OE，OM，再解直角三角形求出OH，然后利用勾股定理列式求出MH，再根據垂徑定理可得MG=2MH，從而得解.

（2014浙江省寧波18題）如圖，半徑為6cm的⊙O中，C、D為直徑AB的三等分點，點E、F分別在AB兩側的半圓上，∠BCE=∠BDF=60°，連結AE，BF.則圖中兩個陰影部分的面積和為??cm2.

考點：垂徑定理;含30度角的直角三角形;勾股定理.21世紀教育網版權所有

分析：作三角形DBF的軸對稱圖形，得到三角形AGE，三角形AGE的面積就是陰影部分的面積.

分析上述例題可以看到，2014浙江省寧波18題對2013江蘇揚州18題的部分表達形式進行變換，由原來的“M、N為上兩點”變為“點E、F分別在AB兩側的半圓上”，由“EM+FN”變為“兩個陰影部分的面積和”。但在解題思想上沒有發生什么變化。因為將寧波卷F點沿著AB對稱，就回歸到了揚州卷的形式了。但是寧波卷求面積的設問使問題多元化，增加了知識點的覆蓋面。作為數學教師，我們應當引導學生主動探求問題“一解”之外的東西，摒棄題海模式，強調在訓練過程中對學生思維“靈活性”、“多樣化”、“新穎性”的鍛煉，具體的方法如下文所示：

2 初中數學變式訓練的基本思路分析

2.1 綱舉目張，以不變應萬變——通過圍繞四基四能提升訓練有效性

《2017初中畢業升學考試說明》指出：“數學考試著重考查七至九年級數學的基礎知識、基本技能、基本思想、基本活動經驗，以及發現問題、提出問題、分析問題、解決問題的能力。”所以中考復習課上，教師要以四基四能為綱，以具體教學內容為目，重視對數學基礎知識講解、基本技能的培養、基本思想的總結、基本活動經驗的積累、基本模型的提煉。訓練過程要發散徹底，聚焦到位，以發展能力為目的，注重通性通法，保證學生在課堂上夯實基礎，碰到問題能夠洞察秋毫，發現似曾相識，以不變應萬變，轉化未知為已知。

2.2 見招拆招，以變應變——通過變式訓練提升教學有效性

變式訓練立足于學生現有的知識水平，在學生的最近發展區內，設計一些列逐次遞進的問題。以學生熟悉的知識為起點，解決更為一般的數學問題，實現學生現有能力和學生潛力之間的跨越。《新課程標準》指出“人人學有價值的數學;人人都能獲得必需的數學;不同的人在數學上得到不同的發展。”所以教師在數學中考復習課中，可以采用一題一課的模式，從易到難，遞進變式，通過一題多變、一題多問、一題多解、多題歸一，有意識地引導學生分層學習，以變應變，從“變”的現象中發現“不變”的本質，從“不變”的本質中探求“變”的規律，促進學生適應形異而實同的數學中考試題，練就透過現象看本質的火眼金睛，培養學生發現似曾相識的能力。

3 結語

布魯納說：“學習不但應該把我們帶往某處，而且還應該讓我們日后的繼續前進更容易。” 為了學生的可持續發展，筆者將繼續探索初中數學試題的特點，進一步優化變式訓練的模式，讓學生在課堂上打好基礎，閱盡千變萬化，積累解題經驗，從而能面對考試，胸有“似曾相識題”，有備無患！

（作者單位：興義市陽光書院）