含凹坑缺陷的推進劑儲存容器安全性評價*

劉宗虎，王富強

(西安航天動力試驗技術研究所，陜西 西安 710100)

推進劑貯存容器存放的介質(偏二甲肼)具有劇毒、腐蝕、易燃等特點，一旦泄漏，會給人員、裝備造成重大損失，使用時必須經常進行氣密性檢測與安全性評估[1-3]。從實驗和長期使用現場數據來看，設備在制造、安裝過程中，由于操作不當，一些因素，如裂紋(表面裂紋、內埋裂紋和半露頭裂紋)、變形等嚴重影響其安全使用。胡寬等[4]考慮到貯存容器材料性能、受力、強度和裂紋初始尺寸等參數的隨機性，建立了推進劑貯存容器概率安全評定壽命預測模型，研究表明比確定性的標準評定更為合理。袁杰紅等[5]通過對推進劑貯箱結構的合理簡化，將線彈簧模型應用于未穿透裂紋應力強度因子的求解，不僅能求解表面裂紋問題，還能求解內埋裂紋和半露頭裂紋問題，該方法與傳統的數值方法比較，大大減少了編程和計算量，更加適合于工程實際應用。眾多學者從裂紋角度對推進劑儲存容器進行了安全性分析，而實際中由于吊裝或搬運過程中容器的變形也成為不容易發覺的潛在安全隱患，容易被忽視。因此，作者利用ANSYS有限元分析軟件對西安航天推進技術研究所試驗基地的含有凹坑缺陷的推進劑貯存容器進行安全性分析，并對殼體中的等效應力進行研究，進一步為推進劑貯存容器的安全使用提供理論指導。

1 儲存容器性能參數

推進劑儲存容器為圓柱型儲罐，在運輸安裝過程中，由于外力作用，在筒體接近封頭位置出現變形，形成凹坑，凹坑缺陷直徑D≈600 mm，凹坑缺陷深度h=50 mm，推進劑儲存容器材料為不銹鋼0Cr18Ni9Ti，其他主要參數見表1。

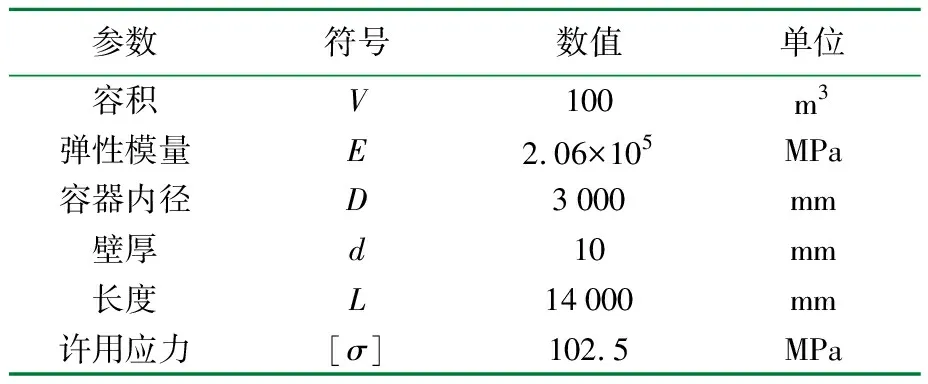
表1 推進劑儲存容器基本參數

2 有限元模型建立

采用ANSYS Workbench14.5進行建模，在承受壓力時，其缺陷附近出現應力集中現象，導致該區域有出現最先被破壞的趨勢，所以在進行模擬分析時一般都是選取包含缺陷區域容器的一部分進行研究，課題在模擬中選取缺陷形狀為球形模型。查閱相關文獻，為了消除邊界效應，根據圣維南原理[6-7]，有限元模型的長度取容器直徑的3～5倍，在進行有限元模擬分析時選取儲存容器模型的 1/2進行模擬分析研究。為了對比分析，建立了不含和含有凹坑缺陷時的儲存容器模型，見圖1和圖2。

圖1 不含凹坑模型

圖2 含有凹坑模型

選擇三維八節點六面體SOLID45單元模型進行網格劃分，缺陷處會出現應力集中現象，分析的重點應該在缺陷及周邊處，該區域加大網格劃分密度，提高有限元分析的準確性[8]。

由于推進劑儲存容器均為圓柱形，因此容器完全對稱，邊界條件選擇時，一端進行軸向位移約束，縱向對稱兩界面施加對稱約束，容器另一端界面施加載荷約束，實際容器所受的載荷主要為內壓和彎矩，其他載荷對管道影響很小，可以忽略，在分析中只考慮0.2 MPa內壓作用。

失效判定應該依照失效準則進行判定，而失效模式很大程度上決定了失效準則的選擇。對儲存類容器的失效模式，大多認為是局部塑形失效，也就是說在缺陷區域內，若有任一點達到管道的屈服強度，管道就意味著失效。容器是否失效可參照塑性失效準則，腐蝕缺陷區的最小等效應力應按第四強度理論確定極限壓力，見公式(1)[9]。

≤[σ]

(1)

式中：σ1、σ2、σ3為三方向的主應力，MPa；σvmes為等效應力，MPa；[σ]為材料的許用應力，MPa。

3 儲存容器有限元分析

3.1 不含凹坑缺陷壓力容器有限元分析

對不含凹坑壓力容器進行有限元分析，用來對比凹坑及補強的結果。容器外壁的應力云圖見圖3。

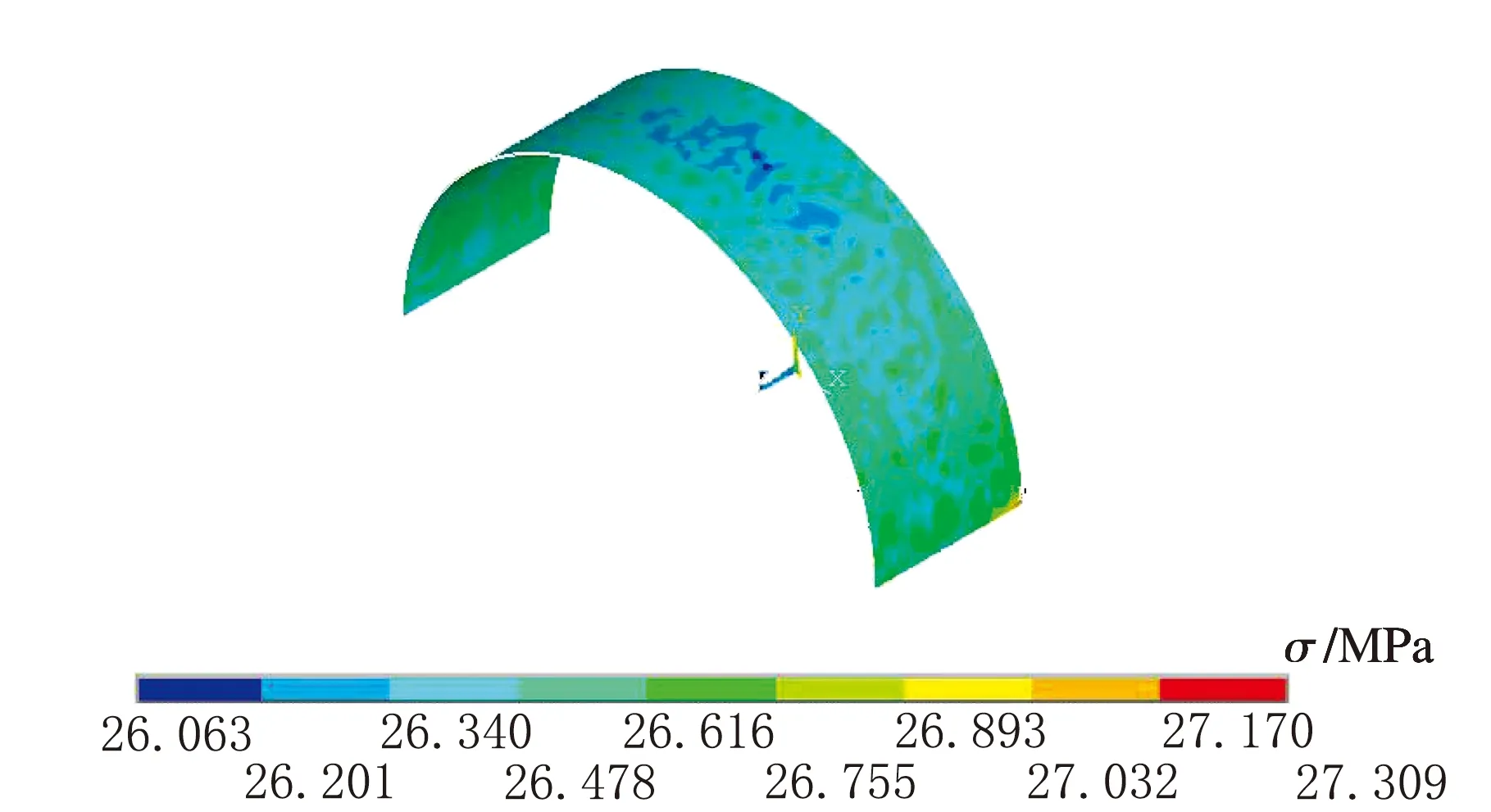
圖3 不含凹坑儲存容器分析結果

由圖3可知，容器壁面上應力分布較為均勻，容器筒體的等效應力最大為27.3 MPa，由于該應力遠小于材料的許用應力102.5 MPa，說明在沒有缺陷時，容器本身能夠滿足強度的安全性要求，該容器在出廠時無強度安全問題。

3.2 含凹坑缺陷儲存容器有限元分析

儲存容器存在凹坑缺陷會影響其應力分布的均勻性，造成應力集中，應力在缺陷位置會出現急劇增大現象，給容器的使用帶來安全隱患[10]。通過建立具有球形凹坑缺陷的容器模型，進行力學分析，確定應力集中位置及最大等效應力，研究凹坑缺陷直徑和深度2個參數對容器應力集中的影響程度，分析了其隨直徑和深度的變化趨勢，為后續的安全評定工作提供依據。

3.2.1 不同直徑下等效應力分析

假設凹坑缺陷深度h=50 mm固定不變時，當凹坑缺陷直徑D=400、500、600、700、800及900 mm時，對模型進行等效應力計算，應力云圖見圖4，最大等效應力隨凹坑缺陷直徑的變化趨勢見圖5。

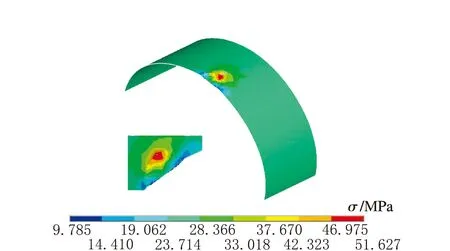
a D=400 mm

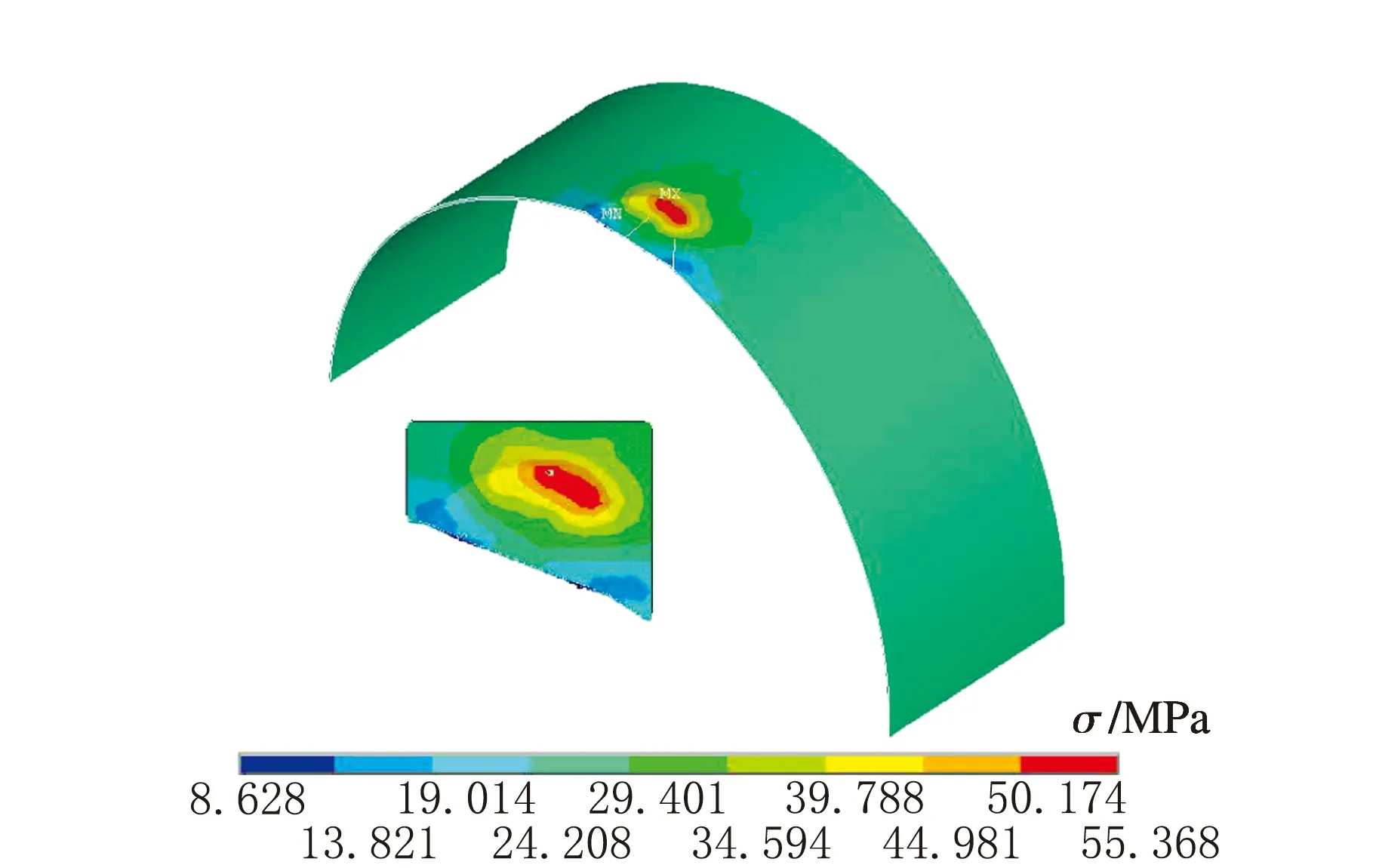
b D=500 mm

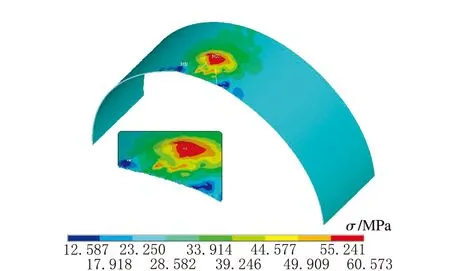
c D=600 mm

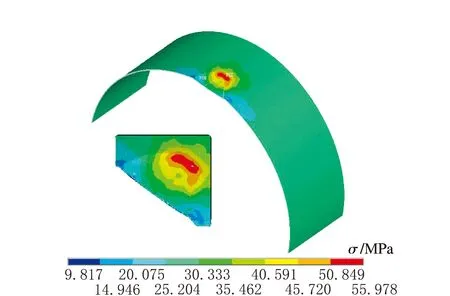
d D=700 mm

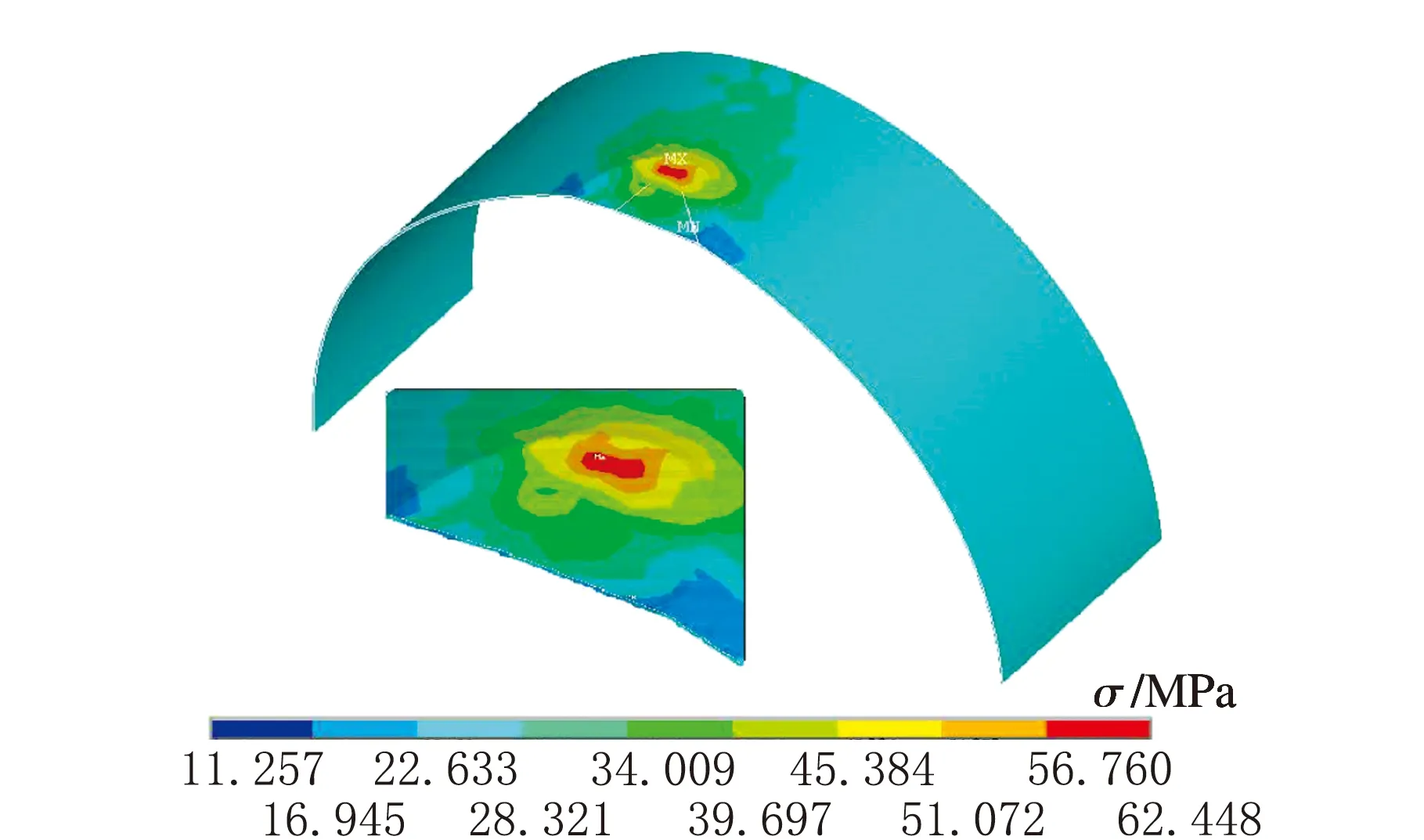
e D=800 mm

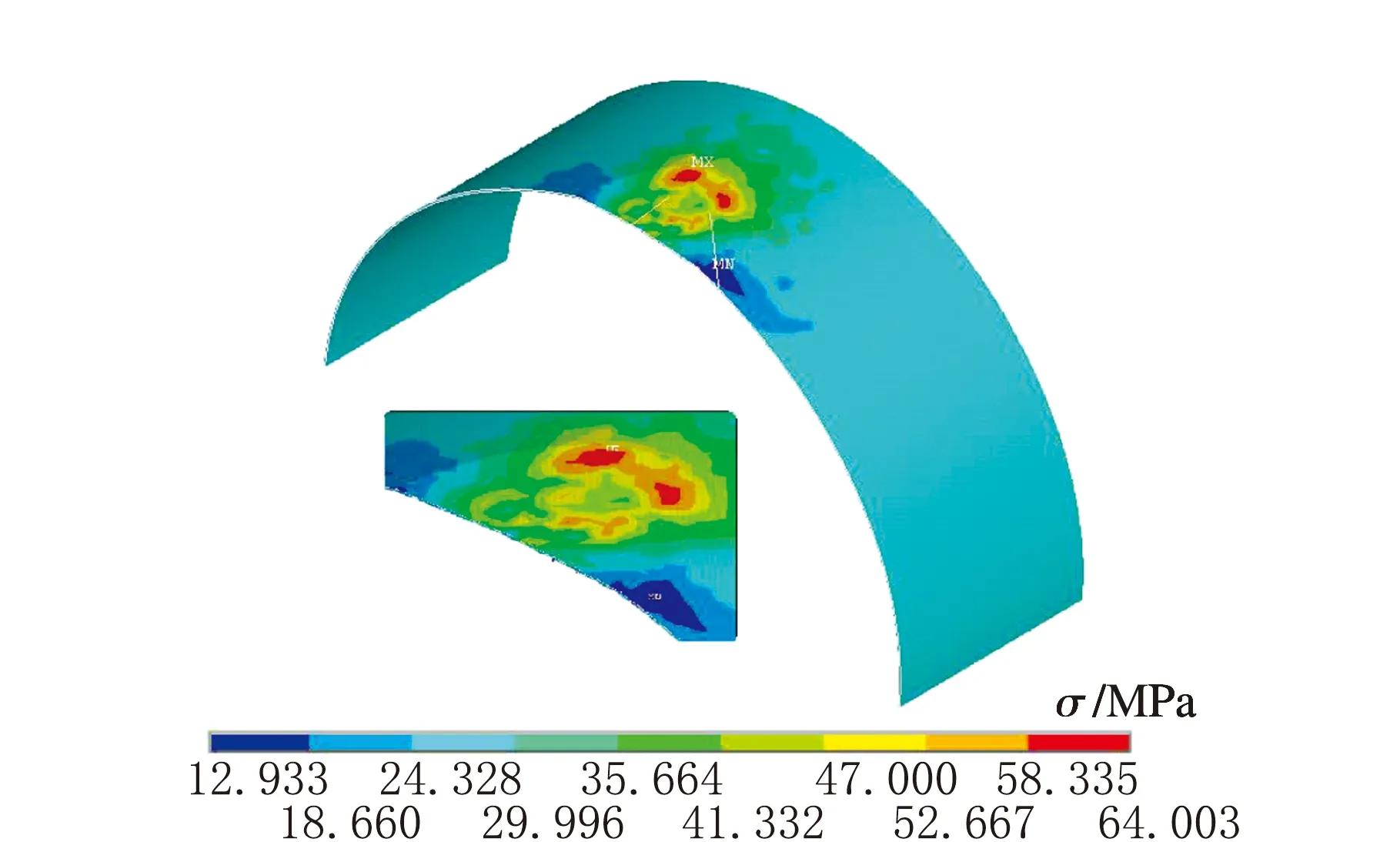
f D=900 mm圖4 不同直徑下應力云圖

由圖4可知，最大等效應力均出現在容器外壁凹坑頂點處，最大應力值均大于不含凹坑容器壁面的等效應力，說明在凹坑缺陷部位出現了應力集中現象。

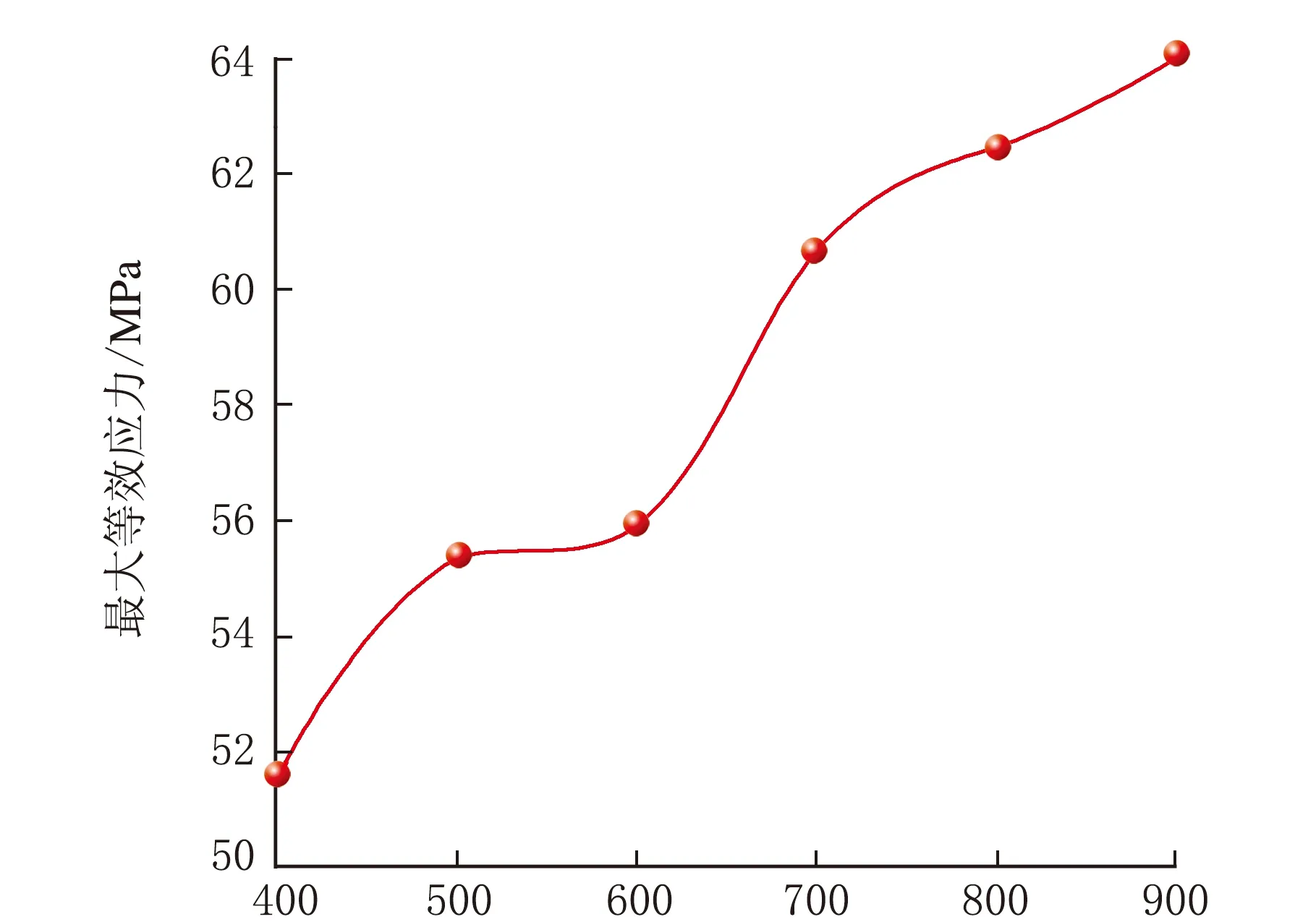
D/mm圖5 最大等效應力隨凹坑缺陷直徑的變化趨勢圖

由圖5可知，最大等效應力隨著凹坑缺陷直徑的增加而增大，該值基本與凹坑缺陷直徑成正比關系。當凹坑缺陷直徑從500 mm增加到600 mm時，等效應力值基本無變化，可能是由于在該條件下，凹坑缺陷深度對等效應力起到限制作用。

3.2.2 不同深度下等效應力分析

假設凹坑缺陷直徑固定不變為D=600 mm，分別分析凹坑缺陷深度h=50、60、70、80、90、100及110 mm時的受力情況，由于h=50 mm、D=600 mm已經分析過，故只需要對h=60～110 mm分析即可，結果見圖6。

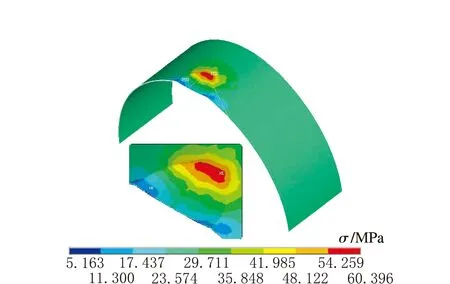
a h=60 mm

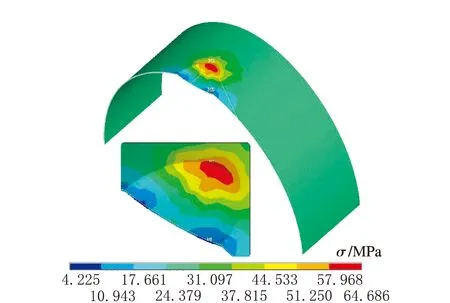
b h=70 mm

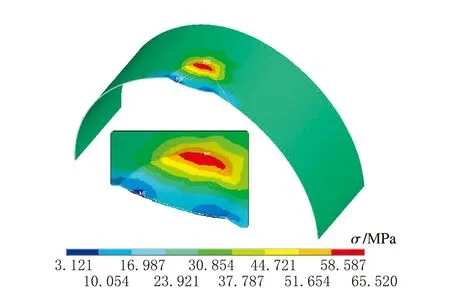
c h=80 mm

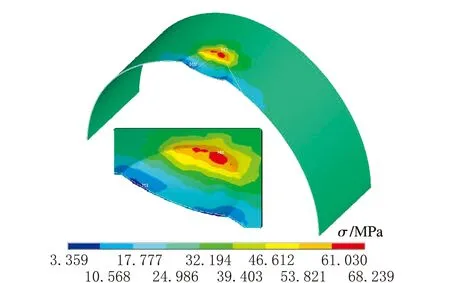
d h=90 mm

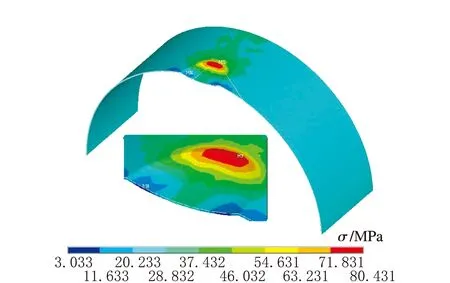
f h=110 mm圖6 不同深度下應力云圖

由圖6可知，隨著凹坑缺陷深度的增加，最大等效應力逐漸增大，當凹坑缺陷深度為110 mm時，等效應力可達到80.4 MPa，接近材料的許用應力。

容器等效應力隨凹坑缺陷深度變化趨勢見圖7。

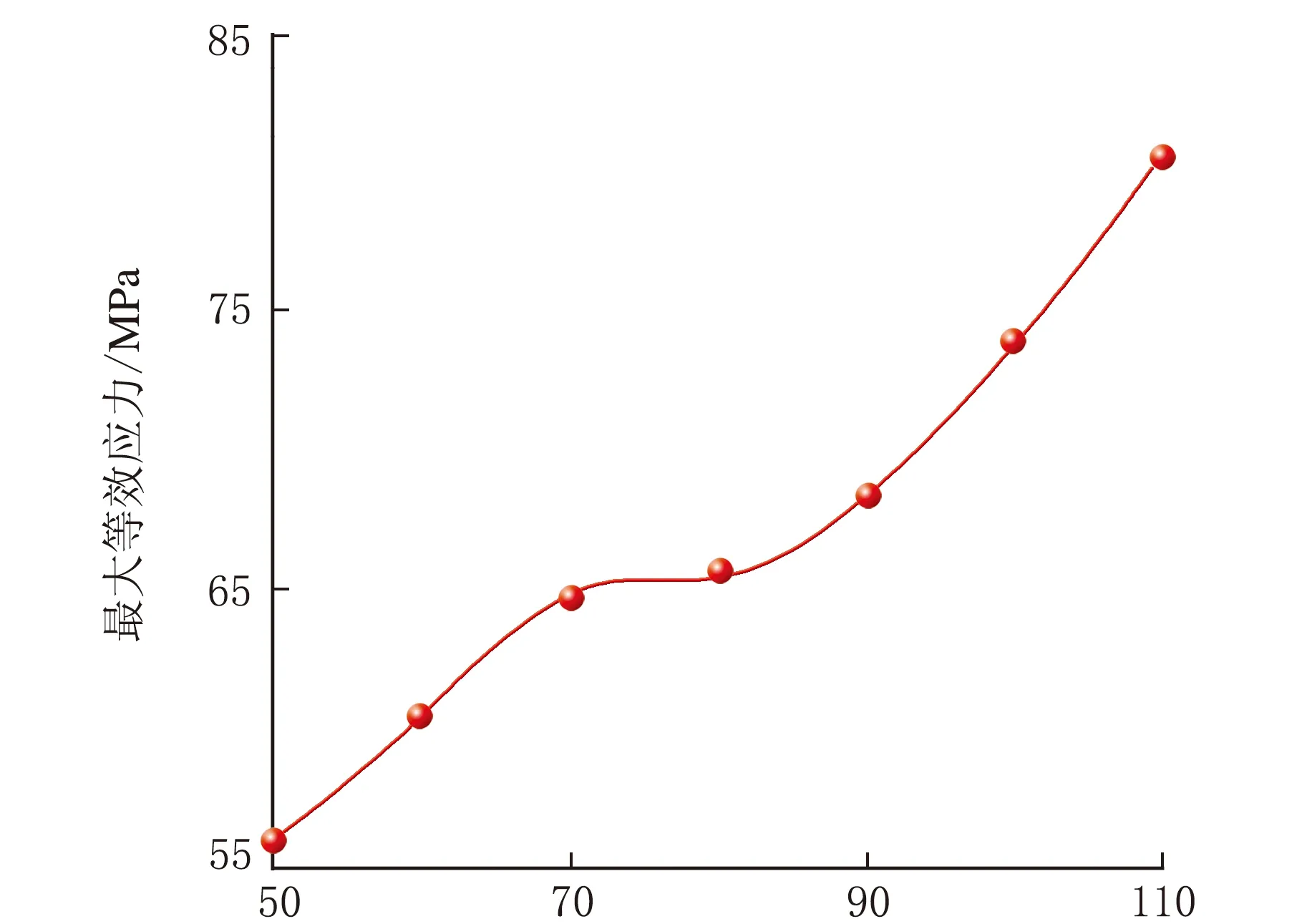
h/mm圖7 最大等效應力隨凹坑缺陷深度的變化趨勢

由圖7可知，最大等效應力與凹坑缺陷成正比關系，且變化趨勢較為明顯，當凹坑缺陷深度從70 mm增加到80 mm時，等效應力基本不發生變化。在該條件下，該位置處可能發生了塑性變形，材料出現硬化強化作用，承載能力會進一步增強[11-12]。

通過對比圖5與圖7可知，最大等效應力隨凹坑缺陷深度增加變化較快，凹坑缺陷深度從50 mm增加到110 mm，最大應力從55 MPa增長到80 MPa，而隨凹坑缺陷直徑變化較為平緩，因此凹坑缺陷深度對最大等效應力的影響大于凹坑缺陷直徑的影響。同等條件下，凹坑缺陷深度的改變容易引起容器局部產生更大的集中應力，對容器的安全性和可靠性影響更大。

3.3 補強措施及補強效果

由上述分析可得，當容器表面不含凹坑時，容器所受應力均勻分布，均值約為26.5 MPa(見圖3)；當容器表面含有凹坑(D=600 mm，h=50 mm)時，在凹坑附近形成應力集中，最大應力為σ=55.24 MPa(見圖4c)。該等效應力值遠小于容器材料的許用應力[σ]=102.5 MPa，可以保證容器的安全性。由于容器儲存介質的特殊性，推進劑加注事關國家安全問題，應杜絕容器存在的一切不安全因素。因此，對凹坑部位進行補強，補強鋼板與容器本體材料一致為0Cr18Ni9Ti，補強鋼板尺寸為100 mm×100 mm，厚度δ=10 mm，對該補強后模型進行受力分析后，應力云圖見圖8，位移云圖見圖9。

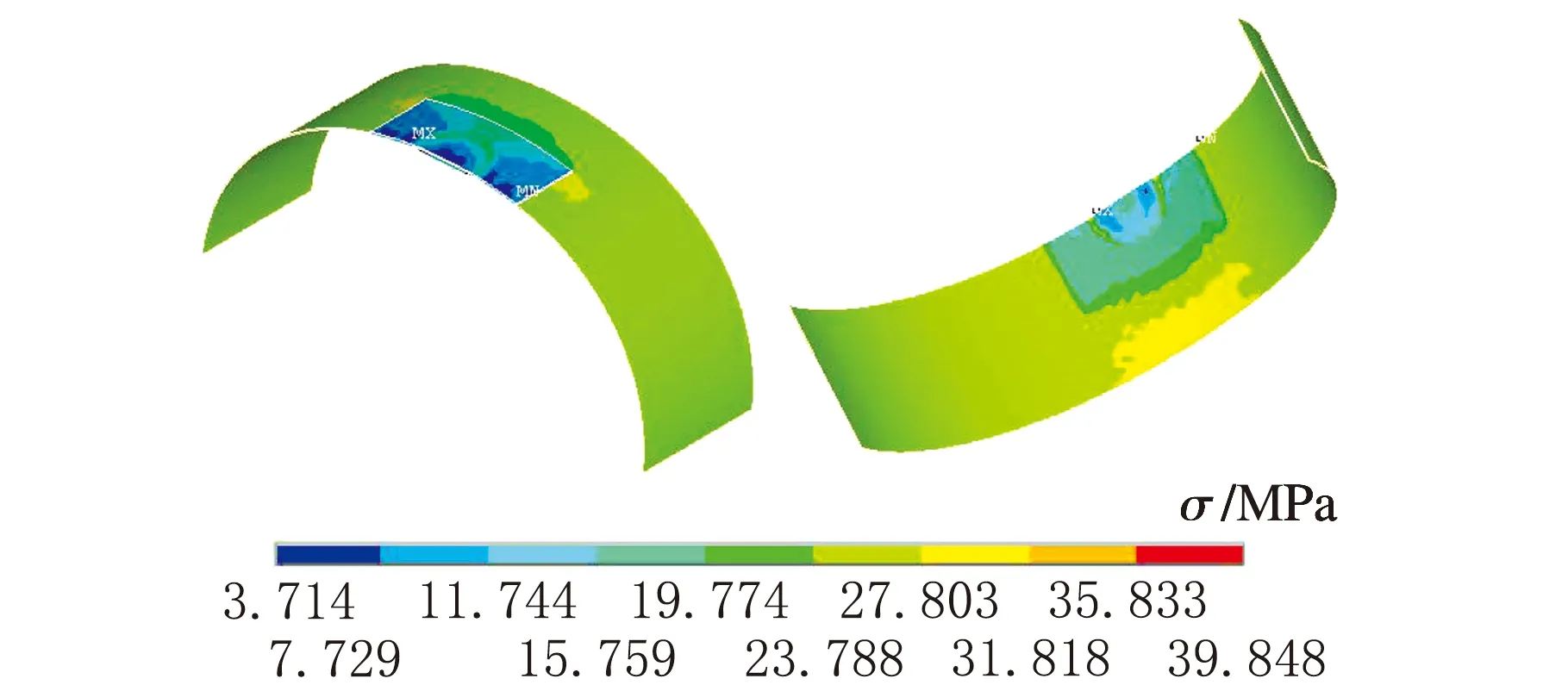
圖8 補強后應力云圖

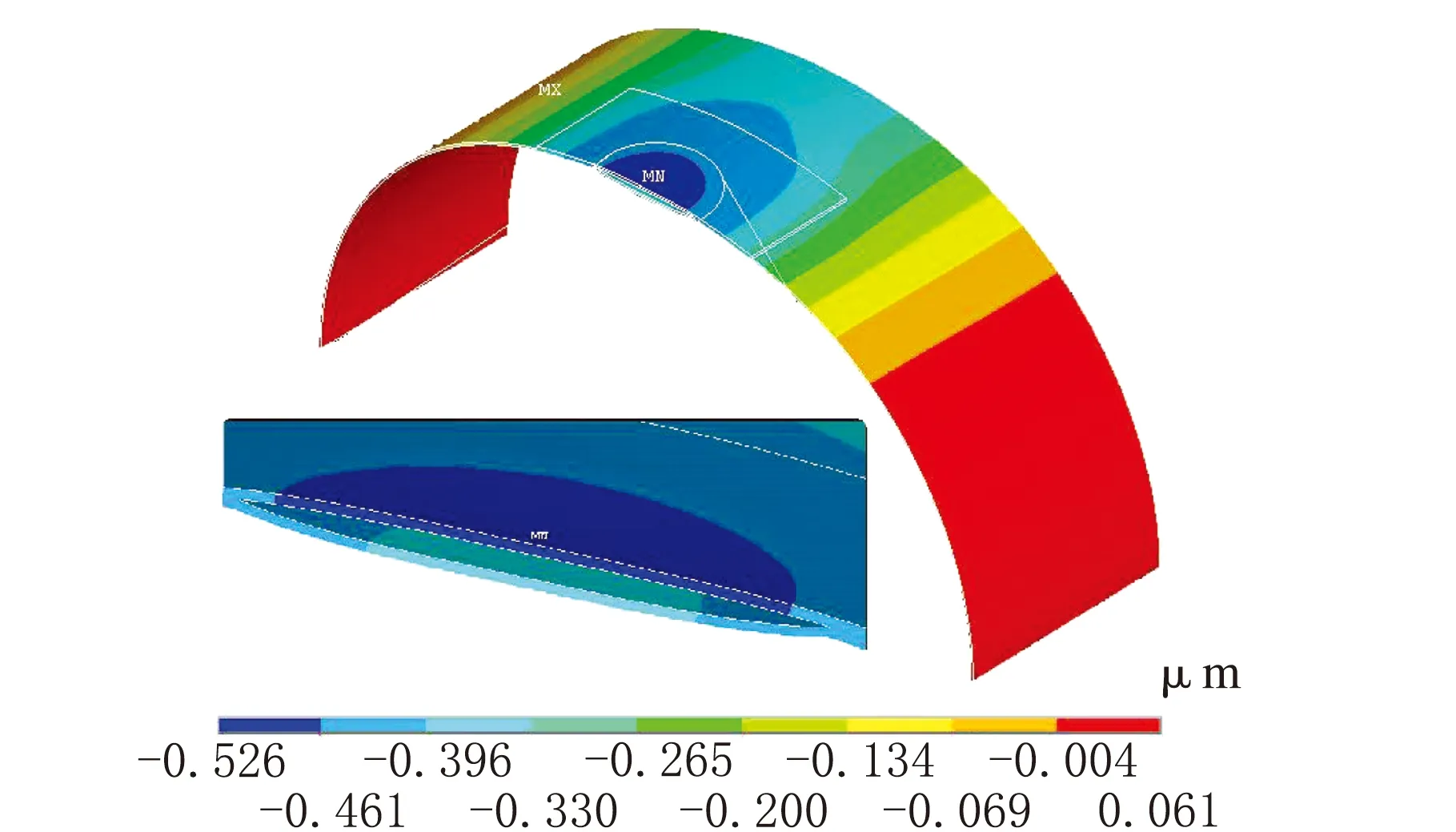
圖9 補強后位移云圖

由圖9可知，補強板與凹坑形成的空間，當承受壓力時該空間較安裝后縮小，壓縮內部空氣，容易產生正壓，因此在補強板上設有開孔及角閥，以便在容器增壓過程中對該空間放氣。

凹坑補強前后應力云圖對比見圖10。

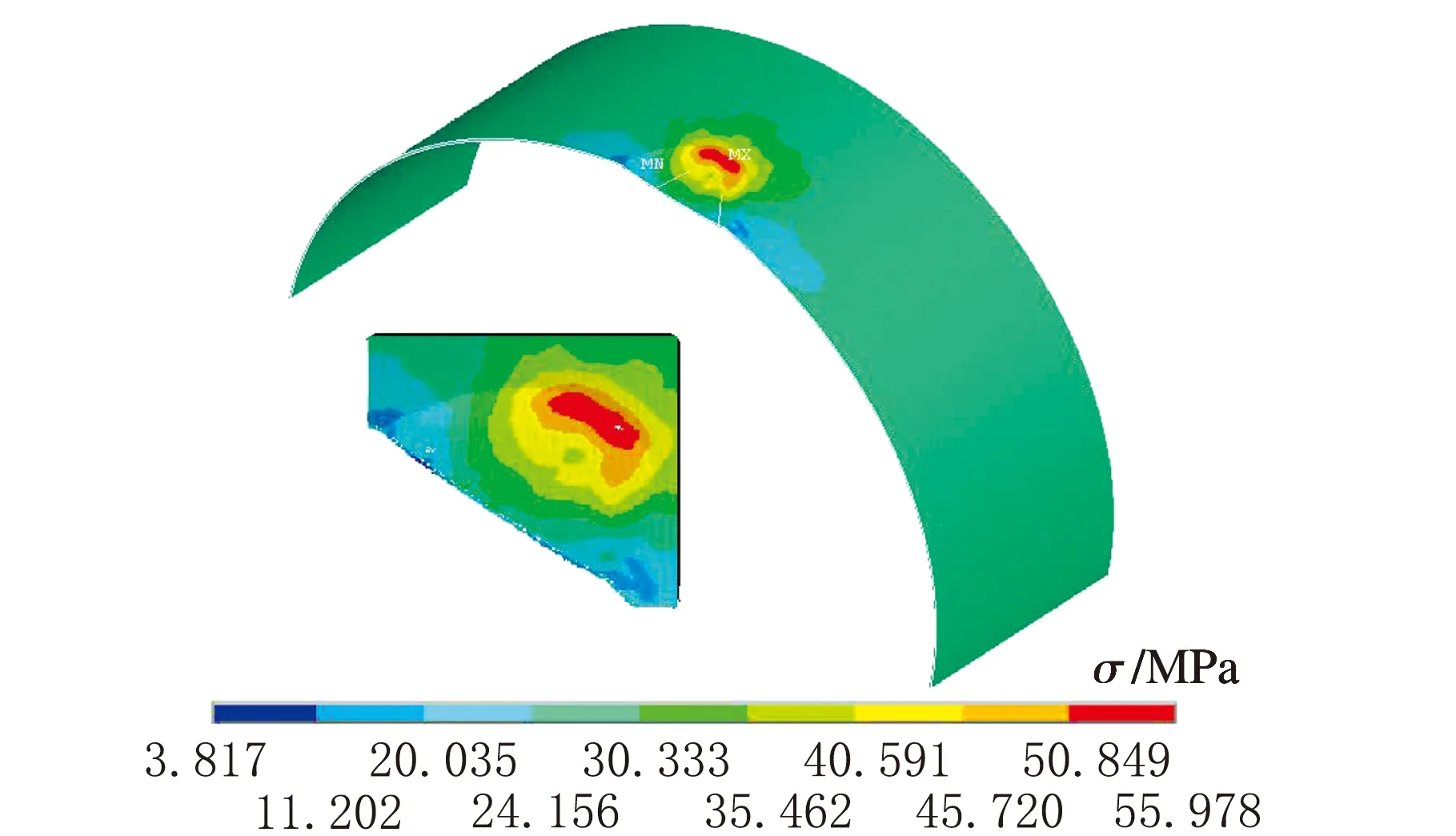
a 補強前

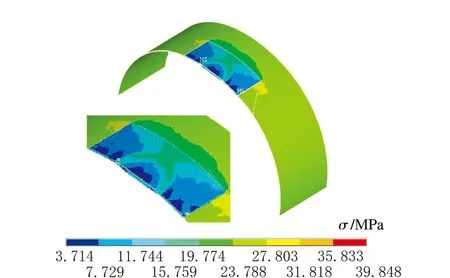
b 補強后圖10 凹坑補強前后應力云圖對比

由圖10可知，通過對比補強前后等效應力云圖，發現經補強后補強區域內筒體的等效應力明顯降低，普遍低于容器本體應力值，最大集中應力也由補強前的55.9 MPa降低至39.8 MPa，有效改善了凹坑附近的應力集中現象，容器的可靠性、安全性顯著提升。

4 結 論

(1)推進劑儲存容器凹坑缺陷會引起應力集中現象，最大等效應力點均位于容器外壁凹坑頂點處；

(2)當推進劑儲存容器存在凹坑，凹坑缺陷深度對最大等效應力的影響程度要大于凹坑缺陷直徑，是影響儲存容器安全性的關鍵因素，需在實際中多關注缺陷的深度，深度增加到一定程度，應停止使用；

(3)采取補強措施可以有效降低凹坑附近的應力集中現象，可降低容器使用風險，兼具安全性和經濟性，但在實際中，由于儲存介質的特殊性，一旦出現缺陷，應密切關注或更換。