基于三元組排序局部性的SOCFS改進算法

吳昌明,趙興濤,柳可鑫

(中國人民公安大學 信息技術與網絡安全學院,北京 102623)

0 概述

在大數據時代背景下,數據維度急劇增長,大量的高維特征廣泛存在于模式識別、機器學習、生物信息等領域,如何在高維數據下準確地獲取對學習任務有利的信息已成為當前研究的熱點。在實際應用中,多數特征是與當前學習任務無關的冗余特征或者噪聲特征,這些冗余和噪聲特征會給學習任務帶來很多不利影響,比如過擬合、低效率。因此,降維成為處理高維數據的重要技術[1]。特征選擇[2-3]是當前廣泛使用的降維方法[4-5],其在高維數據中選出與當前學習任務相關的特征,去除與當前學習任務無關的冗余和噪聲特征,從而降低數據空間維度,便于后續數據處理與任務分析。

在實際應用中,通常需要解決缺少數據標簽信息的非監督[6-7]特征選擇問題[8-9]。由于數據樣本的標簽信息未知,因此需要進行聚類,挖掘無標簽數據的潛在規律和性質并劃分簇結構,從而找到對應的類別。基于不同的特征選擇判據以及不同的聯合框架,研究者們提出了大量面向聚類應用的特征選擇算法,比如拉普拉斯的特征得分法(LS)[10]、非負譜分解的判決性特征選擇法(NDFS)[11]、同時正交基聚類特征選擇法(Simultaneous Orthogonal Basis Clustering Feature Selection,SOCFS)[12]等。然而,現有的非監督特征選擇方法雖然在實際應用中具有良好表現,但是在聚類性能上還有較大的提升空間。因此,本文面向聚類應用研究非監督特征選擇問題,選取與當前學習任務相關且具有局部結構保持性與判別性的特征,并去除冗余和噪聲特征,以提升聚類性能。

1 相關工作

近年來,非監督特征選擇成為人工智能的研究趨勢。早期面向聚類應用的特征選擇算法基于某種特定的判據,單獨評估每一個特征的重要性,從而選擇在此判據下的最優特征。此類方法的代表有最大方差法[13]、LS法[14],其中LS法選擇對應最大拉普拉斯得分的特征,而相應的拉普拉斯得分可以用來反映局部流形結構的保持能力。然而,單獨評估每一個特征重要性的方法不能用于處理多類簇結構。也就是說,對于多類簇問題,很可能不同特征對不同類簇具有不同的判別能力,而單獨評估每一個特征的方法忽略了特征之間的組合對類簇的判別作用。因此,文獻[15]提出一種面向多類簇應用的非監督特征選擇算法(MCFS),其運用譜回歸的兩步法并聯合l1范數最小化進行特征選擇。

受聯合求解的啟發,現有的非監督特征選擇算法大多采用一個特定的聯合框架來選擇最合適的特征子集。NDFS是在一個聯合框架中,同時進行非負譜分析和l2,1范數正則化回歸,從而實現在整個特征集合中批量選擇最具判別性的特征子集。無監督的規范化判別特征選擇算法(UDFS)[16]綜合了分析和最小化范數以確定特征。然而,UDFS和NDFS算法忽略了噪聲和異常值的影響,魯棒性較差。因此,文獻[17]提出一種魯棒非監督特征選擇算法(RUFS),其通過局部學習正則化非負矩陣分解來學習偽標簽,同時聯合l2,1范數正則化回歸進行特征選擇,從而有效處理異常值和噪聲。SOCFS[12]利用雙正交半非負矩陣分解進行正交基聚類,捕捉潛在的類簇中心,從而進一步指導特征選擇過程。

上述特征選擇方法已經在實際應用中取得了較好的應用效果,但在聚類性能方面依然有較大的提升空間。由于已有特征選擇方法忽略了排序局部性對特征選擇過程的影響,即特征選擇后并不能保持數據點原始的近鄰排列順序,而排序局部性卻對基于距離的聚類任務影響較大,因此本文利用數據的三元組局部結構,構建數據之間的排序關系并對該關系在特征選擇過程中進行局部保持,提出基于三元組排序局部性的SOCFS改進算法,從而選擇排序局部性保持較好的特征,應用于后續的非監督學習任務。

2 SOCFS改進算法

2.1 SOCFS算法

SOCFS是一種非監督特征選擇算法。為對無標簽數據進行有效的特征選擇,該算法設計了一個含有新型目標矩陣的正則化回歸公式。目標矩陣通過正交基聚類來捕獲映射后的數據點潛在的類簇中心,繼而指導映射矩陣選擇判別性的特征。SOCFS未使用數據點的局部結構信息作為目標函數的附加項,而是在提出的目標函數中通過使用具有統一項的目標矩陣指導正交基聚類,直接計算潛在的類簇信息,并且可采用一個簡單的優化算法實現目標函數最小化。在多個數據集上的實驗結果表明:與現有特征選擇算法相比,SOCFS獲得了更加有效的聚類結果。

(1)

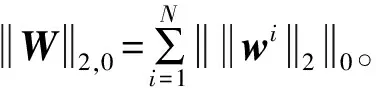
λ>0

(2)

約束的意義為:1)B的正交約束使B的每一列都是獨立的;2)E的正交和非負約束使E的每一行都只有一個非零元素。由此可以看出,B作為基矩陣,有正交性,E作為編碼矩陣,ET中每一列的非零元素選擇B中的一列。該約束確保了SOCFS算法基于距離的正交基聚類。

T=BET使用正交基B和編碼矩陣E對映射后的數據點WTX進行聚類,所以T能估計WTX的潛在類簇中心。然后,X經過W的映射后,可以成功逼近由T估計出的潛在類簇中心。由于B的正交約束使得WTX映射后的類簇更加分散(類簇中心相互獨立),因此使得W能選擇更有判別性的特征。對于E,已有方法通過近似正交約束的方式解決問題式(2)。然而,因為該方法是基于非負矩陣分解,在多數情況下其處理的是非負約束而不是正交約束,且也不能完全保證E是一個正交矩陣,所以E不能作為編碼矩陣。因此,SOCFS算法的目標函數為:

s.t.BTB=I,ETE=I,F=E,F≥0

(3)

其中,F是一個輔助變量,并帶有一個附加約束F=E,這一步轉換的目的是從E中分離出非負約束并將該約束施加到新變量F上。當E保持正交性時,F可以通過約束F=E保證E的非負性。改寫問題式(3),得到最終SOCFS算法的目標函數為:

s.t.BTB=I,ETE=I,F≥0

(4)

其中γ>0是一個控制F和E相等程度的參數。

2.2 排序局部性

如圖1所示,假設在原始空間(見圖1(a))中,數據點x0有4個近鄰x1、x2、x3、x4,其中相同顏色表示同一類別,即(x0,x1,x2)屬于類別1,x3屬于類別2,x4屬于類別3,線段長短表示距離遠近,距離排序為1→2→3→4。當采用W矩陣映射進行特征選擇時,可以看到圖1(b)中未經過排序局部性保持的特征在投影之后,排序局部性發生了變化,距離排序變為3→4→1→2,這說明原始空間中數據的拓撲結構發生了變化,在基于距離的聚類中,后續過程將會把中間部分的y0、y4、y2聚為一類,從而導致聚類結果的不準確。本文將經過特征選擇矩陣投影到新的空間后,使數據的排序得到保持,也就是保持數據的局部結構,從而得到正確的聚類結果,即y0、y1、y2聚為一類,y4為一類,y3為一類,如圖1(c)所示。綜上所述,在基于聚類的任務中,近鄰之間的相對遠近關系也稱為排序局部性[18-19],對于特征選擇過程極其重要。

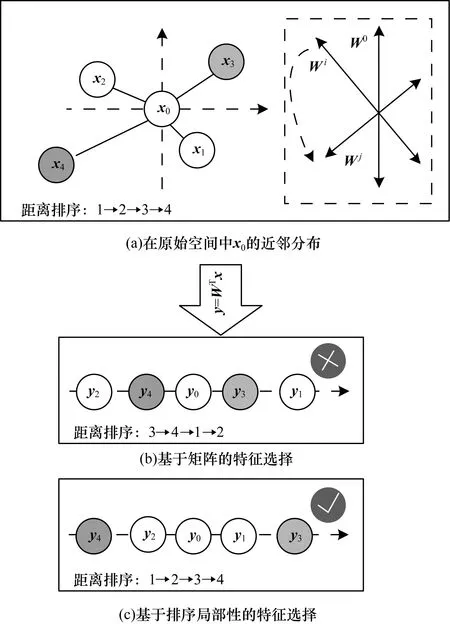
圖1 排序局部性原理

2.3 三元組排序局部性

對數據點xi,經過特征選擇矩陣W的映射后得到所選擇的新特征組,記作yi=WTxi,因此有Y=WTX。

基于三元組引導的排序局部性表示若存在一個數據點xi及其近鄰組成一個三元組向量(xi,xp,xq),經過特征選擇矩陣W的映射后,得到一個新特征組構成的三元組(yi,yp,yq)。如果當dist(xi,xp)≤dist(xi,xq)成立時,則有dist(yi,yp)≤dist(yi,yq)。因此,筆者認為排序局部性,也就是近鄰的遠近關系在基于聚類的任務中得到了保持。

(5)

(6)

基于以上數學推導,最終得到保持排序局部性的損失函數為:

(7)

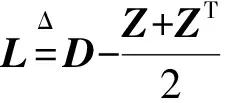
綜上,本文得到基于三元組引導排序局部性的損失函數。

2.4 TOL-SOCFS算法

在原有SOCFS算法的基礎上,本文加入三元組引導保持排序局部性的附加項Tr(WTXLXTW),得到最終改進算法的目標函數為:

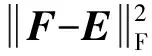
s.t.BTB=I,ETE=I,F≥0

(8)

其中,α是一個標量常數,控制保持排序局部性的損失函數項的相對重要性。

采用交替迭代的方式對式(8)進行優化,并得到基于三元組引導排序局部性的SOCFS改進算法(TOL-SOCFS)。

1)W更新:固定B、E、F求使目標函數值最小的W,與W相關的子問題如下:

(9)

令J(W,B,E,F)對W的導數等于0,有:

α(XLXT+XLTXT)W=0?

W=(XXT+λD+0.5αX(L+LT)XT)-1XEBT?

W=(XXT+λD+αXLXT)-1XEBT

(10)

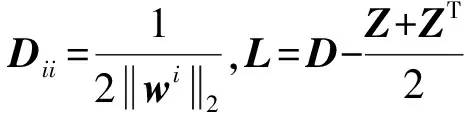
2)B更新:固定W、F求使目標函數值最小的B,與B相關的子問題如下:

(11)

(12)

解析解為:

(13)

(14)

其中,UB和VB分別為矩陣ETXTW奇異值分解后的左右特征向量。

3)E、F更新:固定B和W求使目標函數值最小的E和F,E和F通過固定一個并更新另一個的方式交替迭代。與E相關的子問題如下:

s.t.ETE=I

(15)

子問題可重寫為:

XTWWTX)+γTr(ETE-2ETF+FTF)=

(16)

(17)

其中,UE和VE分別為矩陣BTWTX+γFT奇異值分解所得的左右特征向量。

與F相關的子問題可以寫為:

(18)

子問題式(18)的解可以改寫為:

(19)

算法1為E和F的更新算法,整體優化算法見算法2。由更新規則式(10)、式(14)、式(17)和式(19)可知,目標函數單調下降。

算法1E和F更新算法

輸入矩陣Ft、Wt、Bt,參數γ

輸出Et+1=E′s、Ft+1=F′s

初始化s=0、F′s=Ft

1.Repeat Step 2～Step 4;

4.s=s+1;

算法2TOL-SOCFS算法

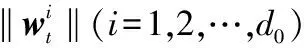
初始化t=0、Dt=I、Bt和Et

1.Construct k-neighbor graph,obtaining Laplacian matrix L;

2.Repeat Step 3～Step 7;

3.Update Et+1and Ft+1by algorithm 1;

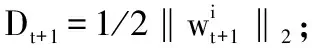
7.‖ΔJ(Wt,Bt,Et,Ft)‖≤ε;

2.5 TOL-SOCFS算法復雜度分析

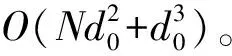
3 實驗結果與分析

3.1 實驗設置

實驗在6個公開數據集上進行K均值聚類[19-21]:目標圖像數據集(COIL20),字母讀音識別數據集(Isolet1),手寫數字數據集(USPS),人臉圖像數據集(YaleB、UMIST、ORL)。在每個數據集上,本文提出的TOL-SOCFS算法都與下列5種非監督特征選擇算法以及原SOCFS算法進行比較,并且未經過特征選擇處理的所有特征被作為對比評估標準[22-23]。

1)無監督的規范化判別特征選擇算法(UDFS):基于局部判決得分進行特征選擇,其中局部判決得分基于l2,1正則化矩陣反映局部結構信息。

2)面向多類簇應用的非監督特征選擇算法(MCFS):基于l1正則化矩陣的譜回歸兩步法選擇特征。

3)非負譜分解的判決性特征選擇算法(NDFS):基于非負的譜分析和l2,1正則化回歸的聯合框架選擇特征。

4)魯棒非監督特征選擇算法(RUFS):基于l2,1范數且帶有局部學習的非負矩陣分解和l2,1正則化回歸的聯合框架選擇特征。

5)拉普拉斯的特征得分法(LS):先根據算法計算拉普拉斯得分,再選擇得分最高的特征,其中計算得到的拉普拉斯得分可以反映特征的局部保持能力。

本文使用聚類精確度(ACC)和歸一化互信息(NMI)評估不同算法選擇的特征集的聚類結果[24]。對于LS、MCFS、UDFS,NDFS和RUFS,設置近鄰參數k的值為5。因為SOCFS和TOL-SOCFS將數據點的局部結構信息嵌入到三元組的損失函數構建中,所以不需要額外設置任何的近鄰參數,其中將映射空間的維數m設為潛在類簇的數量c。

針對TOL-SOCFS算法,本文同樣采用網格搜索策略在{10-6,10-4,…,104,106}范圍內調整所有參數,不同的是相比其他非監督特征選擇算法,TOL-SOCFS算法需要調整更多的參數。對于前5個數據集,設置選擇的特征數目為{50,100,…,300}。對于USPS數據集,考慮其特征維數的限制,設置選擇的特征數目為{50,80,…,200}。本文對所有實驗都重復了20次,每次實驗均隨機初始化并列出ACC和NMI的平均值和標準差,同時隨機初始化NDFS、RUFS、SOCFS等算法的變量。

3.2 結果分析

TOL-SOCFS算法與其他非監督特征選擇算法的ACC和NMI的平均值和標準差對比結果見表1和表2,其中最優結果加粗表示,括號內的值為當前結果下對應最合適選取特征的數目。由表1和表2可以看出,TOL-SOCFS算法在6個數據庫上都產生了比其他非監督特征選擇算法更好的實驗結果,并且在所選特征數目較少時,TOL-SOCFS算法也有較好的聚類性能。

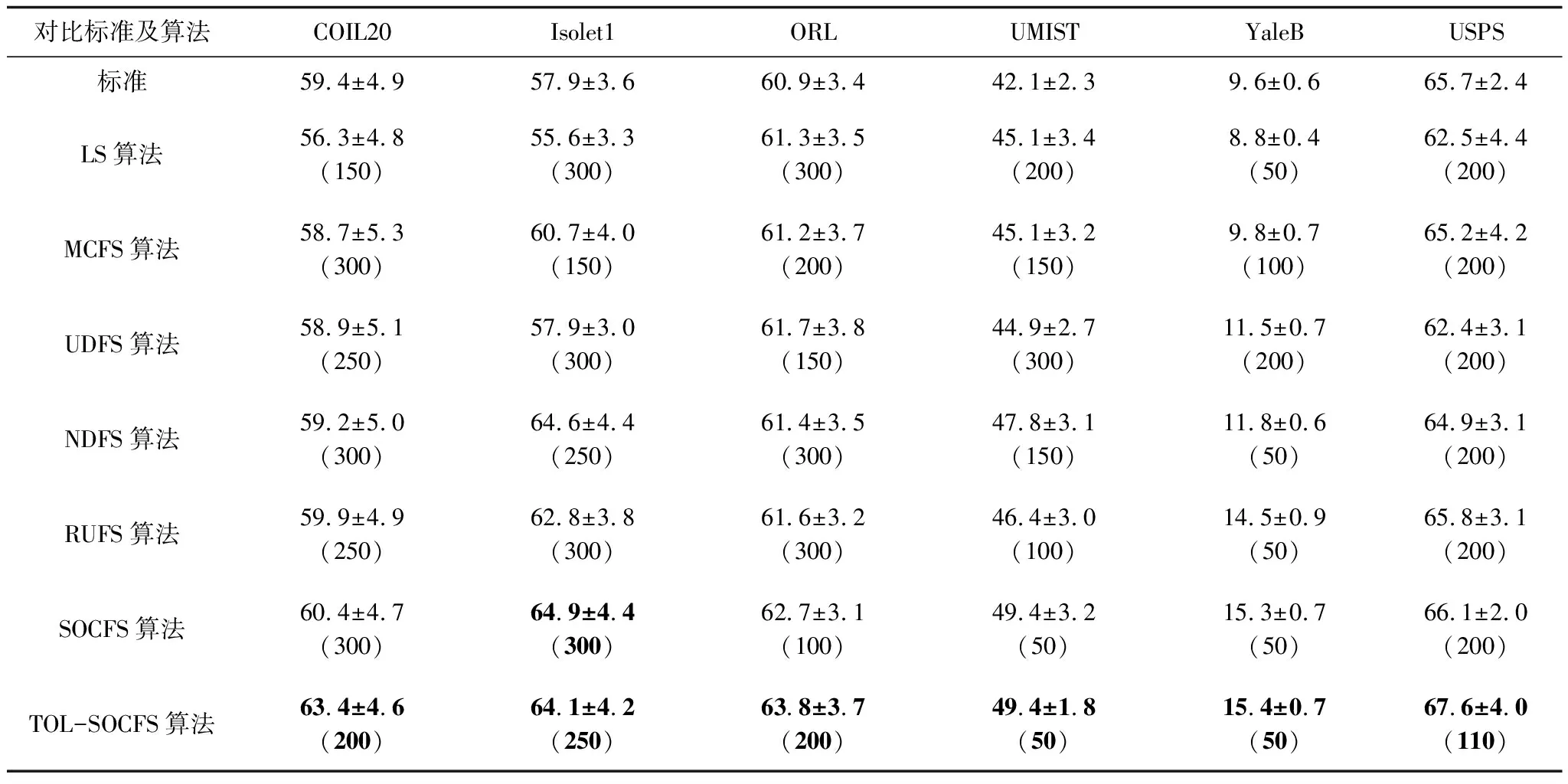
表1 TOL-SOCFS算法與其他非監督特征選擇算法的ACC對比結果

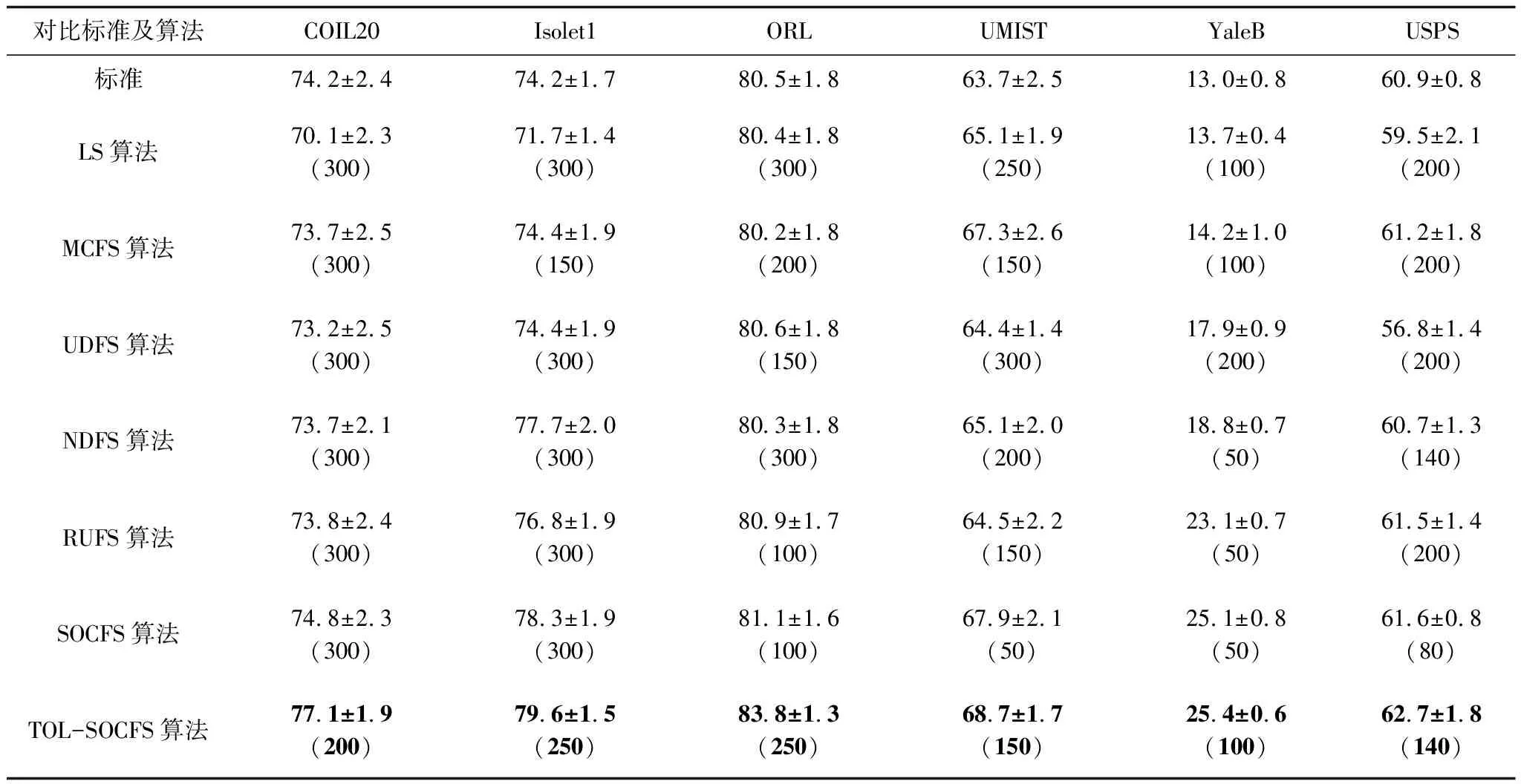
表2 TOL-SOCFS算法與其他非監督特征選擇算法的NMI對比結果

如表1所示，在COIL20數據集上，本文提出的TOL-SOCFS算法具有接近3%的聚類性能提升，表明了TOL-SOCFS算法的ACC聚類精確度較高。可以看出，在COIL20數據集上，TOL-SOCFS算法可以選擇更少的特征(即200維)，但得到比SOCFS算法300維特征更好的結果，驗證了TOL-SOCFS算法特征選擇的有效性。此外，在USPS數據集上，TOL-SOCFS算法在110維特征數的情況下，可以得到比200維特征的SOCFS算法更好的聚類結果，驗證了TOL-SOCFS算法的有效性。同樣地，在互信息NMI的度量指標上，如表2所示，TOL-SOCFS算法取得了所有算法中最好的互信息結果，并且在COIL20數據集上，僅通過200維特征即可獲得比其他算法300維特征更好的聚類性能，進一步驗證了TOL-SOCFS算法的有效性。以上結果主要得益于三元組引導的排序局部性對原始數據拓撲結構的保持，即原始數據中近鄰的相對遠近關系與數據原始幾何結構得到保持，有利于選擇具有局部結構保持性及判別區分度高的特征。因此，實驗證實TOL-SOCFS算法的聚類性能優于現有非監督特征選擇算法。

3.3 算法收斂性分析

TOL-SOCFS算法的收斂性曲線見圖2。在6個數據集上的實驗結果表明,TOL-SOCFS算法可以在60次迭代內實現收斂,表明其具備快速收斂能力。

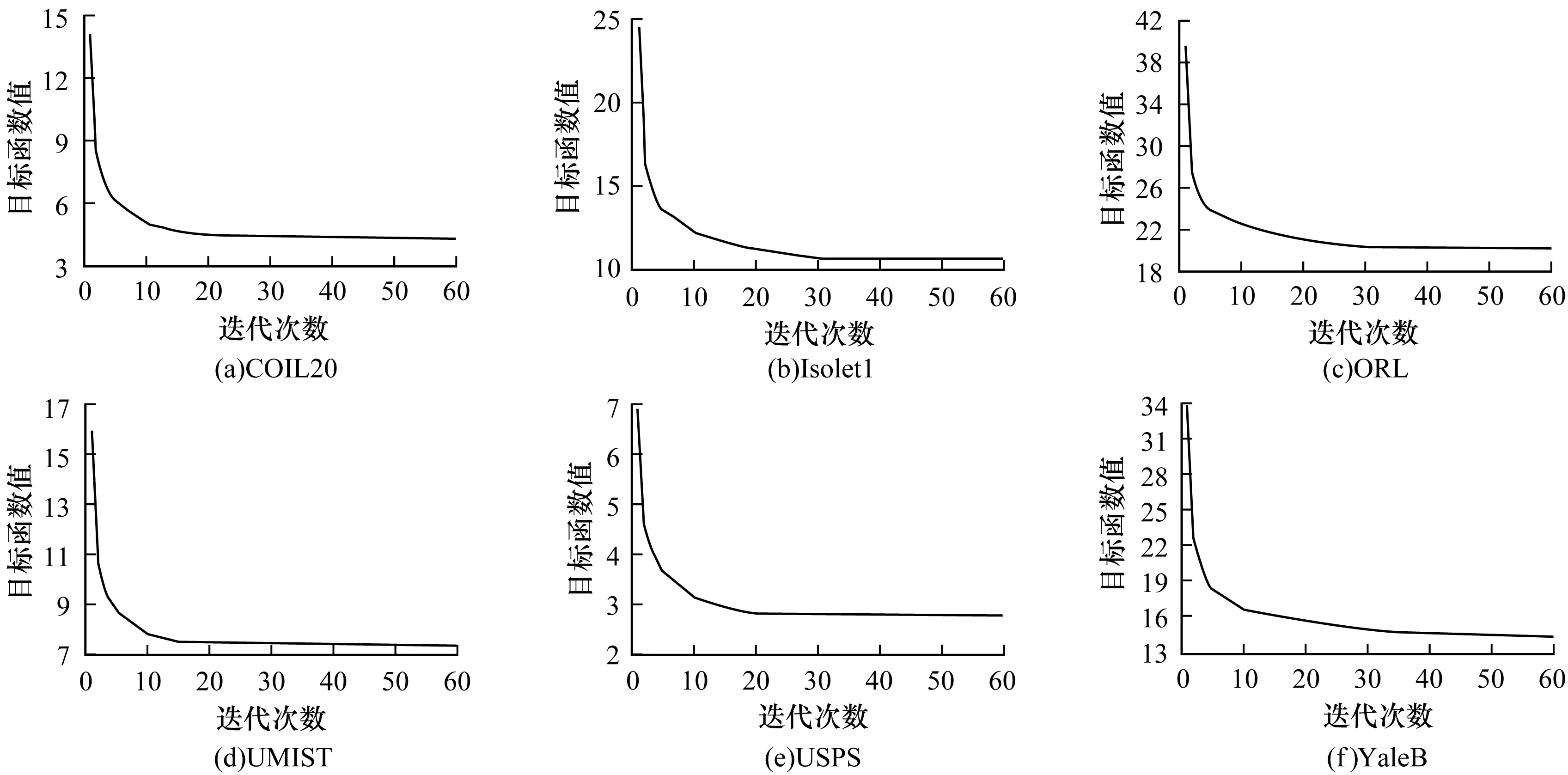
圖2 TOL-SOCFS算法的收斂性曲線

4 結束語

本文提出一種基于三元組排序局部性的SOCFS改進算法(TOL-SOCFS),利用數據的三元組局部結構,構建數據之間的排序關系并對該關系在特征選擇過程中進行局部性保持,從而選擇排序局部性保持較好的特征,用于后續的非監督聚類任務。在6個公開數據集上的聚類實驗結果表明,TOL-SOCFS算法具有比其他非監督特征選擇算法更好的聚類性能,驗證了其有效性。鑒于TOL-SOCFS算法利用三元組排序局部性在樣本維度上保持映射前后的一致性能力,下一步將更多關注三元組排序局部性在特征維度上的映射保持關系,通過保持映射前后特征的相似性,進一步提升非監督特征選擇算法的整體性能。