基于測井數據的砂巖型鈾礦異常識別BP神經網絡方法應用

康乾坤，路來君，尚殷民

(吉林大學地球科學學院,長春 130061)

在礦產勘查中，測井數據屬于分辨率最高的一種地學屬性信息，是能直觀反映出縱深方向上地球物理性質變化的屬性。因而具有很高的研究和工程價值。通過對鈾礦測井數據的分析可以推斷出鈾礦異常的產生位置，從而對鈾礦勘查區的選區起到輔助決策的作用。

在鈾礦勘查方面,松遼盆地是中國北方砂巖型鈾礦的主要產鈾盆地之一。近年來，在中國地質調查局天津地質調查中心的組織下，對松遼盆地北部油田資料進行二次開發和鉆孔原位驗證，在大慶長垣南端及周邊地區發現了多處鈾礦化富集區，并發現了工業鈾礦體，鈾礦找礦工作呈現了較大的突破與進展[1-2]。然而，目前對鈾礦異常的識別主要以地質理論和地質經驗為依據、線性數學方法作為基礎，分析給出鈾礦異常發生的臨界值，從而人工解譯得出期望的結果[3-6]。該層位是否為鈾礦異常主要依靠測井曲線的幅值大小來判斷，但實際的地質現象往往表現出非均質性的情況，難以用線性模型進行精確的描述與處理，存在較大的誤差[7]。人工識別存在精度不高，研究區內的適宜臨界值確定較為困難等問題。而精確的鈾礦礦體信息則需要專業的定量伽馬測井配合一系列放射性相關系數的校正和巖芯取樣信息來計算獲得[8]。礦體信息的獲取成本較高。因此，如何快速有效獲取精準的礦體信息成為鈾礦勘查的亟待解決的問題。

近年來，人工神經網絡技術在分類模式識別、劃分油氣層、巖性識別、預測儲層段參數等方面的應用廣泛[9]，并且該技術在識別礦物類型、沉積相的區分等方面應用效果良好[10]。在外國，Khandelwa等[11]通過BP(back propagation)神經網絡對密度和中子測井數據進行了預測，預測結果明顯優于多元回歸擬合；Baneshi等[12]選擇人工神經網絡進行巖石地球物理參數的估計，通過連續的三個BP神經網絡以較少的輸入參數較好的預測出了巖石孔隙度，降低了數據挖掘的時間和成本。在中國，陳科貴等[13]研究表明BP神經網絡模型相較于傳統測井解釋方法在雜鹵石分類識別中有明顯的優勢；朱紅等[14]提出基于ATD(自適應去噪)-BP神經網絡的頁巖氣產量預測方法，克服了儲層參數與氣井產量之間的非線性相關關系問題，較好地預測了氣井的產量；項云飛等[15]為應對線性回歸方法的不足，將神經網絡同線性回歸方法相結合對儲層孔隙度含水飽和度等進行劃分，結果表明神經網絡算法對于非線性問題的處理有較好的優勢。

綜上所述，神經網絡技術應用于數據預測、模式分類已較為成熟，可以適應非均質的地質條件和復雜多變的地質現象，發掘、學習并記憶地學數據之間的復雜關系，最終在相關問題的分析處理中得以運用。選擇人工神經網絡技術應用于大量的鈾礦鉆孔測井信息中，以BP神經網絡理論為基礎，構建適合的非線性數學模型，不斷優化約束條件，對鈾礦測井數據進行異常識別和提取。并通過與工業已知礦化層信息進行結果對比，對神經網絡模型的識別能力予以評價。

1 研究區鈾礦分布概況

研究區位于松遼盆地長垣南端某鈾礦礦集區，長垣南端屬松遼盆地北部中央坳陷區內的二級正向構造單元，東鄰三肇凹陷、朝陽溝階地，西接齊家—古龍凹陷，面積近420 km2[16]。研究區位置如圖1所示。

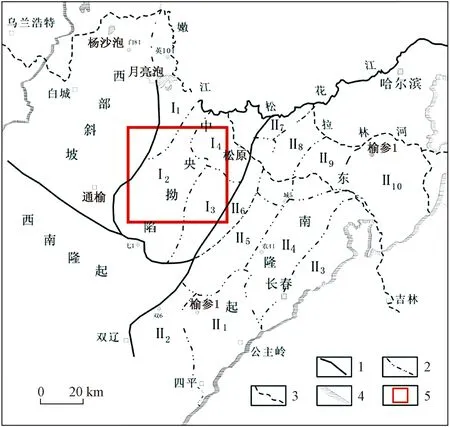
1為一級構造分區線；2為二級構造分區線；3為河流；4為盆地邊界；5為研究區圖1 研究區構造位置Fig.1 Tectonic location of the study area

松遼盆地是典型的陸相盆地，白堊系是松遼盆地最主要的賦油、鈾層系[16]。研究區內主要的含礦地層為白堊系的明水組與四方臺組。四方臺組底部與嫩江組呈平行不整合接觸，頂部與明水組呈整合接觸。四方臺組地層在盆地內廣泛發育，巖性以灰色、綠灰色中細砂巖，夾灰紅色、灰色粉砂巖、泥巖為主[17]。依據鉆孔測井數據以及前人巖芯取樣分析四方臺組為研究區內的鈾礦富集地層。

2 鈾礦異常的測井響應特征

研究區內的鈾礦異常主要賦存于四方臺組的砂體中，屬砂巖型鈾礦[1]。因而砂巖型鈾礦異常的測井響應特征主要有：極高的自然伽馬值(GR)，已知礦化層的平均放射性可達1 000 api；鈾礦異常多富集于泥-砂-泥結構、砂泥互層等，因而密度曲線在異常發生處有由大變小的趨勢，可在含礦目的層作為鈾礦異常存在的輔助標志；縮徑與擴徑現象的產生也對自然伽馬測井存在一定的波動影響，雖不屬于地球物理屬性，但其在放射性測井解釋中具有重要的輔助參數作用[18]。此外，由于鈾礦賦存巖性交替變化的原因，在鈾礦異常處表現出相較于上下巖層低電位、高電阻的現象。不同測井參數隨著鈾礦異常的發生出現各自的變化，這些變化間復雜且微小的相關關系共同指示著鈾礦異常的存在，同時也給鈾礦異常識別的準確性帶來了一定的困難。測井響應特征如圖2所示。

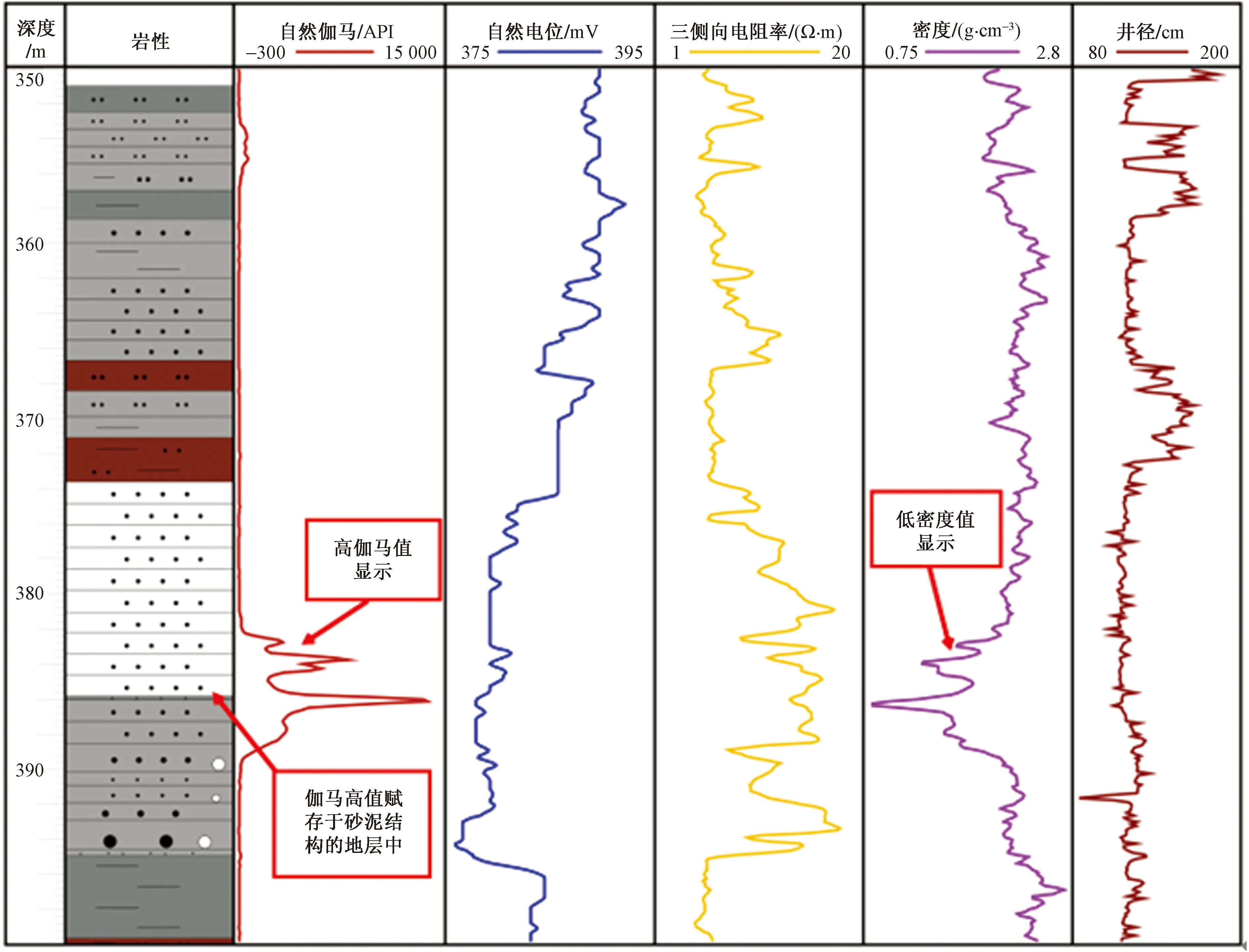
圖2 礦集區某鈾礦鉆孔測井柱狀圖Fig.2 Histogram of borehole logging of a uranium mine in a mining area

3 BP神經網絡模型的建立

人工神經網絡(artificial neural netwroks，ANN)方法就是利用生物仿生學觀點，探索人腦的生理結構，將對人腦的微觀結構及其智能行為的研究結合起來的一種認知方法[19]。在實際應用中，大多數的人工神經網絡模型是采用誤差反傳算法或其變化形式的網絡模型(BP神經網絡)[20]。BP神經網絡主要由輸入層、隱含層和目的層組成，每一層可包含不同的神經元個數，不同層之間傳遞的信號傳遞通過各層的權值和閾值共同作用，屬于前饋型神經網絡[20]。由于BP神經網絡智能化的信息處理，具有高效的模式識別能力，能夠學習和模擬任意的非線性變量的輸入輸出映射關系[21]。因此BP神經網絡模型適合于學習上述具有一定相關關系的測井數據，挖掘不同測井參數對于輸出的作用與貢獻，并對這種映射關系進行記憶并保存。

3.1 數據歸一化處理

輸入節點的數據來自不同的地球物理測井數據，均代表著不同別的物理意義，有著各自獨立的量綱，為了防止不同量綱之間的數值差異導致網絡訓練過程中陷入局部極小問題，需要對輸入數據進行歸一化，歸一化的方法較多，選擇極值歸一化作為數據預處理的方法。將歸一化后的測井數據作為神經網絡模型的輸入數據，其公式如式(1)所示：

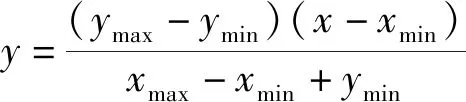
(1)

式(1)中：xmax、xmin分別為原數據的最大、最小值；ymax、ymin分別為歸一化后數據的最大、最小值[22]。

3.2 BP神經網絡原理

BP神經網絡包括信號的正向傳播和誤差的反向傳播兩個過程[17]。正向傳播時外部信息從輸入層傳入，經各隱含層逐層處理后，傳向輸出層，由輸出層接收隱含層的傳遞信息并加以處理得出實際輸出結果。若輸出層所得的實際輸出與期望的輸出不符，則模型轉入誤差的反向傳播階段。在誤差反向傳播時依據神經網絡的梯度下降算法，沿梯度下降最快的方向將誤差分攤給所有神經元，根據所分攤的誤差不斷調整網絡的權值和閾值，優化網絡的約束條件，使網絡的誤差平方和達到最小，以滿足網絡預設的目標條件[19]，其主要過程如下。

3.2.1 變量和參數的定義

BP神經網絡模型的輸入參數為數據預處理后的歸一化矩陣，即為矩陣X。

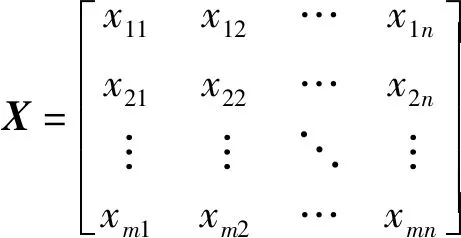
(2)

式(2)中：總計m個樣本,n個變量即為m×n的矩陣向量，可表示為X=(x1,x2,…,xn)。初始權值為ωih，由隱含層到輸出層的權值為ωho。隱含層神經元閾值為bh，輸出層神元閾值為bo，隱含層神經元數為p，輸入為hi，輸出為ho；輸出層神經元數為q，輸入為yi，輸出為yo；樣本個數為k=1,2,…,m,激活函數為f,誤差函數為

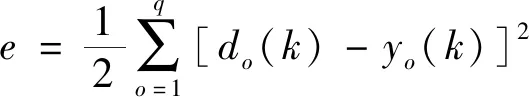
(3)

式(3)中：e為誤差函數；do(k)為因變量的預測值；yo(k)為因變量的實際值。

3.2.2 網絡初始化

給各連接權值分別賦一個區間(-1，1)內的隨機數,設定誤差函數e，給定計算精度值ε和最大學習次數M。隨機選取第k個輸入樣本及對應期望輸出為

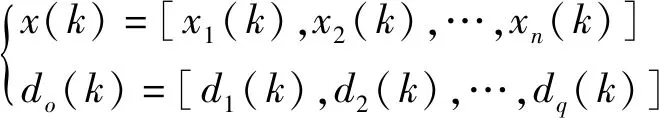
(4)

3.2.3 根據訓練樣本計算各層輸入輸出

隱含層的輸入輸出分別為

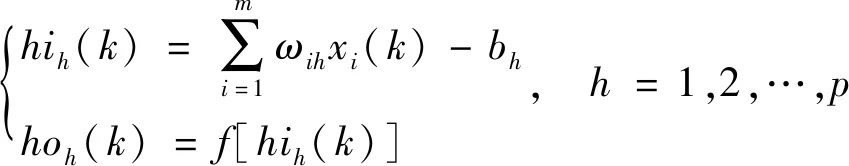
(5)

式(5)中：hih(k)為隱含層第h個神經元的輸入值；hoh(k)為隱含層第h個神經元的輸出值。

輸出層的輸入和輸出分別為

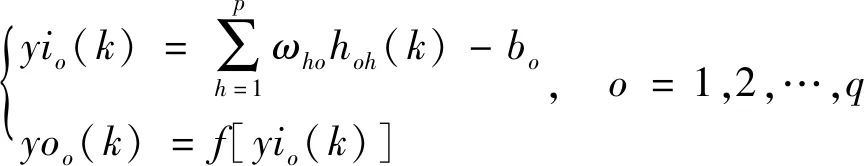
(6)

式(6)中：yio(k)為輸出層第o個神經元的輸入值；yoo(k)為輸出層第o個神經元的輸出值。

3.2.4 根據預設目標求解神經元偏導數

利用網絡期望輸出和實際輸出，計算誤差函數對輸出層的各個神經元的偏導數，輸出層神經元的偏導數為

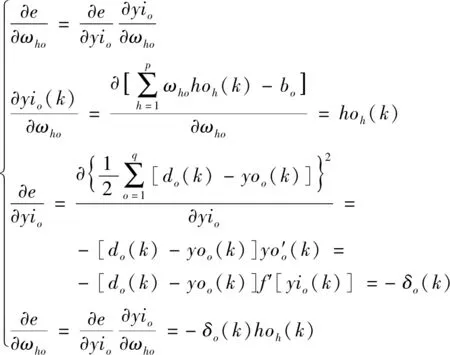
(7)

式(7)中：h取值于p，p為隱含層神經元的個數；o取值于q，q為輸出層神經元的個數；δo(k)為誤差對輸出層第o個神經元輸出值的偏導數。

同理計算誤差函數對隱含層各個神經元的偏導數：

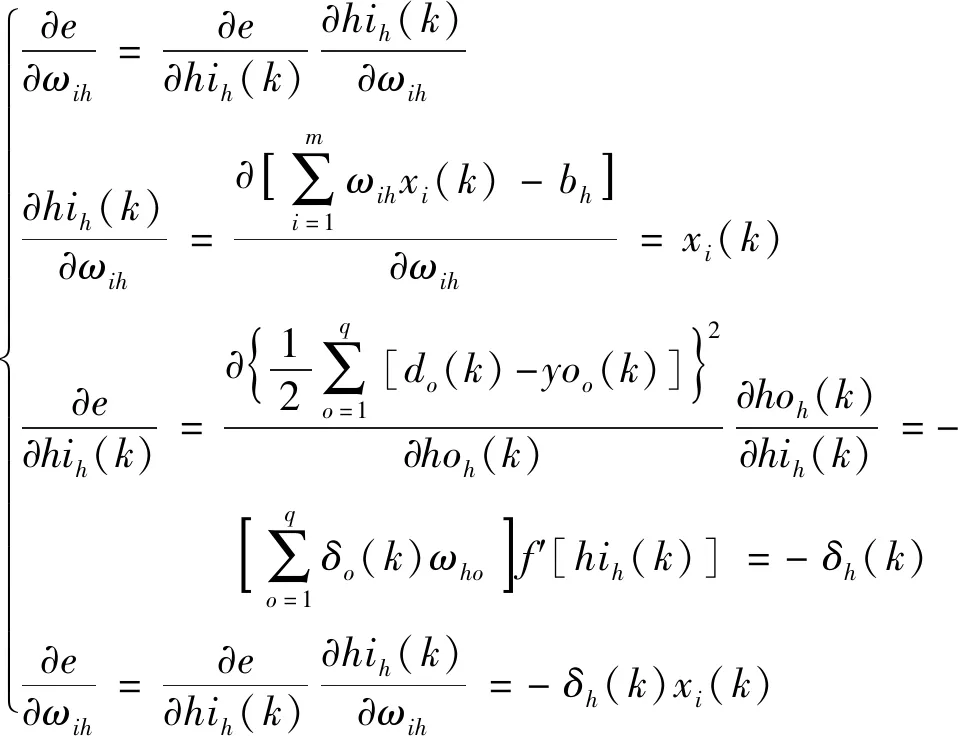
(8)

式(8)中：i取值于m，m為樣本個數；-δh(k)為誤差對隱含層第h個神經元輸出值的偏導數。

3.2.5 權值修正

利用輸出層和隱含層各神經元的偏導數和隱含層各神經元的輸出來修正各層的連接權值：

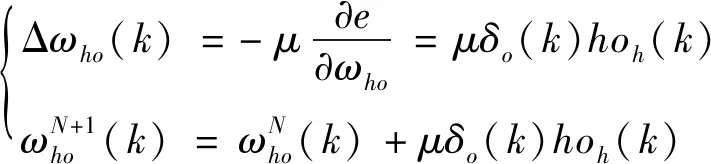
(9)

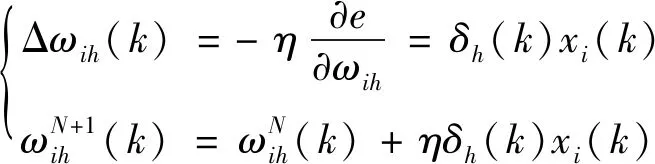
(10)

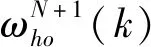
3.2.6 計算全局誤差

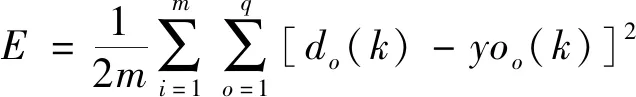
(11)

式(11)中：E為全局誤差；m為樣本個數；q為輸出層神經元個數。

3.2.7 誤差檢驗

判斷網絡全局誤差是否滿足網絡模型的預設要求。當誤差達到預設要求或學習次數達到預設的最大次數，則模型算法結束。否則，選取下一個學習樣本及對應的期望輸出，返回到3.2.3節，進入下一輪學習,直至目標達成方可終止。

3.3 測井參數優選及模型結構設計

根據鈾礦異常的基本測井響應特征為原則，選取5條相關的地球物理測井曲線來進行鈾礦異常的BP神經網絡建模，分別為自然伽馬(GR)、自然電位(SP)、密度(DEN)、三側向電阻率(LLS)以及井徑(CAL)5條測井曲線，具體數據如表1所示。

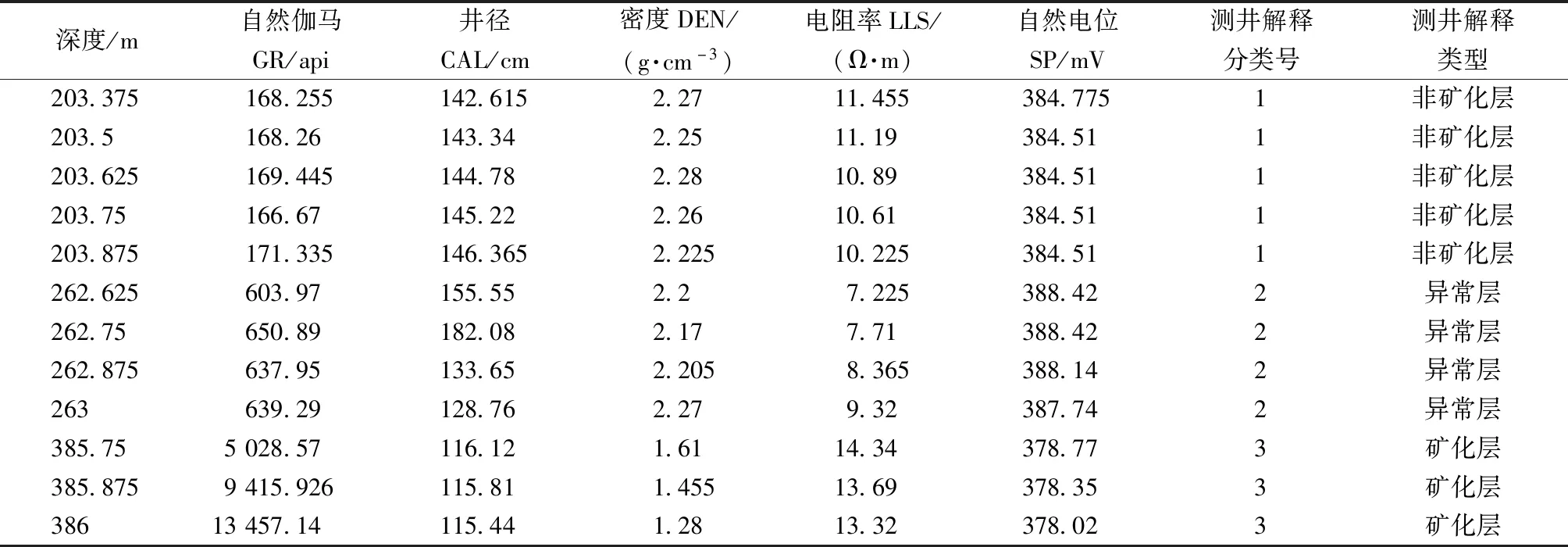
表1 BP神經網絡模型樣本數據Table 1 BP neural network model sample data

以這五條測井曲線預處理后的數值作為BP神經網絡模型的外部輸入信息，輸入層共計5個節點，隱含層的層數和節點數目則需要結合輸入節點、輸出節點共同決定，根據礦集區已知礦體信息，鈾礦異常層分為兩類，邊界品位為0.005%～0.01%的層位被界定為異常層，邊界品位大于0.01%的層位則定義為礦化層。BP神經網絡的輸出節點即為異常信息的識別結果，共計礦化層、異常層、非異常層3個節點。而在隱含層方面，理論上單層的隱含層配合線性的傳遞函數在神經元數足夠多的情況下可以無限逼近任何非線性函數，增加隱含層層數可以降低網絡誤差，提高精度，但同時也會導致網絡復雜化，從而增加了網絡的訓練時間和出現過擬合的傾向[20-21]。因此綜合輸入輸出節點信息，初始隱含層選擇單層結構，隱含層神經元節點數依據映射網絡存在定理(Kolmogorov)來確定：

z=2t+1

(12)

式(12)中：z為隱含層節點數;t為輸入層節點數[22]。

根據經驗公式選定初始隱含層節點數為11個，在后續的誤差反傳計算過程中間依據達到網絡目標的目的，采用逐次加減的方法來尋找最適宜的隱含層節點數，實現網絡的結構的優化[19]。

在變量優選和數據預處理的基礎上，構建三層BP神經網絡模型對砂巖型鈾礦異常進行預測。神經網絡結構如圖3所示。

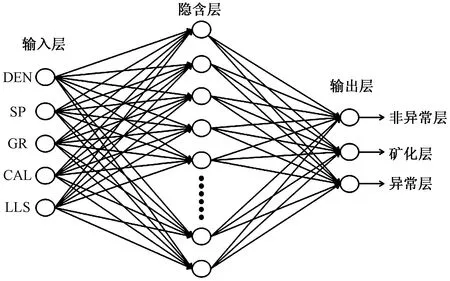
圖3 BP神經網絡結構示意圖Fig.3 Schematic diagram of BP neural network structure

4 識別結果與分析

使用MATLAB R2016a軟件進行BP神經網絡模型的構建，以研究區已探明鈾礦礦體的4個鈾礦鉆孔地球物理測井數據含礦目的層信息為訓練樣本，訓練樣本的點位選取也要考慮礦化信息的典型性，同時滿足空間位置的選取均勻性，建立5×11×3結構的BP神經網絡模型，預設最大學習次數為20 000次，學習率為0.05，目標最小均方誤差為1×10-6。并對模型區數據進行反復訓練并保存網絡，使得網絡對于模型區的輸入輸出映射關系存儲并記憶。利用所訓練模型對研究區內的其他4口鈾礦鉆孔進行測試，并將最終的測試結果同已探明礦體信息進行驗證對比，具體情況如圖4所示。

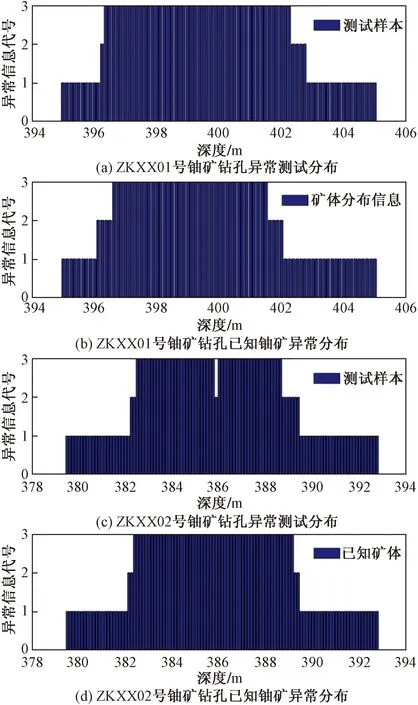
1為非異常層；2為異常層；3為礦化層圖4 測試結果分析對比Fig.4 Comparison and analysis of test results

圖4為ZKXX01號鉆孔中395～405 m段，ZKXX02號鉆孔379～393 m段鈾礦鉆孔測井數據異常識別結果，經過對測試數據的統計分析對比，ZKXX01和ZKXX02號鉆孔的測試總體準確率分別為83.95%和93.4%，總體效果較為顯著。根據放射性測井規范中對異常的定義，泥巖層為自然伽馬放射性最高的巖層，其平均值為150～170 API，選擇200 API為砂巖型鈾礦異常的界定閾值，篩選砂巖型鈾礦異常以作對比。由圖5可知，模型識別精度較高，所識別結果能包含大部分的已知礦體信息，相較于傳統異常判別方法更接近礦體的形態和范圍。在研究區內選擇4口鈾礦鉆孔進行測試分析，并統計對比測試結果。4口鈾礦異常識別結果如表2所示,單井的識別深度對比如表3所示，其全體測試樣本平均準確率可達86.55%。

結合4口井的情況來看，綜合ZKXX-02號鈾礦鉆孔深度對比信息表(表3)。若單以異常樣本(礦化層本身也屬于鈾礦異常)被判別準確的標準來看，BP神經網絡模型對異常的識別準確率會高于模型整體的識別率，在模型識別的算法中，存在對非含礦層的判別及對比。異常層的判別范圍較大必然會導致非礦化層的判別錯誤，所以異常層的識別準確率較之模型整體更高。

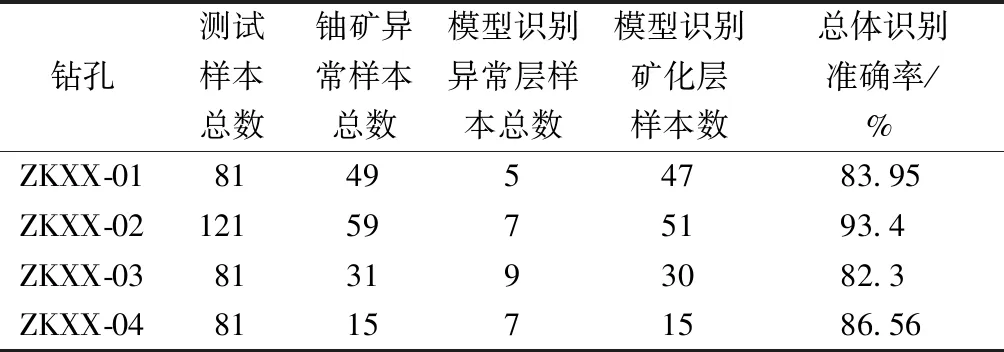
表2 鈾礦異常識別結果統計Table 2 Statistic of uranium anomaly identification results

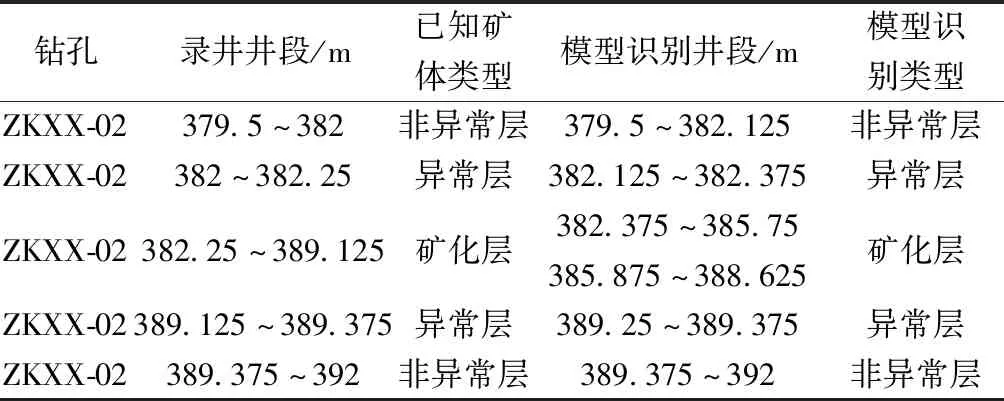
表3 ZXXX-02號鉆孔識別深度結果對比Table 3 Comparison of drilling depth identification results of ZXXX-02

測試樣本的選取一般為含礦目的層10 m左右的一段測井數據，所選取的測井參數均為同鈾礦異常相關的地學屬性，通過已知樣本的不斷學習，神經網絡模型可以記憶已知礦體信息同測井數據之間錯綜復雜的規律，并將其應用于對應得模式識別，對鈾礦異常的識別是有效的。神經網絡技術是基于數據樣本的學習技術，因此對于模型輸入數據的要求較高，運用大尺度的整鉆測試數據會數據不穩定性導致模型精度下降，這是由于不同層位下的地質條件及其巖性物性差異所導致，故針對含礦目的層進行已知鈾礦異常的建模，相較于臨界值異常判別，能綜合多屬性信息對未知孔的鈾礦異常信息給出準確判斷，對于鈾礦資源預測、找礦方向選擇等工作不失為一種快速高效的異常識別方法。

5 結論

應用BP神經網絡模型對松遼盆地某鈾礦礦集區進行了鈾礦異常識別，通過對比分析得出以下結論。

(1) 依據砂巖型鈾礦異常的測井響應特征，運用BP神經網絡模型識別并提取出鈾礦異常的兩種類型，即鈾礦的異常層和礦化層，識別準確率達到86.55%。模型識別結果同已知鈾礦異常信息重合度高。

(2) 基于BP神經網絡模型的異常識別方法為鈾礦找礦的實際工作提供一種新思路，一種基于機器學習的識別方法。在實際應用中異常識別的效果顯著，識別速度快，方法可靠且能消除人為工作的偶然誤差，識別效果較好。

地球物理測井資料的獲取相對而言成本較高，難以對研究區內的全體樣本均進行精確的測量與分析，因此利用好現有的優質數據便顯得尤為重要。利用BP神經網絡訓練并發掘測井數據中的異常信息能大大降低信息獲取的成本和時間，極大地提高找礦工作的效率，目前利用神經網絡處理地學分類問題，由于同一礦集區地質條件總體相似，利用已知鉆孔的礦化層信息為模型，充分利用多個測井屬性信息，對異常劃分進行分類。后續也可利用神經網絡、支持向量機等機器學習方法對預測問題提出相應的解決方案。在已有大量已知礦化體信息的情況下，可利用礦化體的品位、平米鈾量等更為精確的測量信息進行建模，對未知孔進行關于品位、平米鈾量等屬性的數值預測，能夠在礦產資源量預測、成礦遠景區規劃等方面提供有力的輔助決策支持，可作為進一步的研究方向。