蠕變作用下埋深對結構受荷特征影響分析
——以廣佛環線東環隧道工程為例

周 坤，陳 龍

(1.中鐵第四勘察設計院集團有限公司，武漢 430063；2.西南交通大學交通隧道工程教育部重點實驗室，成都 610031)

近年來，伴隨著中國經濟水平的飛速發展和隧道工程施工工藝技術的進步，中國已經成為當今世界上隧道及地下工程規模最大、數量最多、地質條件和結構形式最復雜、修建技術發展速度最快的國家[1]。

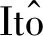
基于此，以廣州東環隧道為背景，運用FLAC3D有限差分軟件研究蠕變作用下埋深是如何影響管片襯砌的變形和受力特性，以期對后續深埋軟巖隧道的長期受荷和變形取值提供經驗和依據。

1 工程概況

依托廣佛環線廣州南站至白云機場段東環隧道大源站—太和站區間盾構隧道工程展開相關研究工作。該項目位于珠江三角洲中部，西連佛肇城際，東接佛莞城際，同時銜接佛莞線、穗莞深線、廣惠線、廣清線、佛肇線和廣佛江珠6條城際線路，是珠三角城際軌道交通網及廣佛環線的重要組成部分。其中，廣佛東環隧道大源站—太和站區間隧道工程位于廣州市白云區太和鎮，為雙線鐵路隧道，隧道主要采用盾構法施工，建筑長度6 804 m，區間盾構隧道總長5 987 m。隧道主體結構采用單層裝配式通用管片環，混凝土強度等級為C50，抗滲等級P12。管片襯砌外直徑8.8 m，厚400 mm，環寬1.8 m，采用“6+1”分塊模式，具體為4B(56.84°)+2L(56.84°)+F(18.96)，其中B為標準塊，L為鄰接塊，F為封頂塊，管片結構分塊情況如圖1所示。

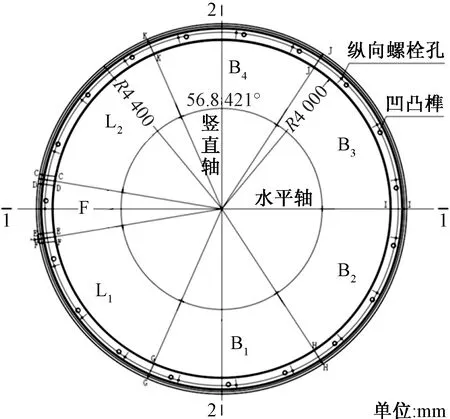
圖1 盾構法隧道管片結構分塊圖Fig.1 Block diagram of shield tunnel structure

依托工程隧址區多為丘陵與丘間谷地，屬丘陵地貌，地勢起伏較大，地面高程21～135 m，隧道埋深十余米至上百米不等，最大覆土厚度超過130 m。其中盾構隧道長距離下穿不同風化程度的片麻巖、炭質板巖、粉砂巖、泥質砂巖等，圍巖風化程度高、強度差異較大、滲透性差異顯著，為目前中國首次采用盾構隧道的方式長距離穿越大埋深巖層，區間隧道地質縱斷面如圖2所示。

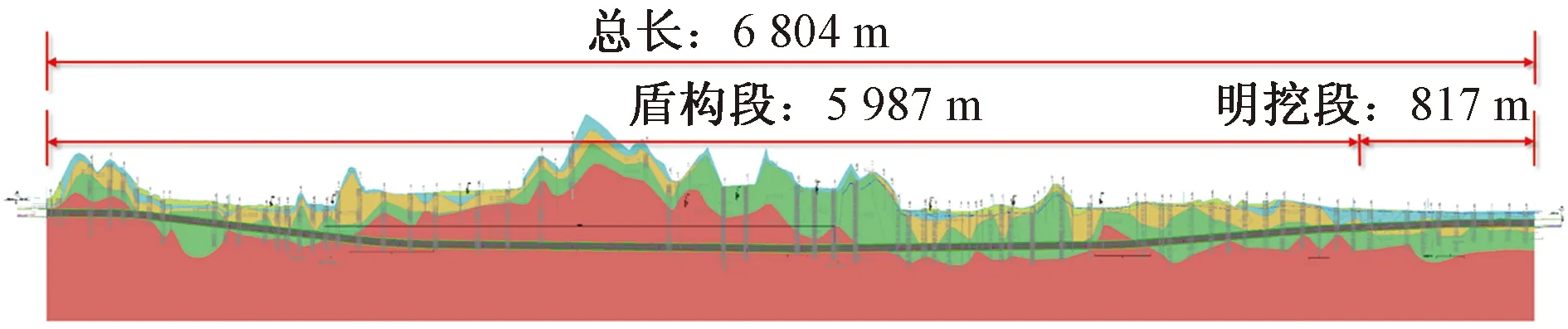
圖2 隧道穿越巖層斷面圖Fig.2 Cross section of tunnel through rock formation

2 數值分析模型

對于大埋深軟巖盾構隧道，在地應力作用下當巖體發生持續的流變行為特征后，隧道開挖后圍巖的塑性區范圍會進一步發展，管片結構所承受的圍巖形變壓力隨時間變化而逐漸增大，進而導致將結構變形和內力的增加。因此，利用數值仿真的方法研究圍巖蠕變作用下不同埋深軟巖盾構隧道結構受荷特征。

2.1 基本假定

結合FLAC3D有限差分軟件的功能特征，在進行模型建立和荷載分析時做如下假定。

(1)不考慮深埋巖體的各項異形特征，將隧道圍巖視為結構部均勻的各項同性連續介質。

(2)模型中不考慮地下水對盾構隧道結構的荷載作用和對圍巖力學特性軟化的影響，取自然含水狀態巖石力學參數為計算參數。

(3)現場得到的巖體試樣室內力學試驗的結果都是可信的，可以反映在地應力條件下的應力特征，且根據試驗結果的巖體參數可以用于數值模型中。

(4)對于所考慮的隧道埋深情況，建立模型時只考慮地層的自重應力場。

(5)盾構隧道每一施工步的時間較短，巖體實際發生蠕變行為較弱，因此在建立模型時不考慮盾構隧道每一施工步的圍巖蠕變行為，僅考慮盾構隧道開挖完成后的圍巖長期蠕變行為。

2.2 數值模型

圖3 數值計算分析整體模型Fig.3 Numerical calculation analysis of the overall model

在2.1節合理假設的基礎上，利用FLAC3D軟件建立考慮盾構施工過程的大埋深隧道三維數值模型如圖3所示。一般認為數值模型邊界與隧道邊界的距離取其洞徑的3倍以上時可不考慮模型邊界效應影響，因此建模時為了減小模型計算的邊界效應，取隧道中心與模型四周邊界的距離均為50 m，在模型縱向上考慮盾構開挖及管片襯砌施作的施工過程影響取縱向距離為90 m(50環)，即計算模型的尺寸為100 m(x)×100 m(z)×90 m(y)。邊界條件中模型四周及底面采用法相位移約束條件，并考慮隧道埋深條件和地應力場分布在模型上表面和模型內部單元施加相應的構造應力以模型地層真實的自重應力場。

2.3 模型相關參數

2.3.1 隧道圍巖參數

數值模型中隧道圍巖采用正六面體實體單元模擬，根據假定條件在模擬盾構隧道施工過程中不考慮圍巖蠕變特性，則巖體為理想彈塑性體，遵循Mohr-Coulomb屈服準則。在模擬圍巖長期蠕變行為時，巖體的蠕變模型采用FLAC3D軟件中可以模擬巖土體黏彈、黏性、黏塑行為的Cvisc模型。計算模型中所采用圍巖力學參數如表1所示。

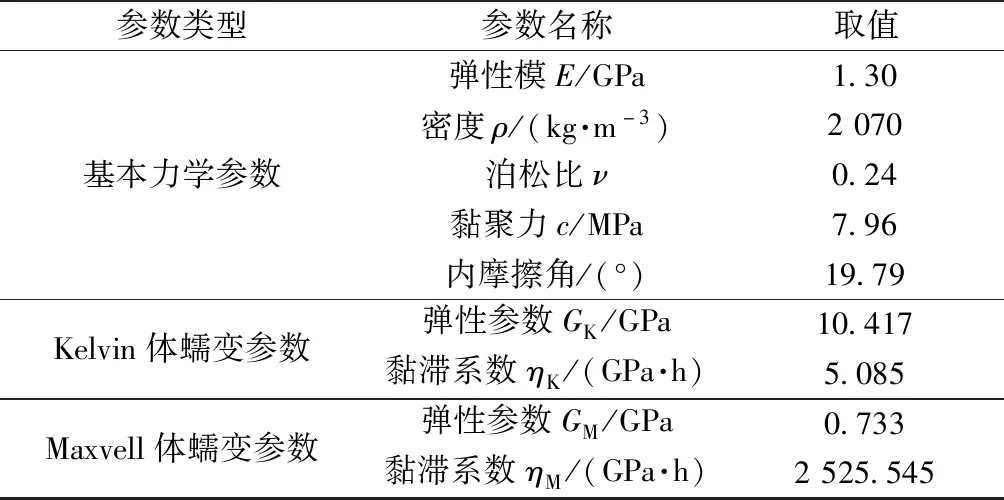
表1 隧道圍巖計算力學參數Table 1 Calculation of mechanical parameters of tunnel surrounding rock

2.3.2 盾構隧道相關組參數

為了對盾構隧道的施工過程進行模擬，數值模型中分別對與盾構掘進施工相關的主要結構構件進行了模擬。依托工程廣佛環線東環隧道的盾構機結構如圖4所示，其中盾殼分前盾、中盾、和后盾三部分，各部分的半徑依次略有縮小，盾殼整體呈錐形特征分布，而建模時做簡化處理，將其考慮為圓柱形結構。盾構隧道主要結構構件的參數如表2所示。

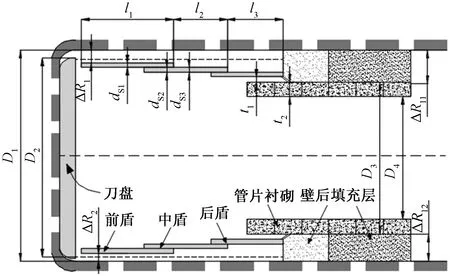
圖4 依托工程盾構機形式示意圖Fig.4 Schematic diagram of the form of the shield machine

2.3.3 層間模擬及接觸面接觸參數

(1)interface界面單元基本理論：圖5為FLAC3D軟件中interface界面單元、節點和節點接觸面積和本構模型的示意圖，其中Kn為法向剛度，Ks為剪切模量，每一個四邊形的區域都有兩個接觸單元定義，接觸面本構關系服從Coulomb抗剪強度準則。

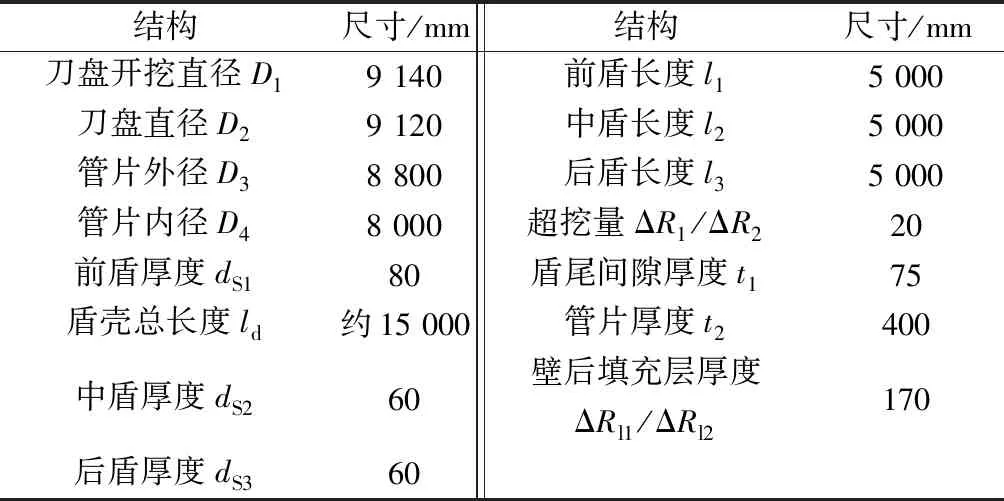
表2 盾構主要結構組件的幾何尺寸Table 2 Geometric dimensions of the main structural components of the shield

在利用FLAC3D軟件中的接觸單元進行計算時，interface接觸面的節點會對接觸面的變形進行探測，并通過圖5所示的本構關系來表示接觸面單元的實際關系，其中法向剛度Kn和剪切剛度Ks是表示接觸面單元特征的重要參數。Kn和Ks取值過大會導致計算響應和收斂速度慢，并可能產生與相關的數值誤差。FLAC3D軟件的用戶手冊中給出了法向剛度Kn和剪切剛度Ks的經驗選取方法[15]。

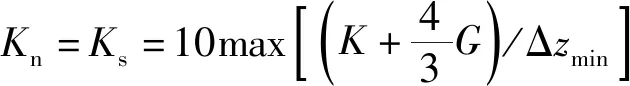
(1)

式(1)中：K為體積模量；Kn為法向剛度；Ks為剪切剛度；G為剪切模量；Δzmin為接觸面法向方向上連續區域的最小尺寸。

(2)模型中的接觸面單元：計算模型中，刀盤的擴挖使得盾構機盾殼與隧道圍巖之間存在超挖間隙，為了模擬出盾構超挖作用對圍巖土體的卸荷作用，在層間設置了接觸單元。為了求得管片結構所受到的圍巖荷載作用，在管片與壁后注漿層之間設置了層間接觸單元。兩處的層間接觸單元都采用FLAC3D軟件中的interface接觸單元模擬，且根據軟件中接觸面單元的特點和要求，將接觸面應連接到密度較大的網格上，得到計算模型中的接觸面如圖6所示。

圖6 計算模型中的接觸面單元Fig.6 Contact surface unit in the calculation model

2.3.4 計算模擬流程

利用數值模型進行數值計算時，根據施工階段對盾構隧道的施工全過程進行模擬。相應的施工模擬過程及計算步驟如下。

Step1計算初始地應力場。根據隧道埋深對模型施加地層自重應力場，設置模型邊界條件，進行平衡計算。

Step2盾構進洞計算模擬。在模型中進行盾構掘進和土體開挖模擬，施加掌子面推力并激活盾殼單元與盾殼處接觸面單元，模擬盾構機的進洞行為。這一階段過程如圖7(a)所示。

Step3盾構隧道正常掘進施工模擬。待盾殼完成進入地層即盾構機完成進洞行為后，模擬盾構機向前推進過程，同時激活盾構管片和壁后注漿層單元。這一階段過程如圖7(b)所示。

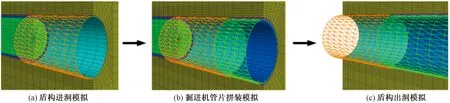
圖7 盾構隧道施工模擬示意圖Fig.7 Schematic diagram of shield tunnel construction simulation

Step4盾構隧道出洞模擬。待模型中盾殼到達模型邊界時，盾構繼續推進，并在盾尾激活管片和填充層單元直至完成全部管片拼裝模擬。過程如圖7(c)所示。

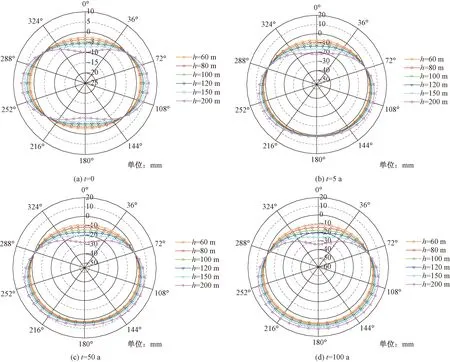
圖8 不同埋深下管片襯砌徑向變形Fig.8 Radial deformation of segment lining under different buried depths

Step5圍巖蠕變行為模擬。將模型中圍巖土體設置為Cvisc模型，賦予表1中的巖體蠕變參數，進行蠕變計算。蠕變計算時首先需要打開FLAC3D軟件中的蠕變計算模塊，并設置蠕變計算的時間步長等量值。利用FLAC3D軟件進行蠕變計算分析時的詳細理論可以參考文獻[19]。

3 不同埋深下結構受荷特征分析

在僅考慮巖體自重應力場的情況下，隨著埋深的增大巖體賦存環境的地應力越大，隧道開挖后圍巖的變形和應力作用越明顯。在考慮圍巖蠕變效應的情況下，地層應力越大，巖體在應力作用下產生的蠕變變形越大，且當地層應力超過巖體的強度限制時，隧道開挖后圍巖將發生加速蠕變行為，從而對隧道支護結構產生危害。鑒于此，結合依托項目的工特點，研究蠕變作用下隧道不同埋深對結構受荷特性的影響，設計了埋深h=60、80、100、120、150、200 m工況進行分析。

3.1 模型相關參數

根據數值結果得到圍巖蠕變時間t為0、5、50、100 a后不同隧道埋深下管片襯砌的徑向變形，如圖8所示(徑向變形量值以向管片外側為正，向內側為負)。

前者生成的空調系統在設備特征中存在數據理想化的問題，在管路布置中存在偏差。接下來，分別對兩者進行修正，并對系統進行圖示化處理。

由圖8可知，隨埋深的增大，管片襯砌整體變形更加顯著，變形趨于不利。當不考慮圍巖蠕變效應時(t=0)，隨埋深增大，管片襯砌拱頂沉降逐漸增加，拱底隆起變形逐漸增大；考慮圍巖蠕變效應后，管片襯砌整體發生沿豎向向下的變形，拱底由隆起變形而逐漸變為沉降變形。

圖9 不同埋深下管片襯砌彎矩分布Fig.9 Distribution of bending moment of segment lining under different buried depths

現以拱頂豎向位移為例，得到圍巖蠕變5 a和100 a時位移的變化情況如表3所示。由表3可知，圍巖衰減蠕變階段拱頂豎向位移變化率遠大于穩定蠕變階段，圍巖蠕變過程中管片襯砌位移的變化率隨著埋深的增加逐漸增大，埋深越大管片襯砌的變形發展越顯著。

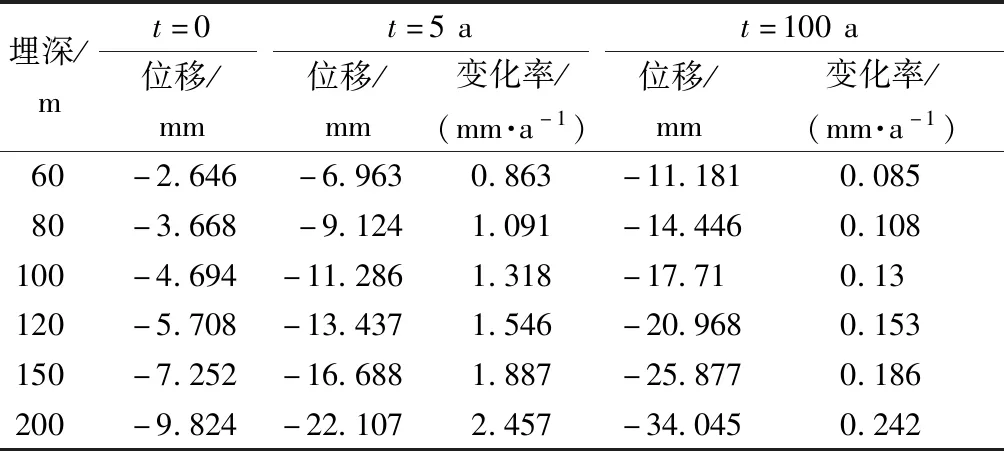
表3 各工況下拱頂豎向位移變化情況Table 3 Changes in vertical displacement of the dome under various working conditions

3.2 管片結構內力分析

彎矩和軸力是進行結構受力分析常用的量值，通過FLAC3D內置的Fish語言提取圍巖蠕變過程中不同埋深隧道管片襯砌的彎矩如圖9所示。

如圖9所示，在各個計算工況下管片襯砌的彎矩分布規律基本相同，即拱頂和拱底受負彎矩，兩側拱腰受正彎矩；埋深越大管片襯砌所受的最大正彎矩和最大負彎矩均增大。根據圖9中的彎矩分布結果，得到圍巖蠕變過程中管片襯砌最大正彎矩和最大負彎矩隨埋深的變化情況如表4所示。

由表4可知，隧道埋深越大，管片襯砌的正、負彎矩也越大圍巖蠕變過程中管片襯砌正、負彎矩極值的變化也越明顯，結構受圍巖蠕變作用的影響越大。

同上，根據數值計算結果得到圍巖蠕變0、5、50、100 a時不同埋深隧道管片襯砌的軸力分布如圖10所示。由圖10可知，管片襯砌拱腰處軸力最大，拱頂和拱底處軸力較小。隨埋深增大，管片襯砌軸力圖呈向外擴展的趨勢，其軸力值越大。考慮圍巖蠕變效應后，不同埋深下軸力的分布特征和施工完成后(t=0 a)的分布特征相同。

圖10 不同埋深下管片軸力分布Fig.10 Axial force distribution of segments under different buried depths

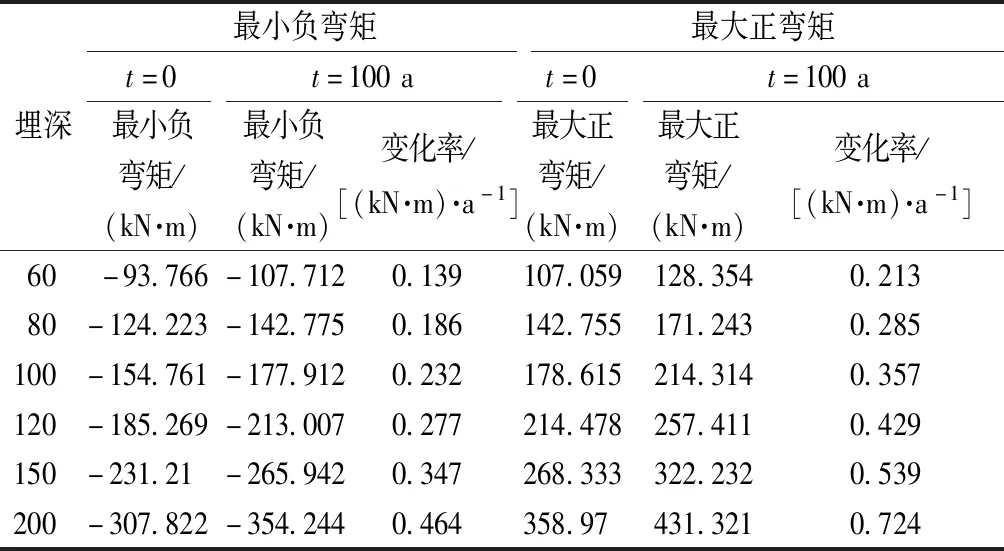
表4 蠕變過程中不同埋深工況下管片襯砌彎矩變化情況Table 4 Variation of bending moment of segment lining under different buried depth conditions during creep process

為了更加直觀的研究隧道埋深對管片襯砌軸力影響，根據計算結果得到圍巖蠕變過程中管片襯砌軸力極值的變化情況如表5所示。

結合表5中圍巖蠕變過程中管片襯砌軸力極值的變化數據，可知在圍巖衰減蠕變階段管片襯砌的軸力變化較大，而在穩定蠕變階段軸力緩慢變化；管片襯砌的最大軸力值隨隧道埋深的增加而逐漸增大，且埋深越大軸力的變化率越大。

3.3 管片襯砌接觸壓力分析

利用管片襯砌和填充層之間的接觸壓力來分析圍巖對管片襯砌的荷載作用，得到圍巖蠕變過程中不同隧道埋深下管片襯砌拱頂和拱腰處的接觸壓力變化曲線如圖11所示。由圖11可知，圍巖蠕變過程中不同埋深下管片襯砌外側接觸壓力的變化規律與變形及內力的發展規律相同存在兩個變化階段。

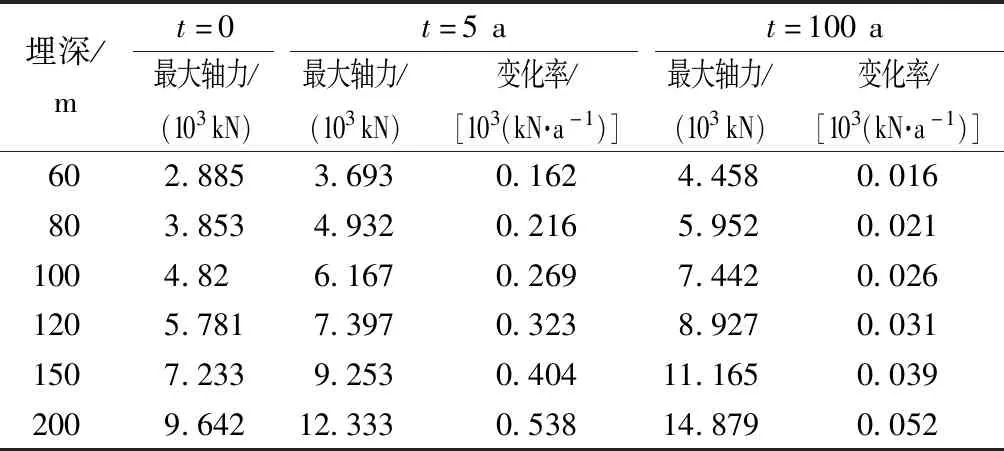
表5 不同埋深下管片襯砌軸力極值變化情況Table 5 Variations of axial force extreme values of segment lining under different buried depths

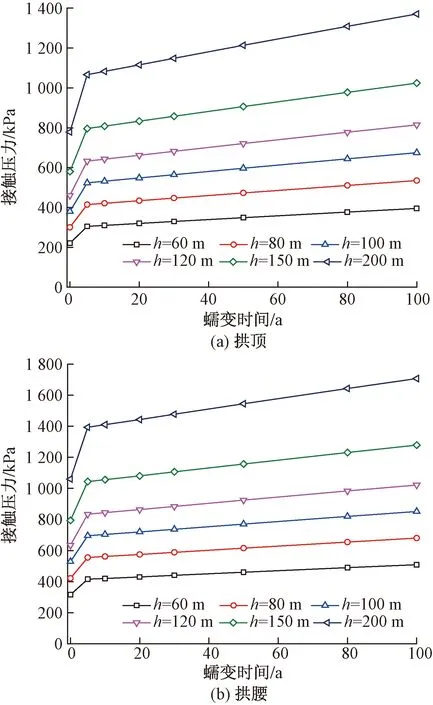
圖11 不同埋深下洞周接觸壓力變化曲線Fig.11 Curve of contact pressure around the hole at different depths

根據該圖的數據可知，隨隧道埋深的增加，管片襯砌外側接觸壓力逐漸增大，結構受地層圍巖壓力的作用越顯著；圍巖蠕變效應引起管片襯砌受荷作用增強，以拱頂處接觸壓力為例，在圍巖蠕變100 a的時間里，60、80、100、120、150、200 m埋深隧道接觸壓力分別增加了174.567、234.556、294.342、354.059、443.447、592.006 kPa，說明隧道埋深越大，相同時間內管片襯砌接觸壓力的變化率更大，結構受荷受圍巖蠕變的影響更顯著。

4 結論

建立考慮盾構隧道施工全過程的數值分析模型，分析了圍巖蠕變作用下的大埋深盾構隧道管片結構受荷特性，并從軟巖隧道賦存應力場環境方面研究了圍巖蠕變作用下隧道埋深對管片結構變形、內力和接觸壓力的影響。主要研究結論如下。

(1)開挖初期，隧道頂部圍巖沉降，底部發生隆起，在考慮圍巖的蠕變效應后，管片襯砌整體發生沿豎向向下的變形。隨隧道埋深的增大，管片襯砌整體變形越發顯著，圍巖衰減蠕變階段的拱頂豎向位移變化率遠大于穩定蠕變階段。

(2)隨隧道埋深的增大，彎矩與軸力、接觸壓力均逐漸增大，在蠕變過程中管片襯砌受荷特征受巖體蠕變的影響也越大。在巖體未發生加速蠕變的情況下，圍巖蠕變過程中管片襯砌的內力和接觸壓力的變化規律基本相同，有衰減蠕變和穩定蠕變兩個階段。