基于Savitzky-Golay濾波的雙向門控循環單元神經網絡汽輪機熱耗率預測

馬良玉，王永軍

(華北電力大學控制與計算機工程學院，保定 071003)

汽輪機熱耗率是指每產生1 kW·h電能消耗的熱量，通常作為反映機組運行熱經濟性的一項重要指標[1]。目前，汽輪機熱耗率作為監測機組性能的重要方式得到了各電廠的普遍重視，準確預測熱耗率對汽輪機組的安全、經濟運行和優化控制具有重要的工程意義。汽輪機熱耗率在機組運行過程中受到眾多因素的影響，且各因素之間具有較強的耦合性和非線性，傳統的機理建模方法很難滿足現場的實際需求。隨著人工智能技術的發展，汽輪機熱耗率預測模型的研究取得了顯著成果。張文琴等[2]采用偏最小二乘算法建立了汽輪機熱耗率回歸模型。牛培峰等[3-4]采用各種智能優化算法對快速學習網等建模算法的參數進行優化，并建立相應的熱耗率預測模型。王惠杰等[5]采用偏相關分析法確定了汽輪機熱耗率的主要影響因素，并將其作為黑箱模型的輸入參數，建立了基于FOA-LSSVM算法的熱耗率預測模型。李輝[6]采用在線支持向量回歸算法建立了汽輪機熱耗率回歸模型，能夠很好地適應在線應用。這些建模方法都取得了一定的預測效果，但由于沒有充分考慮時序數據的時間相關性，對模型的預測精度產生了一定影響。

人工神經網絡(artificial neural network,ANN) 具有很強的非線性函數擬合和自適應學習能力，有效解決了機理建模過程中計算量大和精度低等問題[7]。傳統神經網絡算法具有易陷入局部最優解、出現過擬合以及處理時序數據能力較弱等不足。循環神經網絡[8](recurrent neural network,RNN)具有獨特的自循環機制，能夠將過去的信息用于當前的預測，有效解決了時間序列的依賴問題。門控循環單位(gated recurrent unit,GRU)網絡是一種改進的循環神經網絡，其特殊的網絡結構能夠有效保證信息在網絡自循環中的傳遞，緩解傳統循環網絡因梯度消失帶來的性能損失[9]。

火電廠機組運行是一個動態過程，針對傳統建模方法沒有充分考慮時序數據時間相關性的問題，借助某1 000 MW火電機組采集的真實歷史數據建立汽輪機熱耗率的雙向GRU神經網絡預測模型，并通過與其他算法建立的預測模型進行對比驗證該模型的預測精度和魯棒性。

1 GRU神經網絡原理

1.1 循環神經網絡

BP(back propagation)神經網絡等前饋神經網絡中的信息為單向傳遞，沒有考慮數據之間的時序相關性，在一定程度上限制了網絡模型的預測性能[10-11]。循環神經網絡具有短期記憶功能，能夠反映歷史信息對當前狀態的影響，更符合生物神經網絡的結構。圖1為典型的循環神經網絡結構。圖1中，xt和ot分別表示t時刻的網絡輸入和輸出;ht為隱含層t時刻的狀態;A為RNN的神經元。

o為網絡輸出；W、U分別為各層對應的權值圖1 典型循環神經網絡結構圖Fig.1 Typical recurrent neural network structure

數據樣本的信息在循環神經網絡中有兩條傳遞方向：①由輸入層到隱含層再到輸出層的單向傳遞；②由隱藏層到隱含層形成的閉環傳遞，構成自連接的記憶單元。RNN 的計算公式如式(1)、式(2)所示：

ht=tanh(Uxt+Wht-1+bt)

(1)

ot=softmax(Vht)

(2)

式中：U、W和V分別為各層對應的權值，b為偏置；tanh( )和softmax( )為非線性激活函數。

理論上傳統循環神經網絡能夠對任意長度的時序數據進行處理，但當實際應用中的時間間隔較大時，RNN可能會出現梯度爆炸或梯度消失等結果導致建模失敗[12]。

1.2 GRU神經網絡

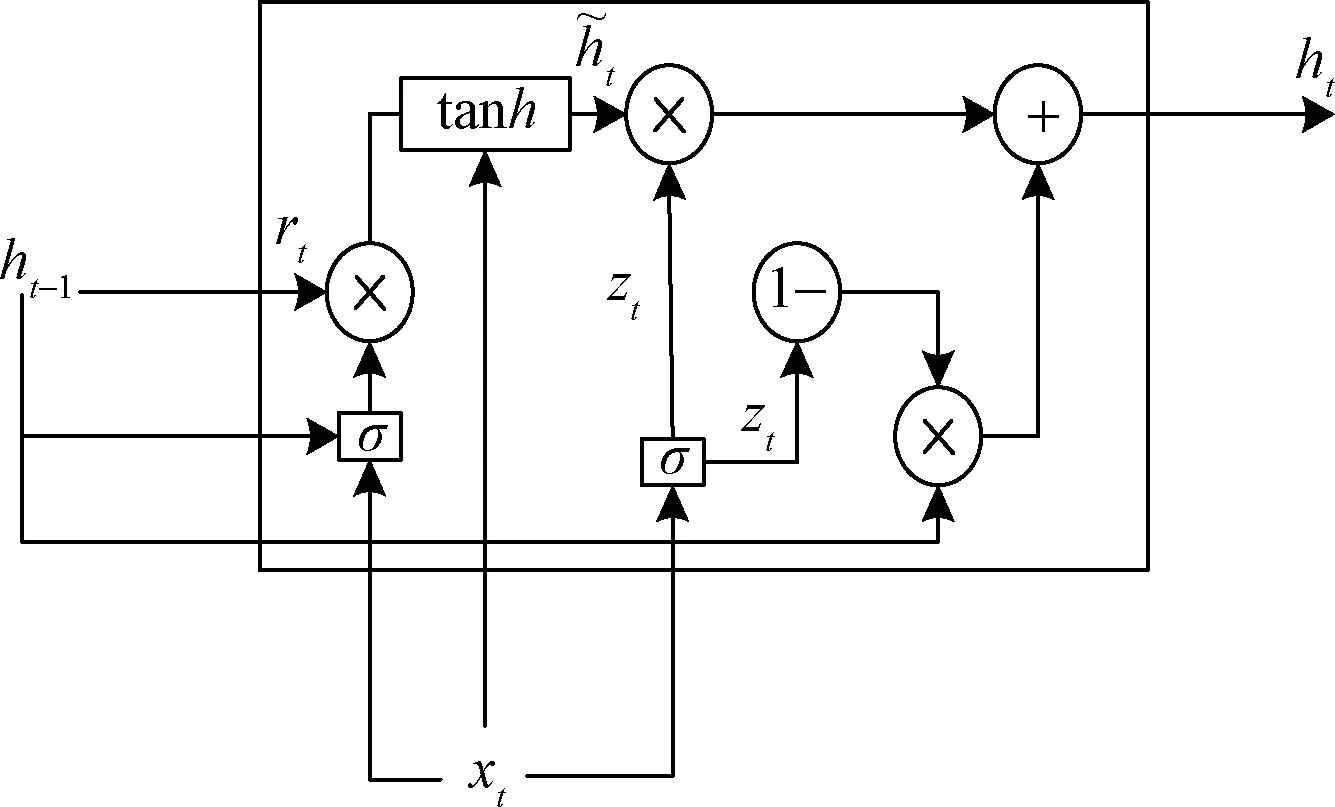
圖2 GRU循環單元結構Fig.2 GRU recurrent unit structure

GRU網絡神經元通過式(3)～式(6)更新狀態。

rt=σ(Urxt+Wrht-1+br)

(3)

zt=σ(Uzxt+Wzht-1+bz)

(4)

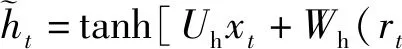
(5)

(6)

式中：σ為sigmoid函數；○表示兩個矩陣相應元素的乘積。rt為重置門；Ur和Wr為重置門的權重矩陣；br為重置門的偏置矩陣；zt為更新門；Uz和Wz為更新門的權重矩陣；bz為更新門的偏置矩陣；bh為隱含層的偏置。

由式(3)～式(6)可知，當rt=1、zt=0時，GRU神經網絡即為傳統的循環神經網絡。

在處理實際問題時，當前時刻的狀態可能不只與歷史信息相關，未來的信息也會對其產生一定影響，只考慮單向信息會影響網絡模型的預測性能。雙向GRU神經網絡[8,14](bidirectional gated recurrent unit,BGRU)由兩層信息傳遞方向不同的循環網絡組成，即在原GRU網絡基礎上增加一個按時間逆序傳遞信息的網絡層，充分利用輸入序列的上下文信息。按時間展開的BGRU神經網絡結構如圖3所示，其使用兩個隱含層來提取過去和未來的信息，兩個隱含層連接到同一輸出層，當前狀態的最終輸出如式(7)所示。

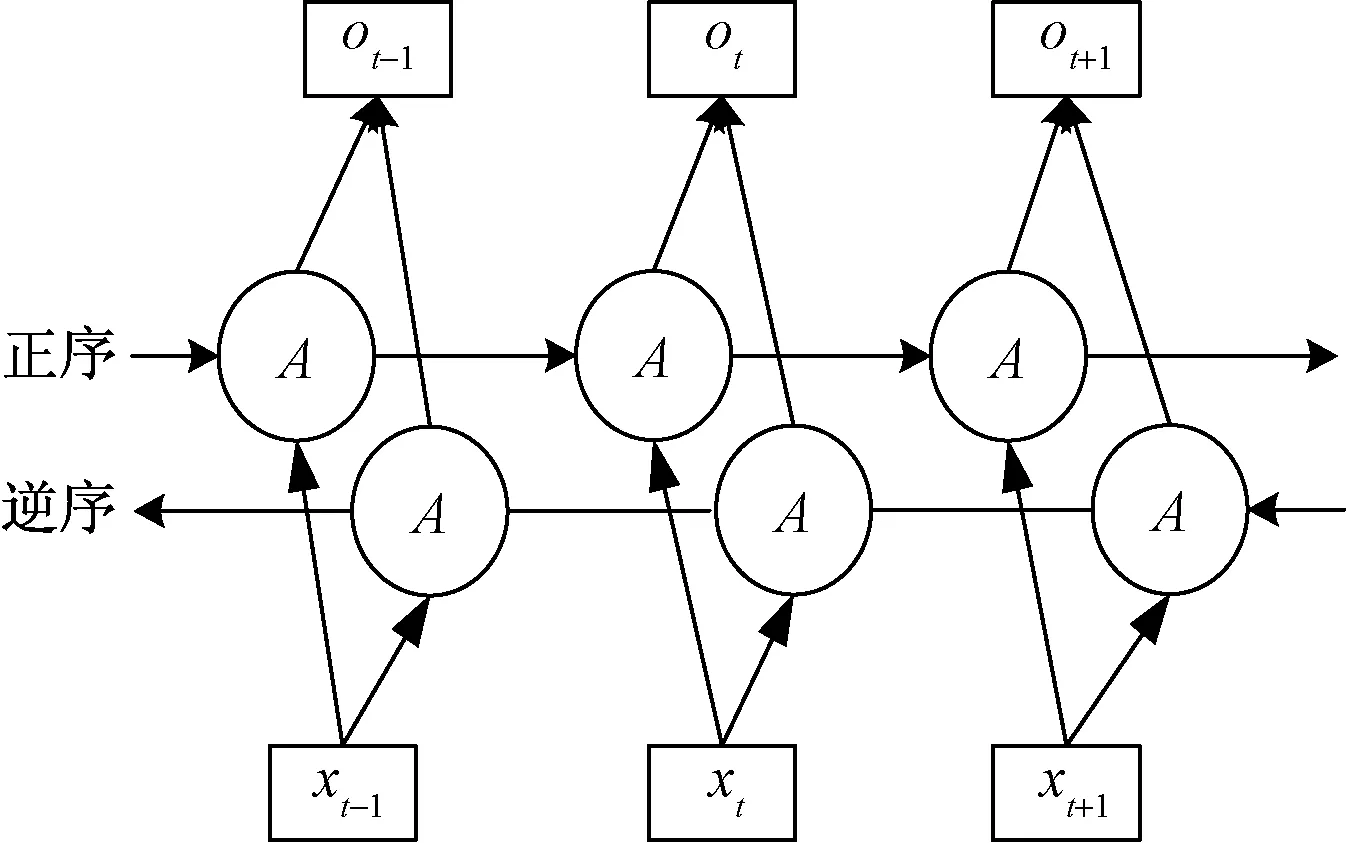
圖3 按時間展開的BGRU神經網絡結構Fig.3 BGRU structure expanded by time

(7)

2 變量選取與數據處理

2.1 輔助變量選取

以某1 000 MW超超臨界火電機組為研究對象，從現場分散控制系統(distributed control system,DCS)數據庫中按采樣周期為1 min選取正常工作時連續的2 500組歷史運行數據進行仿真實驗。

考慮到汽輪機熱耗率的影響因素眾多，為提高預測模型的訓練速度與精度，建模時應選取與熱耗率關聯度更高的因素。汽輪機熱耗率的計算公式為

HR=3 600[Dmshms+Dhrhhr-Dcrhcr-Dfwhfw-

Dshhsh-Drhhrh]/Pe

(8)

式(8)中:HR為汽輪機熱耗率；Dms為主蒸汽流量；hms為主蒸汽焓值；Dhr為再熱器出口蒸汽流量；hhr為再熱器出口焓值；Dcr為再熱器入口蒸汽流量；hcr為再熱器入口焓值；Dfw為鍋爐給水流量；hfw為鍋爐給水焓值；Dsh為過熱蒸汽減溫水流量；hsh為過熱蒸汽減溫水焓值；Drh為再熱蒸汽減溫水流量；hrh為再熱蒸汽減溫水焓值；Pe為機組發電負荷。

由于該機組正常運行時過、再熱蒸汽減溫水流量很少，對機組熱耗率影響較小，可忽略不計。此時給水流量近似等于鍋爐主蒸汽流量，再熱器入口蒸汽流量近似等于再熱器出口蒸汽流量。因此可將式(8)簡化為式(9)：

HR=3 600[Dms(hms-hfw)+Drh(hhr-hcr)]/Pe

(9)

主蒸汽和再熱器入口、出口蒸汽的焓值均可由相應的壓力和溫度表示，鍋爐給水焓值也可采用其壓力和溫度來表示[4,15]。部分參數之間具有較強的相關性，選作輸入變量對模型精度影響不大，反而會增加模型的訓練時間。因此，結合式(9)最終選取表1所示的9個變量作為模型的輸入變量，汽輪機熱耗率為模型輸出變量[16]。

表1 模型的輸入與輸出變量Table 1 Input and output variables of the model

2.2 數據預處理

SG(Savitzky-Golay)濾波器是一種廣泛應用于數據平滑降噪的低通濾波器，通過最小二乘卷積實現局部區間的多項式擬合，能夠有效去除數據的高頻噪聲。該方法有兩個關鍵的參數：滑動窗寬N和多項式擬合階數k。若N太長，會導致有效信號丟失；若N太短，則會影響降噪性能。k過高時可能會致使新噪聲出現；k過低時則可能會導致信號失真。因此，應合理選取N和k的取值以實現隨機降噪和保持有效信號的平衡[17]。SG濾波器實現數據降噪的基本原理如式(10)所示:

(10)

式(10)中:S為原始信號；s*為降噪后的信號；Ci為第i次的降噪系數；N為(2m+1)組數據的滑動窗寬；j為數據樣本集中的第j個樣本。

現場DCS中獲取的數據樣本往往具有較大的噪聲，故采用SG濾波器對原始數據進行降噪處理。經過多次實驗確定：SG濾波器的滑動窗寬N取31，多項式擬合階數k取3。以汽輪機熱耗率為例，其采用SG濾波器降噪的結果如圖4所示。由圖4可以看出，處理后數據的異常值明顯減少，降噪效果顯著。

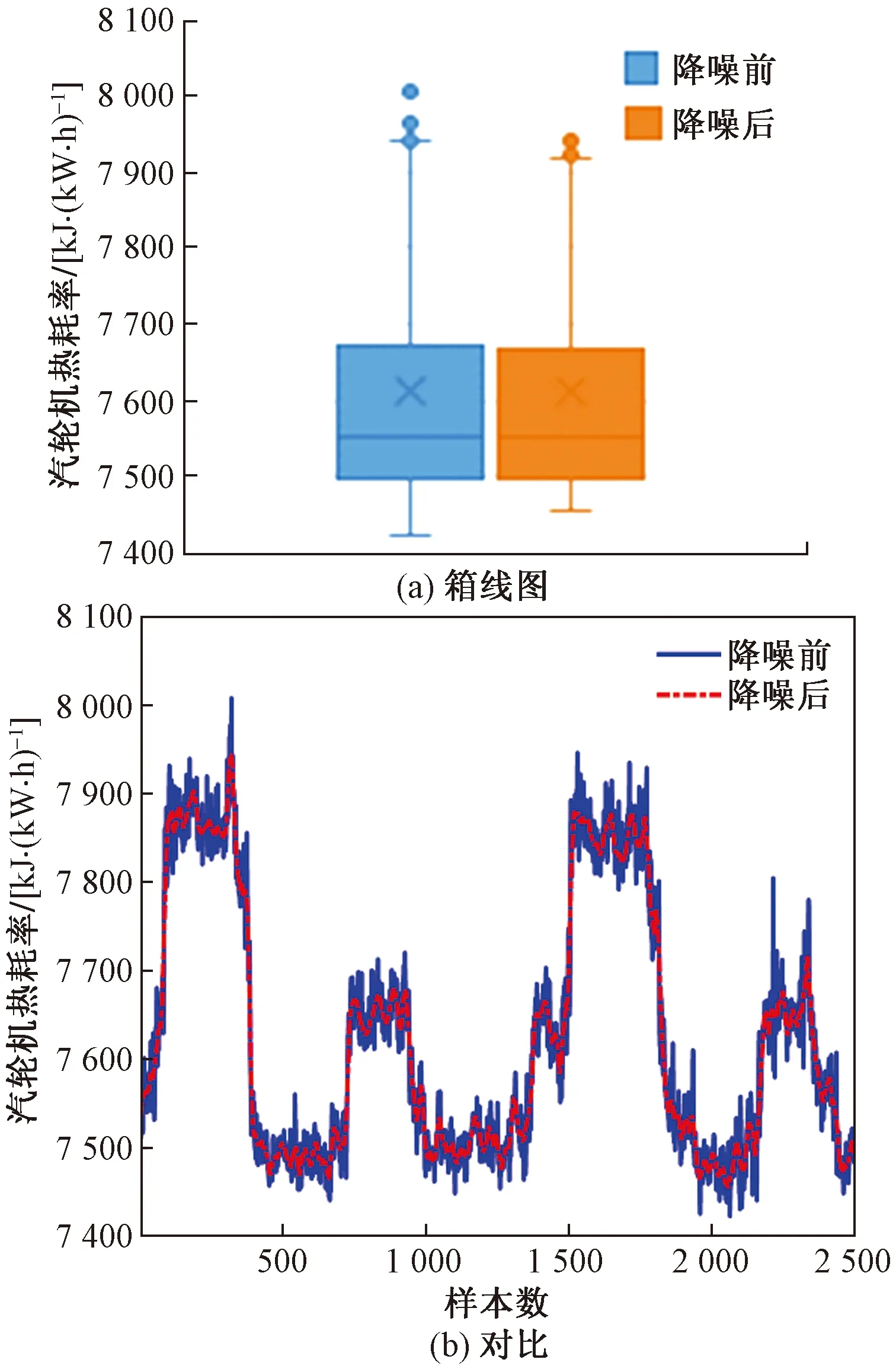
圖4 汽輪機熱耗率降噪結果Fig.4 Noise reduction results of steam turbine heat rate

3 汽輪機熱耗預測模型

3.1 建模與驗證

采用Windows 10系統下的Python語言進行編程，通過人工神經網絡開發庫Pytorch實現BGRU網絡模型的搭建。模型優化方法采用Adam算法[18]；損失函數選用均方誤差(MSE)；非線性激活函數選用ReLU函數；初始學習率取0.01；訓練次數為2 000次。采用dropout機制避免過擬合現象，其值設置為0.2。由表1可知，BGRU神經網絡模型的輸入和輸出節點的個數分別為9和1。經過多次實驗，隱藏單元設置2個GRU層，每層取12個節點。

為防止模型訓練時各變量因量綱不同而影響模型的精度和泛化能力，在建模前先對數據樣本進行標準化處理，轉換為[0,1]的數。將標準化后的2 500組數據中的前2 000組作為訓練樣本建立BGRU神經網絡汽輪機熱耗率預測模型，并與傳統RNN預測模型作對比。兩種模型的預測結果及相對誤差曲線如圖5所示。由圖5可以看出，兩種神經網絡模型的預測值都能以較高的精度逼近真實值，BGRU的誤差曲線波動范圍更小。

圖5 模型預測結果及相對誤差曲線Fig.5 Model prediction results and relative error curves

為測試BGRU神經網絡熱耗率預測模型的泛化能力，采用剩余500組樣本數據作為測試集，將該模型的預測結果與BP神經網絡、傳統RNN等預測模型進行對比分析，得到測試集的預測結果如圖6所示。由圖6可以看出，與其他2種算法相比，BGRU神經網絡汽輪機熱耗率預測模型能夠更好地跟蹤熱耗率真實值的變化趨勢，泛化能力更強。

圖6 模型測試結果對比Fig.6 Model test result comparison

為進一步分析BGRU神經網絡預測模型的預測精度與泛化能力，采用平均相對誤差(MAPE)、平均絕對誤差(MAE)以及相關系數(R2)等作為評價指標對3種模型測試集的預測結果進行評價，評價結果記錄如表2所示。

由表2可知，針對測試集，BGRU神經網絡熱耗率模型預測結果的各項指標均比其他2種預測模型更好。其中，相關系數更是高達0.941 9。綜上所述，BGRU模型的泛化能力更強、預測精度更高。

表2 3種模型的測試集性能對比Table 2 Comparison of performance of 3 models

3.2 魯棒性分析

汽輪機熱耗率預測模型應該具有較高的魯棒性，即當輸入變量發生小幅度隨機擾動時，預測模型應該依然能夠保持一定的預測精度[5]。因此，采用在輸入變量原始數據上增加擾動的方法測試BGRU神經網絡汽輪機熱耗率預測模型的魯棒性。

給測試樣本集的主蒸汽流量和給水溫度分別附加5%的擾動量，預測模型的相對誤差曲線如圖7所示。

圖7 模型預測相對誤差曲線Fig.7 Model prediction relative error curves

由圖7可知，主蒸汽流量和給水溫度分別附加5%的擾動后，BGRU神經網絡預測模型的計算值仍然能夠以較高的精度跟蹤真實值的變化。兩組擾動實驗的預測相對誤差均在±2%以內，主蒸汽流量擾動對預測模型的影響更大。因此，小幅度擾動對BGRU神經網絡模型的影響較小，該模型具有較強的魯棒性。

4 結論

(1) 建立了基于雙向GRU神經網絡的汽輪機熱耗率預測模型，該模型的建立為汽輪機組的運行經濟性優化奠定了基礎。

(2) 采用Savitzky-Golay濾波器對所選輸入、輸出變量的現場真實數據進行降噪處理，降噪后的數據異常值明顯減少。

(3) 利用處理后的數據建立汽輪機熱耗率預測模型，并與BP神經網絡及傳統循環神經網絡等不同算法建立的預測模型進行對比，驗證了雙向GRU網絡模型的建模精度與泛化能力。

(4) 在主蒸汽流量和給水溫度兩個變量原始數據的基礎上分別附加5%的擾動量進行測試，表明雙向GRU神經網絡熱耗率預測模型對擾動具有良好的魯棒性。