NPLS技術在高超聲速邊界層轉捩研究中的應用

易仕和, 劉小林, 陸小革, 牛海波, 徐席旺

(國防科技大學 空天科學學院, 長沙 410073)

0 引 言

近年來，由于高超聲速飛行器研制的需要，高超聲速空氣動力學相關問題受到了極大的關注。基于流動顯示與精細測量技術對高超聲速流場進行研究，能夠清晰直觀地反映出流場結構，對理解流動機理和解釋流動現象具有重大意義。然而高超聲速條件下，流場具有非定常、可壓縮和強梯度等特點，這對流動顯示與精細測量技術提出了巨大的挑戰。

前期相關的高超聲速流動顯示研究基本都采用紋影和陰影等光學方法進行測量。早在1965年，Potter[1]等就開始嘗試用陰影技術，對高超聲速流場進行可視化研究。后來Demetriades[2]等同樣采用陰影技術，對馬赫數8條件下的圓錐邊界層進行了流動顯示研究。從陰影圖像中能夠大致分辨出流場中的渦結構，并以此判斷邊界層發生轉捩的位置。近年來Laurence及其研究團隊通過高速紋影實驗對高超聲速邊界層轉捩問題開展了一系列的研究[3-8]，通過將流動顯示結果和壁面脈動壓力結果以及邊界層穩定性計算結果進行對比，驗證了紋影流動顯示技術在邊界層擾動波研究中的適用性。采用陰影紋影等光學方法對高超聲速流動問題進行研究，其最大優點是作為非接觸式測量方法，對流場沒有干擾，但是具有共同的缺點，即受到光路積分效應的影響，空間分辨率低，而且風洞壁面邊界層等無關區域帶來的干擾始終存在。

以濾波瑞利散射(Filtered Rayleigh Scattering，FRS)技術為代表的流場激光層析成像，很好地避免了上述紋影和陰影等方法帶來的時間和空間積分效應的影響。普林斯頓大學Mark Huntley[9]等用CO2增強型濾波瑞利散射技術對馬赫數8條件下的尖橢錐進行了邊界層轉捩相關研究。第一次發現了邊界層的轉捩是從中心軸上小尺度渦結構的出現開始的，而不是從外側的橫流區域開始的。德克薩斯農工大的Humble[10]等同樣基于冷凝瑞利散射流動顯示技術研究了馬赫數4.9條件下凸曲面對高超聲速邊界層的影響，分析了不同壓力梯度條件下的邊界層發展規律。

本文作者基于自主研發的NPLS技術，在超聲速復雜流場精細結構測量方面開展了大量工作[11-19]。NPLS技術以名義粒徑15nm的納米粒子作為示蹤物質，相比傳統PIV技術中用的微米級示蹤粒子而言，納米粒子的動力學特性更好地滿足粒子跟隨性要求[20]。近年來，研究團隊成功將NPLS測試技術運用到高超聲速流場的流動顯示與精細測量研究中[21-25]，在《高超聲速邊界層流動穩定性實驗研究》[25]一文中，側重分析了高超聲速邊界層流動穩定性相關實驗結果，研究了高超聲速裙錐邊界層中的第二模態波和三角翼邊界層中的橫流不穩定性。作者在本文則重點介紹NPLS技術在高超聲速邊界層轉捩研究中的典型應用，展示了在靜音風洞噴管邊界層流態測量、直圓錐邊界層以及三角翼邊界層轉捩測量等方面得到的典型NPLS結果。

1 風洞與測試技術

1.1 高超聲速靜音風洞

風洞自由來流中的噪聲大部分來源于噴管壁面邊界層產生的聲輻射擾動。對于常規風洞，其噴管壁面邊界層通常為湍流狀態，湍流邊界層中復雜的渦系結構會產生大量聲輻射擾動，因此常規風洞噪聲水平高。國防科技大學空氣動力學實驗室高超聲速靜音風洞(如圖1所示)，通過在噴管喉道附近設計相應的抽吸裝置來控制邊界層狀態。當抽吸閥門打開時，噴管內邊界層流動狀態從常規的湍流狀態變為層流狀態，從而大大降低了自由來流的噪聲水平。該靜音風洞的噪聲水平約千分之一[25-26]，明顯低于常規風洞的噪聲水平。

圖1 高超聲速靜音風洞組成及靜音噴管圖Fig.1 Schematic diagram of hypersonic quiet wind tunnel and the quiet nozzle

1.2 NPLS流動顯示與精細測量技術

NPLS系統組成如圖2所示。該測試技術具有高時空分辨率，高信噪比的優點，NPLS技術的詳細原理和適用性可參見文獻[13]。

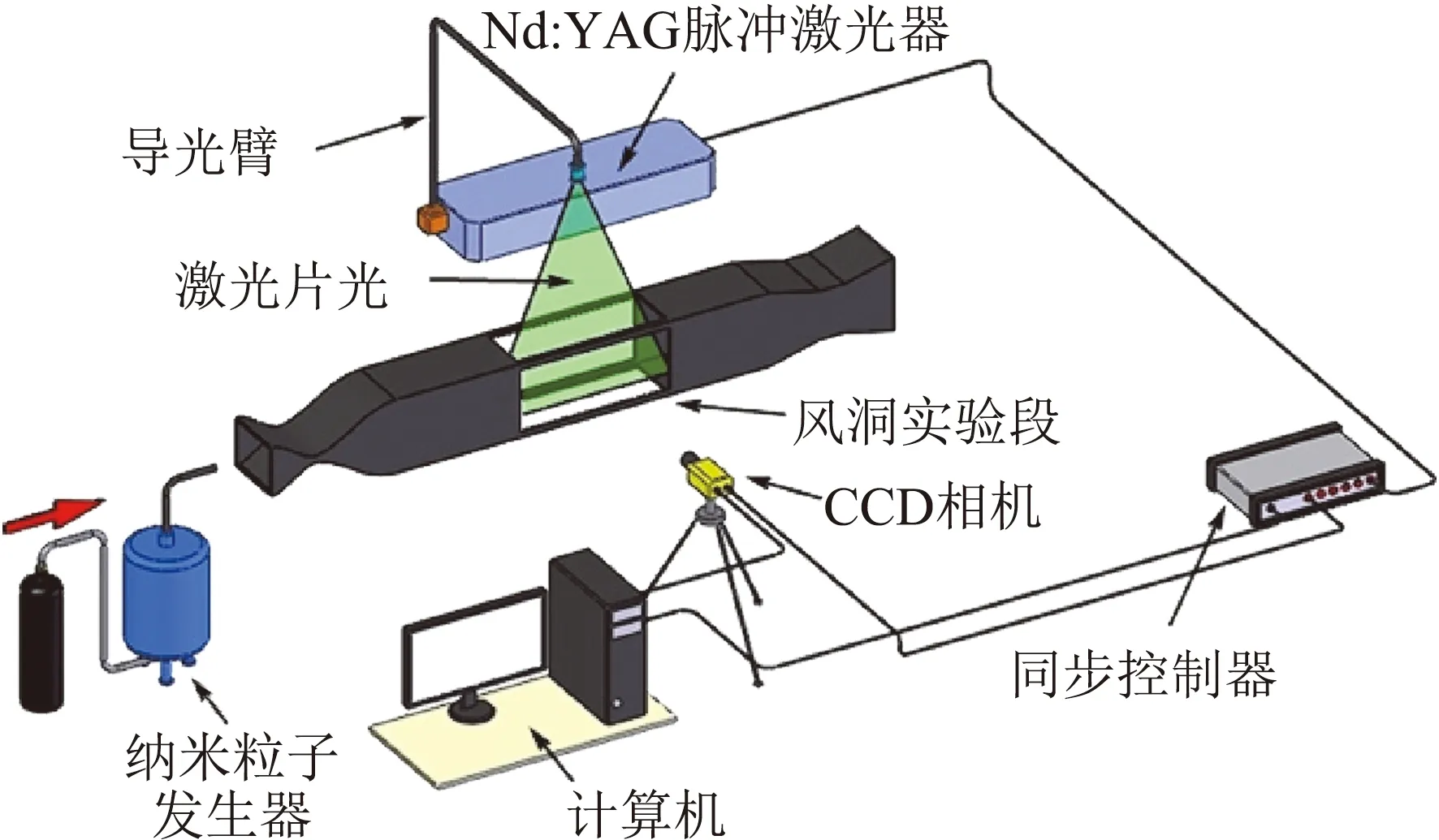
圖2 NPLS系統組成Fig.2 Schematic diagram of NPLS system

2 高超聲速靜音風洞噴管邊界層流態測量

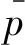
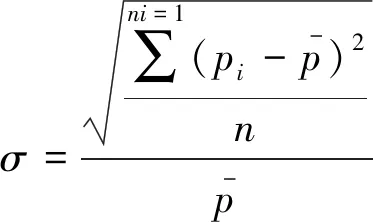
(1)

風洞噪聲水平測量是高超聲速靜音風洞流場校測的核心工作之一。圖3所示為高超聲速靜音風洞噪聲水平測量示意圖，采用Kulite XCE-62高頻壓力傳感器對皮托壓力脈動進行測量，傳感器固有頻率為300 kHz。在高超聲速靜音風洞的初期調試過程中，需要不斷調節噴管喉道抽吸縫大小，并對每個抽吸狀態下的風洞噪聲水平進行測量，從而找到最佳靜音流場對應的抽吸縫位置。在高超聲速條件下，噴管中氣流速度快，受到高溫高壓氣流沖刷，微小固體顆粒狀雜質可能直接打壞用于噪聲水平測量的高頻傳感器，從而大大增加了實驗成本和實驗周期。

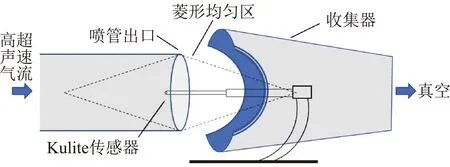
圖3 高超聲速靜音風洞噪聲水平測量示意圖Fig.3 Schematic diagram of turbulence noise level measurement in hypersonic quiet wind tunnel

NPLS技術通過對高超聲速靜音風洞噴管邊界層的流態進行測量，能夠有效應用到高超聲速靜音風洞的流場校測中。常規高超聲速噴管邊界層是湍流邊界層，靜音噴管的邊界層要求是層流邊界層。而通過NPLS技術可以測量得到的噴管出口射流剪切層NPLS圖像，如果是層流的射流剪切層，則說明噴管出口是層流邊界層；如果是湍流的射流剪切層，則說明噴管出口是湍流邊界層。通過噴管邊界層是層流狀態還是湍流狀態就可以確定高超聲速噴管是否運行在靜音狀態。

圖4所示為高超聲速靜音風洞噴管出口射流剪切層NPLS圖像的典型結果，其中圖4(a)噴管出口射流剪切層為層流剪切層，對應的噴管邊界層為層流邊界層，此時風洞處于靜音運行模式。圖4(b)噴管出口射流剪切層為湍流剪切層，對應的噴管邊界層為湍流邊界層，此時風洞處于噪聲運行模式。按照圖3所示方式，采用Kulite 高頻壓力傳感器對靜音噴管來流的皮托壓力脈動進行測量，傳感器脈動電壓輸出隨時間的變化曲線如圖5所示。由圖可見，當邊界層抽吸閥打開時，靜音噴管運行在靜音狀態；邊界層抽吸閥關閉時，靜音噴管運行在噪音狀態。按照式(1)即可得到自由來流的噪聲水平σ。靜音狀態和噪音狀態下，風洞自由來流的噪聲水平σ分別為0.1%和2%。由此數據也可以看出，當風洞邊界層從層流發展為湍流狀態后，邊界層中渦結構產生的聲輻擾動大大增加，導致自由來流中的噪聲水平同樣大幅度增加。在高超聲速靜音流場測量過程中，可以基于NPLS技術對不同抽吸條件下的噴管邊界層進行流動顯示研究，然后選取其中的典型狀態進行脈動壓力測試，這樣減少脈動壓力測量試驗的車次從而大大降低了傳感器被打壞的風險。而且通過噴管邊界層流態的NPLS圖像與脈動壓力傳感器噪聲測量結果的比較，很好驗證噴管邊界層流態與噴管流場噪聲的對應關系。

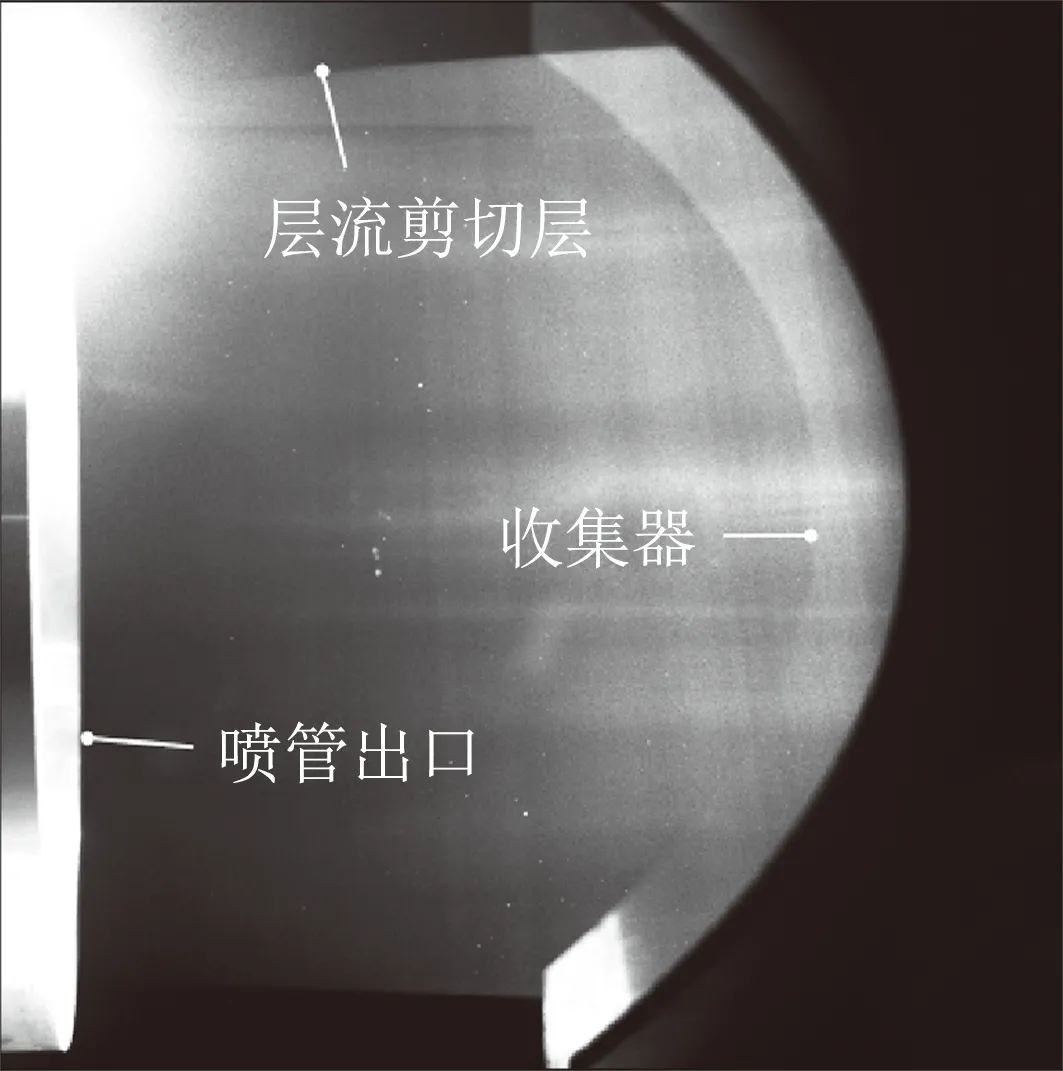
(a) 層流剪切層，抽吸閥打開

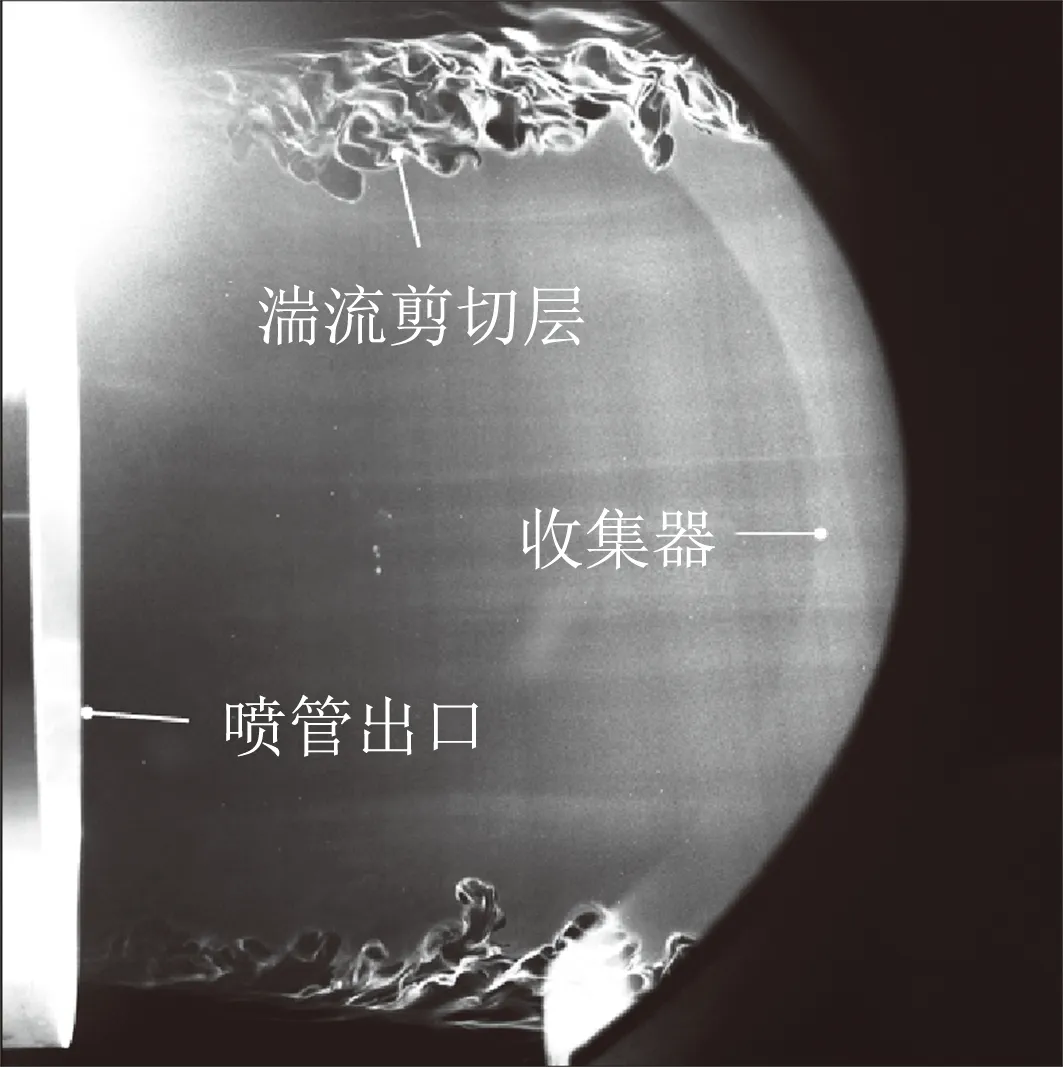
(b) 湍流剪切層，抽吸閥關閉圖4 噴管出口射流剪切層流態NPLS結果Fig.4 NPLS results of the shear layer at nozzle outlet

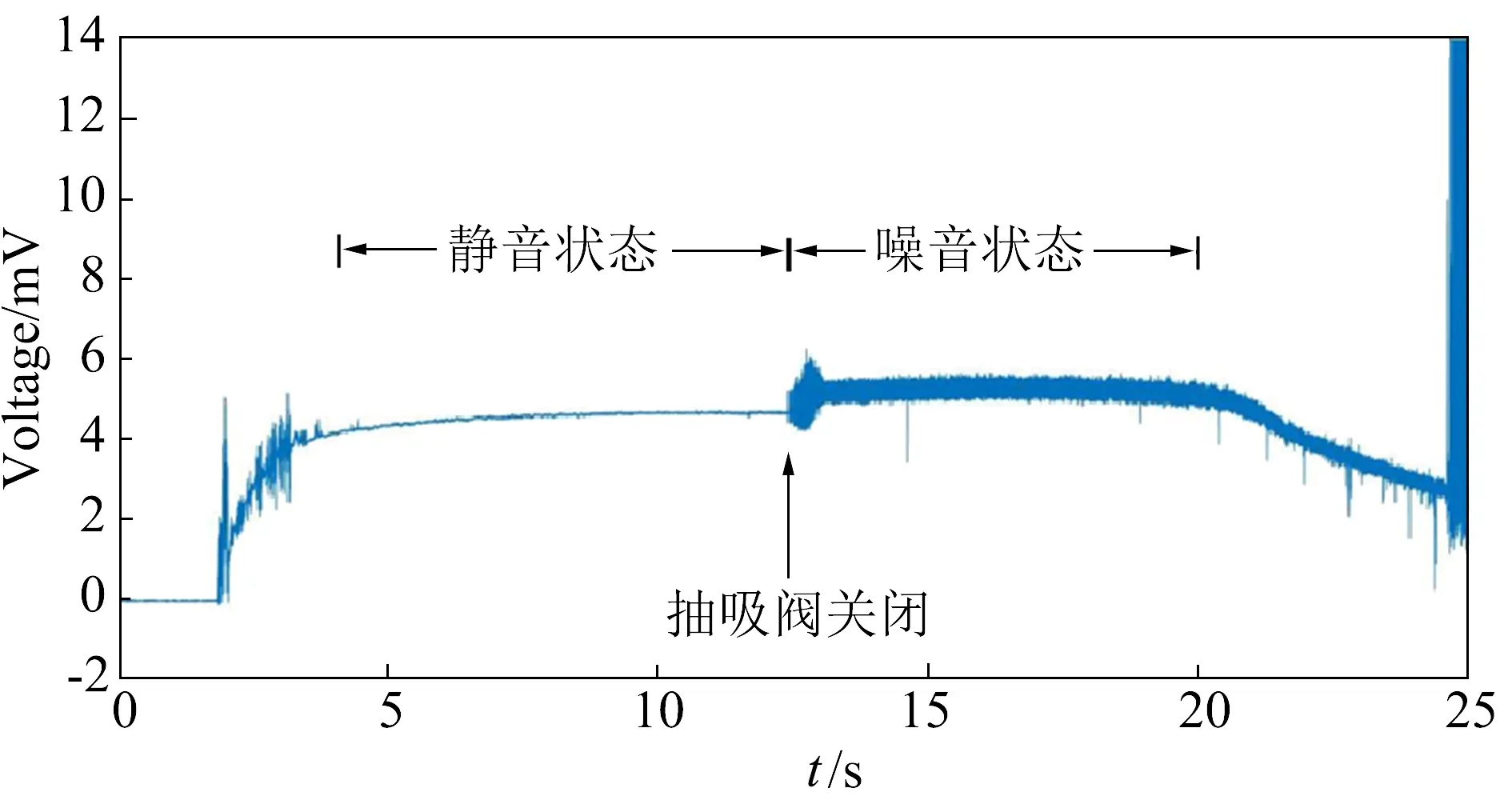
圖5 靜音噴管來流皮托壓力的傳感器脈動電壓輸出曲線Fig.5 Voltage curve measured by the pitot pressure sensor in the quiet nozzle

3 高超聲速圓錐邊界層轉捩研究

3.1 高超聲速圓錐邊界層研究

基于NPLS技術對不同迎角條件下高超聲速圓錐邊界層轉捩進行研究。實驗模型為半錐角5°的光滑直尖錐，模型總長度600 mm。圖6給出了5°光滑尖錐流向平面流動精細結構測量的實驗布局示意圖。模型迎角α狀態分別為0°、2°、5°，流場單位雷諾數Re=1.0×107m-1，測量結果均為模型的迎風面。

圖7為模型0°迎角的NPLS圖像，流動方向為從左到右，測量范圍為x=340～580 mm，圖像空間分辨率為35.1 μm/pixel，CCD相機跨幀時間設置為10 μs。從圖7中可以觀測到光滑尖錐邊界層發展過程，在x=340～430 mm之間可看到規則的第二模態繩狀波結構(見圖7中局部放大結構)，在x=430～500 mm之間邊界層發展進入轉捩區，在x=500 mm之后可以看到明顯的大尺度渦結構，尖錐邊界層完全發展為湍流。

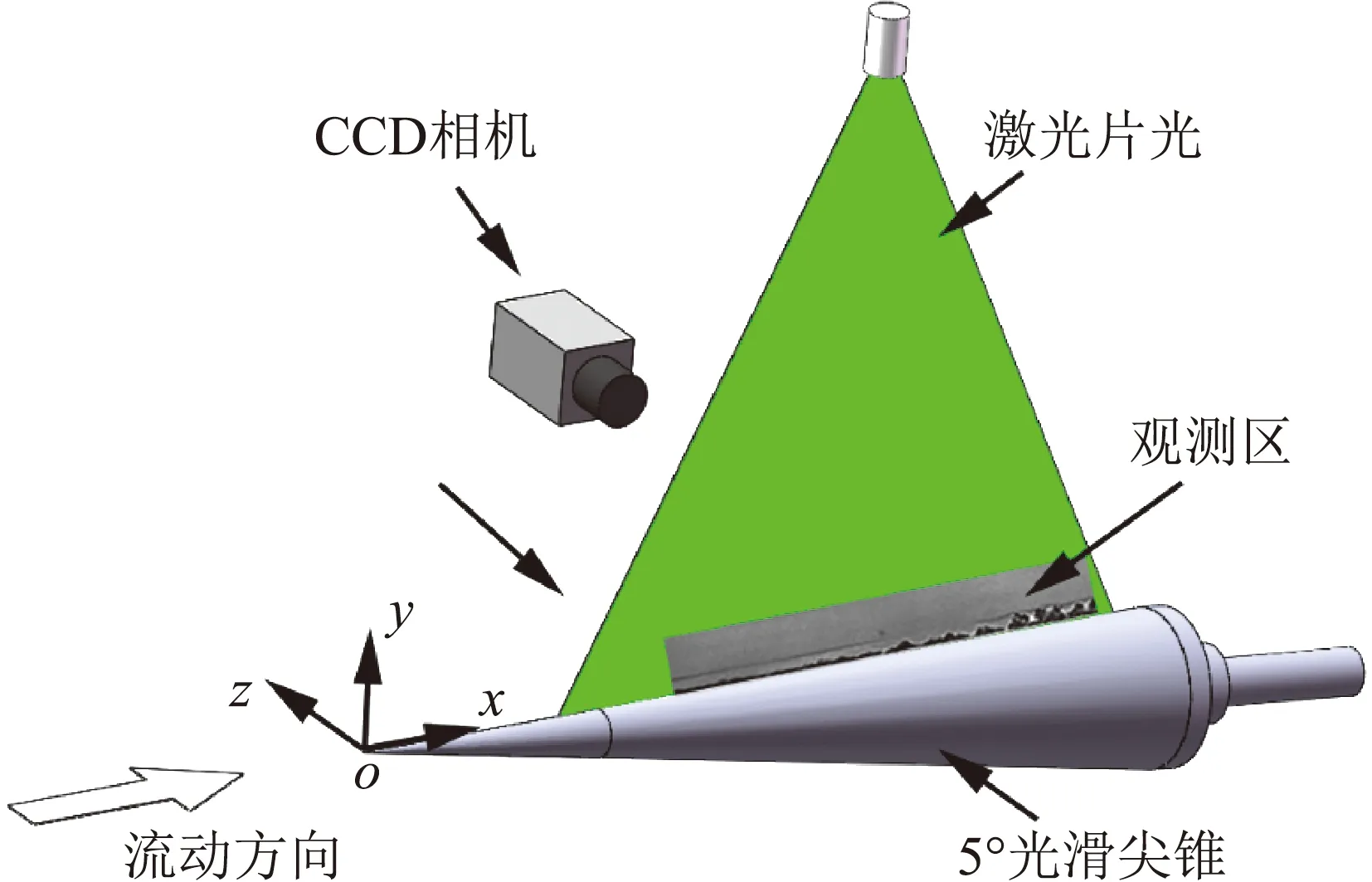
圖6 5°光滑尖錐NPLS拍攝示意圖Fig.6 Schematic Diagram of 5° half angle cone

根據圖7中的時間相關結果，取繩狀波結構計算得到Δt=10 μs時間內渦結構沿流向位移為7.47 mm，計算得到渦結構沿流向位移速度約為747 m/s，此速度小于風洞運行時的主流速度。根據圖中規則繩狀波結構計算得到第二模態波的統計波長為5.39 mm，計算得到5°光滑尖錐在此工況下的特征頻率為138 kHz。

圖8和圖9分別給出了5°光滑尖錐在2°和5°迎角時的NPLS圖像，從圖中可以看出在相同雷諾數條件下，隨著迎角的增大，尖錐模型的邊界層轉捩位置明顯推遲，并且在迎角增大后，也未觀察到明顯的第二模態波結構。

3.2 臺階對高超聲速圓錐邊界層轉捩的影響規律研究

在高超聲速靜音風洞中基于NPLS技術對帶軸對稱臺階的直圓錐高超聲速邊界層轉捩進行實驗研究。圓錐半錐角為7°，如圖10所示，模型頭部可以更換，分別裝配后可得臺階高度為0.5 mm的前臺階和后臺階。模型頭部具有直徑0.8 mm的小鈍度。為了進一步檢驗NPLS結果的有效性，在該模型上布置了7個高頻壓力測點，具體分布如圖10所示，7個測點坐標分別為：x1=20 mm、x2=80 mm、x3=140 mm、x4=200 mm、x5=260 mm、x6=320 mm、x7=380 mm。

圖7 5°光滑尖錐0°迎角NPLS圖像(Re=1.0×107 m-1，Δt=10 μs)Fig.7 NPLS image of the boundary layer on the 5° half angle cone at 0° angle of attack (Re=1.0×107 m-1，Δt=10 μs)

圖8 5°光滑尖錐2°迎角NPLS圖像(Re=1.0×107 m-1)Fig.8 NPLS image of the boundary layer on the 5° half angle cone at 2° angle of attack (Re=1.0×107 m-1)

圖9 5°光滑尖錐5°迎角NPLS圖像(Re=1.0×107 m-1)Fig.9 NPLS image of the boundary layer on the 5° half angle cone at 5° angle of attack (Re=1.0×107 m-1)

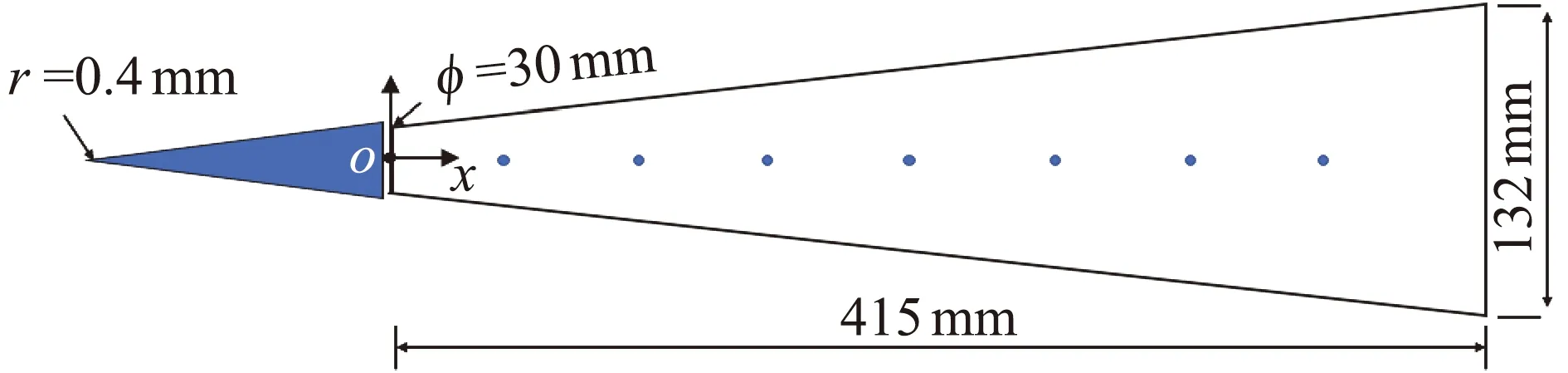
圖10 7°圓錐模型示意圖Fig.10 Schematic Diagram of 7°half angle cone

如圖11所示為單位雷諾數為Re=7×106m-1時，帶0.5 mm高度前/后臺階的小鈍錐的NPLS圖像。其中流動方向為從左至右，流向范圍為225～365 mm，照片的空間分辨率約為77.09 μm/像素。圖中可見，兩種模型中均可觀察到清晰的繩狀第二模態波。后臺階模型中邊界層在x=230～255 mm之間繩狀第二模態波清晰可見，發展至x=260 mm附近第二模態波消失，在x=280 mm后開始變厚并逐漸轉捩為湍流。但在前臺階模型中，邊界層發展至x=320 mm附近仍可見的第二模態波，在x=340 mm后才開始逐漸轉捩為湍流。對比可見，后臺階模型中邊界層發展明顯早于前臺階模型。

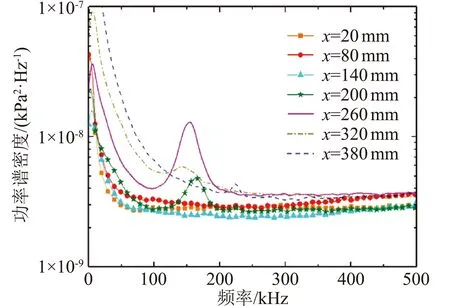
如圖12所示為相同條件下得到的壁面脈動壓力功率譜密度曲線。圖中可見，功率譜密度曲線中出現有特征頻率在140～180 kHz范圍內的第二模態波。

圖11 0.5 mm前/后臺階小鈍錐邊界層NPLS結果(Re=7×106 m-1)Fig.11 NPLS image of the boundary layer on the cone with 0.5 mm forward/backward facing step (Re=7×106 m-1)

在兩種模型中均可見第二模態波在向下游發展的過程中出現有幅值先增大后減小、特征頻率逐漸降低的規律。但將兩種模型結果對比可見，后臺階模型中第二模態波初次出現的測點位置更靠近上游，且后臺階模型中第二模態波消失、邊界層開始呈現為湍流流態的位置也更靠近上游，結果表明后臺階模型中邊界層轉捩明顯早于前臺階模型，該結論與NPLS測量結果一致。

4 高超聲速三角翼邊界層轉捩研究

三角翼流動是典型的非對稱三維流動，對高超聲速條件下三角翼流動進行流動顯示研究有助于深入厘清橫流不穩定性對邊界層轉捩過程的影響規律。圖13是實驗模型示意圖。所用的模型為75°后掠角三角翼，采用平板構型。模型厚度為7 mm，長度為500 mm，寬度為250 mm。模型頭部為R=3.5 mm球頭，兩側前緣半徑也為3.5 mm。選用的實驗狀態為0°迎角，單位雷諾數1.44×107m-1。

圖14是三角平板展向NPLS實驗結果。實驗時，激光片光平行于模型表面，圖14(a)和圖14(b)片光分別距離壁面0.5 mm和2 mm，相機位于模型正上方。圖14(a)中大部分區域為黑色，是由于片光切入了層流邊界層內部。NPLS圖像灰度能夠反映與密度相關的標量場，層流邊界層內流體密度都很小，因此NPLS圖像灰度小，呈現黑色。而從x=150 mm附近，開始出現破碎的亮的結構，顯示此時的邊界層狀態已經由層流變為了湍流，由于湍流結構將主流的高密度氣體卷入底層低密度區，因此可以看到此片光位置處的亮的破碎的邊界層流動結構。觀察圖14(a)中的湍流區域，可以看出，三角翼上，邊界層轉捩至湍流的轉捩陣面呈現出大致的“肺葉狀”分布，靠近三角翼前緣部分轉捩陣面與前緣大致平行，三角翼對稱面位置處轉捩陣面內凹，轉捩較兩側推遲。

(a) 前臺階

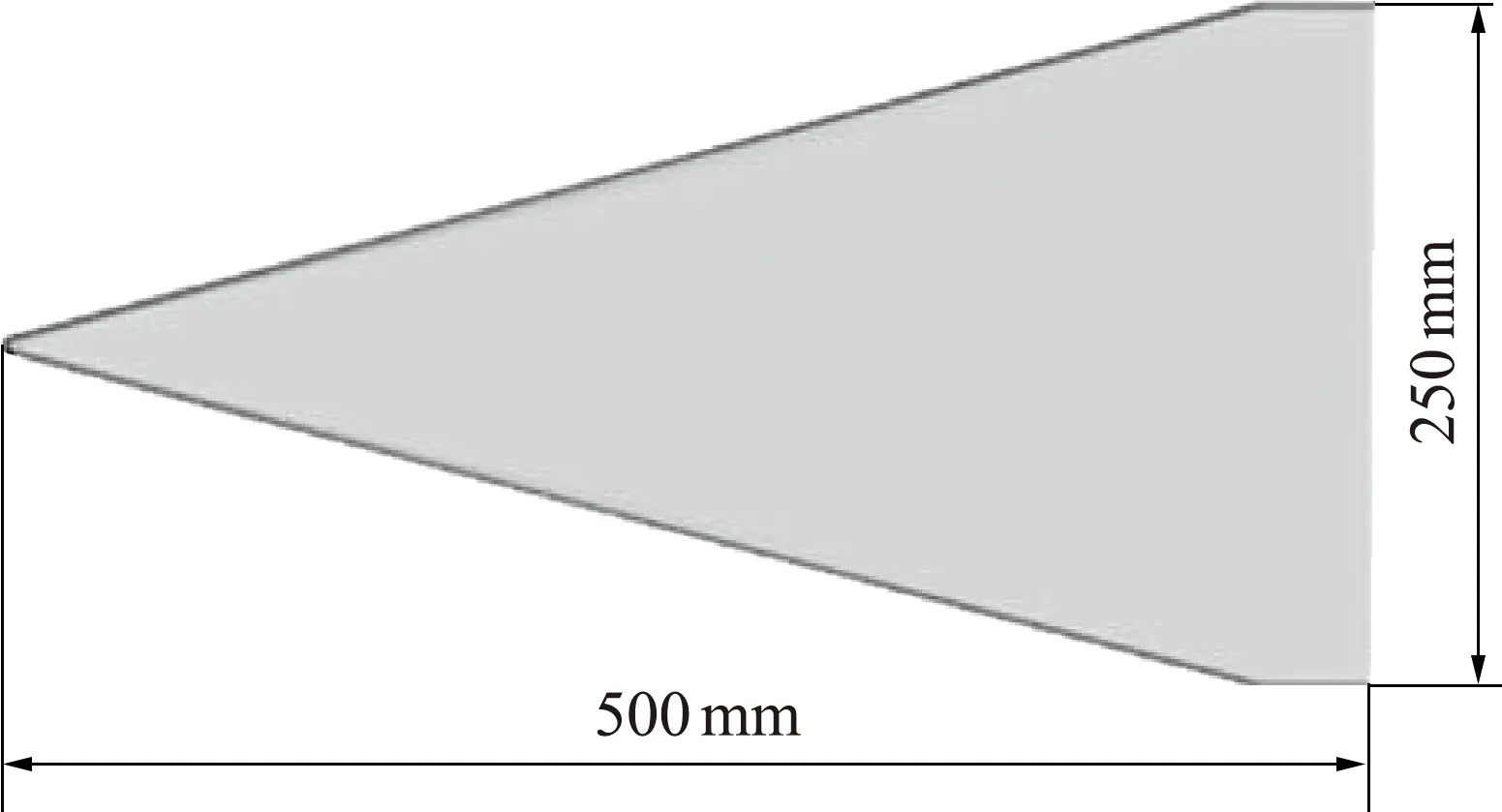
圖13 三角翼模型示意圖Fig.13 Schematic diagram of delta wing

(a) 片光距壁面0.5 mm

(b) 片光距壁面2 mm圖14 三角翼展向NPLS實驗結果 (α=0°,Re=1.44×107 m-1)Fig.14 NPLS results on the spanwise plan over the delta wing (α=0°, Re=1.44×107 m-1)

圖14(b)中片光距離壁面比圖14(a)更遠，片光的大部分區域處于主流中，因此整體亮度比圖14(a)更亮，當邊界層由層流變為湍流時，湍流結構會將底層的低密度流體帶入高層，因此，在x>100 mm位置觀察到的黑色結構為大尺度的湍流結構。靠近頭部的地方有暗區域，原因是頭部處流體擾流，造成此處邊界層厚。在x=100～150 mm范圍內能夠觀察到大尺度的結構，說明此時處于轉捩區，邊界層轉捩不完全。到x>150 mm時，湍流結構尺度變小，更加破碎，說明此時邊界層完全轉捩為湍流，與圖14(a)中出現破碎的湍流結構的區域相對應。

圖15是對應狀態下的溫敏漆(TSP)實驗結果。不同顏色代表了溫度相對于風洞未運行時升高的程度。從x=150 mm位置開始，模型表面溫升明顯增加，說明此時發生了邊界層轉捩。觀察轉捩陣面，可以發現，陣面形狀也呈現“肺葉狀”的分布，靠近三角翼前緣部分的轉捩陣面與前緣平行，靠近中心線區域轉捩位置后凹。

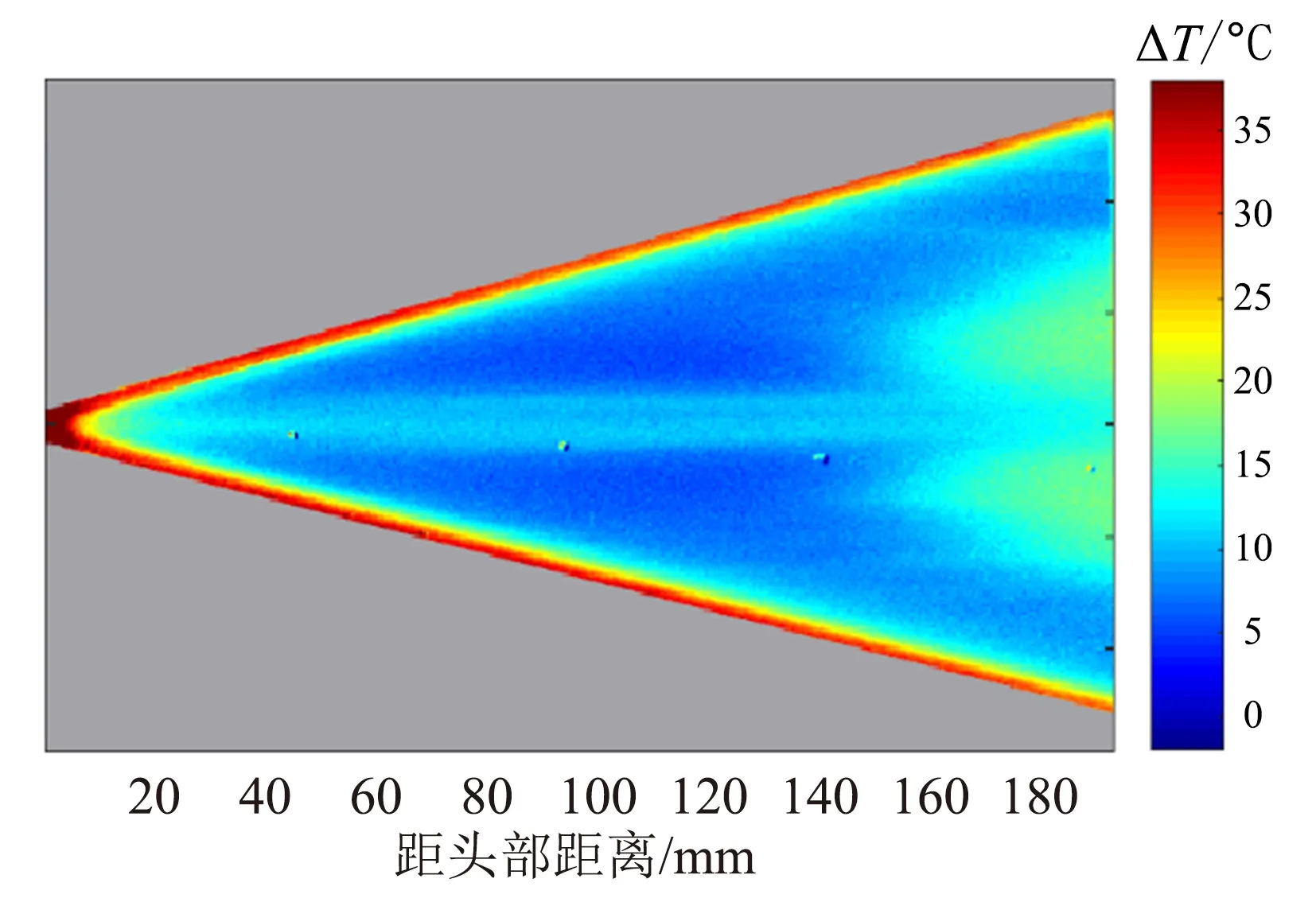
圖15 三角翼表面TSP實驗結果(α=0°, Re=1.44×107 m-1)Fig.15 TSP result on the delta wing (α=0°, Re=1.44×107 m-1)

TSP結果反映的是模型壁面上時間平均的溫度分布,而NPLS結果反映的是處于激光片光平面的瞬態的精細流場結構。將圖15中TSP結果與圖14所示不同高度NPLS結果進行對比，TSP反映出的邊界層轉捩陣面的位置和形狀與圖14(a)中符合較好。圖14(a)中，片光位置距離壁面0.5 mm，NPLS結果顯示的是邊界層底層的流場精細結構，與TSP結果的相符進一步說明了邊界層底層的湍流流動結構是導致模型表面溫升增大的原因。 而圖14(b)中，片光位置距壁面2 mm，此處的流動不會對模型表面產生直接影響，因此所反映的規律與TSP有些許差異。

5 結 論

本文主要介紹了NPLS技術在高超聲速邊界層轉捩研究中的典型應用。在高超聲速靜音風洞噴管邊界層流態測量中，基于噴管出口射流剪切層NPLS照片，可以確定對應的噴管邊界層流態，從而判斷風洞自由來流噪聲水平，大大降低了靜音風洞調試成本，并很好驗證噴管邊界層流態與噴管流場噪聲的對應關系。在高超聲速圓錐邊界層研究中，NPLS技術能夠清晰測量到邊界層中的繩狀第二模態波等精細流動結構，并且基于NPLS結果，可以分析迎角和臺階等因素對邊界層轉捩的影響規律。在三角翼流動研究中，通過展向NPLS結果，可以清晰地觀察到破碎的湍流結構，得到“肺葉狀”的轉捩陣面。NPLS結果與基于高頻脈動壓力及溫敏漆等技術得到的結果一致，證明了NPLS技術應用于高超聲速邊界層轉捩測量的有效性與準確性。