單點懸浮系統的自抗擾控制算法

楊 杰，石 恒，胡海林，黃 晨

(江西理工大學 電氣工程與自動化學院， 江西 贛州 341000)

磁懸浮可以用于實現各種機械結構的高速、無摩擦運轉，比如運用到高速磁浮列車、高速磁懸浮電機、磁懸浮軸承等[1]。單點懸浮系統是一個非常典型的非線性系統，并且是磁浮列車懸浮控制的基礎，盡管在較長時期里有過諸多智能控制算法在單點懸浮系統的控制中的技術嘗試，但是在工程實踐中，由于難以實現磁浮列車受到軌道不平順、乘客上下車和在車廂走動的影響而引起的磁浮間隙隨機性的即時跟蹤，最終此類算法均表現得不盡人意。目前磁浮列車基本上還是依靠PID控制算法實施行駛控制。

1999年韓京清教授提出了具有抗干擾且不依賴被控對象模型的“自抗擾控制”[2](ADRC,Auto Disturbance Rejection Control)，經過近20年的發展，ADRC算法已經在坦克炮控系統、導彈姿態控制、機器人控制等系統中廣泛運用。

本文針對單點懸浮系統的動力學特性，將ADRC算法應用于磁浮控制，并與PID進行比較，從中探索出適用于磁浮列車行駛控制的技術特點。

1 系統模型與問題描述

1.1 單點懸浮系統模型

本文以常導磁吸式(EMS)磁浮列車為例，參見圖1(a)所示。

為了保證這種懸浮的可靠性和列車運行的平穩性，使直線電機具有較高的功率，必須精確地控制電磁鐵中的電流，使磁場保持穩定的強度和懸浮力，使車體與導軌之間保持大約10 cm的間隙。EMS通常采用氣隙傳感器來實施系統的間隙反饋控制。

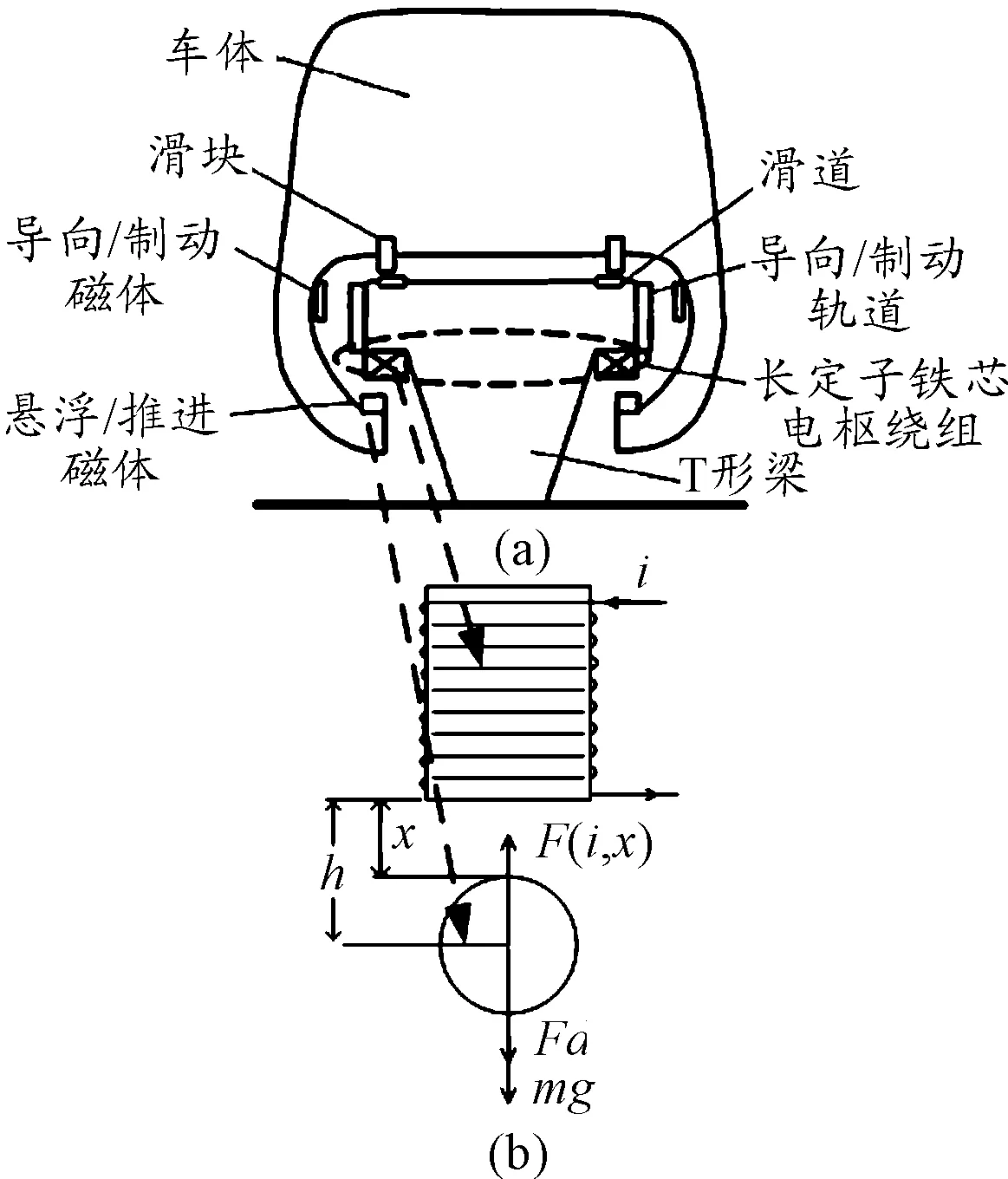
圖1 EMS系統原理及其基礎動力學模型

為了引入“自抗擾控制”算法，有必要對實際的懸浮系統進行一種抽象與簡化，因此可以獲得如圖1(b)所示的單點懸浮基礎動力學模型，該動力學模型即表達了單點懸浮物理系統。圖中的虛線(箭頭與圓框)系抽象(虛擬)過程的“思維表達線”。

圖1(b)中的上方為固定電磁鐵，代表設置于軌道的長定子鐵心電磁鐵，下方的鐵磁性球，代表列車模擬體。當電磁鐵上的線圈繞組通入電流i時產生的電磁場對下方的鐵磁性球便形成吸力F(i,h)。當產生的吸力與鐵磁性球的重力相等時，鐵磁性球就懸浮在空中，兩者之間的間隙x即是列車的懸浮高度。此時，鐵磁性球處于不穩定的平衡狀態，當鐵磁性球受到外力fd干擾時，極易失去平衡。為了使系統維持穩定，勢必需要加上反饋環節。為此，必須設計一種控制算法，以確保懸浮達到穩定控制的技術要求。

當列車達到設定的懸浮高度時，電磁吸力和列車重力相等，此時列車就被懸浮起來。可見，單點懸浮系統的控制等價于磁浮列車整車懸浮的控制基礎。其動力學方程為

(1)

式中:m為鐵磁性球的質量；h為鐵磁性球的質心到電磁鐵磁極面的距離,h=x+d,d為鐵磁性球的半徑，x亦即鐵磁性球的懸浮高度；g為地球重力加速度；fd為鐵磁性球所受的外界干擾力；F即F(i,h)，為鐵磁性球所受到的吸力。其中

(2)

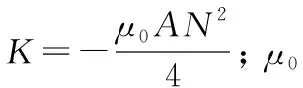
(3)

忽略懸浮鐵磁性球位置的變化對電感的影響，可以得到方程

(4)

式中：U為電磁鐵兩端電壓；R為電磁鐵等效電阻；L為電磁鐵繞組等效電感。

當鐵磁性球處于平衡狀態時，重力和電磁吸力相等，由牛頓第二定律可得鐵磁性球此時所受的合力為零。即

mg+F(i0,h0)=0

(5)

F(i0,h0)為鐵磁性球懸浮高度為x0、平衡電流為i0時電磁鐵對鐵磁性球的電磁吸力。

聯立式(3)、式(4)、式(5)后，得

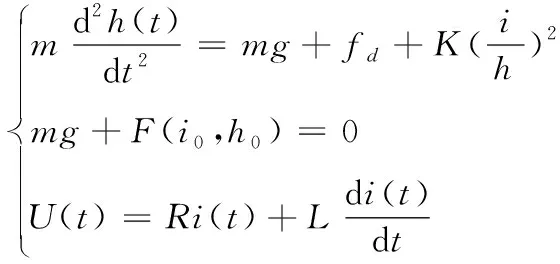
(6)

即為單點懸浮系統運動動力學方程。

1.2 單點懸浮系統模型線性化

對于單點懸浮系統，電磁鐵的電流作為控制輸入量，并不考慮感抗對于系統的影響時，可在平衡點x0附近對動力學方程進行線性化處理。

對式(2)進行泰勒級數展開并省略高階項[3]

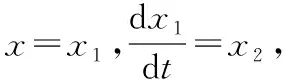
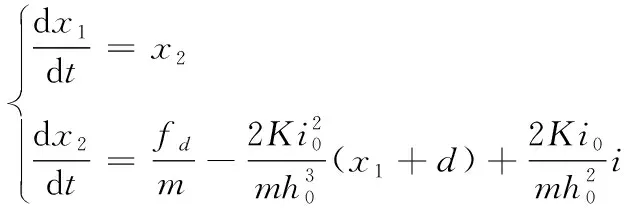
(7)

2 自抗擾控制器的設計

ADRC主要由跟蹤-微分器(TD)、擴張狀態觀測器(ESO)、非線性狀態誤差反饋控制律(NLSEF)組成，用TD安排過渡過程并提取給定輸入的微分信號；用ESO估計對象狀態和不確定擾動作用[4]；用過渡過程與狀態估計間的誤差的非線性組合和擾動估計量的補償來生成控制信號[5]。ADRC實現的核心在于ESO中的擾動補償項，該項對系統的模型參數變化和未知外擾作用共同給予估計和補償[6]。

本文設計的單點懸浮系統的ADRC結構如圖2所示。

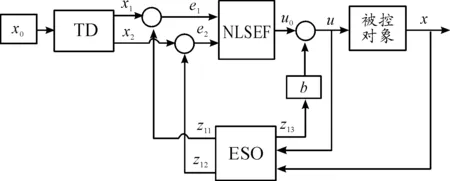
圖2 單點懸浮系統自抗擾控制結構框圖

單點懸浮系統需要考慮變化的設定懸浮間隙，并以此判斷控制器對于變化的設定懸浮間隙的適應性。為了能快速的跟蹤設定懸浮間隙的變化，并且避免因為設定值的突變所造成控制量的劇變而產生超調[6]，將ADRC控制器中的TD環節，設計為二階Levant微分器[7]，其二階滑膜微分器的表達式為

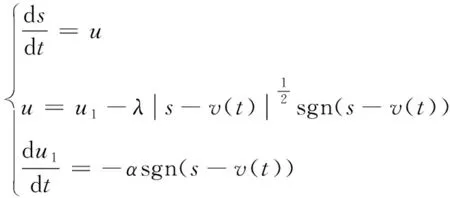
(8)

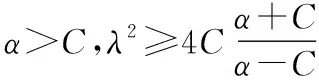
三階擴張狀態觀測器為

(9)

式中，βi>0(i=1,2,3)，飽和函數fal(e,α,δ)的作用就是為了抑制信號的抖振，其表達式為

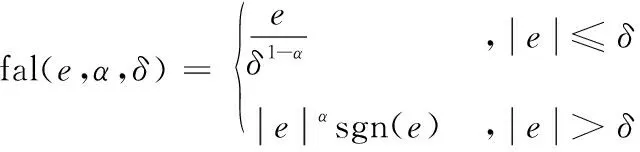
(10)

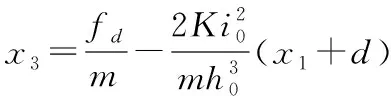
本研究采用的非線性控制律為一種PD形式的非線性控制律，其表達式為：

u=β10fal(e1,α10,δ0)+

β20fal(e2,α20,δ0)

(11)

式中：0<α10<1<α20；e1是設定的懸浮位置信號與懸浮小球實際的懸浮位置之差；e2是設定懸浮位置信號微分與懸浮小球速度輸出之差；fal(e,α,δ)函數同式(10)表達式相同。

通過擴張狀態觀測器的變量z13跟蹤被控對象中擴張出的未知干擾狀態變量x3[8]通過消減x3(即z13)可將原被控對象簡化為

(12)

這就變成了一個雙重積分器串聯單位增益的控制問題，由式(7)、式(12)可得控制量

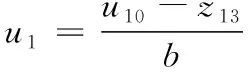
(13)

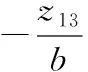
3 參數整定

4 仿真分析

單點懸浮系統的仿真參數如表1所示。

對單點懸浮系統分別采用PID和ADRC控制方式，主要在以下幾個方面展開仿真研究：

1) 在系統突然加大負載情況下的冗余能力；

2) 控制器對設定間隙變化的適應性；

3) 控制器對設定參數變化的魯棒性。

表1 單點懸浮系統仿真參數

1) 階躍響應

在圖3中，實線為ADRC間隙H階躍響應曲線，虛線為PID控制的間隙H階躍響應曲線。由圖3可以看出ADRC的動態性能優于PID，ADRC的調節時間為0.085 s，PID控制的調節時間為0.35 s；ADRC超調量小于PID控制的超調量；由此可以看出在單點懸浮系統的間隙階躍響應中ADRC的性能優于經典的PID控制。

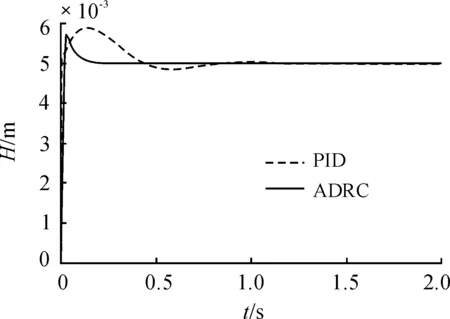
圖3 ADRC和PID間隙階躍響應曲線

如圖4所示，從上到下的順序，實線是階躍響應中ADRC擴張狀態觀測器對輸出信號x、微分信號y、干擾信號z的觀測輸出曲線；虛線是單點懸浮系統中實際的懸浮高度輸出、微分信號輸出和實際干擾信號的輸出曲線，可知ADRC的擴張狀態觀測器可以很好的觀測到系統的輸出信號、微分信號和干擾信號。

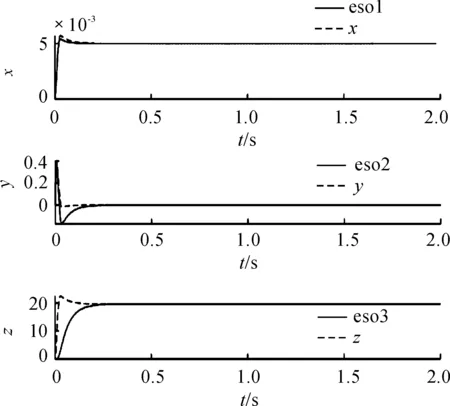
圖4 階躍響應ADRC的擴張狀態觀測器輸出曲線

2) 冗余實驗

圖5中實線和虛線分別表示采用ADRC和PID控制方法時，在5 s時刻突然加4.7 N階躍負載的間隙H響應曲線。ADRC和PID兩種控制方法在此種情形下最大間隙變化量分別為1.954 mm和2.245 mm：完全恢復到平衡位置ADRC需要0.3 s的時間，PID控制需要1.3 s的時間。此處所加的負載是單點懸浮小球自身質量的5.1倍，由此可知ADRC比PID更能適應大范圍負載的變化，ADRC閉環控制系統具有很強冗余能力和抗干擾能力，這也為高速磁懸浮列車搭接結構的冗余控制提供了一條技術思路。

圖5 ADRC和PID冗余實驗曲線

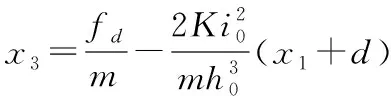
正是由于ADRC控制器中擴張狀態觀測器的這樣一種特殊的性質使得ADRC具有很強的抗干擾能力和天然的解耦性能，給控制不確定對象系統克服其復雜的擾動性提供了解決方案[10]。

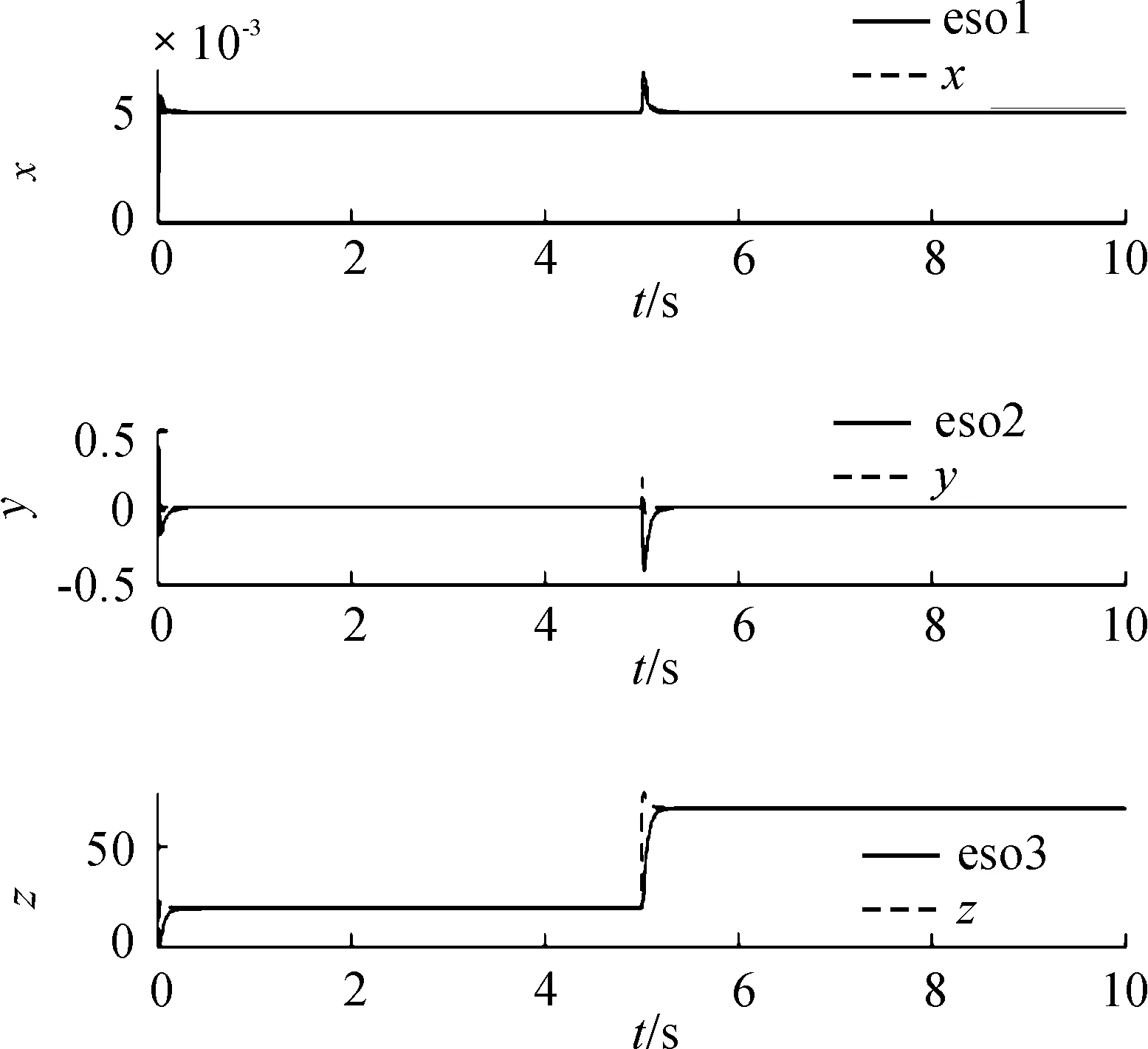
圖6 冗余實驗ADRC的擴張狀態觀測器輸出曲線

3) 跟隨性試驗

圖7中短虛線為設定的間隙H變化曲線，變化范圍在3～9 mm，實線和長虛線分別為ADRC和PID控制輸出間隙曲線，可知，ADRC比PID控制能更好地跟蹤變化的設定間隙。

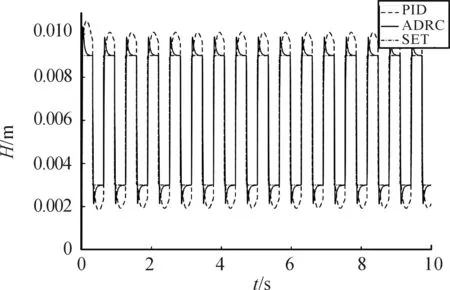
圖7 ADRC和PID跟隨性試驗輸出曲線

圖8中在設定間隙不斷變化的情況下，ADRC的擴張狀態觀測器在觀測輸出信號x、微分信號y和干擾信號z方面依然展現出很好的觀測性能。

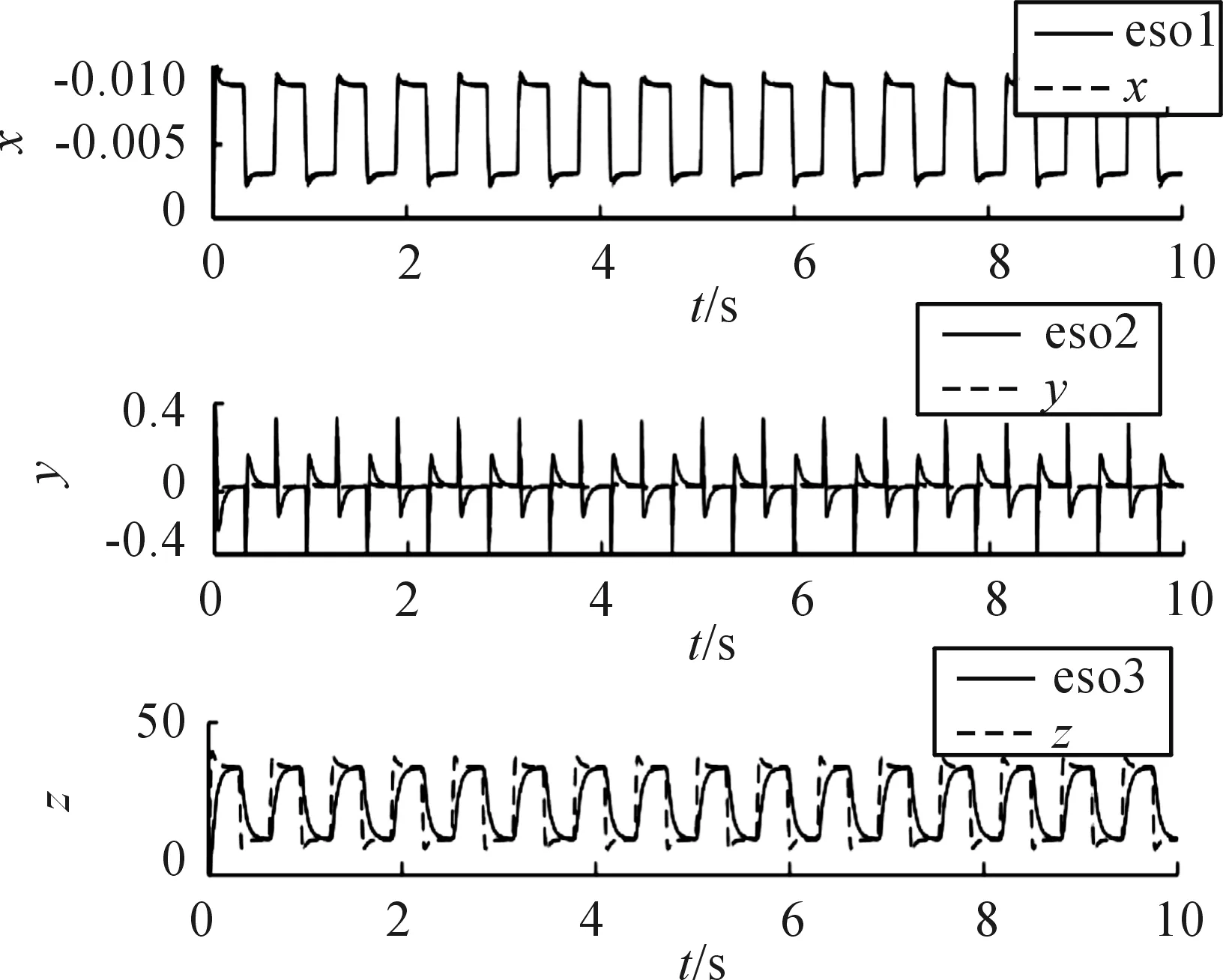
圖8 跟隨性試驗中ADRC擴張狀態觀測器輸出曲線

5 結論

ADRC充分發揮了非線性函數的強功能和高效率，通過Levant微分器在基本無超調的前提下實現信號的快速跟蹤，從而解決超調與快速性的矛盾；非線性PD控制律中fal函數中的參數一般取值范圍為0<α<1,0<δ≤1，結合公式(10)fal函數的表達式易得該函數實際上蘊含了“小誤差大增益，大誤差小增益”的控制知識和具有快速收斂的特性，因此這種控制律易于實現，并且具有良好的魯棒性和適應性。

單點懸浮系統仿真結果表明ADRC在快速性、適應性和克服大擾動能力方面都明顯優于經典的PID。

單點懸浮系統的ADRC仿真實驗可以為工程實現提供理論指導，對于具體的工程化運用，參數必須結合實際系統的具體特性來調整，才能取得滿意的控制效果。