擺彈機構運動特性與誤差分析

彭京徽，張弘弨，朱孝磊，王世哲

(1.海軍工程大學 a.兵器工程學院； b.電氣工程學院, 武漢 430033； 2.海軍研究院, 北京 100073)

大口徑艦炮供彈系統主要完成運彈、揚彈、擺彈、轉彈、輸彈和退彈六個動作，擺彈機作為自動供彈系統的重要組成部分，將揚彈末端垂直擺放的彈藥快速、準確地擺送至轉彈機工作位置。進行擺彈機運動特性研究與誤差分析對改進自動機設計，提高機構可靠性對提升裝備性能有著重要意義。

國內已有學者對滿足現代化海戰要求的含擺彈機構的艦炮自動供彈系統展開了研究[1-12]。在常見的擺彈機構研究中，普遍基于有限元法和虛擬樣機技術。文獻[6-7]采用笛卡爾坐標分量和弧坐標分量來共同描述柔性擺彈臂的彈性變形及運動關系。文獻[9]中考慮擺彈臂的柔性變形及參數的隨機分布，以有限元模型為基礎，綜合運用支持向量回歸機與蒙特卡洛法分析動作可靠性。文獻[10]中建立了考慮彈藥質量、質心位置等為隨即變量的擺彈機構數學模型。唐文獻[13]應用ANSYS軟件的FE-SAFE疲勞分析模塊，探討了零件表面粗糙度對中腹擺彈臂的疲勞壽命及安全系數的影響。李淵明[14]運用含間隙機構的分析方法，對擺彈機構進行了運動學和動力學特性分析，并以此對機構的關鍵部件進行了靜力分析和結構改進。

在以上研究的基礎上，本研究基于ADAMS虛擬樣機技術，研究了轉動副不同間隙大小、擺臂柔性、擺彈過程中彈體滑移以及彈藥質量偏差對擺彈運動特性的影響并分析其誤差的成因。

1 擺彈機簡化模型與工作機理

擺彈機構主要由動力原件、齒輪齒條組件、擺彈臂3部分組成(如圖1所示)，其中齒輪軸受支承轉動約束。擺彈機構在豎直位置時抱彈裝置抱住揚彈末端的彈藥，動力源對齒條施加拉力，齒條開始向后運動，嚙合齒輪逆時針轉動并帶動擺彈臂擺動，使得擺彈臂上的彈藥運動到轉彈機交接位置，擺彈過程如圖2所示。

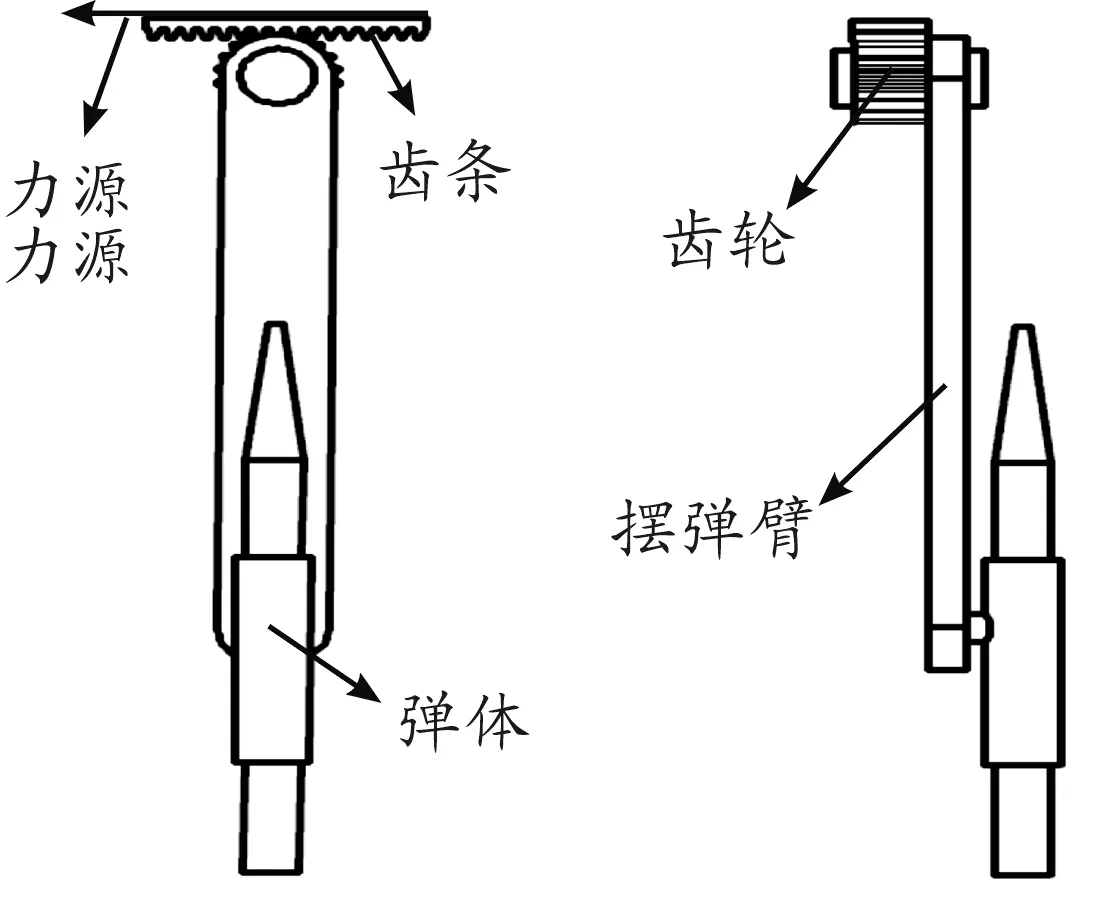
圖1 擺彈機結構

圖2 擺彈運動過程

2 擺彈機構的力學模型

擺彈機擺動過程的受力模型如圖3所示，其中O、Ob、Od分別是齒輪轉軸軸心、擺臂與抱彈裝置的質心、彈體質心；Gb、Gd表示質心Ob、Od處的重力；Lb、Ld是質心Ob、Od到齒輪軸心O的垂直距離；θ表示擺彈臂的轉角；rp是齒輪的分度圓半徑；F是驅動力，與轉角θ關聯。

圖3 擺彈機受力模型

彈體在擺彈運動過程中受力如圖4所示，其中FN是重力作用下抱彈裝置給的支撐力；Fj是抱彈裝置給彈體的緊箍力。

圖4 彈體受力示意圖

3 擺彈機構擺彈運動仿真分析

3.1 轉動副間隙對擺彈運動的影響

兩個相對運動構件動配合時普遍存在間隙，間隙的存在會增加系統的自由度，導致機構運動精度降低和惡化運動穩定性。在擺彈機構中齒輪軸與支承的轉動副間存在間隙，如圖5所示，研究間隙的存在和間隙大小對擺彈運動的影響是研究擺彈機運動的重要內容。

圖5 含間隙轉動副示意圖

在不考慮潤滑條件下，分析含間隙轉動副的碰撞與摩擦常用的接觸力模型[15]是法向非線性滯后阻尼單側接觸力模型與切向Coulomb摩擦力模型[16]。

法相接觸力：

(1)

切向摩擦力：

Ft=-μFNsgn(vt)

(2)

式中：K和D分別為等效接觸剛度和阻尼系數；n為非線性指數，金屬材料通常取1.5；μ為摩擦因數；νt相對切向速度；FN為支撐力。

通過SolidWorks三維建模后將模型導入Adams，對各部件施加相應約束，在不同間隙值δ=0.1 mm、δ=0.3 mm和δ=0.5 mm時分別對齒輪軸與支承間創建接觸力，利用Adams和Matlab聯合仿真分析得到不同大小間隙存在時的擺彈轉角與時間的關系曲線，如圖6所示。

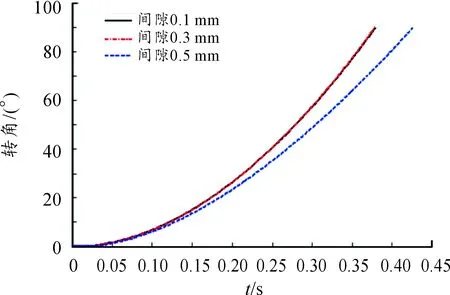
圖6 不同間隙時轉角與時間的關系曲線

由圖6可知，在轉動副間隙值為δ=0.1 mm、δ=0.3 mm和δ=0.5 mm時分別對應的擺彈截止時間t為0.379 2 s、0.378 6 s和0.426 3 s，間隙造成擺彈過程產生誤差，間隙的大小與控制是減小擺彈誤差的方法。

3.2 擺臂柔性對擺彈運動的影響

在擺彈過程中擺彈臂會產生彈性變形，研究擺臂柔性對擺彈運動的影響，有利于提高擺彈動作的可靠性。利用ANSYS對擺彈臂進行柔化處理，如圖7所示，生成mnf中性文件，導入Adams建立剛柔耦合模型進行仿真分析，仿真結果如圖8所示。

圖7 擺彈臂柔化處理示意圖

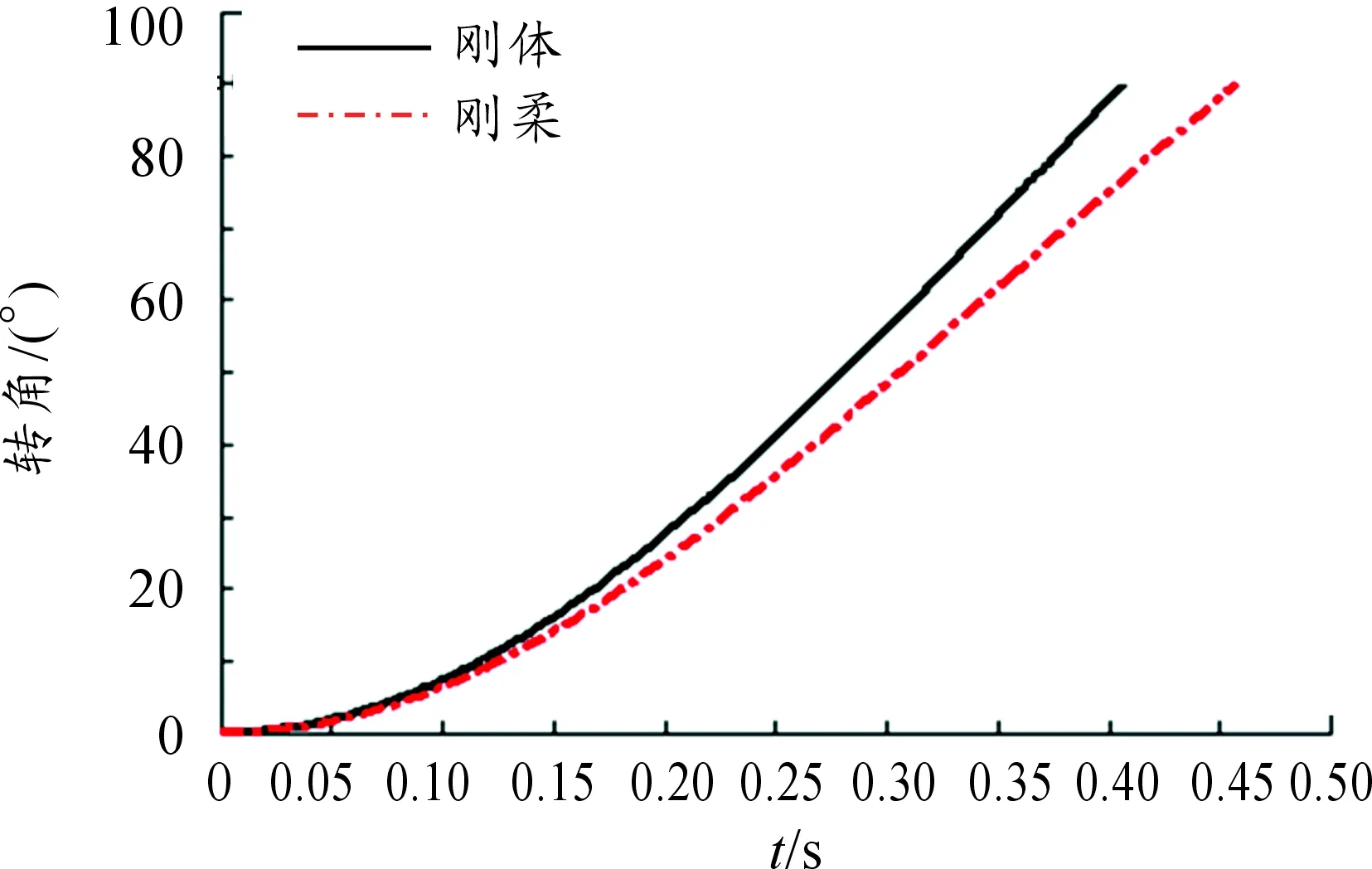
圖8 剛體/剛柔時轉角與時間的關系曲線

由圖8可知剛體模型擺彈截止時間是t=0.406 5 s剛柔耦合模型截止時間是t=0.457 8 s，擺桿柔性會造成擺彈運動時間延長，柔性擺臂仿真時考慮了彈性變形，在機構設計時應當考慮擺臂柔性帶來的影響。

3.3 彈體滑移對擺彈運動的影響

揚彈末端彈體位置會導致擺彈的初始質心偏差，在擺彈過程中彈體也會產生滑移，研究彈體滑移對機構運動特性的影響對提高擺彈機構可靠性與防止掉彈有著重要的意義。對彈體分別施加離心方向0.1m/s2和0.2m/s2的加速度，仿真得到的結果如圖9所示。

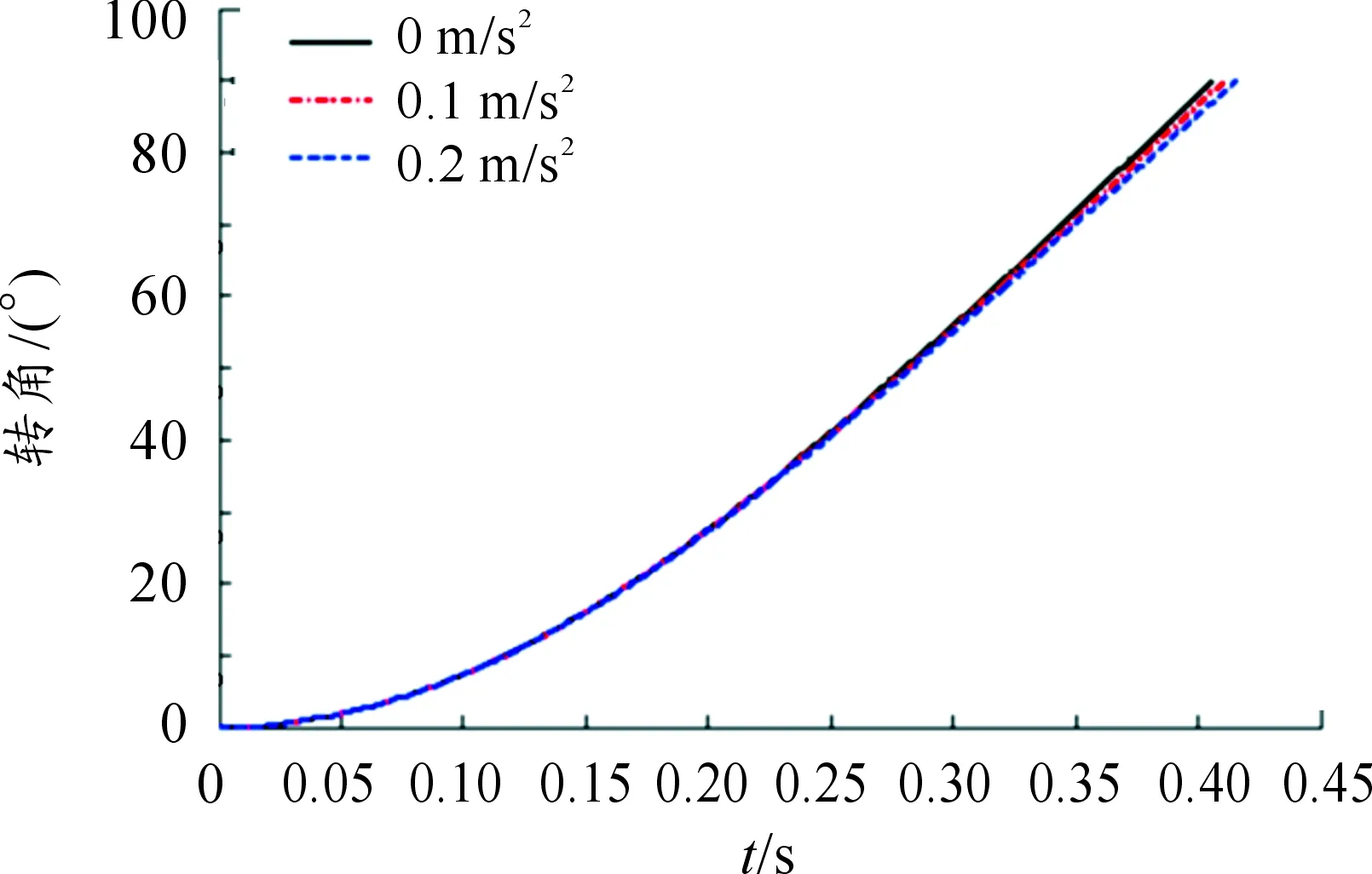
圖9 不同滑移加速度時轉角與時間的關系曲線

由圖9可知在彈體無滑移、滑移加速度為0.1 m/s2和0.2 m/s2時擺彈截止時間t分別為0.406 2 s、0.410 7 s和0.415 8 s，彈體滑移會造成力臂變長，導致擺彈運動時間延長，在機構設計時應當合理設計抱箍給彈體的預緊力，避免產生滑移。

3.4 彈體質量偏差對擺彈運動的影響

彈體存在裝藥、加工等誤差造成的質量偏差，為研究質量偏差對機構運動特性的影響，分別對質量偏差±0.2 kg的彈體進行仿真研究，結果如圖10所示。

由圖10可知在彈體質量偏差-0.2 kg、無質量偏差和質量偏差0.2 kg時擺彈截止時間t分別為0.379 5 s、0.406 2 s和0.434 4 s，彈體質量偏差對擺彈運動影響較大，隨質量偏差越大轉角與時間關系曲線偏離理想曲線越遠，造成誤差的原因是彈體質量偏差導致負載轉矩變化。

圖10 不同質量偏差時轉角與時間的關系曲線

4 結論

1) 間隙導致擺彈存在運動誤差，但間隙大小與誤差的大小并不成正相關。

2) 剛柔耦合仿真時擺臂柔性對機構運動產生誤差，在機構設計中應考慮彈性變形帶來的影響，合理選擇材料。

3) 彈體滑移導致機構運動截止時間延長，為避免滑移產生，合理設計抱箍預緊力是降低誤差的有效辦法。

4) 彈體質量偏差會影響到供彈的及時性，保證彈藥質量滿足規定能有效避免這一誤差。

5) 針對不同結構的擺彈機，轉動副間隙大小、擺臂柔性、預緊力大小的選擇與配合仍有待進一步驗證。