基于模糊理論與BP神經網絡的導彈質量評估研究

周 璐，顧均元，馮玉光

(1.海軍航空大學 研究生一隊， 山東 煙臺 264001； 2.海軍航空大學 310教研室， 山東 煙臺 264001)

導彈的質量評估工作是導彈質量監控工作的核心內容，建立好的質量評估體系能夠快速評定導彈裝備的性能狀態，了解導彈完成作戰目標的能力。在導彈的貯存期間，也可以通過質量評估結果進行有針對性的預防性維修，降低導彈的故障率與維修費用[1]。

導彈的質量狀態是一個抽象復雜的問題，質量狀態的“好”與“壞”是一個相對模糊的概念，而模糊理論中的模糊集合以及連續隸屬函數理論可以對導彈的質量狀態進行模糊評定[2]，使評定結果更加全面。BP神經網絡可以擬合復雜的非線性函數[3]，它在網絡理論以及性能方面都已比較成熟，可以用于將輸入向量按照所定義的合適方式進行分類，在導彈的綜合質量分級中可以得到相應的應用。

1 導彈質量評估模型基本框架

本文基于導彈測試數據，選用模糊理論與BP神經網絡算法建立導彈質量評估模型。具體的導彈質量評估框架如圖1所示，圖1中，ωi(i=1,2,…,n)代表各項測試數據的權重值，Fi(i=1,2,3,4)代表導彈各分系統的評分值。

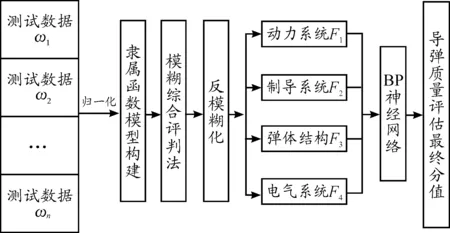
圖1 導彈質量評估總體框架

2 模糊理論在導彈質量評估中的應用

2.1 導彈質量評估指標

在實際導彈保障工作中，判斷導彈故障與否，主要是依據測試數據是否在閾值范圍內，通過測試數據來判定導彈的對應功能是否正常。導彈測試項目涵蓋了導彈各個系統的各項參數[4]，能夠較為全面地反映導彈質量特性，通過異常數據判定導彈的故障部件，或者通過測試數據在閾值范圍的分布規律判定導彈的質量狀態。

首先進行導彈測試數據的歸一化處理，將導彈的測試結果全部轉化為[0,1]之間的無量綱化值[5]。歸一化處理后的值越接近1，導彈的測試值就越接近標稱值，導彈狀態就越健康；反之，處理后的值越接近0，導彈的測試值就越接近上下限，導彈狀態就越差。

2.2 連續隸屬函數在導彈質量狀態劃分中的應用

記導彈的測試數據歸一化處理之后得到的值為x，通過蒙特卡洛統計分析[6]，得到導彈質量狀態隸屬度與測試數據之間的關系與嶺型隸屬函數最為符合。各個質量狀態對應的嶺型擬合隸屬函數分別為：

“優秀”等級對應的隸屬函數為：

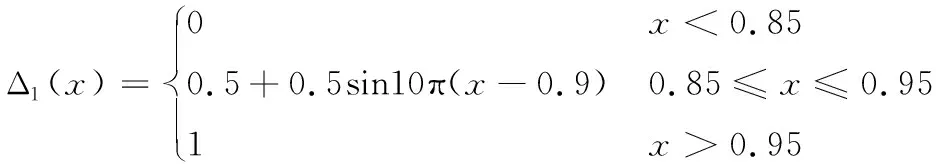
(1)

“良好”等級對應的隸屬函數為：

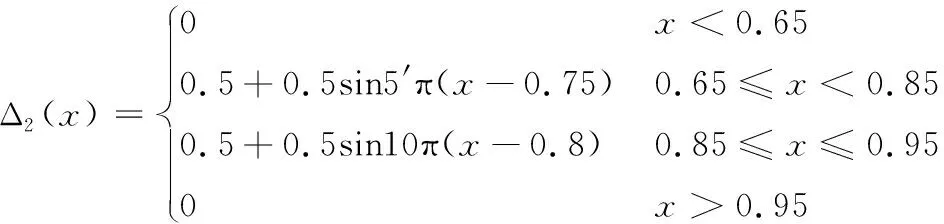
(2)

“中等”等級對應的隸屬函數為：

(3)

“較差”等級對應的隸屬函數為：

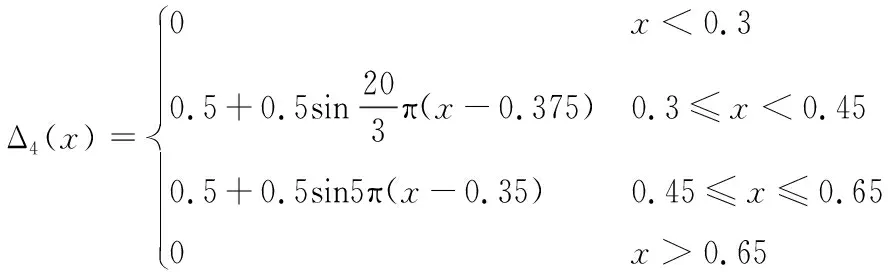
(4)

“惡化”等級對應的隸屬函數為：

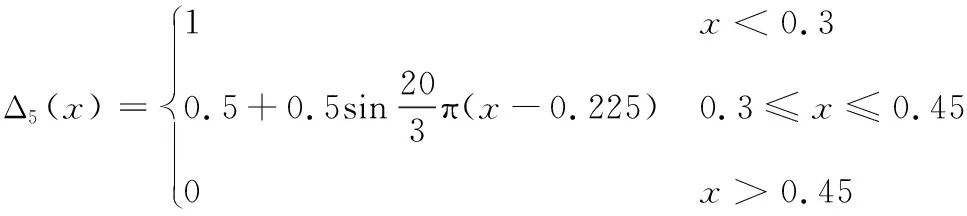
(5)

綜合上述隸屬函數公式，繪制出導彈各質量狀態的嶺型隸屬函數曲線如圖2所示。根據圖2，可以清晰地看出導彈歸一化測試數據與導彈五種質量狀態之間的隸屬函數關系，歸一化測試數據可以快速對應出相應的質量狀態等級以及對應的隸屬度大小。

圖2 導彈各質量狀態的嶺型隸屬函數曲線

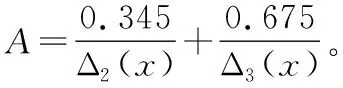
R=(0 0.345 0.675 0 0)

2.3 導彈系統質量的模糊綜合評判

本文用于導彈質量評定的四個分系統分別是動力系統U1、制導系統U2、彈體結構U3、電氣系統U4[8]。通過對每個分系統的測試，可以獲得多個項目的相應測試數據。將導彈的測試數據按照2.2節中對應的隸屬函數模型進行評價，稱為單一評價。通過各分系統對應測試項目的測試數據，對導彈系統進行整體評價，稱為綜合評價[9]。導彈系統質量就是通過對各測試數據進行綜合評價得到的。

設導彈某分系統各測試項目的權重值為w1、w2、…、wn，則這些測試項目組成的權重向量為：

w=(w1,w2,…,wn)

記第i個測試項目經過模糊化處理后得到的模糊集合為Ri=(ri1,ri2,ri3,ri4,ri5)，則n個測試項目組成的單一評判矩陣為：

則可以求得導彈某分系統的質量模糊集合X為：

X=w°R

然后對X進行歸一化，就能得到導彈某分系統對各個質量等級的隸屬度，對應模糊集合為：

2.4 導彈質量狀態模糊集合的反模糊化

對導彈系統的各個質量等級賦予一定的分值，將求出的隸屬度向量與各等級相應分數相乘并進行求和運算，獲得導彈某分系統的最終評定分值，這個過程也叫做反模糊化[10]。

設導彈某分系統的質量模糊集合X為：

(6)

式(6)中，x1、x2、x3、x4、x5分別對應質量等級的“優秀”、“良好”、“中等”、“較差”、“惡化”五個質量等級的隸屬度。按照2.2節中圖2所示的隸屬函數曲線圖，取“優秀”、“良好”、“中等”、“較差”、“惡化”五個質量等級對應相乘的分數分別為95、85、65、45、30，將每個等級的隸屬度與對應分數相乘，再求和，即可得到導彈某分系統最終的評分值。設導彈某分系統最終的評分值為F，則有：

F=95x1+85x2+65x3+45x4+30x5

五個質量等級對應的分數范圍如表1示，根據F的取值，對應出導彈對應系統的質量等級。

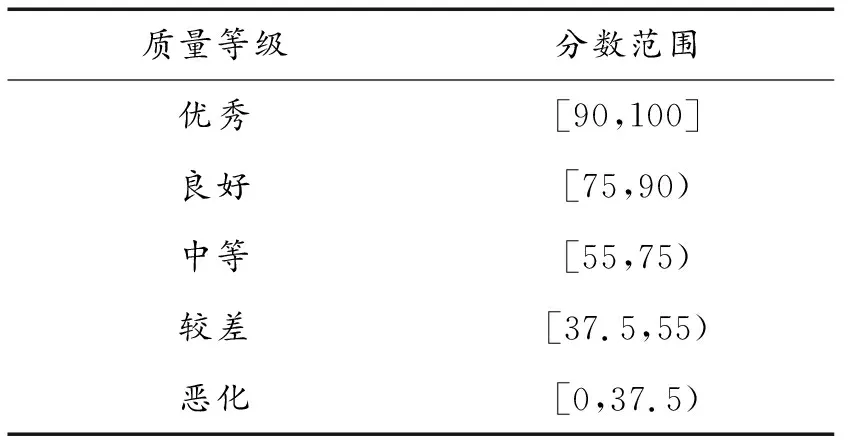
表1 各個質量等級對應的分數范圍

3 基于BP神經網絡的導彈質量評定

3.1 BP神經網絡的結構及算法

BP神經網絡是一種典型的前向網絡[11]，目前得到了廣泛的應用。BP神經網絡能夠在不事先確定輸入輸出映射關系的數學關系的前提下，學習和存儲大量的輸入輸出模式映射關系。它的學習規則是使用最速下降法，通過誤差反向傳播來不斷調整網絡的權重值與閾值，是網絡的輸出值與預期輸出值的誤差平方和最小。BP神經網絡是多層的前向網絡，最典型的是三層BP神經網絡。典型的三層BP神經網絡結構圖如圖3。BP神經網絡算法的程序流程如圖4。

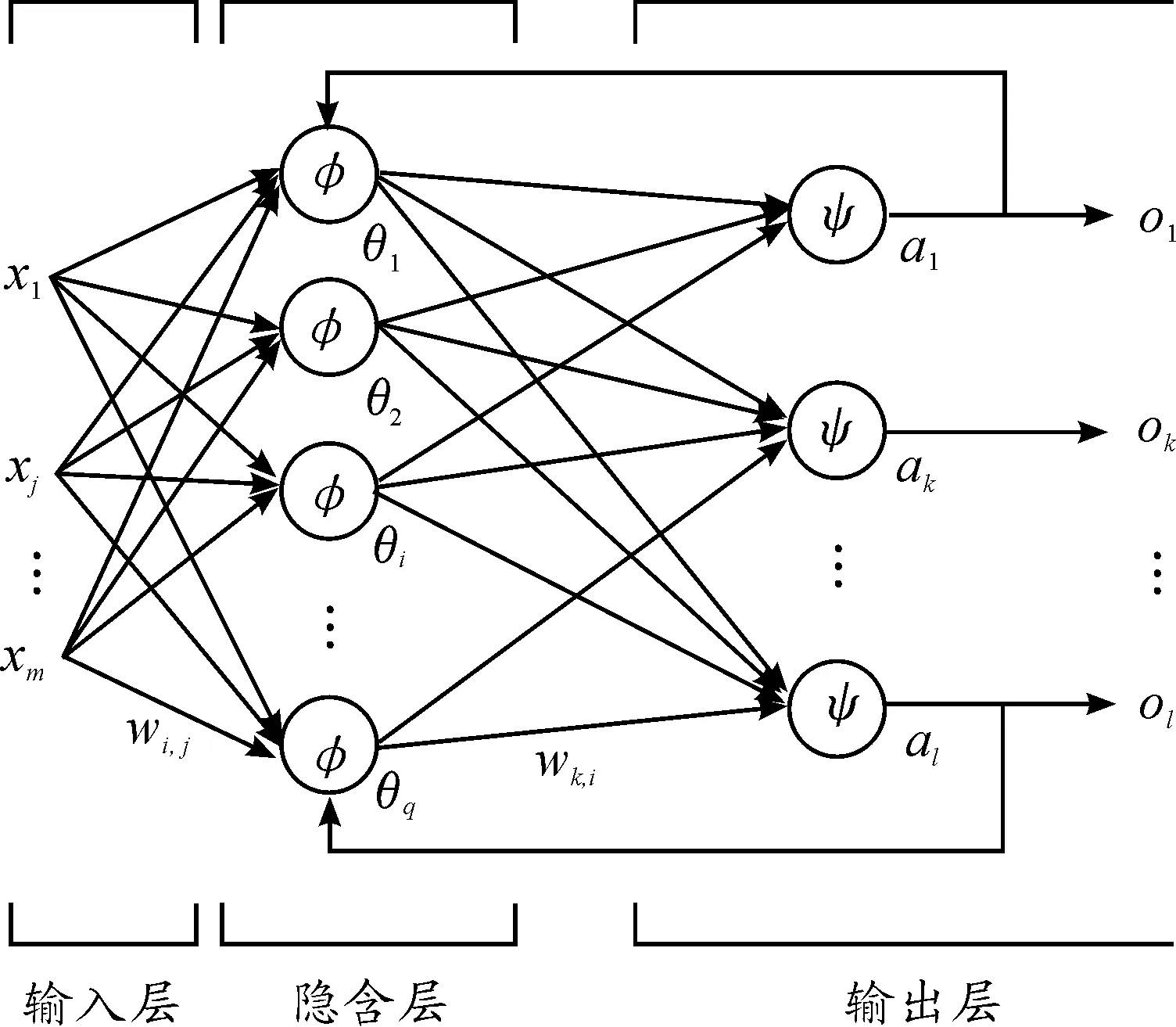
圖3 典型的三層BP神經網絡結構

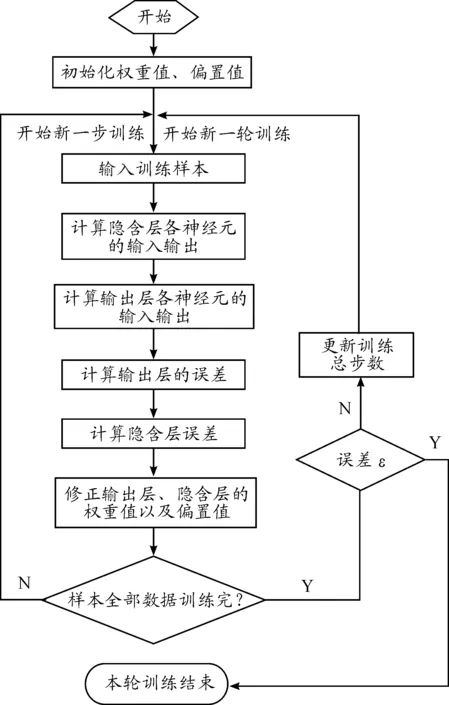
圖4 BP神經網絡算法的程序流程

3.2 數據的收集與評定模型的建立

由模糊綜合評定與反模糊化的模型構建可知，導彈某分系統最終的評分值可以計算得出，并對應出相應的質量等級。導彈能質量評定的四個分系統分別是動力系統U1、制導系統U2、彈體結構U3、電氣系統U4，其對應的模糊評定的最終評分值分別為F1、F2、F3、F4。根據導彈四個分系統的評分值對實現導彈系統最終質量等級的評定是質量評定的最終目的。選用BP神經網絡作為評定模型。整個神經網絡的輸入為四個分系統經過模糊評定之后的評分值，輸出為導彈整體的質量評分值。首先使用專家系統對評定結果進行綜合評定，根據對應數值訓練出學習網絡，再采用客觀模型對經過模糊處理的實際評分值進行預測評定，主觀性客觀相結合評定結果具有更高的可信度。

選取10位在導彈質量評定方面威望極高的專家[12]，根據50組導彈四個分系統的評分值對導彈最終的質量等級進行評定。除去10位專家評分的最大值以及最小值，對剩余的數據求平均值并取整，就是導彈質量評定的最終結果。具體數據以及專家最終評定結果如表2所示。

表2 導彈各個系統的評分值以及對應的專家總體評分值

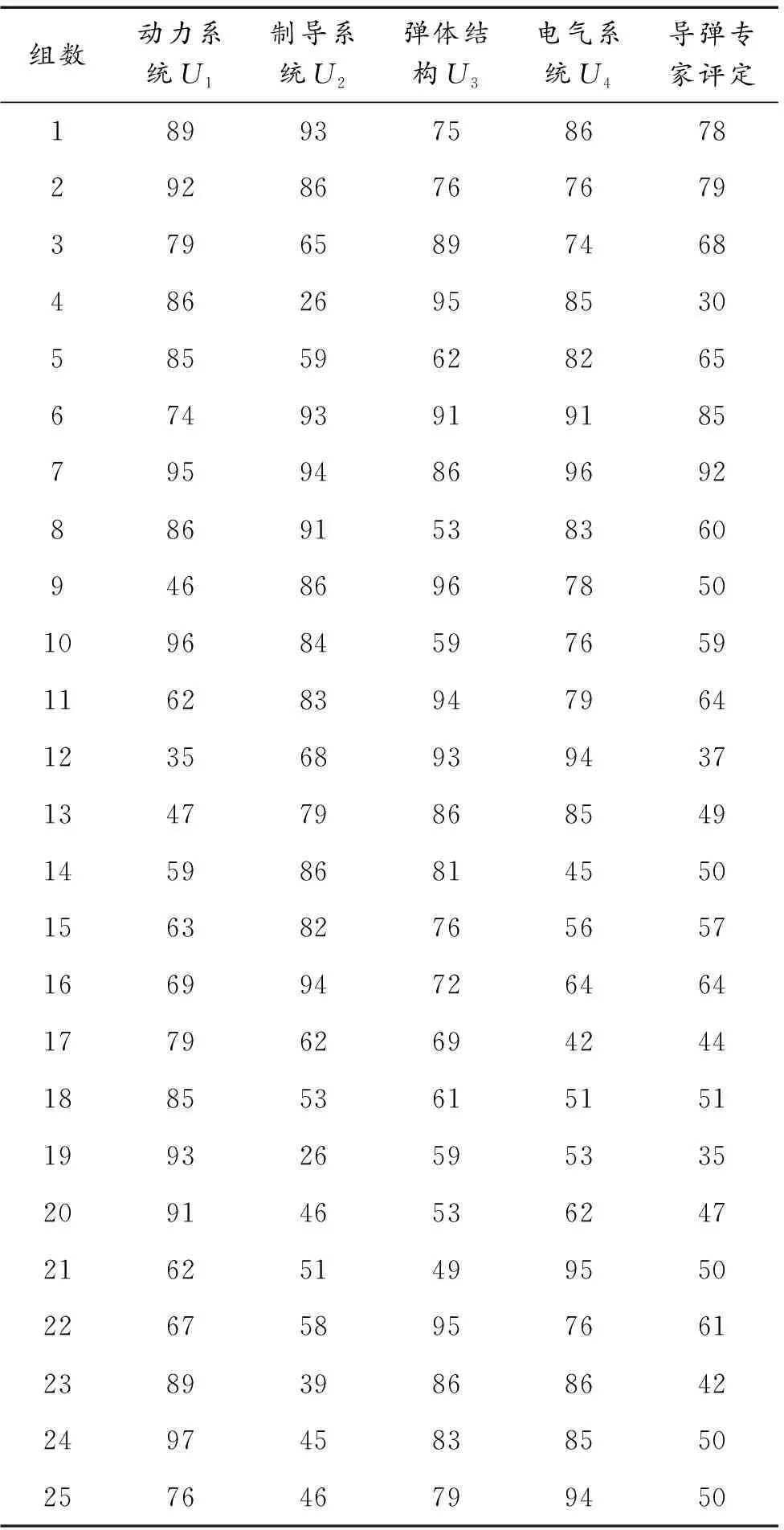
組數動力系統U1制導系統U2彈體結構U3電氣系統U4導彈專家評定189937586782928676767937965897468486269585305855962826567493919185795948696928869153836094686967850109684597659116283947964123568939437134779868549145986814550156382765657166994726464177962694244188553615151199326595335209146536247216251499550226758957661238939868642249745838550257646799450

組數動力系統U1制導系統U2彈體結構U3電氣系統U4導彈專家評定263678598637275972359236286981647964297284618162307689214625319895465948328292169425337893798579345646948350355447928650363949868140374978897650388986975259399259918165408791936469419392863845426593849469438986818182443487757636452589737931466569649164474986699355484789599048496995986065509296917680

在BP神經網絡的選擇上，選擇三層BP神經網絡結構模型。根據表2的數據內容，使用前40組數據進行網絡訓練，使用后10組數據進行網絡測試。在網絡訓練以及測試的過程中，整個網絡的輸入為動力系統U1、制導系統U2、彈體結構U3、電氣系統U4的評分值，即輸入4個數；整個網絡的輸出為1個數，代表導彈的最終質量評分值。整個評價系統的神經網絡結構模型如圖5所示。

圖5 神經網絡結構圖

3.3 BP神經網絡參數的設置

3.3.1隱含層個數選取問題

隱含層個數選取問題是對BP神經網絡的一個優化過程。一般而言，隱含層個數越多，即能夠降低整個網絡的訓練誤差，又可以提高精度，缺點就是會增加網絡的復雜性，增加訓練時間，過多的隱含層個數還會使網絡出現過擬合的現象[13]。因此在滿足訓練精度的前提下，盡可能選取合理的隱含層個數，使網絡的結構盡可能緊湊。

一般計算隱含層節點數的經驗公式有：

(7)

m=log2n

(8)

(9)

m=2n+1

(10)

式(7)～(10)中，m為隱含層節點數；n為輸入層節點數；l為輸出層節點數；α為1～10之間的常數。

表3 隱含層個數以及對應的預測均方誤差

由表3數據可得，當隱含層個數m=11時，網絡測試的均方誤差值最小，因此選擇隱含層的個數m=11。

3.3.2BP神經網絡模型建立及部分參數設置

隱含層的傳遞函數選用tansig函數，也就是雙極正切S形函數。

輸出層的傳遞函數選用purelin函數，也就是線性函數。

f2(x)=x

部分參數設定如下：

神經網絡的學習率為0.1；動量因子為0.9；最大迭代次數設置為10 000；最終的訓練目標為輸出值與實際值的均方誤差不大于0.000 1%。

3.3.3 BP神經網絡訓練的最佳迭代次數

通過多次訓練，得到最佳迭代次數為13，其中參數設置如圖6所示。

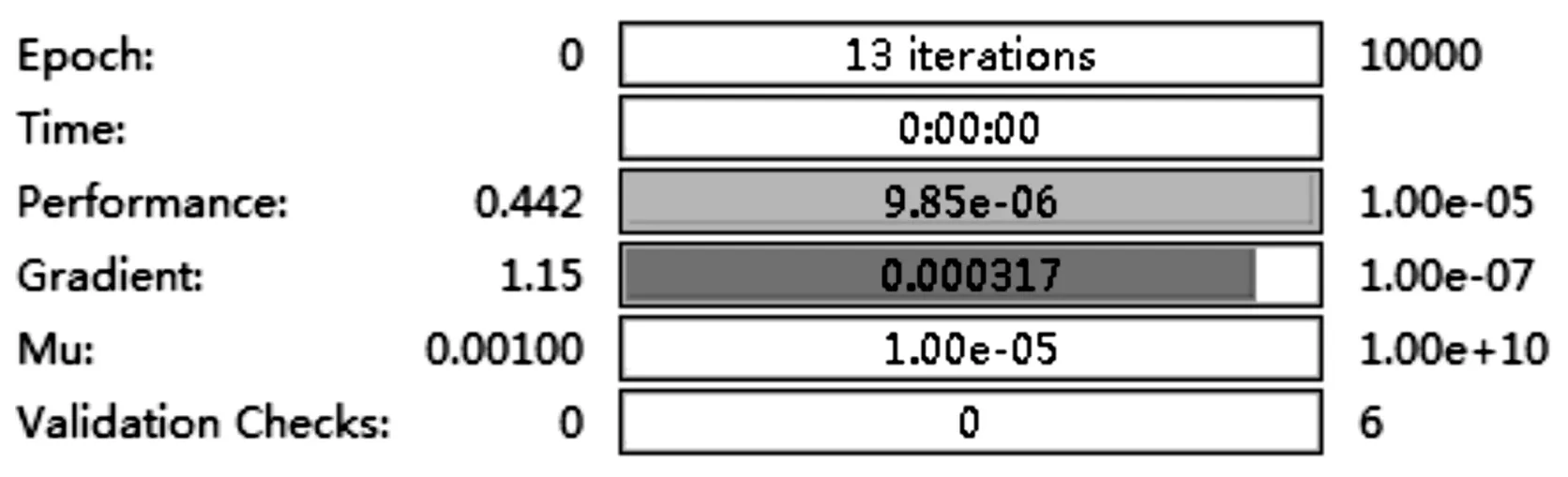
圖6 迭代次數為13時對應的參數設置

迭代次數與對應的均方誤差曲線如圖7所示。

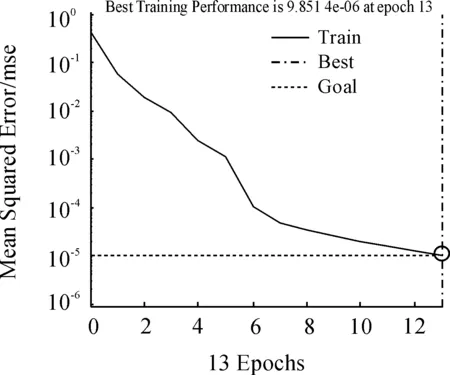
圖7 迭代次數與對應的訓練均方誤差曲線

由圖7可知，當迭代次數為13時，訓練誤差達到訓練目標要求，即完成訓練。將迭代次數13進行固定，用于后期的網絡預測過程。

3.4 BP神經網絡的仿真程序實現

按照以上設定的各個參數對神經網絡進行訓練，將表2中的前40組數據代入，得到訓練輸出結果與預期值的擬合曲線，如圖8所示。由圖8可知，訓練輸出的結果與預期值的擬合效果良好。

圖8 訓練過程神經網絡預測值與真實值擬合曲線

將表1中的后10組數據代入訓練好的神經網絡中進行測試，得到神經網絡測試過程的預測值與真實值擬合曲線，如圖9所示。

圖9 測試過程神經網絡預測值與真實值擬合曲線

測試樣本的相對誤差曲線如圖10所示。由圖10可知，樣本1的相對誤差較大，樣本2到樣本10的相對誤差較小。說明神經網絡能夠較為準確地預測絕大多數數據，使用訓練完畢的BP神經網絡可以得出合理的導彈質量評分值。部分樣本的預測結果偏差較大的原因是網絡訓練樣本數據庫不夠全面，增加訓練樣本數可以提高整個網絡預測的準確度。因此可以將BP神經網絡的學習樣本增加，使其完全包含實際導彈質量評定過程中可能出現的導彈系統評分值，減小使用網絡預測時的相對誤差值。

在實際評估過程中，將已知的導彈四個分系統的評分值輸入已經訓練完畢的BP神經網絡中，就可以得到導彈質量評分值。對應2.4節中表1的內容，可以確定導彈的具體質量狀態。給出導彈系統質量評定的結論。

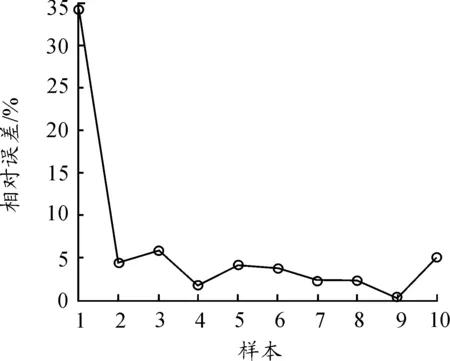
圖10 測試樣本的相對誤差曲線

4 結論

在導彈的質量評估工作中，運用模糊隸屬函數、模糊集合以及BP神經網絡理論結合的評估模型，能夠完美地綜合導彈測試數據和函數模型的客觀性、模糊集合的全面性、專家評分的主觀性以及神經網絡的準確性，避免單一評價模型的片面性，有利于合理地分析、判斷導彈當前的質量狀態，應用于導彈質量狀態評估工作。