轉管炮機心結構參數化分析

原 平，戴勁松，王茂森

(南京理工大學 機械工程學院， 南京 210000)

轉管炮機心組在星形體導軌和炮箱凸輪曲線槽的共同作用下做循環往復運動，完成射擊循環動作。不同炮管數量的轉管炮射速可達1 500～10 000發/min，機心組自動循環時間短，運動狀態變化劇烈。在某型轉管炮射擊實驗中，發現機心組運動卡滯，機心滾輪與炮箱凸輪曲線槽之間以及機心與星形體導軌之間的磨損較嚴重。關于減少機心滾輪與炮箱凸輪曲線槽之間的正壓力、降低驅動功耗方面，前人研究的重點在于對炮箱凸輪曲線槽的優化設計上。文獻[1-2]通過對炮箱凸輪曲線槽過渡段進行優化設計，使得機心滾輪與凸輪曲線槽間的接觸力降低。文獻[3]研究了機心主滾輪在機體上的布局對機心滾輪和炮箱凸輪曲線槽之間接觸力的影響。文獻[4]主要對星形體導軌傾角進行了研究，而對機心結構沒有進行較為細致的研究。為了解決上述實驗中出現的問題，展開對轉管炮機心結構的研究，根據達朗貝爾原理[5]，列出機心受力的動平衡方程，應用Matlab編程分析機心結構參數的變化與機心滾輪和炮箱凸輪曲線槽正壓力之間的關系。

1 動力學分析

1.1 機心運動過程分析

機心組在轉管炮凸輪曲線槽約束下做循環往復運動，運動特性取決于轉管炮凸輪曲線槽的特征。根據轉管炮循環圖，轉管炮凸輪曲線槽分段設計[6]，凸輪槽展開如圖1所示。在一個射擊循環中，θ1為輸彈加速段，θ2為輸彈等速段，θ3為輸彈減速段，θ4為擊發過程直線段，θ5為退殼加速段，θ6為退殼等速段，θ7為退殼減速段，θ8為進出彈直線段。所以在一個射擊循環，機心組經歷兩次直線段，兩次加速段，兩次減速段、兩次等速段[7]。取機心組其中一個機心為研究對象，不考慮彈丸的情況下，分析各個過程機心的動力學。

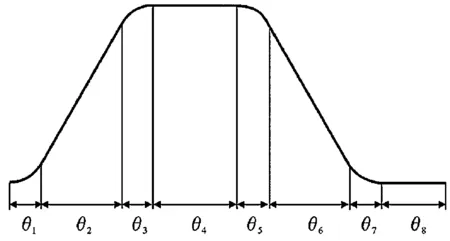
圖1 凸輪槽展開示意圖

1.2 機心動力學分析

1) 機心加速段動力學分析

機心滾輪與凸輪曲線槽加速段受力分析可得，凸輪曲線槽對滾輪的正壓力為N，方向垂直于凸輪曲線槽接觸面，機心滾輪按純滾動處理，所受到的摩擦力為f1N，方向沿凸輪曲線槽切線方向，與運動方向相反。f1為滾動摩擦系數。將正壓力和摩擦力投影，分解為沿著機心軸向運動方向的主動推力Nx和垂直于運動方向橫向力Ny，其中α為壓力角：

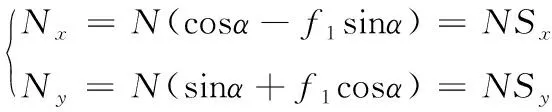
(1)

其中令：

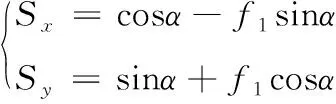
(2)

機心的主要設計結構參數以及加速段受力分析如圖2所示，O點為機心中心，在身管軸線延長線上，B點為機心滾輪理想受力點，A點為導軌對機心側向正壓力N1作用延長線與O、B連線的交點，D、D′點為導軌對機心作用中心點。令A點和B點連線長度為h0，O點和B點連線長度為h，O點與D，D′連線的垂直距離為h1，h1在O點以下為負值，在O點以上取正值。A點和D點連線長度為L0，C為D，D′連線長度，L為機心縱向長度，θ為星形體導軌傾角。當轉管炮凸輪曲線槽和身管組中心圓給定之后，h等于機心滾輪公轉半徑減去身管組中心圓半徑。機心縱向長度L取決于凸輪的軸向長度，研究機心結構參數影響就集中在星形體導軌傾角θ、機心徑向寬度C、導軌理想作用點高度h1上。

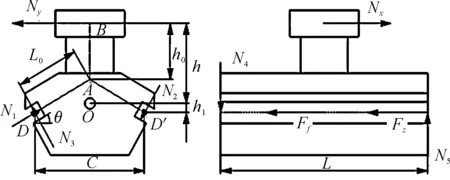
圖2 機心受力分析示意圖

由幾何關系可得：

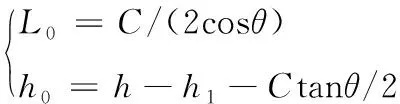
(3)

機心加速段受力分析可得，在機心主視圖上，機心受到星形體導軌正壓力N1、N2、N3，作用點和方向如圖上所示。根據受力列出機心主視圖的力平衡方程：

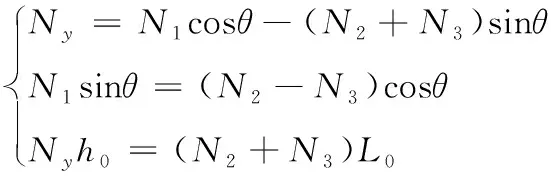
(4)

在機心左視圖上，機心受到星形體導軌正壓力N4、N5，作用點和方向如圖上所示。圖中Ff為星形體導軌對機心正壓力以及由機心離心力和切向慣性力引起的摩擦力，f2為星形體導軌與機心之間的摩擦系數，m為機心質量，r為身管組中心圓半徑，ω為星形體轉動角速度，ε為星形體轉動角加速度。

(5)

在機心加速度反方向施加達朗伯力Fz得到機心左視圖動平衡方程：

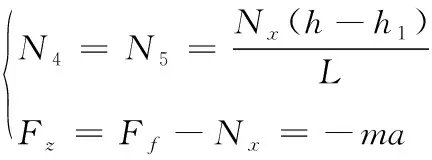
(6)

由式(1)～(6)聯立可得在機心加速段運動中凸輪曲線槽對滾輪的正壓力N：

(7)

其中：

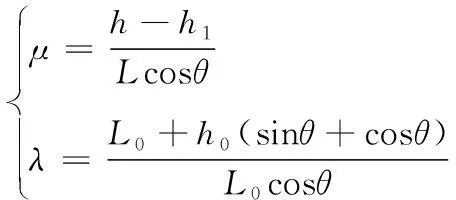
(8)

2) 機心減速段動力學分析

機心在減速段運動時，凸輪曲線槽對滾輪的正壓力N與機心軸向運動方向相反，受力分析計算可得，只需將f1變為-f1，f2變為-f2即可得到在機心減速段運動中凸輪曲線槽對滾輪的正壓力N：

(9)

其中μ，λ同上。

3) 機心等速段動力學分析

機心運動到等速段時，機心加速度為0，這時機心等速段運動中凸輪曲線槽對滾輪的正壓力N為：

(10)

其中μ，λ同上。

4) 機心直線段動力學分析

機心運動到直線段時，機心軸向位移為0，這時機心直線段運動中凸輪曲線槽對滾輪的正壓力N為0。

2 實例分析

2.1 參數化計算

以某型轉管炮為例，其炮箱凸輪曲線槽是按照擺線修正梯形加速度運動規律設計，擺線修正梯形加速度運動規律的類加速度曲線沒有突變現象，因此從動件沒有剛性和柔性沖擊[8-10]。位移和壓力角曲線如圖3。

身管組中心圓半徑r=50 mm，機心滾輪公轉半徑r1=78 mm。機心的結構參數：機心中心O到機心滾輪理想受力點A的距離h=28 mm，機心縱向長度L=80 mm，星形體導軌傾角θ∈[0°,45°]、機心徑向寬度C∈[35,50]，導軌理想作用點高度h1∈[-8,8]，機心質量m根據具體的結構尺寸計算得到。凸輪曲線槽與機心滾輪之間的滾動摩擦系數f1的取值根據機械手冊[11]：f=μg/R，μg為滾動摩擦力臂，鋼與鋼的滾動摩擦力臂一般取值為0.2～0.4，R為滾動摩擦半徑，實例中的機心滾輪半徑R=12.5 mm，得到f1=0.03。機心與星形體導軌之間的滑動摩擦系數取f2=0.1。這里只研究轉管自動機穩定工作的情況，星形體角加速度ε=0。加速度a和壓力角α根據凸輪曲線方程計算得到。

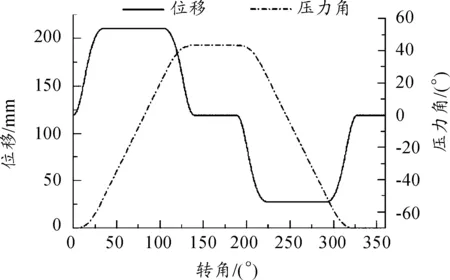
圖3 凸輪曲線槽位移和壓力角曲線

當射速為4 000發/min時，計算得到對應的角速度ω=104.72 rad/s。應用Matlab中的surf函數，帶入數據得到C、h1、θ結構參數的變化對機心滾輪與凸輪曲線槽之間的正壓力最大值的變化情況，X坐標為C，Y坐標為h1，Z坐標為Nmax，如圖4所示。當分別取C、h1等于其取值范圍最大最小值，研究隨著θ的變化，正壓力最大值的變化情況，如圖5所示。當C，h1分別取最小與大值時，Nmax隨ω變化情況，如圖6所示。

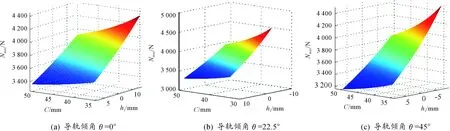
圖4 不同傾角θ，Nmax隨C、h1變化情況

2.2 計算結果分析

從圖4可以看出，當星形體導軌傾角一定時，隨著機心徑向寬度C以及導軌理想作用點高度h1的增大，機心滾輪與凸輪曲線槽之間的正壓力最大值成規律性變化，其最大值逐漸減小。正壓力Nmax的最大值位于C=35 mm，h1=-8 mm處，即C、h1取得其取值范圍的最小值時。正壓力Nmax的最小值位于C=50 mm，h1=8 mm處，即C、h1取得其取值范圍的最大值。

由圖5可以看出，當機心徑向寬度C以及導軌理想作用點高度h1分別取最小與最大值時，Nmax隨θ變化情況。θ從0°到45°變化中，C、h1取最大值時，可以看出Nmax先增大后減小，Nmax最小等于4 315.2 N，此時導軌傾角θ=0°。當C、h1取最大值時，Nmax隨著θ的增大而逐漸減小，Nmax最小等于3 154.7 N，此時導軌傾角θ=45°。正壓力減小幅度26.9%。可以得出要使機心滾輪與凸輪曲線槽之間的正壓力減小，應選取較大的機心徑向寬度C以及導軌理想作用點高度h1。

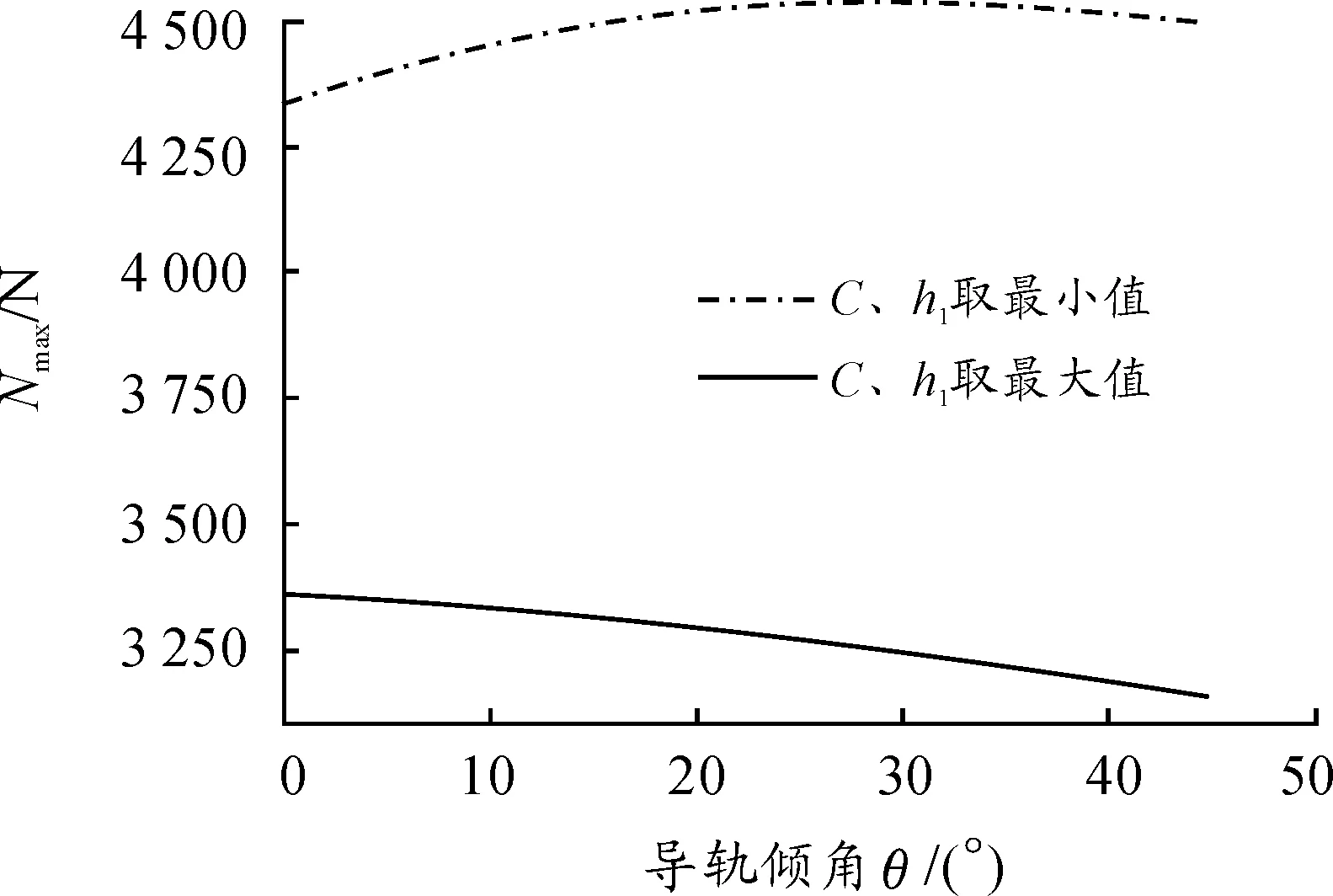
圖5 C、h1取最小值與最大值時，Nmax隨θ變化情況

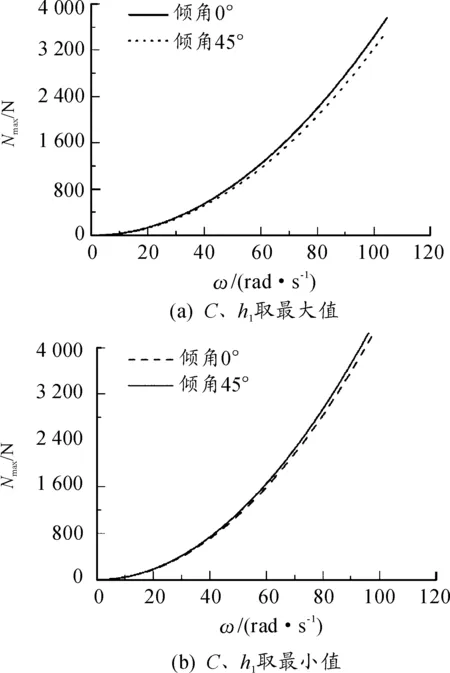
圖6 當C、h1取最小與大值時，Nmax隨ω變化情況

由圖6可以看出，當機心徑向寬度C以及導軌理想作用點高度h1分別取最小與最大值時，Nmax隨ω變化情況。隨著轉管炮射速的提高，角速度增大，Nmax增長速度由慢變快，傾角變化對Nmax的影響也越來越大。當C、h1取最大值時，星形體導軌傾角45°的Nmax小于導軌傾角0°的Nmax，當C、h1取最小值時，星形體導軌傾角45°的Nmax大于導軌傾角0°的Nmax。得出當機心選取較大的徑向尺寸和導軌理想作用點高度時，導軌傾角越大越好，反之，水平最好。

由以上分析，取C=50 mm，h1=8 mm，θ=45°，機心滾輪與凸輪曲線槽之間的正壓力最小，星形體旋轉一周，機心滾輪與凸輪槽正壓力變化曲線如圖7之實線，圖7之虛線為原設計C=40 mm，h1=-5 mm，θ=30°的機心滾輪與凸輪槽正壓力變化曲線。原機心模型Nmax=4 065.9 N，新機心模型Nmax=3 154.7 N，最大減小幅度為22.4%。

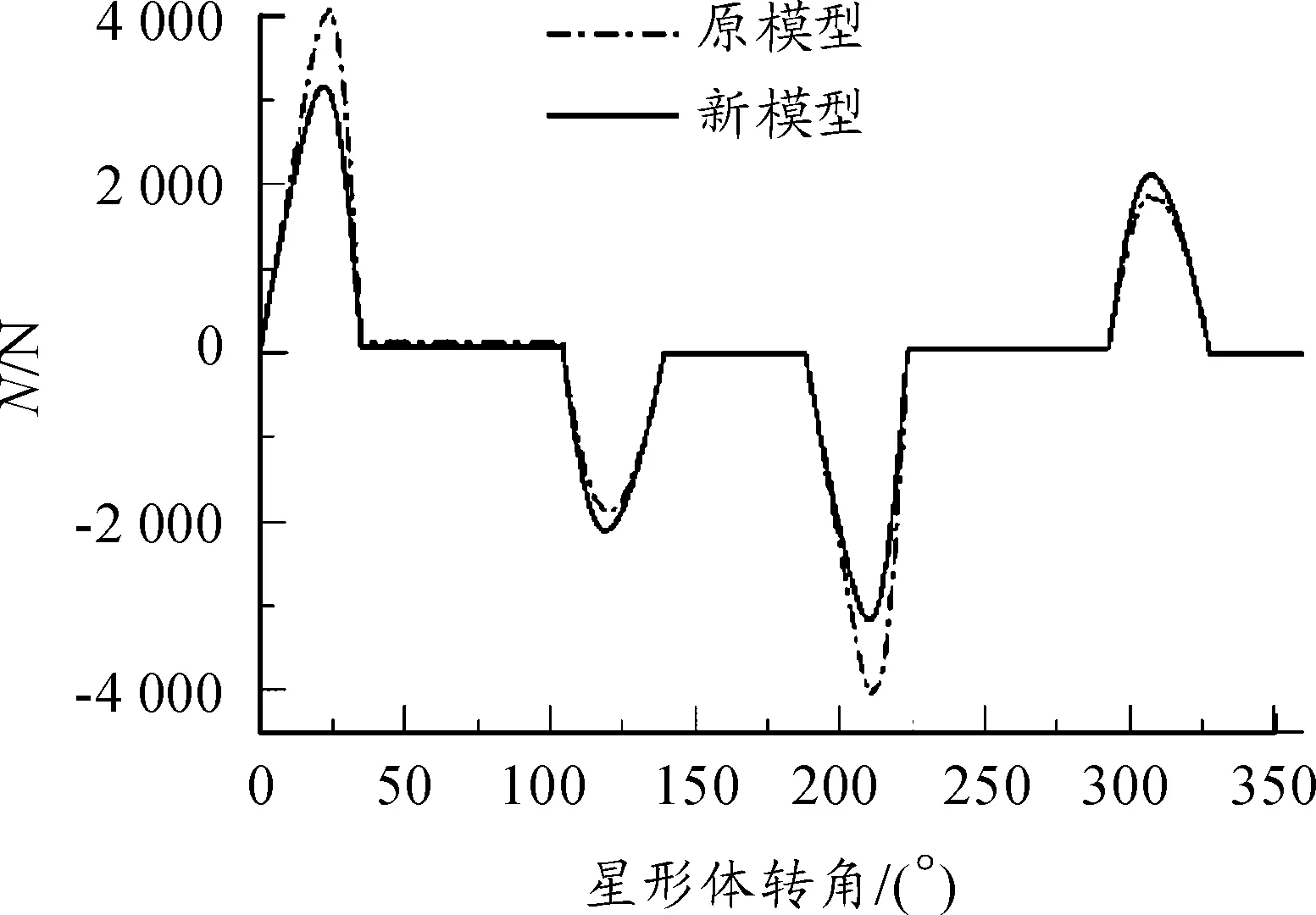
圖7 原模型與新模型正壓力曲線

3 結論

在對某轉管炮進行動力學分析的基礎上，通過參數化分析，得到了機心結構參數的改變對機心滾輪與轉管炮凸輪曲線槽的正壓力的變化規律。為了得到較小的正壓力，減小驅動功耗，機心與導軌接觸的徑向寬度應盡量選較大的尺寸，導軌對機心作用中心點應位于機心中心以上，距離機心中心點越遠，正壓力越小。當機心選取較大的徑向尺寸和導軌理想作用點高度時，導軌傾角越大越好，反之，水平最好。