基于改進克隆選擇算法的區域交通燈配時優化

陳海洋，金曉磊，牛龍輝，劉喜慶

西安工程大學 電子信息學院，西安710600

1 引言

交通作為城市經濟活動的命脈，對促進社會發展、提高人民生活水平具有十分重要的意義，但隨著城市居民汽車擁有量的不斷攀升，交通擁堵現象在我國很多城市都日益嚴重。在基礎設施建設周期漫長且耗資巨大的情況下，充分利用現有的路網資源、優化交通信號控制對解決城市交通擁堵問題的重要性不可低估。

交通燈是城市交通信號控制的最重要組成部分，目前國內外已有許多關于智能交通燈的研究工作，而依據實時交通流動態設置交通燈狀態正是最常用的方法之一[1-4]。Wu 等[5]提出了基于霧計算的交通燈智能控制系統，它的主要思想是通過霧計算平臺來計算和分享當前路口及周圍路口的實時車流量信息，并以實時車流量作為參數，設計交通燈智能控制算法，使相鄰路口的交通燈周期實現相互協調、共同優化。Shaghaghi等[6]提出了一種基于車載自組網的自適應交通控制系統，該控制系統以交叉口處的車輛排隊長度為交通評估依據，并采用車對車通信技術與車對基礎設備通信技術進行車輛密度計算、信息傳遞。Muntaser 等[7]提出一種基于模糊系統與車輛通信技術的交通信號控制策略，將信號控制問題轉化為邏輯問題而不是優化問題，并證明提出的控制策略性能是優越的。Sun 等[8]提出了一種基于車聯網（IOV）的動態交通控制與誘導協同優化模型，該模型包含三層，其中上層模型通過遺傳算法求解，中層模型和下層模型通過連續平均法求解。Zhao 等[9]提出一種基于遺傳算法和機器學習的交通燈實時調度算法，該算法根據交叉口的實時交通流來調度每個交通燈的時間相位，同時考慮每個交叉口下一個時間段的車流量，此車流量數據采用線性回歸算法預測，仿真結果表明該調度算法通過減少路網中所有行駛車輛的總等待延誤提高了路網的交通流暢性。

區域交通燈配時控制優化屬于全局優化問題，遺傳算法等智能優化算法對解決多變量全局尋優問題具有明顯優勢，因此，近年來許多學者將遺傳算法及其改進算法應用于交通優化研究領域[10-13]。而與遺傳算法同為進化類智能優化算法的免疫克隆選擇算法同樣具有很強的全局搜索能力，但在交通控制方面的應用則較少。相比于遺傳算法只考慮到個體的適應度，免疫克隆選擇算法既考慮抗體與抗原間的親和度，也考慮抗體濃度；遺傳算法只有變異和交叉操作，而免疫克隆選擇算法具有獨特的克隆操作算子、種群更新算子。因此本文考慮將免疫克隆選擇算法應用于區域交通燈配時優化，并以西安市某區域路網為研究參考對象，提出一種基于改進免疫克隆選擇算法的交通燈實時配時方法。本文提出的配時方法以區域路網中所有路口總滯留車輛數最小為優化目標，將交通燈狀態設置問題轉換成免疫克隆選擇算法搜索最優解問題，并將克隆選擇算法編碼和解碼過程融入到交通燈配時控制場景中，提升了路網的交通效率，對減輕城市道路通行壓力、保障市民出行暢通具有重要的意義。

2 改進的免疫克隆選擇算法

免疫算法是受生物免疫學啟發，模擬免疫系統工作原理來解決現實生活中復雜問題的智能算法[14]。克隆選擇算法是其中的一個重要研究方向，主要思想是將現實問題和問題的解分別抽象為克隆選擇學說中的抗原和抗體，通過選擇、克隆、變異等一系列操作來進行最優解的搜索。

免疫克隆選擇算法以激勵度來衡量抗體質量的優劣。激勵度的計算需綜合考慮抗體親和度與抗體濃度，計算公式通常如式（1）所示：

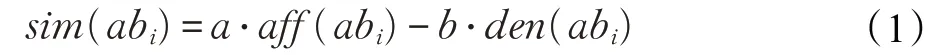
式中，sim(abi)為抗體abi的激勵度；aff(abi)為抗體abi的親和度；den(abi)為抗體abi的濃度；a、b為計算參數，根據實際情況確定。從式（1）中可以看出，抗體的親和度值越高、濃度值越低，其激勵度值就越高。抗體濃度值高，意味著當前種群中相似個體較多，對其進行一定抑制可以更好地保證種群的多樣性，使最優解的搜索不會只局限于一小片區域。

針對免疫克隆選擇算法在尋優過程中收斂速度較慢的問題，本文提出了兩個改進點：一是利用雙層動態變異算子對種群中抗體進行變異；二是對克隆抑制算子和種群刷新算子進行了改進。

（1）雙層動態變異算子

在標準免疫克隆選擇算法中，抗體的變異概率一般取一較大的確定值，高頻率的變異是抗體種群多樣性和親和度成熟的重要保證。但在尋優迭代過程的后期，較大的變異概率會使得算法缺乏局部搜索，并且有一定可能對當前種群中已經尋得的優秀抗體造成破壞。因此，在許多學者的研究中，都采用了動態變異算子，即變異概率會隨著迭代次數增加而動態調整。

本文提出的雙層動態變異算子是指變異概率會隨著種群迭代次數的增加而線性遞減。且在同一代中，被選擇出來進行克隆的父代抗體在當代種群中激勵度排名越靠前，對它的所有克隆副本以更小的概率進行變異，反之，父代抗體在當代種群中激勵度排名越靠后，對它的所有克隆副本以更大的概率進行變異。變異概率值的第一層動態調整是基于迭代次數，使得算法既能在前中期快速、大范圍尋優，也能在后期進行更多局部搜索且有更大概率穩定收斂于全局最優解；變異概率值的第二層動態調整是基于每一代中父代抗體的激勵度排名，既能對不夠優秀抗體的克隆副本進行較大的變異以搜索更優秀的抗體，又能盡可能地保護優秀抗體的克隆副本不受太大的破壞得以傳到下一代。

（2）改進的克隆抑制算子與種群刷新算子

標準免疫克隆選擇算法的運算過程大致如下：種群個體數為NP，先進行選擇操作，即挑選出種群中激勵度排序靠前的k 個抗體，再對這k 個抗體進行克隆、變異操作。之后對變異結果進行再選擇，即克隆抑制，剔除親和度較低的抗體，僅保留親和度最高的k 個抗體。最后進行種群刷新，即隨機生成NP-k個新抗體，與經過克隆抑制保留下來的k個抗體組合，形成新一代種群。

用隨機生成的新抗體，來替代選擇操作中被淘汰的次優抗體，可以大幅提高種群的多樣性。但隨機生成的新抗體親和度好壞程度不定，不利于加速種群收斂。對此，本文提出了改進的克隆抑制算子與種群刷新算子：種群個體數為NP，先選擇種群中激勵度排序靠前的NP/2個抗體，再進行克隆、變異操作，之后進行克隆抑制，每個父代抗體的所有克隆副本僅保留親和度最高的兩個，這樣被保留下來的抗體共有NP 個，這NP 個抗體就是新一代的種群。如此的克隆抑制與種群刷新機制，可以大幅提高算法收斂速度，但需配合較大的克隆倍數值并應用動態變異算子，否則種群的多樣性得不到保障，容易陷入局部最優。

綜上所述，本文提出的改進免疫克隆選擇算法的完整運算過程可描述如下：

（1）隨機生成初始抗體種群。

（2）判斷是否滿足迭代終止條件：若滿足，則終止算法運算，輸出末代種群中的最優解；若不滿足，則執行步驟（3）。

（3）計算當前種群中所有抗體的激勵度值，并按降序排序。

（4）選擇排序靠前的一半抗體，對它們以相同的倍數進行克隆復制。

（5）利用雙層動態變異算子對克隆得到的副本進行變異操作。

（6）利用上文提出的改進的克隆抑制算子與種群刷新算子進行克隆抑制、種群刷新，再轉入步驟（2）。

3 基于改進克隆選擇算法的區域交通燈配時方法

傳統的固定配時交通燈只是機械地變換信號，不能根據當前交通路網中的車流狀況進行靈活調整，導致時常出現一個路口綠燈長亮方向無車通過，而紅燈長亮方向則排起長長車隊的現象。而目前隨著檢測傳感器[15]、車載衛星定位[16]、射頻模塊[17]和視頻圖像檢測[18]等技術的發展，實時車流信息的獲得不再是問題。因此，本文的研究工作就是將智能優化算法應用到區域交通燈配時方案中，根據實時獲取的車流量信息，靈活地對區域交通燈配時，使得區域交通狀況能得到顯著優化。

本文以西安市某區域一個包含36 個十字路口的路網為研究參考對象。為方便具體研究，對這36 個路口進行標識，標識名為C1～C36。

一片區域內所有十字路口的交通燈狀態設置是一個復雜的實際問題，難以直接應用智能優化算法，需要先從復雜的實際問題中找出最關鍵的控制因素。通過調研本文研究的區域路網，發現這片區域中C1～C21 路口為二相位控制，C22～C36 路口為四相位控制，相位圖分別如圖1、2 所示（右轉彎不考慮）。基于以上各路口的相位調研情況，則可將區域內所有路口的交通燈狀態設置問題，轉換成在不同時間確定各個路口哪一個相位獲取通行權的問題。

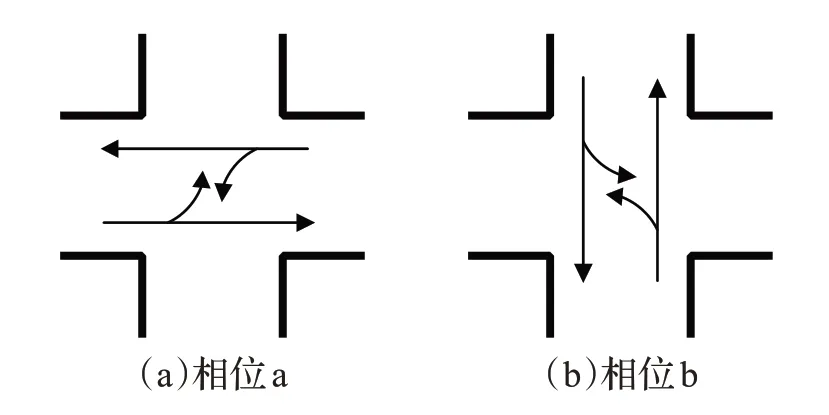
圖1 路口C1～C21相位圖

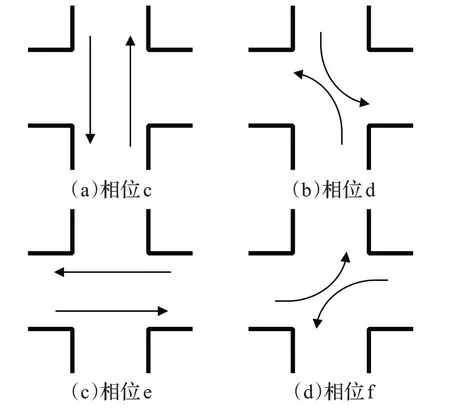
圖2 路口C22～C36相位圖

為了實現區域交通燈的配時優化，本文提出一種基于改進免疫克隆選擇算法的區域交通燈實時配時方法，采用克隆選擇算法搜索最優解，最優個體解碼后其表現型轉換成對應各個路口交通燈狀態。克隆選擇算法的過程大致為：首先，初始化初代種群；隨后，通過激勵度評估來篩選種群個體；最后，借助免疫算子，產生下一代個體，生成代表新的潛在解集的種群直至進化到最高代種群。為了實時控制交通燈，需要利用克隆選擇算法和各路口的實時交通流數據，找到使在單位時間T 內各個路口滯留車輛數總和達到最小的交通燈配時方案。配時方法具體描述如下：

（1）基因編碼和初始化種群

①基因編碼：表現型到基因型映射

對于二相位的路口，使用二進制編碼表示基因型，用“0”代表相位a，用“1”代表相位b。所以從表現型到基因型的映射就是相位a對應“0”，相位b對應“1”。

對于四相位的路口，同樣使用二進制編碼表示基因型，用“00”代表相位c，“01”代表相位d，“10”代表相位e，“11”代表相位f。所以從表現型到基因型的映射就是相位c對應“00”，相位d對應“01”，相位e對應“10”，相位f對應“11”。

根據二相位、四相位的編碼規則，在整個區域36 個路口全部編碼后，字符串的長度為51 位。其中，字符串第1～21 位對應路口C1～C21，字符串第22～51 位對應路口C22～C36。舉例說明：編碼字符串的第3、4 位解碼后分別對應路口C3、C4 的表現型；第24、25 位解碼后對應路口C23的表現型。

②初始化種群

一個種群代表所要解決的問題的潛在解集，種群中的每個抗體都是經過基因編碼的潛在解。在隨機生成初始種群之后，依據進化法則逐代搜索最優近似解。

（2）親和度評價

本文以區域路網內所有路口總的滯留車輛數為評價交通燈配時方案好壞的指標，即親和度評價規則是基于路網總滯留車輛數生成的。為了便于描述，定義一個變量Delay 來表示在單位周期內，區域路網中所有路口總的滯留車輛數。如此，本算法的親和度函數可以表示為：

其中，ti表示時間。種群中每個抗體解碼后對應區域中各個路口的交通燈狀態設置方案，根據該交通燈狀態設置方案可以計算出各個抗體對應的Delay 值。對應Delay值越小的抗體，其親和度越高，即該抗體解碼后所對應的交通燈配時方案能使區域總滯留車輛數越少。本文算法的目的就是在末代種群中選出對應的Delay值達到最小的抗體，并在該單位時間內，按該抗體對應的表現進行區域交通燈配時。

（3）免疫算子操作

免疫算子的詳細操作過程如本文第2章所述。

（4）解碼：基因型到表現型映射

解碼過程就是抗體由基因型到表現型的映射。在算法進化過程中，需要對種群中每個抗體進行解碼才能計算出它的親和度值。對最終得出的最優抗體也需要先經過解碼，然后才能按該抗體對應的表現型進行交通燈狀態設置。

在一段時間內，區域交通燈配時方案設計如果僅是考慮全部路口滯留車流量最少，那有一定可能性導致某些方向車流長時間得不到通行權，使等待時間超過駕駛人員的心理承受極限，從而容易發生交通事故。所以，還需要在由免疫克隆算法搜索出的最優配時方案基礎上進行改善。

在本文提出的配時方法中，對于二相位的21 個路口，要求最終的配時方案必須保證每個路口a 和b 這兩個相位都不會連續獲得通行權超過四個單位周期T；對于四相位的15 個路口，以8 T 為一個大周期，要求最終的配時方案必須保證每個路口在一個大周期內，c、d、e、f四個相位都至少有一個單位周期T獲得通行權。

4 區域交通燈配時仿真實驗

4.1 仿真交通場景設計

本文以西安市某區域包含36 個路口的路網為參考對象構建仿真交通場景；實驗時間段從15：30 到20：30，每15 秒作為一個時間單位T，可以分為1 200 個時間單位。為了便于本文配時方法的應用，對仿真交通場景進行簡化如下：

（1）不考慮車輛掉頭，車輛行駛方向只有直行、左轉和右轉這三種情況；且只考慮紅燈和綠燈，不考慮黃燈。

（2）對于四相位路口，直行、左轉、右轉分車道，可以得到路口每個方向的直行、左轉和右轉車輛數；而二相位路口，因為直行、左轉、右轉不分車道，只能得到整體車流數。為了簡化交通場景，將車輛直行、左轉、右轉的概率設為固定值，直行概率設置為0.8，右轉和左轉概率都設為0.1。

（3）在計算每個周期Delay 值時，每個路口在單位T時間內，各個方向車流的通過率是必不可少的。通過調研，設定實驗場景區域中各個路口單位時間內車輛通過率如表1所示。

表1 單位時間各路口車輛通過率表（輛·T-1）

4.2 交通流生成模型

交通流生成模型是交通控制研究領域的最基本模型，主要研究交通車輛的到達規律，從而解決交通流生成問題[19]。本文的研究重點不在于如何通過各種先進技術來獲取路網中各路口的實時車流量數據，只是想驗證提出的區域交通燈配時方法的有效性，因此采用交通流生成模型來模擬生成路網中各路口的實時車流量數據是合理的。

常見的交通流生成模型主要分為兩類：一是基于車輛到達隨機概率的離散型分布模型，二是基于車頭時距、車速等交通流特性的連續型分布模型[20]。離散型分布模型中較常用的有泊松分布、二項分布、負二項分布[21]。

泊松分布適用于對車輛到達率較低、車輛間相互影響小的交通流情況進行描述：

其中，P(x)為單位時間內到達x輛車的概率；λ為泊松分布參數，為正數。泊松分布的均值E(x)與方差D(x)均為λ，即D(x)/E(x)=1。

二項分布適用于對車輛到達率較高、車輛自由行駛機會不多的交通流情況進行描述：

其中，P(x)意義同式（3）；n、p 為二項分布參數，n 為正數，0 ＜p ＜1。二項分布的均值E(x)為np，方差D(x)為np(1-p)，即D(x)/E(x)＜1。

負二項分布適用于對車輛到達率波動大的情況進行描述：

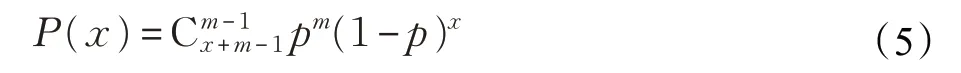
其中，P(x)意義同式（3）；m、p為負二項分布參數，m為正數，0 ＜p ＜1。負二項分布的均值E(x)為m(1-p)/p，方差D(x)為m(1-p)/p2，即D(x)/E(x)＞1。

在15：30—20：30 時段，觀測仿真參考區域內路口每單位時間T 到達車輛數據的規律，發現在15：30—16：30 和19：30—20：30 這兩個時間段內，區域路網中車流量較小，車輛間相互影響較小，每T 到達車輛數據組的均值和方差近似相等，適合用泊松分布模擬生成各路口的實時車流量數據；17：30—18：30 這一段時間，處于晚高峰時期的區域路網中車流量較大，道路擁擠，每T到達車輛數據組的方差與均值的比小于1，適合用二項分布模擬生成各路口的實時車流量數據；而在16：30—17：30、18：30—19：30 這兩段時間，前者即將到達晚高峰，后者處于晚高峰余波中，區域路網中車流量波動較大，每T到達車輛數據組的方差與均值的比大于1，適合用負二項分布模擬生成各路口的實時車流量數據。

由概率論可知，根據數據的均值和方差可以計算出分布參數，得出具體分布模型。本文仿真中采用的具體分布模型如表2所示。

表2 各時間段交通流生成模型

4.3 仿真結果分析

為了驗證本文提出的基于改進免疫克隆選擇算法的區域交通配時方法的有效性，使用Matlab編寫程序進行仿真。仿真驗證分為兩步：

（1）進行單周期性能分析，只有在單周期性能優良的前提下，多周期配時仿真實驗才有可能成功。

（2）進行五小時配時仿真實驗，分別運用本文配時方法與固定配時方法進行區域交通燈配時，對比區域路網的總滯留車輛數。

4.3.1 單周期性能分析

本文提出的區域交通燈配時方法是基于改進的免疫克隆選擇算法，而對免疫克隆選擇算法、遺傳算法等優化算法而言，從它們的進化曲線可以得出算法的收斂性能、尋優速度和優化結果等眾多信息。為驗證本文配時方法的優越性能，仿真中將本文配時方法與基于標準遺傳算法（SGA）、標準克隆選擇算法（SCS）、動態變異算子克隆選擇算法（DCS）的配時方法進行比較（動態變異算子克隆選擇算法是指算法運行中變異概率值隨迭代次數增加線性遞減）。作為對比項的三種配時方法都采用與本文第3 章中相同的編碼策略與評價指標。本文仿真實驗中的車流量數據是基于三種離散型分布模型模擬生成的，所以為了性能分析的準確性，做了三組實驗，每組實驗的車流量數據都是基于不同的分布模型，且每組實驗中包含四個對比項。

經仿真，三組單周期性能分析實驗的結果是一致的，但由于篇幅所限，僅給出由泊松分布模型生成車流量數據的仿真結果，如圖3所示。

在圖3中，（a）為基于SGA的配時方法進化曲線，（b）為基于SCS 的配時方法進化曲線，（c）為基于DCS 的配時方法進化曲線，（d）為基于本文提出的改進克隆選擇算法的配時方法進化曲線；橫坐標為迭代次數，縱坐標為每一代的最優個體對應的Delay 值。下面敘述中，四種配時方法都以基于的算法代稱。

4.3.2 五小時配時仿真分析

根據4.1 和4.2 節所述，利用交通流生成模型產生15：30—20：30這五個小時的車流量數據，再對固定配時方法、基于SGA 的配時方法、本文配時方法分別進行仿真。固定配時方法中，參考實際路網情況，將二相位路口的信號周期設置為4 T，相位序列為a 相位、b 相位，綠燈時間各為2 T；四相位路口的信號周期設置為8 T，相位序列為c相位、d 相位、e相位、f相位，綠燈時間依次為3 T、1 T、3 T、1 T。因標準遺傳算法在本文配時策略應用中運行500 代后也只能看出優化趨勢，不能收斂，所以將每個周期遺傳算法的迭代次數設定為150 來進行5 h 仿真實驗。而本文提出的改進克隆選擇算法收斂速度快且尋優效果好，5 h 仿真實驗中迭代次數設定為25即可。實驗中分別記錄固定配時方法、基于SGA 的配時方法、本文配時方法的每小時路網的總Delay值，如表3所示。

從表3 中可以看出，在五個時間段里，本文配時方法的每小時路網總Delay 值與固定配時方法相比都有了顯著減少，且減少比例都接近于40%；與基于SGA的配時方法相比，減少比例也都高于17%。從整個仿真周期看，本文配時方法的5 h 路網總Delay 值比固定配時方法減少了38.93%，比基于SGA 的配時方法減少了20.33%。

根據表3 數據，繪制了仿真結果對比圖如圖4，其中，在15：30 到20：30 這一時間段，由于晚高峰的原因，路網的每小時總滯留車輛數經歷了上升再下降的過程。但不論區域路網是處于晚高峰的擁擠狀況還是下午4時左右的流暢狀況，本文配時方法的路網總滯留車輛數相較于固定配時方法和基于SGA 的配時方法都有明顯減少。這表明本文的配時方法能顯著提高路口的通行能力，增加了區域路網的交通流暢性，驗證了本文配時方法的有效性。

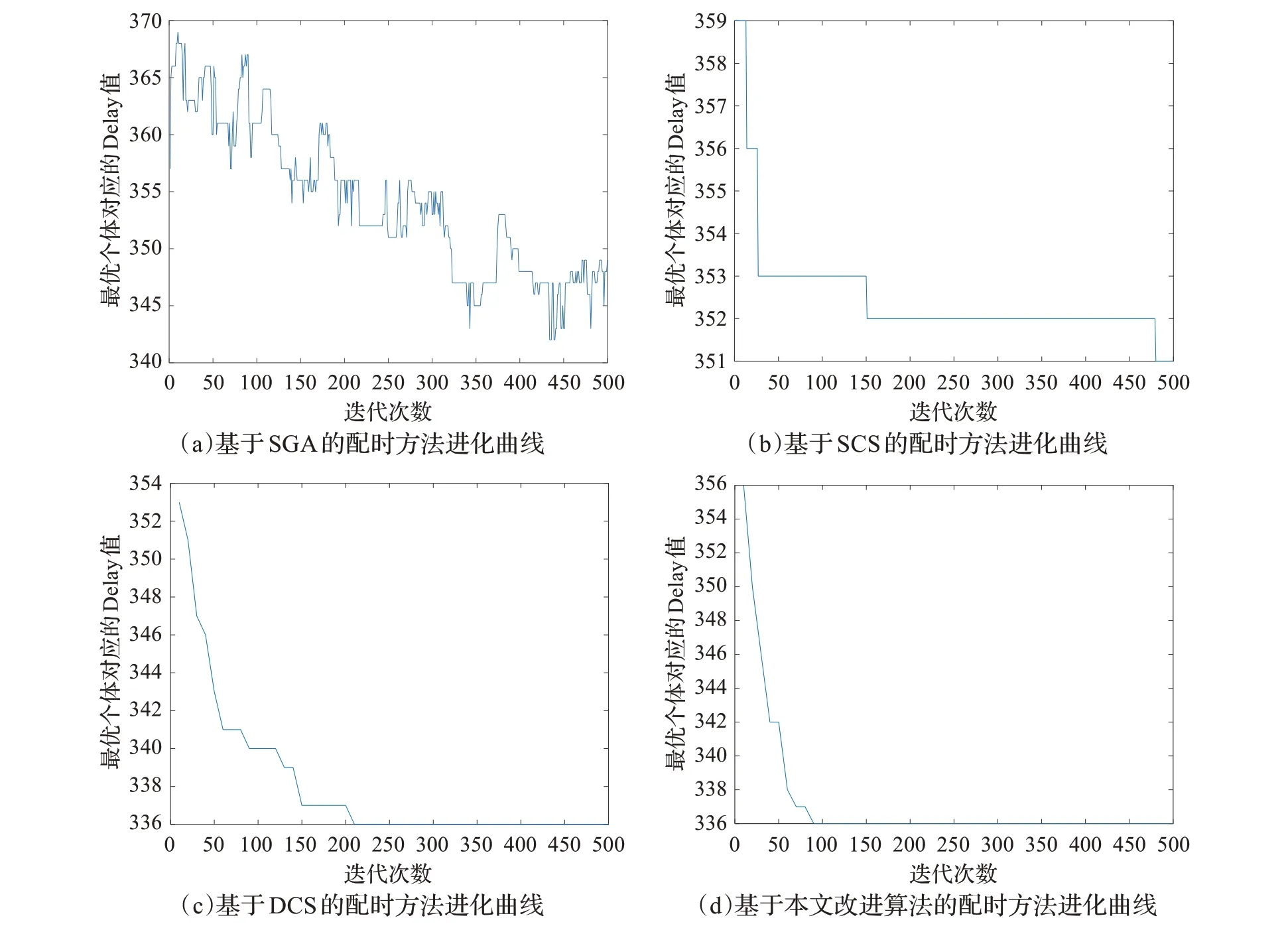
圖3 四種配時方法的進化曲線

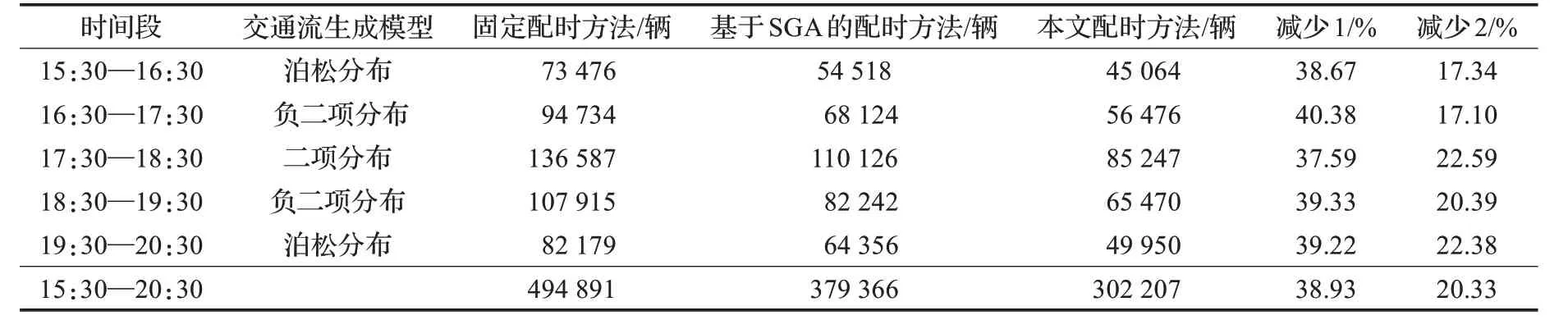
表3 三種配時方法仿真結果對比表

圖4 三種配時方法仿真結果對比圖

5 結論

（1）針對免疫克隆選擇算法收斂速度慢、易陷入局部最優等問題，本文提出了一種雙層動態變異算子，并對克隆抑制算子和種群刷新算子進行了改進。從單周期性能分析中可以看出本文的改進對克隆選擇算法性能有了較大提高。

（2）本文提出一種以區域為單位的交通燈配時方法，首先將區域內所有路口的交通燈狀態設置問題轉換成在單位時間內確定各個路口哪一個相位獲取通行權的問題，再利用免疫克隆選擇算法的全局尋優能力在每個單位時間搜索出使路網總滯留車輛數最小的交通燈配時方案。仿真結果表明本文提出的配時方法達到了優化目的，顯著減少了路網的總滯留車輛數，提升了路網的通行效率，對城市交通的緩堵保暢具有重要的現實意義。