基于改進(jìn)的小波相關(guān)性信號(hào)降噪算法?

王益艷

（1.四川文理學(xué)院智能制造學(xué)院 達(dá)州 635000）（2.達(dá)州智能制造產(chǎn)業(yè)技術(shù)研究院 達(dá)州 635000）

1 引言

在實(shí)際的計(jì)算機(jī)控制系統(tǒng)中，采樣信號(hào)不可避免地受到各種噪聲的和干擾的污染，使得由辨識(shí)采樣信號(hào)得到的系統(tǒng)模型存在偏差，而妨礙了系統(tǒng)控制精度的提高［1］。如何從這些受噪聲干擾的信號(hào)中估計(jì)得到“純凈”的信號(hào)，是建立系統(tǒng)高精度模型和實(shí)現(xiàn)高性能控制的關(guān)鍵。另一方面，在實(shí)際的工程應(yīng)用中，大多數(shù)信號(hào)可能包含著許多尖峰或突變，而且噪聲信號(hào)也并不是平穩(wěn)的白噪聲［2］。對這種信號(hào)進(jìn)行降噪處理時(shí)，傳統(tǒng)的傅里葉變換完全是在頻域中對信號(hào)進(jìn)行分析，它不能給出信號(hào)在某個(gè)時(shí)間點(diǎn)上的變化情況，因此分辨不出信號(hào)在時(shí)間軸上的任何一個(gè)突變。因此，對于非平穩(wěn)信號(hào)，在低信噪比的情況下，經(jīng)過FFT濾波處理，不但信噪比得不到較大改善，而且信號(hào)的有效信息容易被模糊掉［3］。

近年來，小波理論得到了迅速發(fā)展，由于小波具有低熵性、多分辨特性、去相關(guān)性和選基靈活性等特點(diǎn)［4］，所以它在處理非平穩(wěn)信號(hào)、去除信號(hào)噪聲等方面表現(xiàn)出強(qiáng)有力的優(yōu)越性。小波閾值降噪方法認(rèn)為對于小波系數(shù)包含有信號(hào)的重要信息，其幅值較大，但數(shù)目較少，而噪聲對應(yīng)的小波系數(shù)是一致分布的，個(gè)數(shù)較多，但幅值小。Donoho提出的基于軟硬閾值處理思想的小波域降噪技術(shù)［5～6］，它對信號(hào)先求小波系數(shù)，再對小波系數(shù)進(jìn)行閾值處理，最后通過小波反變換得到重建后的信號(hào)。但因?yàn)槠涑叨仁前炊M(jìn)制變化的，因此，在高頻段其頻率分辨率較差，而在低頻段其時(shí)間分辨率較差［7～8］。后來人們提出了很多新的改進(jìn)方法，如模極大值濾波方法，小波包分析方法等［9～11］，在一定程度上提高了降噪效果，為了充分利用小波系數(shù)直接的相關(guān)性，人們提出了相關(guān)性降噪算法［12～14］，但傳統(tǒng)相關(guān)性降噪方法容易依賴小波系數(shù)，而小波系數(shù)無平移不變性，容易出現(xiàn)偏移導(dǎo)致引起誤判［15］。基于此，本文在相關(guān)降噪算法的基礎(chǔ)上，提出了一種改進(jìn)的區(qū)域相關(guān)降噪算法。該方法對一個(gè)區(qū)域內(nèi)的小波系數(shù)進(jìn)行相關(guān)性度量，克服了傳統(tǒng)方法的不足。最后，通過對兩組非平穩(wěn)信號(hào)降噪進(jìn)行對比實(shí)驗(yàn)，結(jié)果表明，該方法對比傳統(tǒng)小波方法具有更好的降噪效果，主觀視覺效果更好，信噪比SNR、均方根誤差RMSE等性能指標(biāo)更好。

2 相關(guān)性降噪方法及其改進(jìn)

設(shè)噪聲模型為［4］

式中，x(n)為原始信號(hào)，f(n)為受噪聲干擾的信號(hào)，s(n)為高斯白噪聲，它服從分布。利用小波變換得：

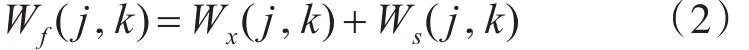
其中，Wf、Wx、Ws分別為 f、x、s對應(yīng)的小波變換系數(shù)。小波變換降噪的目的就是從有噪信號(hào)的小波系數(shù)Wf中得到原始信號(hào)的小波系數(shù)Wx的估計(jì)W?x。

由于信號(hào)小波系數(shù)的上下層之間具有強(qiáng)相關(guān)性，而噪聲沒有這種相關(guān)性。相關(guān)性降噪方法就是基于這種相關(guān)性的。下面分別給出相關(guān)性系數(shù)和歸一化相關(guān)性系數(shù)的定義。

定義1：相鄰尺度同一空間位置小波系數(shù)的相關(guān)量定義為

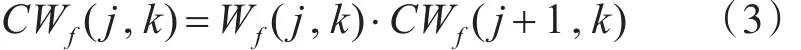
其中，CWf(j，k)稱為尺度 j上點(diǎn)k處的相關(guān)性系數(shù)。

尺度空間上的相關(guān)性使噪聲的影響大大減小，可以有效增強(qiáng)信號(hào)的細(xì)節(jié)，并且在小尺度上的作用明顯大于在大尺度上的作用。而噪聲能量主要是分布在小尺度上的，因此，這種隨尺度增大而作用強(qiáng)度減小的性質(zhì)，恰好對盡可能減小有效信息損失極為有利。

為了是相關(guān)性系數(shù)與小波系數(shù)具有可比性，進(jìn)一步定義歸一化相關(guān)性系數(shù)如下：

定義2：設(shè)

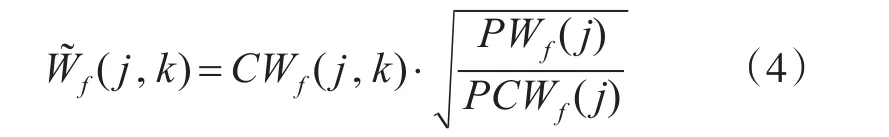
稱W?f(j，k)為歸一化相關(guān)性系數(shù)。其中，PWf(j)表示第 j層系數(shù)的能量，PCWf(j)表示第 j尺度的相關(guān)性系數(shù)能量。即

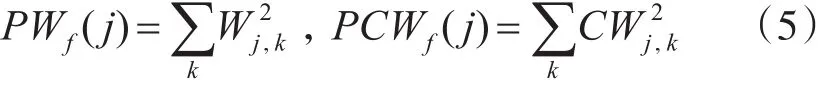
歸一化相關(guān)性系數(shù)W?f(j，k)與小波系數(shù)Wf(j，k)具有相同的能量［10］。相關(guān)性降噪的原理是比較每一層每一個(gè)位置的歸一化相關(guān)性系數(shù)，從相關(guān)性的大小判斷是信號(hào)還是噪聲控制的點(diǎn)。具體實(shí)現(xiàn)過程如下：

1）給定分解層數(shù)N，選取合適的小波函數(shù)，計(jì)算加噪信號(hào) f(n)每一層的小波系數(shù)Wf(j，k)。

2）根據(jù)式（3）～（5）計(jì)算歸一化相關(guān)性系數(shù)W?f(j，k) 。 比 較 W?f(j，k) 和 Wf(j，k) ，若W?f(j，k)≥ Wf(j，k)，則認(rèn)為大相關(guān)量對應(yīng)信號(hào)的特征 ，取 W?f(j，k)=Wf(j，k) ，置 Wf(j，k)=0 。 若W?f(j，k)＜Wf(j，k)，則認(rèn)為點(diǎn) k 處的小波系數(shù)由噪聲控制，保留Wf(j，k)，置W?f(j，k)=0 。

3）在每一個(gè)尺度上重新計(jì)算W?f(j，k)。

4）重復(fù)2）～3）的過程。

5）所取W?f(j，k)中各對應(yīng)由信號(hào)控制的點(diǎn)，而Wf(j，k)中全部為噪聲對應(yīng)的點(diǎn)。

上述相關(guān)性降噪方法對小波系數(shù)的計(jì)算依賴性很強(qiáng)，一旦在小波分解的過程中，計(jì)算結(jié)果出現(xiàn)一定偏差，則由式（3）計(jì)算出來的相關(guān)性系數(shù)Wf(j，k)不能很好的刻畫k點(diǎn)處的真實(shí)相關(guān)性，導(dǎo)致在上述算法中相關(guān)性系數(shù)與小波系數(shù)失去可比性。

改進(jìn)的辦法是采用區(qū)域相關(guān)性降噪，通過引入?yún)^(qū)域相關(guān)的概念，即考慮了點(diǎn)k處系數(shù)及其周圍的系數(shù)，改進(jìn)CWf(j，k)的計(jì)算方法。從而有效削弱了傳統(tǒng)方法因小波系數(shù)平移所帶來的不良影響。

定義 3：設(shè) CNf(j，k)=Nf(j，k)?Nf(j+1，k)，則稱CNf(j，k)為尺度 j上k點(diǎn)處的區(qū)域相關(guān)性系

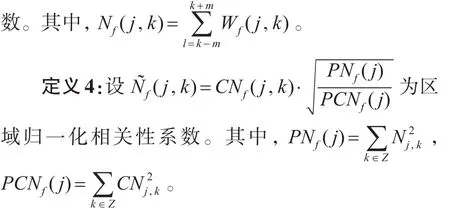
改進(jìn)的區(qū)域相關(guān)性降噪方法與傳統(tǒng)方法實(shí)現(xiàn)過程類似，只要用 CNf(j，k)和 N?f(j，k)分別替代CWf(j，k)和W?f(j，k)即可。

3 實(shí)驗(yàn)結(jié)果與分析

為驗(yàn)證本文方法的有效性，采用信噪比（SNR）、均方根誤差（RMSE）進(jìn)行客觀評(píng)價(jià)。SNR和RMSE的表達(dá)式分別為

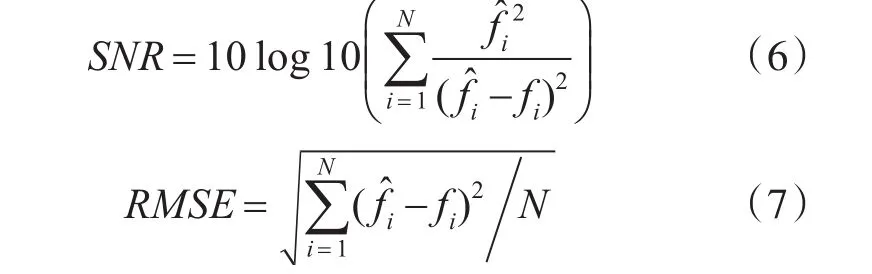
式中，f表示原始信號(hào)，f?表示恢復(fù)信號(hào)。N表示信號(hào)的長度。SNR值越大，RMSE值越小，信號(hào)降噪效果越好。

本文進(jìn)行了兩組實(shí)驗(yàn)，分別采用電網(wǎng)電壓采樣信號(hào)和醫(yī)學(xué)心電信號(hào)ECG作為測試對象，如圖1所示。

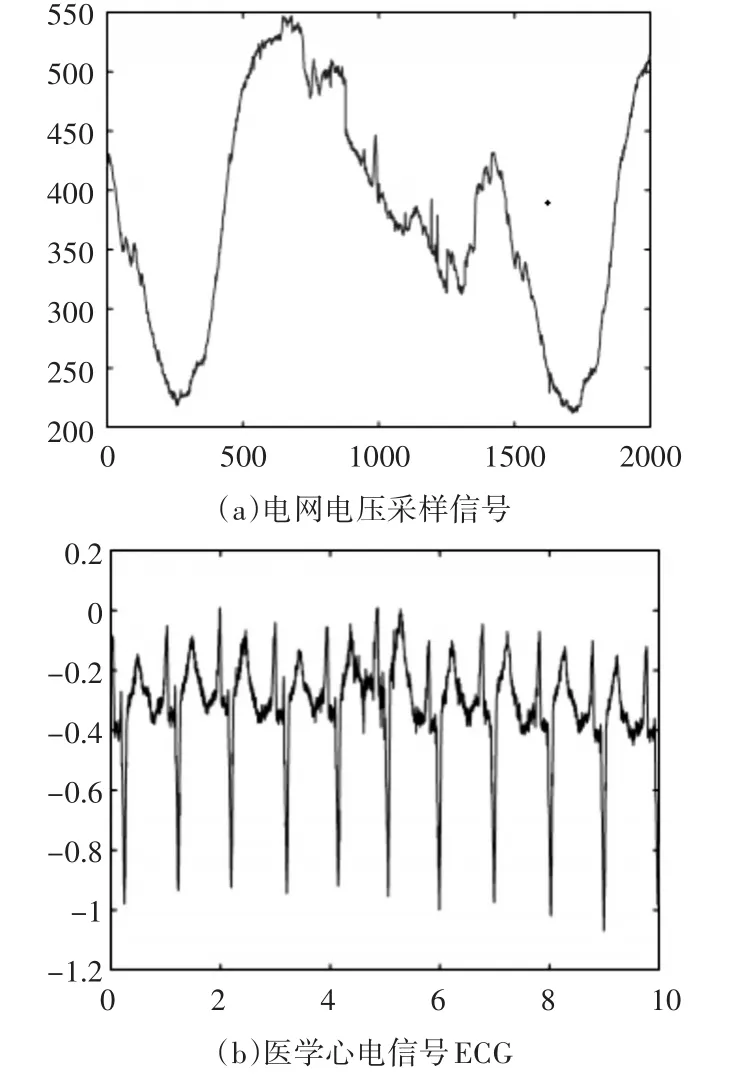
圖1 實(shí)驗(yàn)測試對象

以Matlab R2015a為測試平臺(tái)，計(jì)算機(jī)配置為：Windows7系統(tǒng)、AMD A8處理器、主頻1.60GHz、4G內(nèi)存。將本文方法與小波變換［11］、小波包變換［9］等方法進(jìn)行對比實(shí)驗(yàn)，其中小波基均為”db3”，分解層數(shù)為4層。恢復(fù)信號(hào)的主觀視覺效果如圖2和圖3所示，各降噪方法對應(yīng)的性能指標(biāo)比較如表1所示。

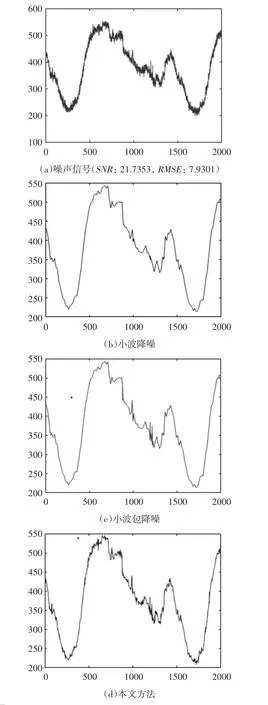
圖2 各種方法對電網(wǎng)電壓采樣信號(hào)降噪對比實(shí)驗(yàn)結(jié)果

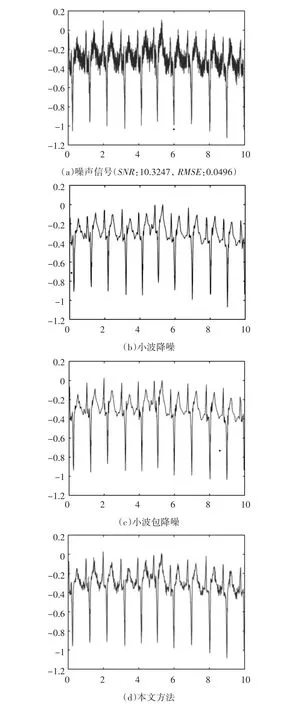
圖3 各種方法對醫(yī)學(xué)心電信號(hào)ECG降噪對比實(shí)驗(yàn)結(jié)果

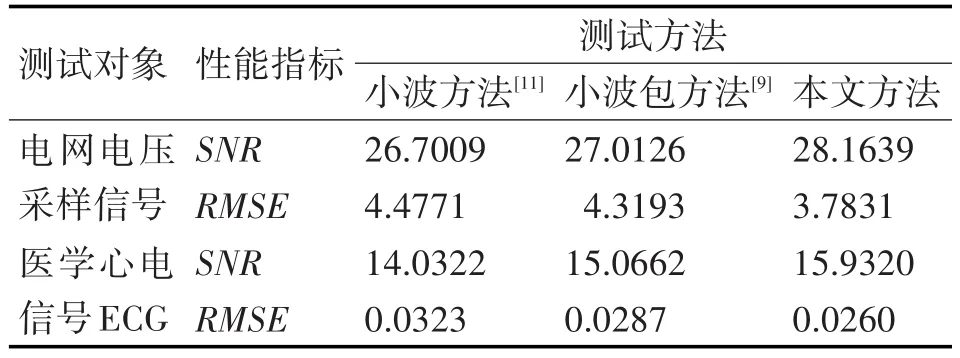
表1 各降噪方法對應(yīng)的性能指標(biāo)比較

由圖2和圖3可看出，本文方法降噪效果明顯優(yōu)于小波方法和小波包方法，對邊緣、拐點(diǎn)等細(xì)節(jié)保持更好，與原始信號(hào)更逼近。從表1中性能指標(biāo)來看，兩組測試實(shí)驗(yàn)中，本文方法對應(yīng)的SNR值都是最高，RMSE值都是最低，從側(cè)面也表明了本文方法的優(yōu)越性。

4 結(jié)語

針對非平穩(wěn)信號(hào)降噪問題，本文在相關(guān)降噪算法的基礎(chǔ)上，提出了一種基于區(qū)域信息的改進(jìn)算法。該方法對一個(gè)區(qū)域內(nèi)的小波系數(shù)進(jìn)行相關(guān)性度量，有效削弱了傳統(tǒng)方法因小波系數(shù)平移所帶來的不良影響。

通過對電網(wǎng)電壓采樣信號(hào)和醫(yī)學(xué)心電信號(hào)ECG的仿真對比實(shí)驗(yàn)，結(jié)果表明，該方法對比傳統(tǒng)小波方法具有更好的降噪視覺效果，各項(xiàng)客觀性能指標(biāo)更優(yōu)，體現(xiàn)了本文方法的有效性，