基于PSO-Elmam神經網絡對挖泥船裝艙模型的建模?

蔡 磊

（江蘇科技大學電子信息學院 鎮江 212003）

1 引言

疏浚作業在人類的社會生產過程中起到了很重要的作用，無論是保持京杭大運河的水道暢通，還是清除沉積的泥沙積石，這都離不開疏浚［1～2］。在耙吸挖泥船的疏浚作業過程中，裝艙階段是非常重要的一個階段，對于裝艙階段的建模有其必要性［3～4］。

構建此裝艙模型的主要作用是當遇到風浪較大的工作環境，水位顛簸較大難以正確讀取吃水數據時，通過神經網絡模型得到的輸出值可以起到輔助參考作用，所以構建耙吸挖泥船裝艙模型對施工作業有重要的意義。

構建裝艙模型的本質作用，是通過已知的進艙流量、進艙密度這兩個狀態輸入值，船速、耙頭對地角度、溢流桶高度這三個控制輸入值，得到裝艙體積、裝艙質量這兩個輸出值。

Elman神經網絡具有很好的非線性擬合能力，可映射復雜的非線性關系［5］。將訓練集的輸入、輸出數據進行神經網絡訓練。訓練完成之后，輸入測試集的輸入數據得到輸出數據，并與真實值進行對比［6］，從而證明用Elman神經網絡能夠對耙吸挖泥船的裝艙過程進行建模。但是，Elman神經網絡在使用梯度下降法修正權值閾值時容易陷入局部極小值［7］。可以使用粒子群算法（PSO）的全局搜索尋優能力優化Elman神經網絡的權值閾值，從而避免陷入局部極小值［8］。將優化得到的最優權值閾值作為Elman神經網絡的初始值進行神經網絡訓練。將PSO-Elman的神經網絡輸出結果與沒有優化的Elman神經網絡輸出的結果進行對比，PSO-Elman能讓建模的結果更加精確［9］。

2 Elman神經網絡

Elman神經網絡的結構共分4層，其中分別為輸入層、輸出層、隱含層和承接層。

承接層的作用是存儲上一時刻的隱含層的輸出值。隱含層有激勵函數，通常采用Sigmoid非線性函數。對于輸入層而言，其作用是信號的傳輸。輸出層的作用是線性加權。如圖1結構所示，隱含層的輸出通過承接層的延遲與存儲，承接層的輸出連接到隱含層的輸入，即隱含層的輸出自聯到輸入。這樣對歷史數據有敏感性，加強了處理動態信息的能力［10］。

Elman神經網絡結構如圖1所示。

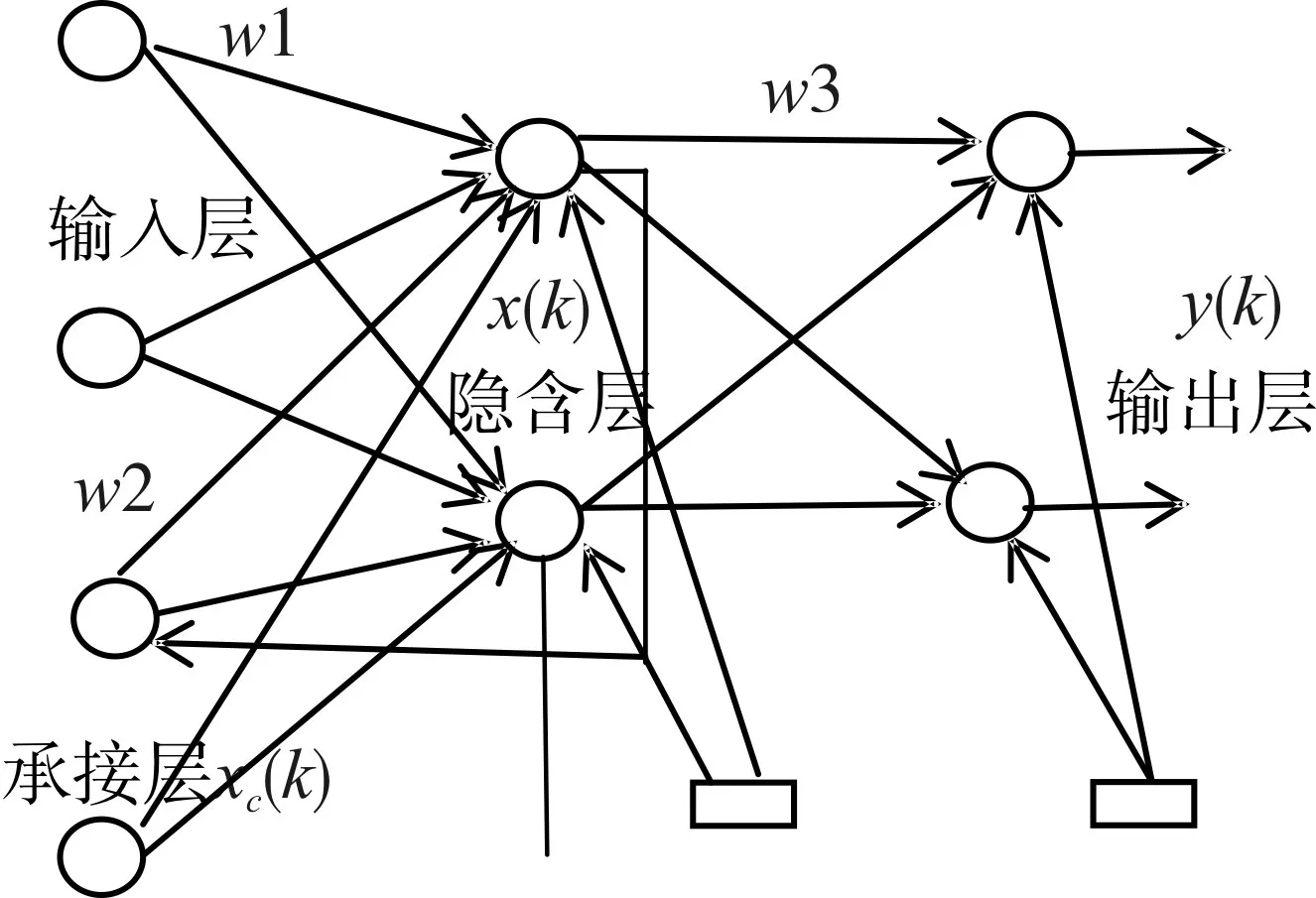
圖1 Elman神經網絡結構圖

Elman神經網絡的表達式為

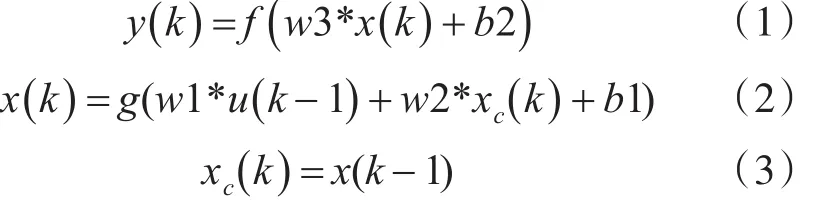
式中：k為當前時刻；x(k)為m維中間層節點單元向量；y(k)為n維神經網絡的輸出節點向量；u(k-1)為r維神經網絡的輸入向量；xc(k)為m維反饋狀態向量；w1為神經網絡輸入層到中間層的權值；w2為承接層到中間層的權值；w3為中間層到輸出層的權值；b1為神經網絡中間層的閾值；b2為輸出層的閾值；g為中間層傳遞函數，常采用Sigmoid函數；f為輸出層的傳遞函數，是中間層的輸出的線性組合。

Elman神經網絡采用梯度下降法進行權值和閾值修正，而學習的指標為［11］

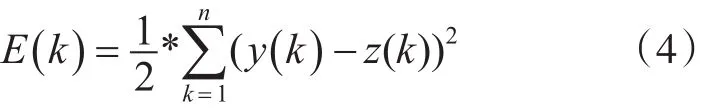
式中：y(k)為預測輸出值；z(k)為真實輸出值。

神經網絡的訓練過程是根據預測值與真實值之間的差值來不斷地修正權值、閾值，從而使誤差減小。

3 PSO優化算法應用于神經網絡

運用粒子群算法優化神經網絡的本質在于，將優化得到的權值、閾值作為神經網絡的初始權值與閾值，從而提高精確程度。

PSO-Elman神經網絡流程圖見圖2。

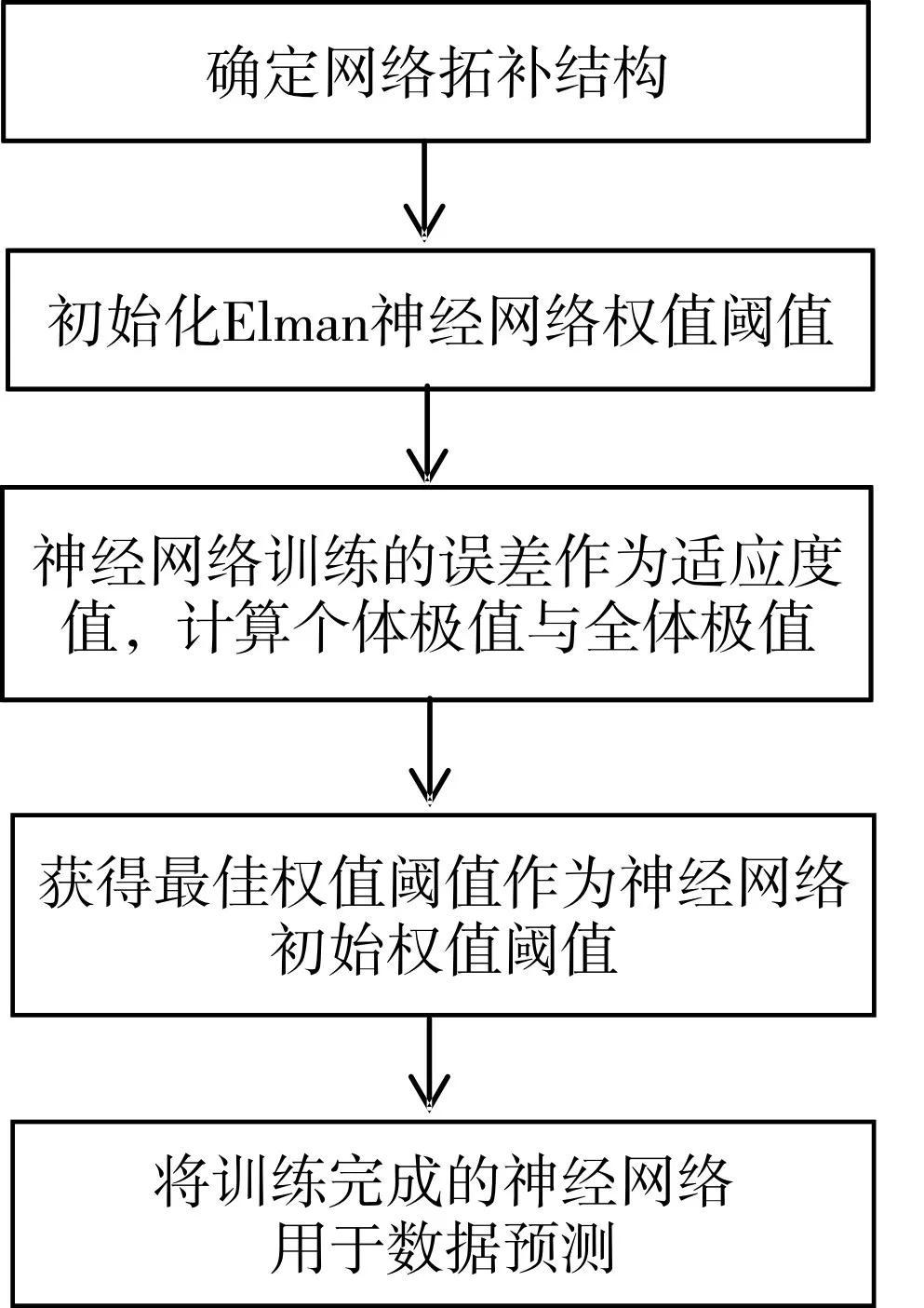
圖2 PSO-Elman神經網絡流程圖

粒子群算法是有n個粒子在d維的空間中，擁有初始的速度與位置。通過計算適應度值來尋找并更新粒子的個體極值與全體極值，根據個體極值與全體極值更新速度和位置。在空間中不斷迭代搜索，最終搜索到全局最優解［12～13］。

粒子群優化算法（PSO）的速度與位置更新公式如下［14］：

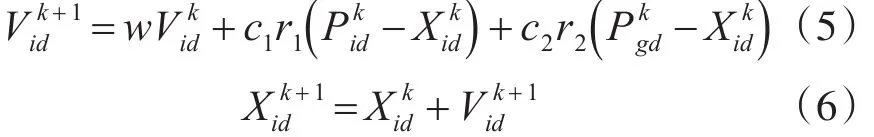
式中：與為第i個粒子在第k+1次的迭

id代中的第d維的速度與位置；為第i個粒子對于第d維的個體極值；為全體粒子中在第d維的全體極值；c1與c2為學習因子，表示粒子向優秀個體學習的能力；r1與r2為在0到1之間的隨機數；W為慣性權重，即上一迭代的粒子飛行速度慣性在當代粒子飛行速度的體現。

本文所用的W取值為［15］

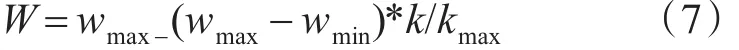
wmax為慣性權重的最大值，取值為0.9；wmin為慣性權重的最小值，取值為0.4；k為當前迭代次數；kmax為最大迭代次數。

4 PSO優化Elman神經網絡的具體順序

首先，確定神經網絡結構，根據輸入、輸出、隱含層的節點數與閾值數，確定粒子長度；

第二步，將神經網絡中的權值、閾值編碼成實數碼所表示的個體；

第三步，計算適應度值，在此處適應度的定義為：預測誤差值的絕對值和。當得到適應度值后，據此得到個體極值與群體極值；

第四步，根據極值來更新粒子的速度與位置。之后再一次計算適應度值，根據新的適應度值更新個體極值與群體極值。再根據新的個體極值與群體極值來計算粒子新的速度與位置。以此方式不斷循環，直到滿足所設定的迭代次數為止；

第五步，將滿足結束循環條件的最優權值，閾值作為神經網絡權值，閾值的初始值，進行神經網絡訓練。

從性能上考慮，相比于BP神經網絡，在神經網絡結構中增加了承接層結構，儲存了上一時刻隱含層的輸出，加強了對于動態信息的處理能力。粒子群優化Elman神經網絡，通過粒子群的全局尋優，從而緩解了神經網絡容易陷入局部極小值的問題［16］。

5 PSO-Elman神經網絡對于裝艙模型的參數選擇

首先，需要考慮的是針對挖泥船種類繁多的工況數據，選擇哪些作為控制輸入、狀態輸入與輸出。這里選擇的是將進艙密度、進艙流量作為狀態輸入值，而將船速、耙頭對地角度、溢流桶高度這三個值作為控制輸入值，將裝艙體積與裝艙質量作為輸出值，從而構建了神經網絡所需要的輸入、輸出值。

其次，確定網絡的結構與所需的參數。對于本文所指的耙吸挖泥船裝艙模型，輸入節點有5個，輸出節點有2個。隱含層節點數為11個。那么權值總共有11*5+11*2=77個，隱含層閾值11個，輸出層閾值有2個，所以粒子長度是90。種群規模設置為60，算法迭代次數設置為100，學習因子都設為1.5。Vmax設為1，Vmin設為-1。Wmax設為0.9，Wmin設為0.4。神經網絡最大訓練次數設置為1000。

6 對于裝艙質量、裝艙體積的驗證

根據長江口的一份耙吸挖泥船的工作數據，其中包含了進艙流量、進艙密度、溢流桶高度、耙頭對地角度、船速、裝艙質量、裝艙體積等工況數據。這里有4組數據，選取3組進行神經網絡的訓練，選取一組進行數據的預測比較。本文的目的在于證明PSO優化的Elman神經網絡，相比于沒優化的El?man神經網絡，對于裝艙模型的構建要更精確。所以將PSO優化的Elman神經網絡輸出的裝艙質量、裝艙體積，與未優化的Elman神經網絡的裝艙質量、裝艙體積，和工況數據中的真實裝艙質量，裝艙體積進行比較。

圖3是PSO優化的適應度曲線，可以看出，隨著迭代次數的增加，適應度值不斷降低，并趨于穩定。

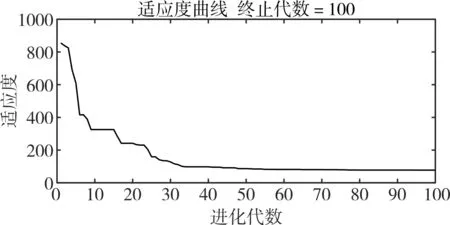
圖3 適應度曲線

圖4 、圖5分別是PSO優化的Elman神經網絡輸出的裝艙質量、裝艙體積，與未優化的Elman神經網絡的裝艙質量、裝艙體積，和真實裝艙質量、裝艙體積進行的比較曲線。可以看出，運用PSO優化的Elman神經網絡相比于未優化的Elman神經網絡，其輸出的裝艙質量、裝艙體積更加接近于真實值。

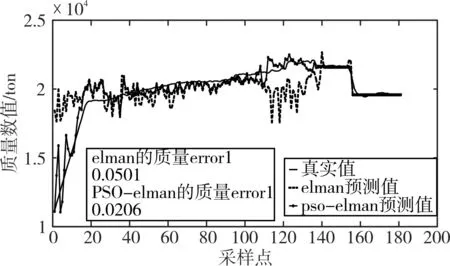
圖4 裝艙質量比較（采樣間隔30s）

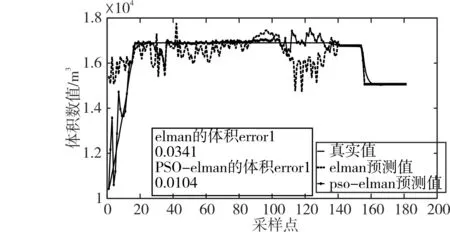
圖5 裝艙體積比較（采樣間隔30s）

圖6 、圖7則是PSO優化的Elman神經網絡輸出的裝艙質量、裝艙體積，與未優化的Elman神經網絡的裝艙質量、裝艙體積，相對于真實值的每一時刻的誤差絕對值曲線。可以看出，運用PSO優化的Elman神經網絡相比于未優化的Elman神經網絡，預測的性能更加優秀。

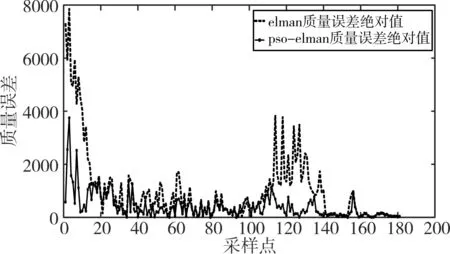
圖6 裝艙質量誤差比較（采樣間隔30s）

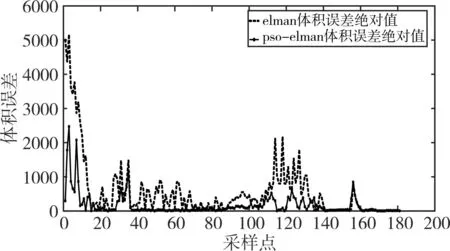
圖7 裝艙體積誤差比較（采樣間隔30s）

也可以通過比較兩種預測方法的誤差絕對值之和與真實值之和的比值，來判斷哪種方法更加優秀。

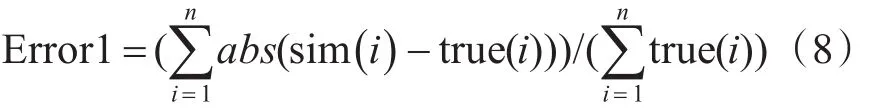
式中，sim(i)為i時刻的預測值；true(i)為i時刻的真實值；abs為求其絕對值。

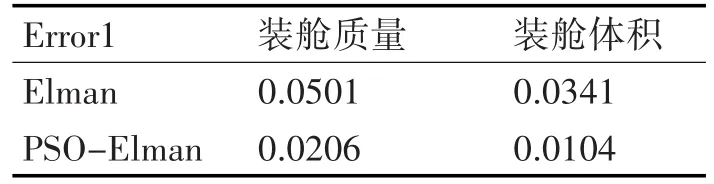
表1 2種算法的Error1數值對比

表1通過數值比較，可以看出，經過PSO優化的Elman神經網絡輸出的裝艙質量、裝艙體積的誤差要更小，精確程度更好。

7 結語

運用Elman神經網絡模型構建了耙吸挖泥船裝艙模型，實現對于裝艙質量、裝艙體積的預測。通過粒子群算法（PSO）對Elman神經網絡進行優化，減少了預測誤差，提高了精確程度，更好地構建了耙吸挖泥船的裝艙模型。