基于客流需求的列車時刻表和車底調度協同優化
林禹童,曹成鉉,柳雨彤,馮紫嫣
(北京交通大學 軌道交通控制與安全國家重點實驗室,北京 100044)
城市軌道交通為市民提供了便利的出行方式,具有運行速度穩定、運輸量大的特點。隨著交通需求量的增加,城市軌道交通也面臨著較大的運營壓力。因此,設計一個與客流需求相匹配的列車時刻表和車底調度計劃,對提高城市軌道交通的服務質量具有重要的現實意義。
在城市軌道交通列車調度問題的相關領域,國內外學者已經取得了很多研究成果,這些成果多以列車時刻表和客流需求匹配為目標。Sch?bel[1]以乘客滿意度為目標,將路線規劃、時刻表制定和列車調度三個規劃階段整合進行綜合規劃。Wang等[2]提出了以客流需求為目標的混合整數非線性規劃模型,求解和客流需求匹配的列車運行時刻表。Shi等[3]提出了以乘客滿意度為目標的模型,該模型主要討論在過飽和客流情形下,如何給出最優的列車時刻表和精確的客流控制策略。Robenek等[4]以乘客滿意度為核心建立求解最優列車時刻表的混合整數線性規劃模型。Robenek等[5]又對文獻[4]的模型進行改進,引入乘客的隨機需求要素,建立彈性需求模型。國內學者在相關研究領域也取得了一些成果。Yu等[6]和王世峰[7]提出了動態客流需求雙層規劃模型,并通過模型求解給出較優的列車時刻表和車底調度計劃。薛彤[8]應用BP(back propagation)神經網絡算法預測客流需求,對根據客流需求制定列車調度方案具有很大的參考價值。以上研究主要基于乘客需求建立模型,并進行求解,但未考慮城市軌道交通運行成本。
文獻[9-11]以列車的最小運行時間為目標建立優化模型,得出最優列車車底調度方案,并對列車運行圖的編制進行優化。周翔翔等[12]運用遺傳算法,解決了軌道交通列車系統在以成本最低為目標時的最優列車開行方案。以上研究都是以城市軌道交通運營成本最小為目標給出解決方案。
目前的研究一般都是以乘客滿意度或城市軌道交通運營成本最小為目標。本文在此基礎上,在建模時綜合考慮了乘客滿意度和城市軌道交通成本兩個要素,將兩者結合構建目標函數。在模型求解上,運用模擬退火算法,設計出列車時刻表和車底調度方案,并通過數值算例驗證模型的可行性。
1 模型建立
1.1 問題描述
在一個線狀的線路中,有m個車站,車輛段位于線路的起終點站,線路如圖1所示。列車運行路線有兩個方向,分別是方向b1和b2,兩個方向經過的車站完全相同,在線路中所有的站都需要停靠,其中,車站1為起點站,車站m為終點站。
列車運行方式為列車開始從某車輛段出發,到達某方向bi的起點站1站,然后沿方向bi出發,到達終點站m后,再進入對面的車輛段,從相反方向b3-i的起點站1站出發,執行新的運輸任務(在該問題中有兩個方向b1和b2,b1的相反方向為b2,b2的相反方向為b1,因此在一般性的描述中,用b3-i表示某方向bi的相反方向)。

圖1 城市軌道線路圖Fig.1 Urban rail transit line
1.2 模型假設
(1)兩個方向的列車在各自的線路上,互不干擾。
(2)列車在所有中間車站均停車,且停車時間為定值。
(3)車底不屬于特定的車輛段。
(4)列車到達中間站的下車率為定值。
(5)列車從某個車站發車到達另一個車站的時間為定值。
1.3 符號說明
模型中所使用的符號集合見表1,模型參數在表2中給出,模型變量見表3。

表1 符號集合

表2 模型參數Table 2 Parameters of model

表3 模型變量
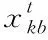
1.4 模型構建
該模型的目標為綜合目標,總共分為兩個子目標,如下:
(1)降低運營成本
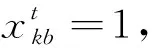
(2)降低乘客總等待時間
總乘客等待時間的計算方式,將總時間段分割成相等的離散時間段,對在每一個小的離散時間段內車站等待的乘客數進行計數,將每一個時間段內的乘客數相加,乘以離散時間段的時間單位得到總乘客等待時間。
設在方向b,車站i上的車次k和k+1的發車間隔為l,其中,
l=dk+1,i,b-dk,i,b。
(1)
單位時間段為Δt, 到達率定義為Δt內到站人數為λib,設將時間間隔分割成n個時間段,在k次列車發車后,有人數為wkib的乘客滯留在i站。其中,滯留的乘客在車次k和k+1之間的等待時間
t1=wkibl。
(2)
計算車次k和k+1次之間進站的乘客等待時間。由于乘客進站率為定值,每一個小時間段人數都增加lλib/n,則進站乘客的等待時間
(3)
在乘客達到率為定值的情形下,可以視為連續到達,則取極限
(4)
則有在該時間區間內,乘客總等待時間t總
(5)
在初始發車前的時間,滯留乘客數為0,所以乘客總等待時間為
(6)
將兩個目標乘以一定的系數求和后形成一個綜合目標,并以該目標函數最小化為最優目標。
在約束條件中,需要充分考慮要素:客流的分布情況;可調用的車底數量;列車乘客容量;最小停車間隔;客流狀態平衡的約束,其中起點站乘客下車率為0,終點站為100%。
該模型的綜合表述如下:
(7)
s.t.
(8)
(9)
(10)
(11)
(12)
(13)
(14)
(15)
(16)
(17)
(18)
(19)
(20)
(21)
(22)
(23)
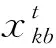
2 算法設計
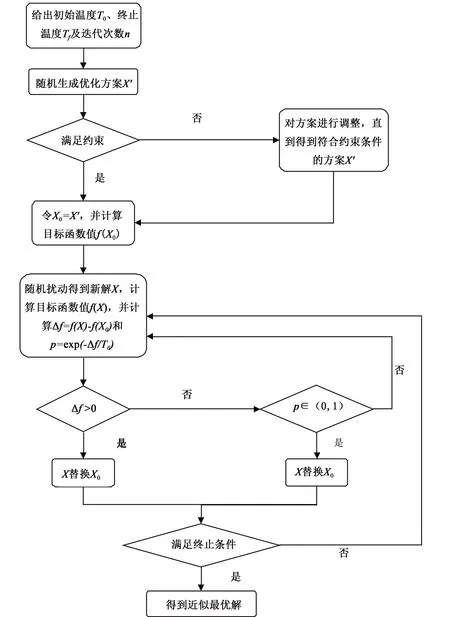
圖2 算法流程圖Fig.2 Flow chart of algorithm
在大規模問題中,找到較優列車調度方案的方法是先根據總的客流需求情況找到一個初始的運行方案,再根據每一時刻具體的客流狀況沿著一定路徑進行調整,逐漸找到較優的運行方案。由于該問題的混合整數規劃模型由0-1決策變量組成,理論上可以使用枚舉法找到最優解。但如果模型規模較大,則枚舉法并不可行,而模擬退火算法可以提高尋找最優解的效率且可有效避免陷入局部最優解的困境,因此該模型的求解應用模擬退火算法。算法流程圖如圖2所示,應用該算法的具體步驟如下:
步驟1:初始化。給出初始溫度T0、終止溫度Tf,以及迭代次數n,第一步令T=T0,n=0,轉步驟2。
步驟2:隨機生成一個優化方案X′ 。判斷此方案能否滿足約束,若滿足,則X′是可行的,令X′=X0,轉步驟3繼續迭代;若不滿足,則對未滿足約束條件的方案進行隨機調整,直到生成一個可行方案,得到初始可行解,轉至步驟3。
步驟3:對該方案進行隨機擾動,直到得到一個符合約束的新方案X,并計算該方案和原可行方案X0的目標函數的增量Δf=f(X)-f(X0),轉至步驟4。
步驟 4:若Δf<0,則令X=X0,即接受路徑X為新的路徑;若Δf≥0,計算p=exp (-Δf/T0),若p為大于(0,1)的隨機數,令X=X0,讓X成為新路徑,轉至步驟5,否則轉至步驟3。
步驟 5:進行終止條件判斷,滿足則給出可行方案,結束迭代;否則更新T0,令n=n+1轉至步驟3。
3 數值案例

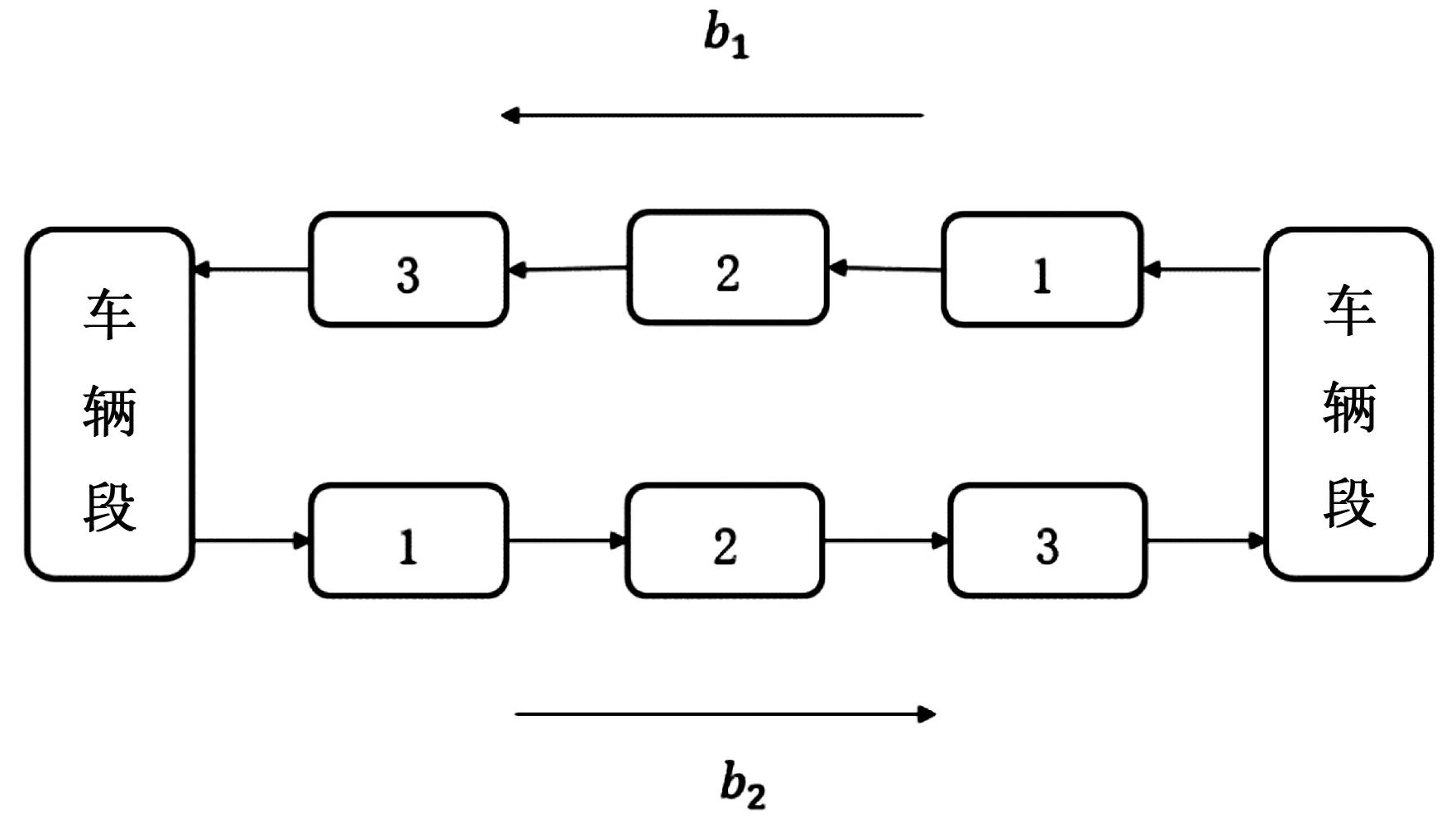
圖3 數值案例線路圖Fig.3 Transit line in numerical case

表4 算例參數
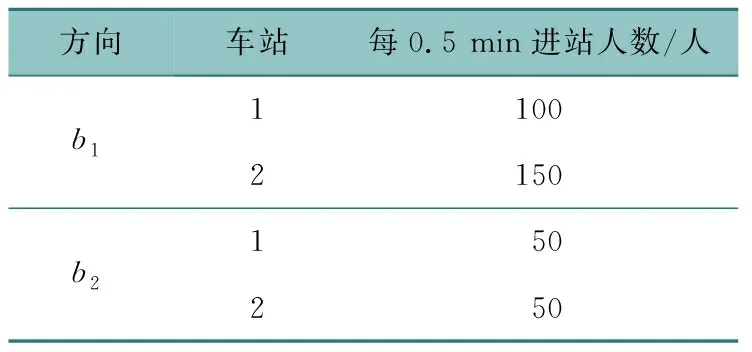
表5 乘客需求
根據表4算例參數和表5乘客需求狀況,應用模擬退火算法,得到的較優解對應的時刻表如表6所示。城市軌道交通列車運行圖如圖4所示。

表6 列車運行時刻表
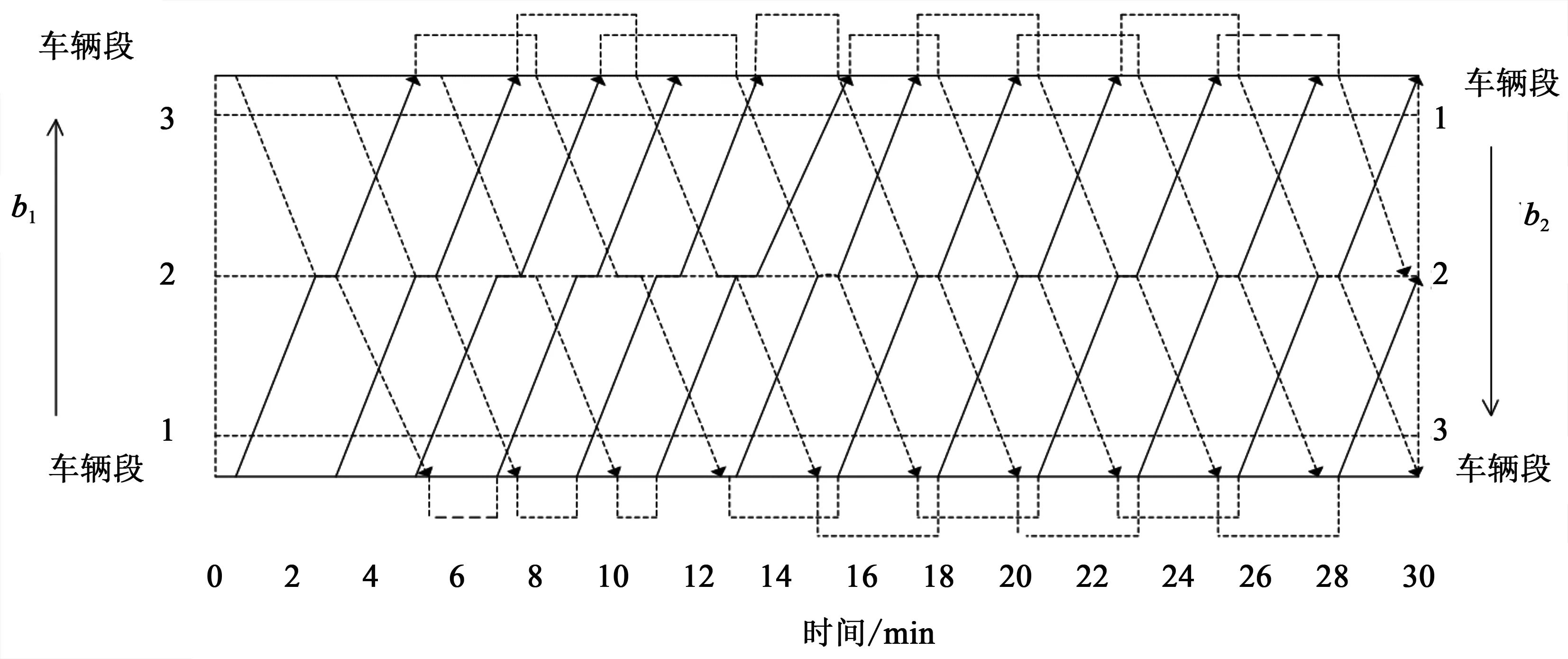
圖4 城市軌道交通列車運行圖Fig.4 Diagram of timetable planning in urban transit line
在該時間段內,由于方向b1的乘客需求大,因此和方向b2比,發車頻率較高。在目標函數中考慮降低乘客總等待時間和列車運行成本后,其發車頻率更加合理。若僅考慮降低乘客總等待時間,則成本的增加量高于乘客總等待時間的降低量后,目標函數值會增加。在建立目標函數時,綜合考慮乘客等待時間和運營成本,可得到一個和客流需求匹配,且能夠節約成本的列車運行計劃。
4 結論
本文根據乘客需求,以最小化乘客總等待時間和城市軌道交通系統運營成本為綜合目標,建立混合整數規劃模型。在模型求解時,運用模擬退火算法得到較優的列車時刻表和車底調度方案,并通過算例分析對模型進行驗證,結果證明該較優解是符合客流需求的。
本文數值算例的計算結果與預期一致。相比目標函數中僅考慮單一要素,本文考慮綜合要素后給出的列車調度方案,發車頻率保持在一個合理的范圍,且和客流需求更加匹配,不會出現列車發車頻率過高或者過低的情況。而保持一個合理的發車頻率,既可以降低乘客等待時間,提高乘客滿意度,又可以降低列車運營成本。
但是該模型是在列車停站時間及客流下車率為定值的假設下提出的,缺乏靈活性,如果乘客下車率在不同車站不同時段是變動的,則對于該優化問題中模型提出了更多的改進要求,這也是下一步的工作方向。

