數學建模在沼氣工程中的應用

宋 靜, 邱 坤

(1.成都工業職業技術學院， 成都 610213； 2.農業農村部沼氣科學研究所， 成都 610041)

1 數學建模方法簡介

1.1 回歸模型

回歸模型主要研究多個影響因素對目標函數的影響(研究變量之間的關系)。具體的做法是：首先收集大量的數據，對數據進行篩選(畫出散點圖)，剔除無效數據；對數據的統計進行分析(首先確定選擇函數公式的類型)，利用最小二乘法建立數學模型(方程組)并求解得到回歸方程的表達式，之后再對回歸模型進行顯著性檢驗(相關系數檢驗、F檢驗法、殘差分析等)；上述步驟也可采用SPSS統計軟件、MATLAB等數學、統計軟件進行。回歸模型包括：線性回歸模型(一元線性回歸模型、多元線性回歸模型)和非線性回歸模型(一元非線性回歸模型、多元非線性回歸模型)[1]。

以多元線性回歸模型為例：設因變量為y，影響因變量的因素(自變量)為x1,x2,x3,…,xn，誤差項為ε，建立方程：

y=a0+a1x1+a2x2+…+anxn+ε

(1)

式中：a0,a1,a2,…,an為模型參數

1.2 BP神經網絡

1986年，由Rumelhart和McClelland提出的多層前饋神經網絡。通過采用一種誤差反向傳播算法(BP算法)，算法的原理為：利用輸出后的得到誤差來估計輸出前面一層的誤差，再用這個誤差估計更前一層的誤差，按照此規律進行，一層層傳遞下去，從而獲得所有各層的誤差估計，我們可以根據各層的誤差來修正各層的權值[2]。通過多次迭代計算，實現實際輸出與期望輸出的差別在可以接受的誤差范圍內。BP神經網絡的學習過程包括： 1)正向傳播：樣本輸入→輸入層→各隱層→輸出層； 2)判斷是否轉入反向傳播階段； 3)誤差反傳——通過各層的誤差，修正各層的權值。下面以簡單BP神經網絡(3層)為例(見圖1)：

圖1 3層神經網絡范例圖

建模方程：

(2)

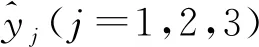
1.3 層次分析法結合模糊綜合評價

層次分析法是指對決策問題按照總目標、各層子目標進行分解；也可按影響決策問題的影響因素(元素)進行逐層分解；通過調研問卷、查閱文獻、數據分析等方式對每一層中的元素進行比較(兩兩之間的重要性進行比較)，給出重要性標度(以定量的方式)，并以矩陣的形式表示。結合數學軟件MALTAB計算出每層各元素的權重。運用層次分析法(計算出各層元素的權重)結合模糊綜合評價(對各層元素建立評判集)，通過計算得出對總體目標的定量評價[3]。

具體以對某個旅游景點的收益評價為例。

確定3個重要影響因素(例如：游客量、門票價、維護成本)，重要性標度為p1，p2，p3，特別說明：重要性標度的值越大說明越重要。以矩陣的形式給出：

2 數學建模方法在沼氣工程中的應用

引用已發表文獻中的相關數據[4]，研究3種因素(pH值，接種量,C/N)對沼氣日均產氣量的影響。發酵材料選用新鮮豬糞，接種物取自沼氣池，是以豬糞為原料富集培養的混合微生物種群，數據見表1。

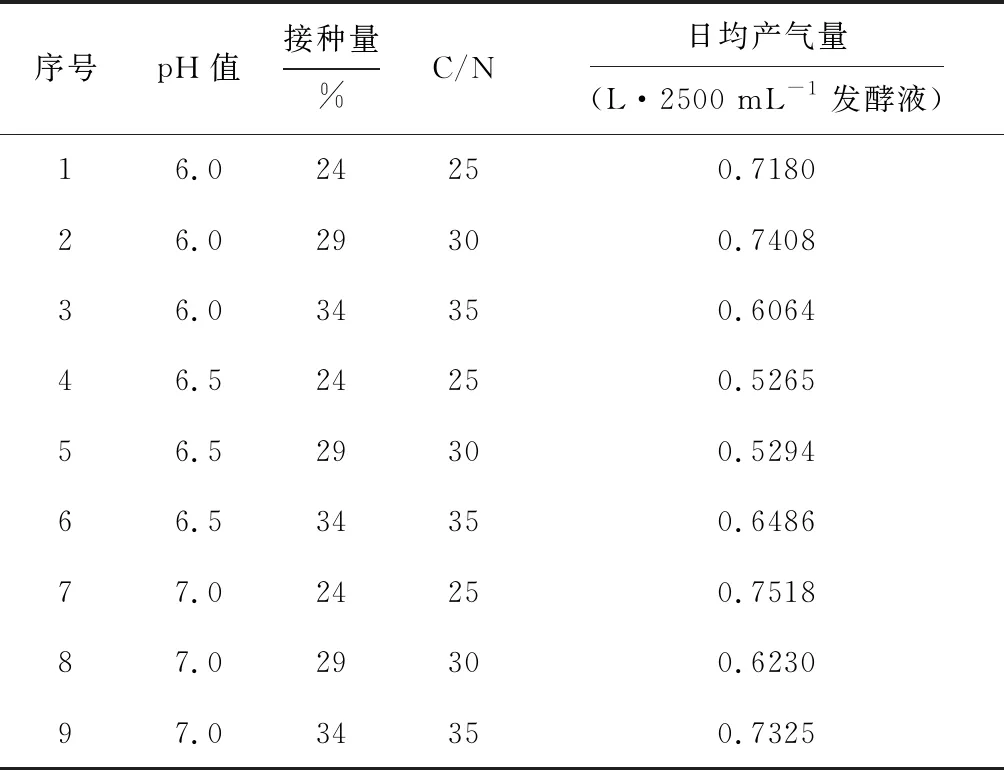
表1 3種因素對沼氣日均產氣量的影響

2.1 多元回歸模型在沼氣工程中的應用

根據表1中的數據，我們研究pH值、接種量和C/N對日均產氣量的影響，令pH值，接種量和C/N這3種因素為自變量分別為xi(i=1,2,3)，日均產氣量為因變量為y。運用線性回歸模型建立函數關系式：y=a0+a1x1+a2x2+a3x3，并用數學軟件MATLAB求解，得到：

y=0.014x1-0.5706x2+0.5703x3

(3)

特別說明，在采用此方法之前，筆者對收集的數據進行篩查，剔除掉異常點(在實際的計算過程中，筆者發現9組數據中沒有異常數據，見圖2)，再用數學軟件MATLAB編寫相關程序得到我們的結果，計算出的參數a0,a1,a2,a3均在置信區間范圍內。

MATLAB程序：

n=9;m=3;

y=[0.7180 0.7408 0.6064 0.5265 0.5294 0.6486 0.7518 0.6230 0.7325];

x1=[6.0 6.0 6.0 6.5 6.5 6.5 7.0 7.0 7.0];

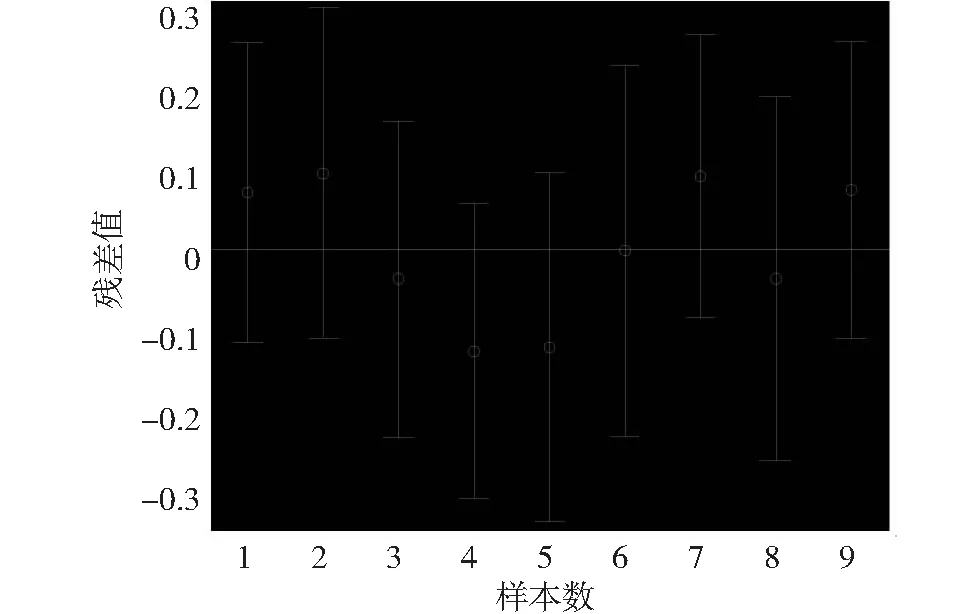
圖2 參數信度圖

x2=[24 29 34 24 29 34 24 29 34];

x3=[25 30 35 25 30 35 25 30 35];

X=[ones(n,1),x1',x2',x3'];

[b,bint,r,rint,s]=regress(y',X);

s1=sum(r.^2) /(

n-m-1);

b,bint,s,s1

rcoplot(r,rint)

2.2 BP神經網絡在沼氣工程中的應用

根據表1中的數據，可以運用BP神經網絡預測在不同條件下(pH值、接種量和C/N 3種因素確定)的日均產氣量，從而可以研究不同因素條件下對日均產氣量的影響(見表2)。

表2 不同因素條件下對日均產氣量的影響

根據表2的數據計算：當pH值=7.5，接種量=24%，C/N=25時，預測得到日均產氣量=0.6633。

MATLAB程序：

P=[6.0 6.0 6.0 6.5 6.5 6.5 7.0 7.0 7.0;24 29 34 24 29 34 24 29 34;25 30 35 25 30 35 25 30 35];

T=[0.7180 0.7408 0.6064 0.5265 0.5294 0.6486 0.7518 0.6230 0.7365];

[p1,minp,maxp,t1,mint,maxt]=premnmx(P,T);

net=newff(minmax(P),[3,2,1],{'tansig','tansig','purelin'},'trainlm');

net.trainParam.epochs=5000;

net.trainParam.goal=0.0000001;

[net,tr]=train(net,p1,t1);

a=[7.5;24;25];

a=premnmx(a);

b=sim(net,a);

c=postmnmx(b,mint,maxt);

c

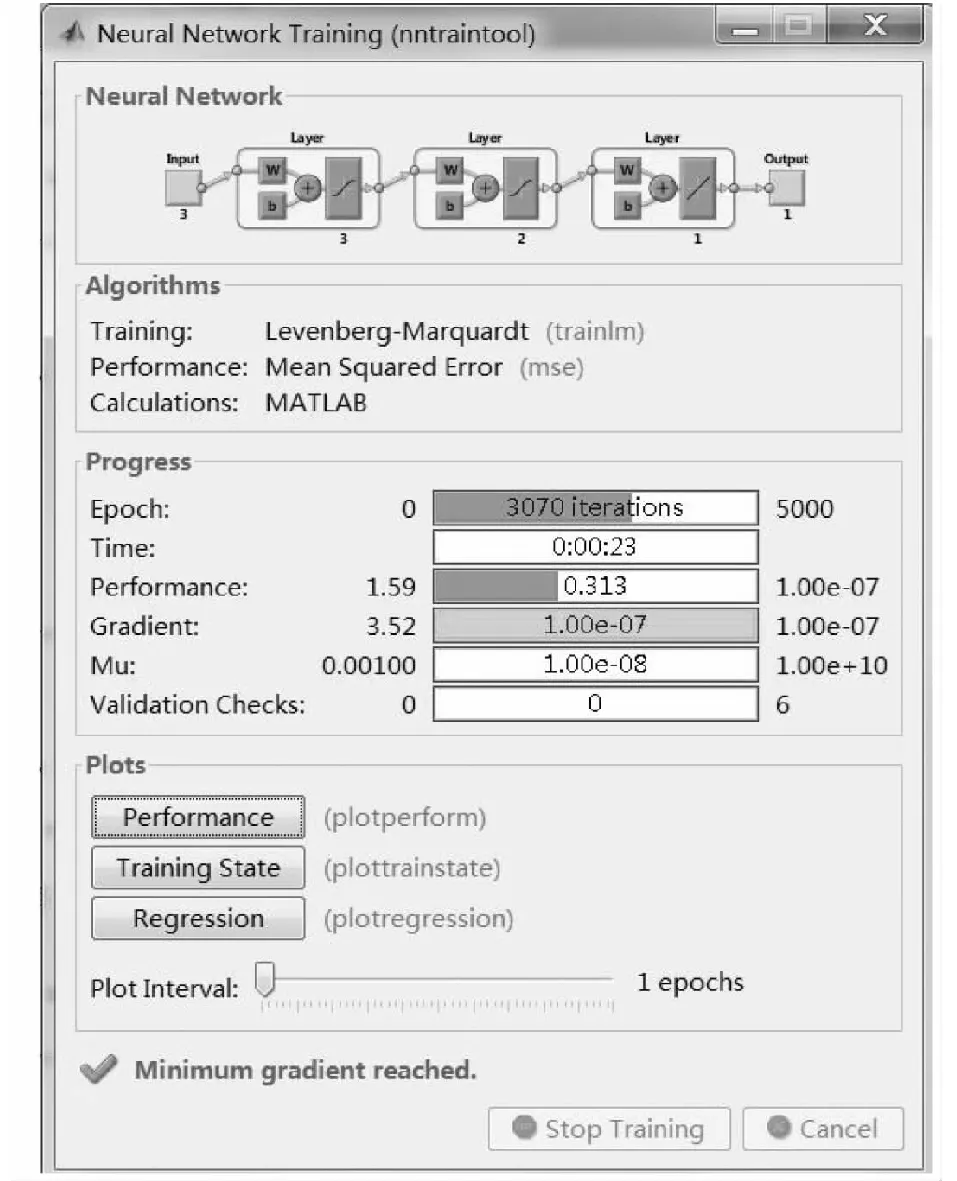
圖3 神經網絡訓練結果圖

特別說明：如圖3，運用BP神經網絡，隱藏層神經元為2，網絡迭代次數5000次，期望誤差0.00000001，在實際程序的運行過程中第3070次迭代中的計算結果已經在誤差范圍內。

2.3 層次分析法結合模糊綜合評價在沼氣工程中的應用

引用已發表文獻中的相關數據[5]，研究農戶滿意度指標體系，鑒于本文側重于介紹數學模型(層次分析法結合模糊綜合評價)在沼氣工程中的應用，因此，建立層次結構模型時僅選用部分指標。

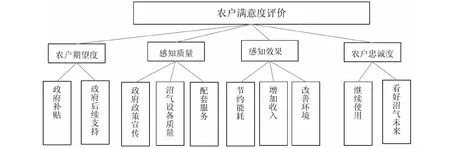
圖4 農戶對沼氣項目評價多層次結構分析圖

根據層次結構模型及參考文獻中的相關數據，建立各項指標評判集及滿意度評價表。

農戶滿意度評價集(元素集)：

W={w1-w2-w3w4}=

{農戶期望度、感知質量、感知效果、農戶忠誠度}

每一個一級指標下設立二級指標，并對每個二級指標的滿意度進行評價，詳見表3。

特別說明，在選擇表中數據時的依據更多根據文獻中各項指標的得分率。例如，文獻中提到農戶愿意繼續使用的得分率為90.4%，因此，評價“好”與“較好”兩者的比例和為90%。鑒于文獻可用數據較少，文章更側用于介紹數學模型的應用，后面3項“一般”、“較差”、“差”的比例的和滿足為10%(通過估計算得出)。此外，每項指標的比例參照上述方法估算得到。

表3 農戶滿意度評價表

對各級指標的權重進行定義，建立模糊評價矩陣，并計算矩陣的權重：

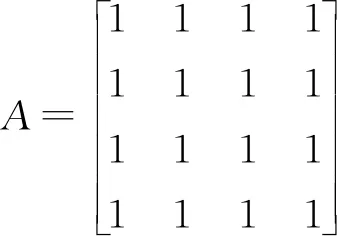
一級指標：農戶期望度、感知質量、感知效果、農戶忠誠度建立模糊評價矩陣：

計算矩陣的權重W：

這里可考慮：

計算出的權重：

即：各種因素(同層次)的重要性均是一樣的。

對于某些實際問題，特別是在各因素權重不同時，也可采用MATLAB程序實現，通過運行相關程序，輸入權重矩陣，即可計算出各因素的權重。

MATLAB程序：

clc;

clear;

disp('請輸入判斷矩陣A');

A=input('A=');

[m,n]=size(A);

RI=[0 0 0.58 0.90 1.12 1.24 1.32 1.41 1.45 1.49 1.51];

R=rank(A);

[V,D]=eig(A);

tz=max(D);

B=max(tz);

[row, col]=find(D==B);

C=V(:,col);

CI=(B-n) /(

n-1);

CR=CI/RI(1,n);

if CR<0.10

disp('CI=');disp(CI);

disp('CR=');disp(CR);

disp('對比矩陣A通過一致性檢驗，各向量權重向量Q為：');

Q=zeros(n,1);

for i=1∶n

Q(i,1)=C(i,1)/sum(C(∶,1));

end

Q

else

disp('對比矩陣A未通過一致性檢驗，需對對比矩陣A重新構造');

end

根據表3中的相關數據，得到評價矩陣：

結合二級權重矩陣，通過計算得到二級模糊評級矩陣：

B1=W11×R11=0.31 0.62 0.07 0 0

B2=W12×R12=0.2333 0.2833 0.4 0.0833 0

B3=W13×R13=0.3 0.45 0.2367 0.0133 0

B4=W14×R14=0.3 0.46 0.2 0.025 0.015

得到R：

因此，R=W×R=[0.2858 0.4533 0.2267 0.0304 0.0037]，得到一級模糊評價矩陣。

通過上述例子可以看出，農戶對于沼氣工程的滿意度從農戶期望度、感知質量、感知效果、農戶忠誠度四個方面進行評價，28.58%認為很好，45.33%認為較好，22.67%認為一般，認為較差和很差的分別僅占3.04%和0.37%。

3 小結

數學模型的運用有助于解決沼氣工程中的許多問題。包括研究產氣量與各因素之間的關系；預測在某些已知參數條件下的沼氣工程的產氣量；對沼氣工程進行定性和定量的評價等。運用數學模型，可以讓我們的結論更具有說服力，同時，也可根據模型的一些結果反推去解決沼氣工程中出現的一些技術問題，查找理論與實際值出現差異的原因。本文主要介紹了常用的3種數學模型在沼氣工程中的應用(重點在于方法的介紹與應用)，由于選用的部分文獻提供的數據有限，部分數據根據已有數據估算得到，模型與實際結果存在一定的差異性。