數形結合思想在小學數學教學中的滲透分析

黨紅強

摘 要：在數學教學中，“數”與“形”是兩大基本要素，兩者相互獨立，但又相互統一。在開展數學教學活動時，將數形結合思想融入到數學教學中，不僅可以以直觀的形式加深學生對理論知識的理解，還可以在降低教學壓力的同時，提高課堂教學效率。本文主要從理論角度出發，著重分析在小學數學教學中數形結合的概念滲透，旨在實現小學數學教學的有效性。

關鍵詞：小學數學;數形結合;滲透方法

【中圖分類號】G【文獻標識碼】B【文章編號】1008-1216（2020）01C-0049-02

數形結合指的是“數”和“形”之間的相互關系，即在一定條件下，通過“數”和“形”的相互轉變，把抽象的數學知識和直觀的圖形相結合，用以處理問題的思想方式。數形結合屬于數學中最關鍵、最基本的思想方法，是處理很多數學問題的重要思想指導。通過數形結合可以讓“數”與“形”相統一，能夠將抽象的數學知識直觀化，對學生學習大有裨益——將很難理解的計算簡單化，讓學生了解數的計算性質;讓計算時的算式形象化，使學生在明白算理的同時掌握算法;能將煩瑣問題簡單化，在解題時提高學生的思維水平與數學素養。

一、數形結合的概念

數形結合是小學教育中較為常見的一種教學方法，從學生開始接受教育到慢慢深入學習研究其他知識，數形結合的思想已經逐漸滲透到教學工作的各個環節。特別是針對數學課程來講，就是把數理知識通過圖形生動、直觀地呈現出來。學生通過這種方法可以更好地理解數學知識，了解數理的本質，這是數形結合的根本意義。

簡單地講，數形結合的主要內涵是通過圖形，生動與直觀地展現數學知識及理論，幫助學生具體地認識與掌握數學內容，形成準確的學習認知。從目前的學習特征來說，學生針對抽象事物的認識能力還很差，教師需要通過具體的圖形來表示，并采取恰當的教學方式，幫助學生更好地認識抽象事物的具體內涵及特征。

二、小學數學課堂上滲入數形結合思想的有效途徑

從教育理念角度分析，數形結合思想在小學數學課堂中的有效應用符合新課改的基本要求，且滿足小學生數學學習的要求。在新時期，教師需要從整體上分析，了解其優勢與作用，并明確其滲透途徑。

（一）提高學生分析問題的水平

小學階段是學生學習的基礎環節，教師要引起高度關注，嚴格注意學生的學習情況。在小學階段，數學基礎打不牢，以后的學習將面臨更多無法解決的問題。而小學數學教師要認識到基礎的重要意義，聯系實際生活備好課，把數形結合思想融入到相關課件中，使學生掌握知識重點，然后有目的性地分析，促使學生提高自己的解題能力和分析水平。

例如，在教學“加減法”內容時，教師結合學生實際生活中的事情給出例題：小明與小文約好星期一跑步去學校，小明共跑了800米，小文跑了980米。已知小明家與小文家在學校的相反方向，問兩人總共跑了多少米？針對這道題的分析，可運用數形結合思想，利用圖形——線段，將學校、小文家、小明家連接起來，標注對應的數字，然后計算求和。教師指引學生自主畫圖標注，努力探討問題，找到答案。因為圖示一目了然，學生解答過程十分順利。

（二）以形助數，了數的計算性質

教學時，教師將要解決的、關于數的計算性質問題，結合圖形特點體現出來，經解讀和分析圖形，讓學生更好地了解相關性質。比如，在講解分數的基礎性質時，通過折紙的方式來證明=，講解小數的基礎性質時，采用格子圖和直尺驗證0.3=0.30。課堂上數學性質的探討依靠“形”的操作，可以幫助學生主動探索到學習規律。

（三）以形助數，更好掌握算理

計算教學應指導學生清楚算理，在掌握算理的同時知道計算技巧。數形統一是幫助學生更好掌握算理的有效途徑之一。以看得到、摸得到的實體，生動直觀的演算過程，降低理解難度，使學生迅速達到“知其然并知其所以然”的目標。

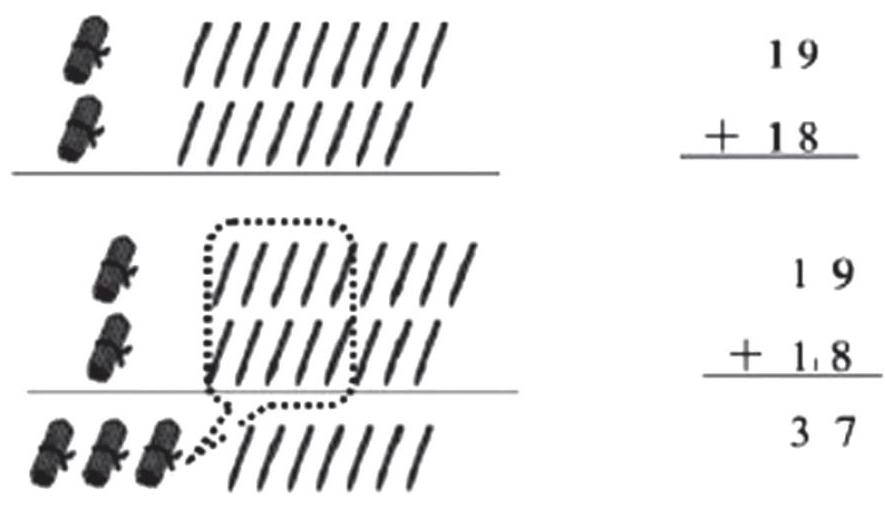
比如，在教學《兩位數加兩位數進位算法》時，了解“滿10進1”的算理為兩位數加兩位數進位加法的核心，教學中能借助小棒模仿豎式運算（見下圖），將豎式生動形象化，學生能直觀地看見運算的各個步驟，明白為何這樣算，自然就了解了“滿10進1”的算理。

再者，在教學分數乘除法的運算中，可以通過折一折、抹一抹等實踐活動掌握分數乘除法的知識點。計算教學是小學數學的關鍵內容，教學時合理采用“數形結合”方法來攻克計算的重點和難點，能體現計算方式的實質，在圖形當中融入算理。

例如，在教學“有余數除法”的內容時，教師為了讓學生理解“余數”，并知道怎樣得到“余數”，按照實際情況可以創造出這種問題情境：“現在有13根木棒，可以組成幾個三角形？同學們可以用教過的除法算式呈現出組成過程嗎？”很快便有學生舉手回答：“用13除以3。”教師先對這個學生的回答結果給予肯定與表揚，然后再繼續向全班同學問道：“有沒有同學可以根據組合的三角形講出這一除法算式的商呢？”立刻就有學生回答：“13根木棒能夠組合4個三角形，還剩1根木棒”。基于此，教師導入了“有余數除法”的有關知識點，學生不僅可以迅速理解這節課的內容，而且腦海中也有了相應的圖形，由此創建了相關運算模型。

（四）充分使用多媒體系統

多媒體系統是信息化時代進步的重要產物，其被廣泛運用于教學中，克服了以往教學受時空、地區的制約，能清楚地呈現圖片，而且，針對圖片的動態處理也可以滿足小學教學的要求。比如，通過慢放認識事物的來龍去脈，還可以縮放、旋轉、變化等，這些設計，多媒體系統都能夠滿足課堂上所要的效果，但這在現實生活中無法順利完成的。動態特點滿足學生好動的個性特征，調動了他們的好奇心，使學生喜歡課堂，改變了以往課堂單調、枯燥的情況，提高了教學效率。因此，在數形關系比較復雜時，可以利用多媒體系統來優化教學活動。

（五）以數助形，拓展思維

“形”具備形象化、直觀化等特點，但也有一定的粗略性、復雜性以及難以表達的缺點。唯有以簡單的數學描述、模式化的模型突出“形”的特征，才能更好地突出數學抽象化和形式化的價值，讓學生更好地掌握“形”的特征。

對于圖形的了解，應用數學語言進行深化。如“直線”內容的教學，因為在生活中不能找出原形，畫出來也僅僅是線段，但輔助數學語言的“直觀”“無限”以及“延展”等特點，就可以很好地創建相關表象。再者，教學“長方形”知識時，學生從圖形上感知得到僅僅是“長長的”“方方的”，唯有通過數學語言體現其特點——有四個角，均是直角;有四條邊，對邊相同，對長方形的了解才會更加深入。

幾何圖形的長度、面積、體積運算公式的歸納均是學生對形體直觀感知的深化。比如，對于正方形大小理念的形成由定性到定量，由直觀對比到數方格，由擺小長方形到找到面積和長寬之間的關系，最后得到面積求解公式，是讓學生從更深層面了解正方形。

如圖形特征，對幾何圖形性質的認識，有時需要通過運算才可得到準確結果。如周長相同的梯形、正方形、長方形以及圓形，哪一面積最大，哪一面積最小？依據直觀很難判定，但通過具體計算，結果不辨而明。

三、結束語

綜上所述，數形結合可以不失時機地為學生提供具體的形象資料，能夠將抽象的數量知識具體化，將無形的答題過程形象化，促使數學學習更加有趣。在教學中巧妙地滲透、使用數形結合概念，不僅可以為小學數學課程提供廣闊天地，還可以為學生的長期學習與長遠發展打下良好的基礎。

參考文獻：

[1]李丕峰.小學數學教學中數形結合思想的有效滲透分析[J].中國校外教育，2018，（34）.

[2]王友蓮.“數形結合”思想在小學數學教學中的應用分析[J].中國校外教育，2018，（33）.

[3]郝廣磊，徐杰.數形結合思想在小學數學教學中的實踐運用分析[J].中國校外教育，2018，（31）.

[4]江忠.巧用數形結合? 優化小學數學教學[J].教育與教學研究，2018，（1）.

[5]許娟.數形結合思想在小學數學教學中的應用探究[J].內蒙古教育（職教版），2016，（12）.

[6]張進錄.小學數學教學中數形結合思想的滲透分析[J].西部素質教育，2016，（2）.

[7]李文玲.“數形結合”思想在小學數學教學中的應用分析[J].西部素質教育，2016，（1）.