基于磨耗定量的地鐵曲線鋼軌波磨發展機理研究

鄭靈霞， 堯輝明

(1 上海工程技術大學 城市軌道交通學院， 上海 201620； 2 同濟大學 鐵道與城市軌道交通研究院， 上海 201804)

0 引 言

從二十世紀六十年代開始，中國鐵路上逐漸出現一種波浪形的磨耗，簡稱波磨。波磨不僅在鋼軌上產生劇烈的磨耗，而且會對鐵路周邊的環境造成噪聲污染，對車輛軌道零部件的壽命、乘坐舒適度以及行車安全性都會有一定影響。所以，研究波磨的形成及其發展是有必要的。

由于運行線路狀態以及車輛參數的不同,各國學者們所提出的波磨形成機理也不盡相同，關于波磨成因始終沒有一個成熟統一的說法。近年來，由于地鐵客流量變化大、線路小半徑曲線較多，加之站間距短導致的車輛啟動與制動頻繁，波磨在地鐵上也屢見不鮮。一些小半徑曲線線路從緩和曲線至圓曲線，甚至出現了逐漸增加的嚴重波磨。所以本文針對小半徑曲線上的波磨形成之后的發展機理進行研究，并基于波磨的形成機理為輪軌之間的蠕滑導致的粘滑振動的假設，建立一個鋼軌型面磨耗量的計算模型，模型考慮輪軌動力學、輪軌接觸分析以及材料磨損計算三個部分，以進行對波磨發展機理的磨耗定量驗證。

1 波磨形成與發展機理

鋼軌波磨作為世界性難題，近百年來，各國的學者們對波磨的成因、危害和防治措施進行了不少研究，仍沒有獲得徹底消除波磨的解決辦法。Grassie等人[1]將波磨形成機理概括成2個特征：固定波長機理和磨損機理，并總結了波磨的形成機理，如圖1所示。Hempelmann等人[2-3]認為輪軌結構反共振的高接觸力為鋼軌波磨的成因。Suda等人[4-5]對塑流型波磨進行了研究，研究認為輪軌自激振動為波磨的形成機理。范欽海[6-7]則基于輪軌之間的粘滑振動提出波磨的波磨成因理論，對輪軌間的磨耗功進行了模擬研究。

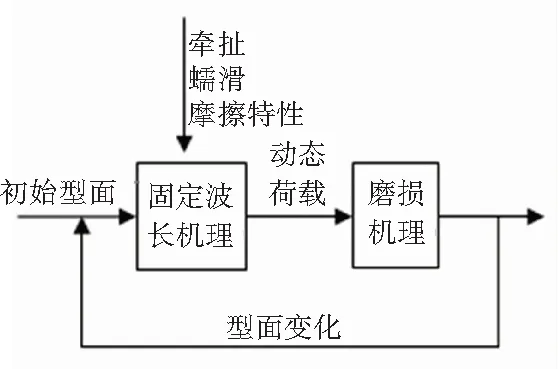
圖1 波磨形成機理

上述學者們所闡述的波磨成因雖然不盡相同，但其中大多都認同Grassie等人[1]的分類方法，即波磨的形成是輪軌動力學和接觸力學的循環反饋過程，且同時伴隨鋼軌的長期磨損。從輪軌的接觸斑上窺探的輪軌動力學和接觸力學則如圖2所示，接觸斑縱向上的法向壓力會導致輪軌之間的塑性變形，而切向力會導致輪軌之間的蠕滑，并將接觸斑劃分為粘著區和滑動區。當軌道車輛通過小曲率半徑軌道或由于加速和制動過程產生較大的縱向力情況下,接觸斑內的滑動區域逐步擴大, 最后整個接觸斑全為滑動區。在輪軌狀態變為全滑動時，輪軌間輕微的顫動將會導致粘滑振動的發生。

圖2 輪軌接觸斑范圍內的受力情況

Matsumoto等人[8]的論文中詳細描述了粘滑振動的發生過程。輪軌之間的接觸部分在輪軌間沒有振蕩的情況下，蠕滑力和蠕滑率之間的關系如圖3(a)所示，在蠕滑率—蠕滑力關系曲線上存在一個負斜率段，在負斜率段，微弱的激擾將會使車輪載荷發生振蕩。圖3(b)則為輪載振蕩時，蠕滑力在FH和FL之間的變化，曲線②表示是的負載最大值時蠕滑力特性，曲線③是負載最小值時蠕滑力特性。車輪負載振動時，在車輪負載降低過程中，車輪開始產生滑動，通過曲線上的B點，然后通過慣性達到蠕滑率最大值點C，當車輪負載回復到平均值時，車輪與鋼軌又開始處于粘著情況，蠕滑率開始突然降低，達到車輪負載最大值點D，因此輪軌間產生了A-B-C-D的這樣一個循環，即輪軌間接觸斑在粘著區和滑動區的交替過程。

(a) 無振蕩時 (b) 振蕩時

因為輪軌之間的磨損僅在接觸斑在滑動區時發生，則根據粘滑振動的發生過程，推測初始波磨形成時，車輪載荷振蕩導致輪軌蠕滑力振蕩，致使輪軌間出現粘滑振動，且蠕滑力振蕩幅度大處成為波磨的波谷，振蕩較小處位于波磨的波峰[9]。波磨形成之后，受慣性影響，波峰處的垂向壓力大于波谷處的垂向壓力，波峰處使得粘著狀態失效的蠕滑力就要大一點，所以高點處粘滑振動的幅度相較于低點處小。從磨耗量的角度來看，這個現象表現為波磨高點處的磨耗量要比低谷處的磨耗量小，如圖4所示，這也是波磨逐漸加深發展的原因。本文將以曲線線路上的粘滑振動為中心，建立一個仿真模型對鋼軌波浪形磨耗從磨耗量的角度進行定量研究。

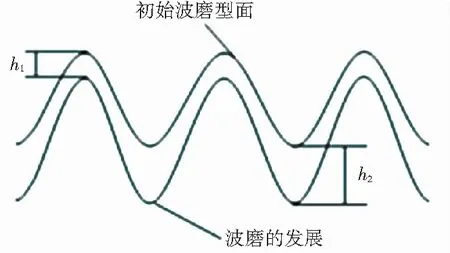
圖4 波磨發展機理

2 建立鋼軌波浪形磨耗量的仿真計算模型

2.1 仿真思路

鋼軌波浪形磨耗計算模型的建立考慮4個模塊，包括輪軌耦合動力學仿真、輪軌滾動接觸分析、材料磨損計算集成的鋼軌磨耗量計算過程，以及磨耗后鋼軌波磨型面的更新過程，具體如圖5所示。

仿真的主要思路為：線路及車輛參數輸入后，經過動力學計算，得到動態的輪軌動力學參數；通過輪軌接觸幾何分析可以得到接觸斑的形狀，輪軌接觸力學獲得接觸斑表面接觸力密度及滑動量的分布，通過一定方式疊加即可得到沿車輛行駛方向的波磨深度；由于動力學計算比較耗時，研究則進行多次磨耗計算后再進行動力學計算，設置當車輛運行達到一定次數時對鋼軌型面更新，對型面的更新結果再進行新的動力學和磨耗計算，如此反復。

圖5 鋼軌磨耗計算流程

本文主要以曲線上的粘滑振動為出發點研究，而在實際仿真中發現，車輛的一系定位剛度對粘滑振動基本無影響，整車仿真的計算也表明，二系懸掛剛度對波磨也無影響[10]，并且多名學者[11-13]的研究發現簧下質量對波磨的形成具有很大的影響，所以選用單輪對模型代替整車模型來進行鋼軌波浪形磨耗的研究，并應用hertz非彈性接觸理論來耦合輪軌之間的垂向關系，即因軌道不平順引起的垂向作用力為：

(1)

其中，G為輪軌接觸常數，δZ(t)為輪軌間的彈性壓縮量。

在輪軌接觸模型中，kalker精確理論由于計算耗時太長，一般不會用于時域仿真計算，而Vermeulen-Johnson理論在粘著區和滑動區的劃分方面略有不足，故采用kalker的簡化理論來計算輪軌接觸過程中的參數。kalker的簡化理論中接觸斑上縱、橫向蠕滑力及垂向力矩可以表示為：

(2)

其中，ξx，ξy，φ分別為接觸斑縱向、橫向、自旋蠕滑率；a，b為接觸斑的長短軸；Cij為蠕滑系數。

目前，主要用于計算車輪和鋼軌之間磨耗的計算模型有2種。一種是考慮能量耗散的角度，建立相應的磨耗功模型；另一種是材料磨損模型，其中比較典型的有Archard模型、Jendel模型和braghin模型。這些模型都是以實驗和經驗為基礎并在實際中得到較好運用的。而Archard磨損模型計算所需的參數較其他模型更容易取得，計算結果也更符合實際，故利用較為經典的Archard模型建立鋼軌波磨計算模型。

2.2 Archard磨損模型在計算鋼軌波浪形磨耗時的應用

Archard磨損模型的一般公式如下：

(3)

其中，V為鋼軌的磨損體積；P為輪軌接觸法向壓力；S為輪軌的相對滑動距離；H為材料硬度；K為磨耗系數。

為了使接觸斑上的磨耗量的計算更精確，應對接觸斑進行網格劃分。在處理時，采用kalker簡化理論以及Hains和ollerton條形理論的計算策略。在kalker簡化理論中，將輪軌接觸參數進行無量綱化處理，則接觸斑可轉換為如圖6所示的單位圓進行離散。為了研究粘滑振動對鋼軌波磨的形成的影響，需要對鋼軌縱向磨耗量的分布做清晰明了的表達，所以與條形理論的處理不同的是，平行于鋼軌型面劃分長方形帶，將每個矩形條再按照步長離散成單元格。則接觸斑上每個單元用Archard材料磨損理論計算的磨耗體積損失ΔVw(x,y)為：

圖6 接觸斑網格劃分

(4)

其中，kw(x,y)為每個離散單元上的磨耗系數。磨耗系數k的取值變化范圍與單元上滑動速度與正壓力的關系如圖7所示。圖7中的磨耗系數是在干燥清潔的條件下試驗得到的。但在實際計算時很難針對特定的滑動速度和正壓力確定特定的磨耗系數，出于對簡便計算的考慮，不同區域里的磨耗系數取中間值代替，即k1=3.5×10-2,k2=5×10-4,k3=3.5×10-3,k4=5×10-4。

圖7 磨耗系數

對于輪軌相對滑動距離Δs(x,y)，在接觸斑的粘著區內，輪軌之間不存在相對滑動，所以滑動距離為零；只有位于滑動區時，才有磨耗發生，此時滑動距離的計算公式可表示為：

(5)

其中，v(x,y)為每個單元格中心輪軌的相對滑動速度；vt為車輛行駛速度；dx為行駛方向上一個計算單元內的運動長度；v(x,y)可以由下式計算：

(6)

其中，ux(x,y)，uy(x,y)則分別為質點在縱向和橫向的彈性位移，在計算時，彈性變形產生的速度分量極小，因此計算中經常將其忽略。

通過以上計算可以得到接觸斑內每個離散單元上的磨耗體積損失ΔVw(x,y)，進而可以得到每個離散單元對應的磨耗深度Δhw(x,y)，此時需用到如下數學公式：

(7)

單個接觸斑上每個單元格上的磨耗量需要疊加到一起。為了簡化計算，對輪軌接觸狀態提出一個假設：車輪滾過一個接觸斑時，車輪與鋼軌的接觸狀態不變，包括行駛速度、正壓力、滑動速度、接觸斑面積等。由于選擇的線路較簡單，所以讓車輪重復通過一段曲線線路，以車輛通過的行程或通過這一段路程的次數作為鋼軌型面更新的依據。

3 計算結果與分析

3.1 計算條件

仿真計算中，設置單輪對在半徑為200 m的曲線軌道上運行，車輛參數使用地鐵A型車的結構參數，見表1。軌道參數取進出緩和曲線為20 m，圓曲線長為50 m，設置軌底坡為1：40，輪軌型面分別為LM車輪磨耗型踏面和60 kg鋼軌型面，車速為40 km/h，可以得到輪對在曲線上運行時，沿車輪滾動方向的磨耗深度分布。

表1 車輛參數

3.2 結果分析

圖8表示的是輪對在地鐵小半徑曲線軌道上運行一次所形成的初始波磨。左軌初始波磨波峰峰值為0.55×10-4mm，最大磨損深度為1.33×10-4mm，從初始波磨的波峰到波谷的深度約為0.78×10-4mm。右軌初始波磨波峰峰值為0.67×10-4mm，最大磨損深度為1.9×10-4mm，波深約為1.23×10-4mm。鋼軌的磨損從緩和曲線開始一直增加，至緩和曲線后段及圓曲線段形成波浪形的磨耗，到另一段緩和曲線處鋼軌磨損的周期振動逐漸平緩，直至磨損消失。輪對在經過小半徑曲線時，在緩和曲線處，蠕滑力在圖3蠕滑區，輪軌間接觸斑的滑動區增大，且磨耗僅在滑動區發生，所以鋼軌的磨耗逐漸增加但并沒有形成波磨。當蠕滑力達到圖3所示的蠕滑力最高點時，接觸斑粘著區消失，輪軌間的粘著狀態將會失效。與此同時，由于粘著狀態的失效，輪軸將釋放由于左右車輪切向蠕滑力的不同所積聚的扭轉能量。當扭轉能量下降到輪對可接受能量范圍之內時，輪軌粘著區出現，輪對又將積聚能量，粘著區增大、滑動區減小，導致磨耗量減小。即當輪對積聚能量時，磨耗量減小，能量達到飽和時，磨耗量增大。如此反復，形成周期性波動，初始波磨形成。

(a)外軌

(b)內軌

為了驗證波磨形成之后，高點的磨耗程度較低點的磨耗程度小。在仿真中，于初始波磨的基礎上加之周期0.2，波深為0.1mm的波磨，仿真結果如圖9所示。從圖9中可見磨耗量在波磨高點處周期顫振的幅度要比在低點處的小，即可以發展出，波長固定而由于波磨波峰與波谷的磨損差異導致波深不斷加深的波浪形磨耗型面。

(a)外軌

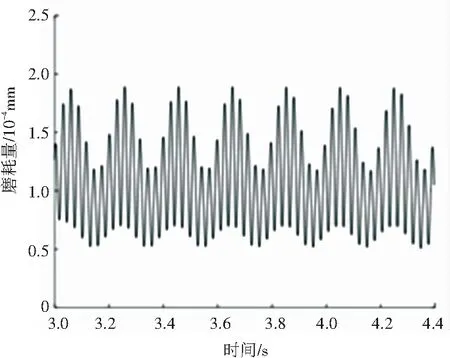
(b)內軌

圖9 添加周期為0.2，波深為0.1 mm的波磨時，行駛一次所得的磨耗量

Fig. 9 When the addition period is 0.2 and the wave depth is 0.1 mm, the abrasion amount obtained during driving once

將波磨按照行駛距離即通過曲線次數疊加，可以清楚地得到波磨的發展過程。研究后得到的5條曲線見圖10，即為輪對在圓曲線處的磨耗量，自下而上分別為輪對行駛1次、50次、100次、150次及200次的磨損量變化。行駛200次后，左軌波深為0.012 mm，右軌為0.019 mm，均約為初始波磨的154倍左右，左右軌磨耗速率大致相同。從圖10中可以明顯看出波磨波長無明顯變化，形成初始波磨后，波峰處磨耗量與波谷處磨耗量的磨損差異不斷拉大，致使波磨最大磨損深度不斷增大，從而使得波磨不斷加深發展。

(a) 外軌

(b) 內軌

4 結束語

針對地鐵小半徑曲線段鋼軌的磨耗情況，從磨耗定量的角度研究了波磨的形成與發展機理。利用Matlab/Simulink建立了一個集輪軌耦合動力學，輪軌接觸分析以及材料磨損模型為一體的鋼軌磨耗計算模型，其仿真結果和理論分析具有一致性。基于計算結果可以得出以下結論：

(1)地鐵小半徑曲線上的初始波磨由輪軌之間的粘滑振動，鋼軌磨耗從緩和曲線段至圓曲線段呈上升趨勢，在蠕滑力飽和之后的負斜率段內，鋼軌磨耗周期振蕩形成初始波磨。

(2)在波磨發展階段，初始波磨的形成使得輪軌垂向力波動，導致波磨高點處的磨耗量要比低點處的小，形成波磨波峰波谷的磨耗差異，致使波磨不斷加深，而波磨波長無明顯變化。