基于多特征融合的高魯棒性視覺SLAM改進算法

朱鳴鏑, 陳 嬋

(上海理工大學 光電信息與計算機工程學院, 上海 200093)

0 引 言

同時定位與地圖構建(SLAM)是計算機視覺和機器人領域的主流研究方法。這是指搭載有特定傳感器的主體，在沒有環境先驗信息的情況下，于運動過程中建立環境的模型，同時估計自己的運動。將相機作為唯一外部傳感器的SLAM稱為視覺SLAM。由于相機價格低，重量輕，易于裝配在其他硬件上，并且圖像包含豐富的信息，近年來視覺SLAM技術取得了很大進展[1]。

根據圖像信息如何用于位姿估計，視覺SLAM可以分為直接方法：基于特征的方法和混合方法。 本文主要討論基于特征的SLAM方法。圖像基本上是亮度和顏色的矩陣。 直接從矩陣水平考慮姿態估計是非常困難的。 因此，可以從稱為特征的圖像中選擇更多角點，這些角點在攝像機角度稍有變化后保持不變。因此，可以在每個圖像中找到相同的功能。 然后就可以基于這些特征討論姿勢估計問題。每個特征點都有一個描述符，可以定量測量與其他特征的相似性。

為了從圖像中提取角點，Harris等人[2-3]改進并提出了基于Moravec角點檢測器的Harris角點檢測算法。并且David[4]提出的SIFT角點檢測算法和Bay等人[5]提出的SURF角點檢測算法已經證明在許多應用中特別成功。一方面，視覺SLAM中的特征點應該是獨特的，對于視點和光照變化是不變的，同時對模糊和噪聲具有彈性;另一方面，檢測算法應該是計算上有效且快速的。然而，Harris、SIFT和SURF計算成本都很高，很難在視覺SLAM中實現實時速度。隨著圖像處理技術的發展，Rosten等人[6]提出了FAST特征檢測算法，大大提高了速度，并應用于PTAM[7]等一些實時SLAM應用。 Rublee等人[8]提出的ORB特征檢測算法將灰度質心法應用于FAST，使其具有旋轉不變性。 Mur-Artal等人[9-10]在2015年提出的ORB-SLAM使用ORB提取特征，這是目前最先進的視覺SLAM算法。然而，越來越多的項目正在將SLAM應用于智能手機和嵌入式設備，因此提高SLAM的速度仍然是一個亟待研究的重要問題[11]。

本文提出了一種改進版的特征點提取算法，能夠很好地應用于視覺SLAM當中。在特征點檢測中，使用多尺度AGAST角點檢測[12]算法找出具有尺度不變性的興趣點。然后，結合重心法，改進的AGAST算法可以獲得很強的魯棒性。在特征描述中，提取特征點的LATCH特征，并且這兩個特征組合形成新的二進制AGAST-LATCH特征檢測算法。

1 OARL算法

實時性能是視覺SLAM的重要前提，因此提高算法的速度始終是一項重要的研究。ORB算法本質上是FAST和BRIEF的組合。因為Mair 等人[12]提出的AGAST算法提升了FAST算法的速度與在光照變換下的魯棒性，但并未改善其對尺度變化與旋轉變換下魯棒性不高的缺陷。因此在本節中，研究提出了一種更好的特征提取過程,OARL算法(Oriented AGAST and Rotated LATCH)，就是將AGAST算法與BRIEF算法相結合。OARL算法對 AGAST 興趣點構建尺度空間并加入灰度質心法，使得AGAST算法對旋轉變換與尺度變化有著良好的魯棒性。OARL加快角點的提取，同時確保算法的性能。本文的方法是在灰度圖像上進行的。 圖1顯示了本次研究提出的OARB特征提取過程。

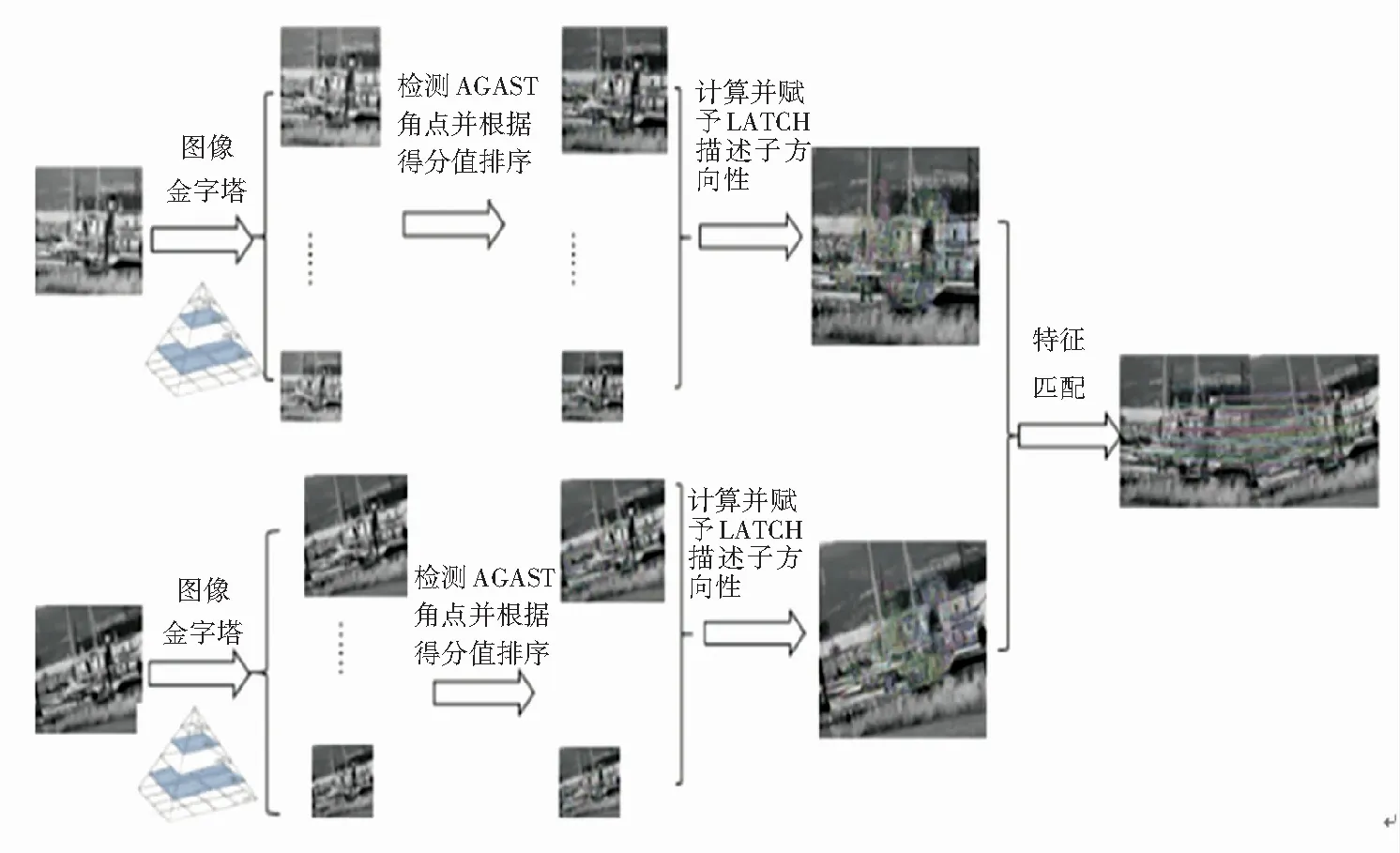
圖1 OARL特征提取過程概述

1.1 AGAST算法

FAST算法是在視覺SLAM和其他實時系統中查找特征點的首選方法。AGAST 特征檢測算法對 FAST 進行了改進，使得其相比FAST來說，運算速度更快，耗時更少，對復雜場景圖片有更好的表現。該算法檢測角點所用的判據與FAST一致，如圖2所示，FAST算法將像素“p”與Bresenham圓上的16個像素進行比較，其周圍半徑為3。 當存在亮度高于或低于中心點的連續N個像素時，像素“p”被判斷為角點。與 FAST 不同的是，AGAST 提供了一種更詳細的配置空間，采用“非較亮”與“非較暗”對原配置空間進行擴展。本文采用了以下概念:Sn→x表示為n→x的像素對于核n的狀態，分配如式( 1) 所示：

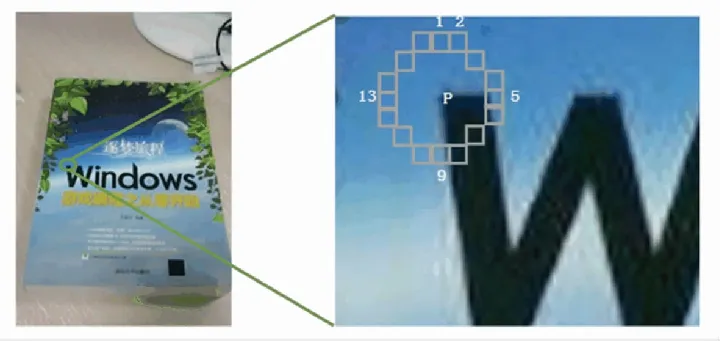
圖2 中心像素點n以及其周圍16個像素點p

(1)

其中，S'n→x是前一個狀態;I是該像素的亮度;u意味著狀態仍然未知。該結果使得二叉樹與三元樹相比時能在每個節點上單獨評估。此外配置空間大小也會增加到6N，而 616 ≈2 × 1012，所以將可能的節點N設置為16。閾值t越大，檢測到的角點越準確，計算越快，但角點數越少; 閾值t越小，檢測到的角點越多，但計算越慢。

對于一幅待檢測圖像來說，通常都具有表示均勻表面的同質化區域和(或)雜亂區域或具有紋理的結構化區域。所以，不是從訓練圖像(如FAST)學習像素配置的分布，而是首先概括學習結構化和同質區域的概率并根據該分布優化決策樹。圖像均勻的概率可以通過像素狀態與核(Ps)相似的概率來建模。“更亮”和“更暗”狀態是鏡像狀態，這意味著，例如，測試圖案上的更亮像素將在其變為中心像素時將當前核像素評估為更暗。由于這種鏡像，狀態“更亮”和“更暗”被假定具有相同的概率(Pbd)，選擇其與Ps(Ps+ 2Pbd= 1)總和為1。因此，像素配置pX的概率可用如下公式進行計算：

(2)

根據式(2)的概率分布設定，利用特定場景下的訓練集來確定概率數值，然后通過逆向歸納法構造出如圖3所示的最優二叉決策樹，在進行決策樹切換時，AGAST采用了一種自適應的解決方案。先建立2棵樹，其中一個專門用于同質化，另一個用于對圖像進行結構化；在每個決策樹的末端，對其執行基于該葉的像素配置的適當的專用樹的跳轉，如圖2所示。當像素的鄰像素發生變化時，AGAST會在2個專用樹間進行切換。葉節點的灰度越淺，則在其配置中的像素越平等。AGAST算法在生成專用樹時，離線完成的對葉節點的評估使得其在專用決策樹之間的切換沒有額外的成本。另外，左樹實現了更少的像素評估，而右樹則可以優化紋理區域。同時AST在任意場景中的適應性能也得到了改善，無須進行額外的訓練。

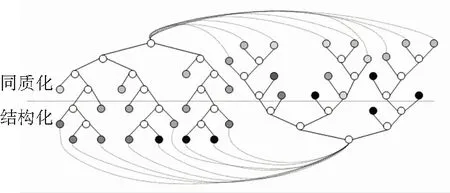
圖3 AGAST算法示意圖

Fig. 3 Schematic of the adaptive and generic accelerated segment test

1.2 改進后的AGAST算法

1.2.1 尺度不變性AGAST

在SLAM中，當相機前后移動時捕獲的相同對象將具有不同的比例，因此比例不變性對于特征檢測非常重要。由于AGAST特征檢測算法不具有尺度不變性，研究中設置了比例因子F(默認取1.2)并構建L(默認取8)層圖像金字塔，在此基礎上提取角點和計算不同尺度圖像上的描述符。這使得角點具有比例不變性。然后將AGAST9-16(圓周上共有16個像素,閾值為9)算子應用于尺度空間每一層,再記錄下候選點所在尺度空間位置,最終求出候選點及其AGAST分數V。

1.2.2 旋轉不變性

AGAST不包含特征點的方向信息，因此難以構造旋轉不變特征描述。在本節中，研究添加了一個有效計算的方向方法。本節的方法使用灰度質心[2]方法來測量角點的方向。與普通方向參數算法相比，強度質心對隨機噪聲具有更高的魯棒性。

本文采用灰度質心法來計算角點方向。首先定義一個圖像塊B的灰度矩為Mpq，數學計算公式為：

(3)

其中，I(x，y)表示此坐標處的灰度值。 本次研究中采用矩來計算圖像塊B的質心C，由其運算求得從角中心O到質心C的矢量OC，這樣就可以得到角點的方向θ，如圖4所示。 研究中給出的數學定義如下：

(4)

改進前后的算法運行效果如圖5所示。由圖5可看出，加入圖像金字塔和灰度質心法的AGAST角點面對具有尺度不變性和旋轉不變性的數據集具有了更好的魯棒性，準確率更高。

圖4 圖像塊的質心C和點的方向θ

Fig. 4 The centroid of the image block isCand the direction of the point isθ

(a) 改進前的AGAST算法

(b) 改進后的AGAST算法

1.3 LATCH算法

在先前的二進制描述符的設計中，設檢測到的圖像關鍵點為中心選取檢測窗口W，W是固定的預定尺寸的圖像塊大小，一個二進制描述子bw由T對抽樣坐標序列S={st}t=1,2,…,T={[pt,1，pt,2]}t=1,2,…,T組成，其中pt,1=(xt,1,yt,1)和pt,2=(xt,1,yt,2)定義在W坐標系，索引t既與W中的一對坐標關聯，又與高斯核σt=(σt,1,σt,2)t=1,2,…,T相關聯。對于每一抽樣對st，比較pt,1和pt,2經過光滑后的灰度，從而由式(5)來設置二進制中相應位的值，即:

(5)

其中，W(pt,1,,σt,1)和W(pt,2,σt,2)是圖像塊W中坐標pt,1和pt,2經標準差σt,1σt,2高斯濾波后的值。最終的二進制串bw由式(6)來定義：

(6)

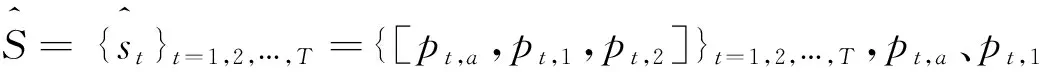
(7)

將g替換式(6)中函數f就確定了基于三元組方法的二進制串bw。

LATCH算法描述子形成過程如圖6所示。在運行時間上，LATCH描述子保持了二進制描述子的優勢，比基于直方圖描述子快好幾個數量級，在魯棒性方面，LATCH在大多數數據集上的效果優于其他二進制描述子，縮小了與基于直方圖描述子的差距[13]。

圖6 LATCH算法描述子形成過程

1.4 特征匹配

特征點匹配方法采用了漢明距離匹配法，基本原理是計算2個等長的字符串中對應位置的不同字符的個數。判斷2個向量相似程度一般有2種方式，即：距離測度法和相似性函數法。本文在漢明距離測度的基礎上再用余弦相似度作為約束，通過設定相似性的函數的閾值來去除多余的匹配點對。

1.4.1 匹配算法的改進

OARL算法匹配過程中, 如果匹配圖像局部點領域信息相近和圖像視角不同, 會引起2個不同特征點描述符的匹配程度超過同一點的特征描述符匹配程度。因此在匹配的2幅圖像中如果出現形狀相似區域, 就會產生大量誤匹配。本文使用余弦相似度進行二次匹配, 對誤匹配對進行消除。

1.4.2 向量空間余弦相似度匹配

判斷2個向量相似程度的準則一般有2種，分別是: 距離測度法和相似性函數法。其中，距離測度法是根據向量空間上存在的距離來判斷向量間的差異程度。相似性函數是用函數值的大小來表明兩向量間的差異程度。本文在漢明距離測度的基礎上再用余弦相似度作為約束,通過設定相似性函數的閾值來去除多余的匹配點對。對該方法過程可闡釋如下。

先使用漢明距離選取初步特征點對,然后再使用余弦相似度函數進一步篩選,如果2個向量的余弦值大于閾值K則保留,反之刪除 。K可以根據實驗得到,對于 2 個向量x和y,余弦相似度S(x,y)可用式(8)進行計算:

(8)

使用余弦相似度對產生縮放和旋轉、亮度對比度改變、模糊、視角變化的4類圖像進行測試,選擇平均閾值K=0. 977，測試結果見表1。

表1 測試結果

2 算法流程設計

本文提出的OARL算法設計流程如圖7所示，以實現檢測和描述的優勢互補以及快速性和魯棒性的有效結合。

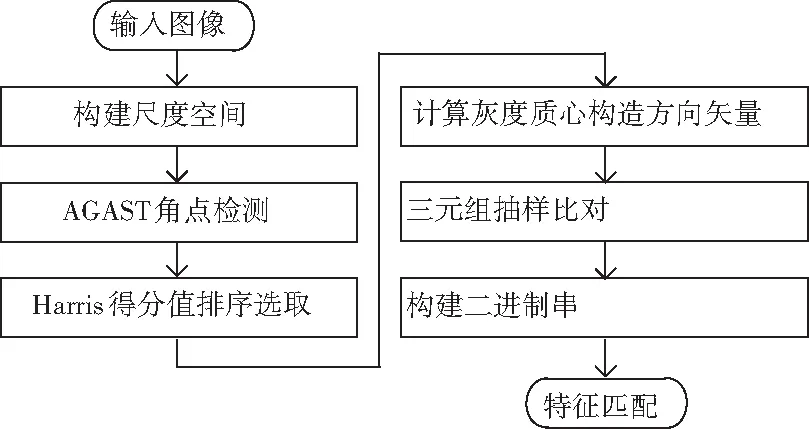
圖7 OARL算法流程圖

在多尺度AGAST角點檢測上，對輸入圖像進行圖像金字塔尺度空間的構建，而后對每一圖層進行AGAST角點檢測和尺度評判與特征的選取。在二進制描述階段，首先采用灰度質心方法對特征周圍固定大小的圖像塊進行方向補償，而后對旋轉后的圖像塊進行抽樣和三元組的選取比對，從而為特征點形成二進制描述子，為后續的特征匹配做好基礎準備工作。

3 實驗環境及分析

研究用Mikolajczyk數據集[14]作為測試用圖，以正確匹配率作為評價指標來評估OARL算法，實驗測試設備是ubuntu16.04操作系統的臺式電腦，在其上進行了所有實驗,CPU3.5 GHz, 8 GB內存,采用Microsoft Visual Studio code2018編程實現，本文使用2個性能指標來評價算法：計算時間，重復率[15]。其中，重復率中的距離閾值設定ε=1.5，映射到另一幅圖像中重疊誤差閾值設定為小于0.2。

3.1 平均計算時間

這里，將研究中的OARL算法與傳統的SIFT、SURF、ORB算法各自選擇2 000特征點進行比較，結果見表2，可以看出本文的OARL算法與ORB算法的運算時間是同一數量級的，稍快一些，仍然保持實時性，比SIFT，SURF的運算速度低好幾個數量級。

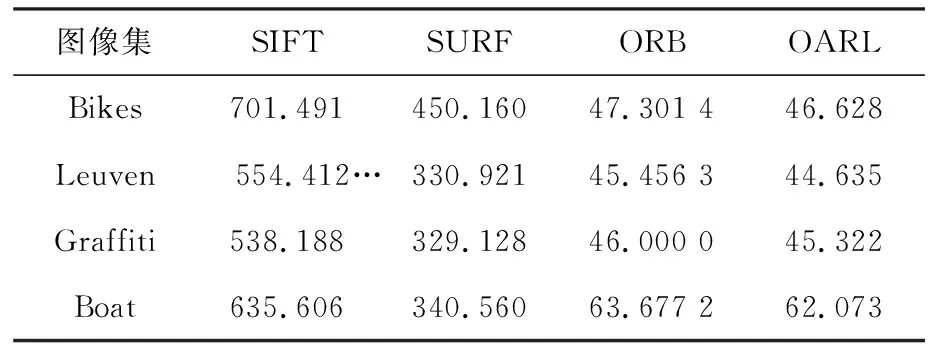
表2 各算法運算在不同數據集上的時間

3.2 匹配精度

首先，研究在Mikolajczyk的數據集中選擇了4組圖像，從圖像模糊、不同光照、不同比例和不同視角等方面評估算法的性能。仿真在4組測試圖片中的每一組上執行OARL原始方法50次。圖8、圖9和表3顯示了結果。表3中，第三列和第四列顯示從左側和右側的圖像中提取的特征點的數量。第五列顯示檢測時間。最后一列顯示了成功匹配的數量。可以看出，在模糊、亮度變化、視點變化、變焦和旋轉的情況下，本文的ORAL算法平均匹配時間與ORB算法為相同數量級，但是正確率卻平均提升了5%左右。本文的OARL算法在不同環境變化下，準確率均高于ORB算法，這主要是因為，OARL算法的三元組F范數有著良好的抗干擾性和應對局部表觀變化的能力，并且具有旋轉機制，從而使得改進算法具備較好的尺度和旋轉不變性，縮小了與傳統的SIFT和SURF算法之間在魯棒性的差距。

圖8 OARL算法在Mikolajczyk數據集上的效果

圖9 ORB算法在Mikolajczyk數據集上的效果

從圖8、圖9可以看出，與ORB算法相比，本文的OARL算法比ORB算法匹配要更加整齊，這也顯示出匹配精度的優劣，表3的結果也顯示，在相同檢測角點情況下，匹配的正確率高于主流的ORB算法和傳統的直方圖的特征點描述法，速度卻可以達到實時檢測。

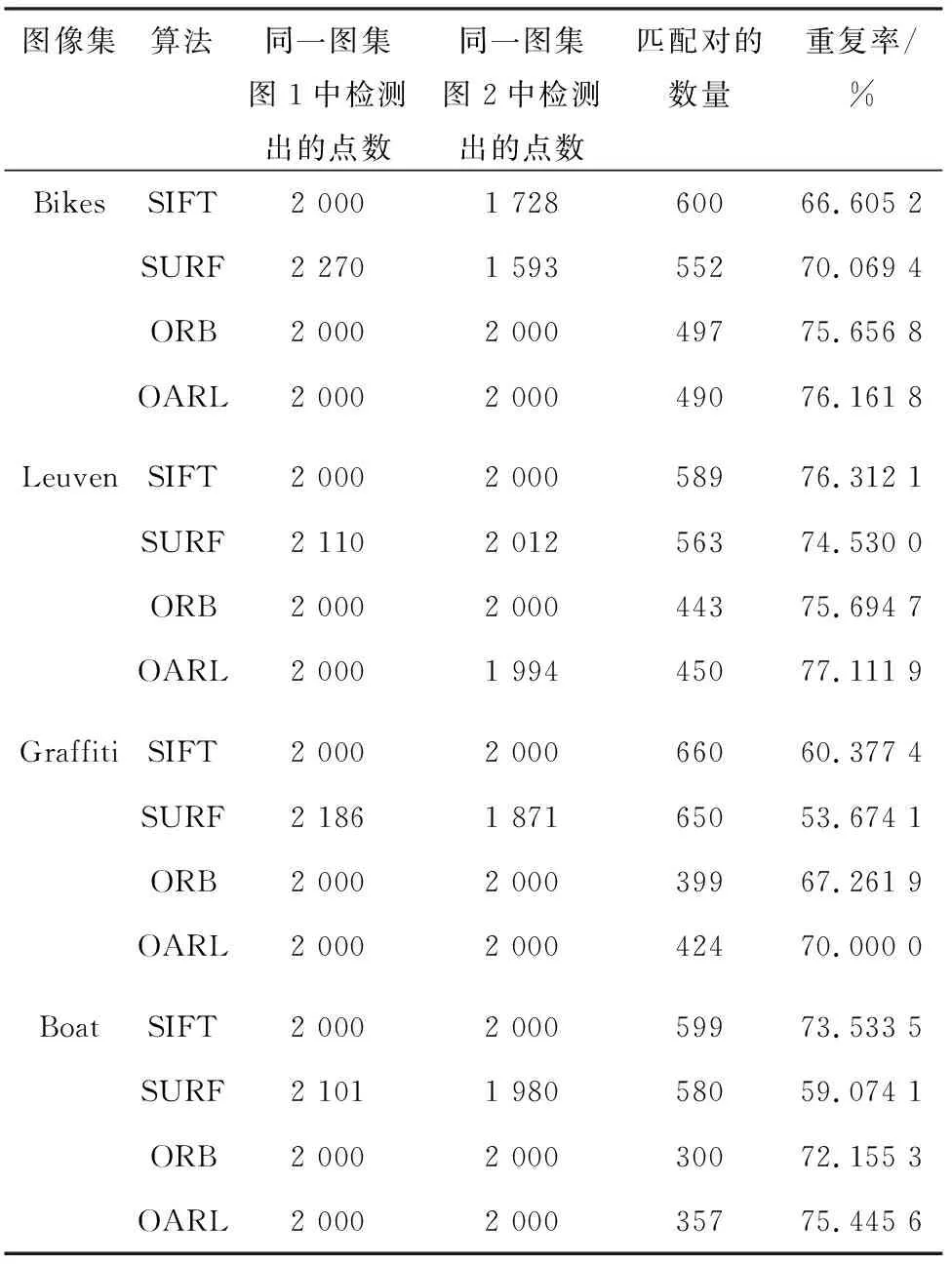
表3 各種算法在不同情況下重復率

4 結束語

本文提出了一種新的特征提取過程，稱為OARL算法，可為圖像構建一個尺度金字塔，并檢測每個金字塔層中的AGAST角點，再測量每個角點的方向。圖像集和序列的實驗結果表明，與OpenCV中使用的ORB算法相比，所提出的OARL算法將精度提高了5%以上。通過實驗可以得知，本文提出的OARL算法同時在面對旋轉、尺度變化以及亮度變化的情況下都具有良好的魯棒性，且精確度優于ORB算法,但速度卻依舊可以達到實時運算。