大型薄壁纏繞型復材殼體的振動特性研究 ①

趙雪堯，任全彬，羅志清，韓 飛,2

(1.中國航天科技集團有限公司四院四十一所 固體火箭發動機燃燒、熱結構與內流場國防科技重點實驗室，西安 710025；2.西安交通大學，西安 710049)

0 引言

復合材料具有比強度、比模量高，抗疲勞性能好等優良性能，在航空航天領域應用廣泛，其中以纏繞型復合材料結構在大型固體火箭輕量化設計中的應用效果最為顯著，使固體火箭發動機推重比、火箭射程等關鍵性能得到大幅提升。

在運輸、發射、飛行過程中，固體火箭艙段殼體將承受不同程度的振動載荷，與各向同性的金屬殼體相比，復材殼體結構振動特性的研究更為復雜。朱春艷等[1]針對全透波段非金屬夾層結構的新一代運載火箭衛星整流罩，建立了由簡化的梁、殼等單元構成有限元模型，計算了半罩在不同邊界條件下的模態特性。田旭軍等[2]為研究泡沫夾芯復合材料加筋結構在工程應用中的振聲效果，針對泡沫夾芯復合材料加筋板格結構和鋼制板格結構，開展了空氣中的振動模態對比試驗。劉建良等[3]以玻璃鋼板為設計基準，針對碳/玻混雜、橡膠格柵夾層、浮力材料格柵夾層等3種典型復合材料板方案，開展了固有頻率和振動加速度振級特性的仿真分析和模型試驗研究。黃政等[4]在ANSYS Workbench平臺中，采用ACP模塊對復合材料螺旋槳的建模進行了分析，介紹了復合材料螺旋槳的建模流程、流體計算模型和固體計算模型。尤軍峰[5]根據固體火箭發動機復合材料殼體逐層纏繞的實際工藝進行復合材料殼體細觀力學有限元計算方法研究，將計算模型簡化為1/60，較真實地建立固體火箭發動機復合材料殼體有限元分析模型，并模擬水壓試驗工況進行了有限元仿真計算。為復雜構型纏繞性復材殼體的力學仿真提供了重要參考。

本文基于復合材料層合板理論，建立某型固體火箭整流罩殼體的細觀動力學分析模型，開展隨機振動仿真及關鍵參數影響規律研究，以期為大型薄壁纏繞型復材殼體結構振動特性研究提供參考。

1 試驗原則和方法

1.1 細觀分析模型

細觀分析方法是將層合板(殼)拆分成多層材料，通過單層材料對復合材料整體進行應力、應變和失效分析的方法。與宏觀方法相比，細觀方法能對每層及層間的應力、應變和失效方式進行分析；且較于微觀分析方法，又極大地減少了節點和單元的數量。因此，細觀分析方法是目前使用較為普遍的數值計算方法[6]。

單層材料的結構如圖1所示。

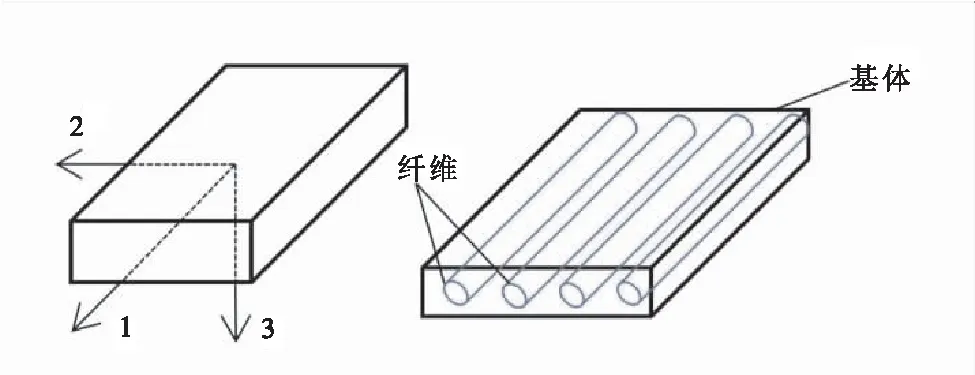
圖1 單層纖維示意圖

根據單層材料中纖維與基體的配比，可得：

(1)纖維質量分數ψfib

(1)

式中Gfib為纖維質量；Gtot為單層材料總質量；ρfib、ρmat分別為纖維密度和基體密度；Afib、Amat分別為纖維和基體的截面積。

(2)纖維體積分數φfib

(2)

式中Vfib為纖維體積；Vtot為單層材料總體積。

(3)基體質量分數ψmat

(3)

(4)纖維體積分數與基體質量分數的轉換

(4)

單層材料可看作是正交各向異性材料，其3個方向的彈性模量、剪切模量和泊松比可由E1、E2、E3、G12、G13、G23、υ12、υ13、υ23表示。這9個參數可由混合法則計算出，最常見的是Jones法則：

E1=φfib·EF1+(1-φfib)·EM

(5)

(6)

E3=E2

(7)

(8)

G13=G12

(9)

G23=φfib·GF23+(1-φfib)·GM

(10)

υ12=φfib·υF12+(1-φfib)·υM

(11)

υ13=υ12

(12)

υ23=φfib·υF23+(1-φfib)·υM

(13)

1.2 層合板等效理論

層合板是由多個單層板粘結而成的，但由于各單層板很薄，層合板的總厚度與其他尺寸相比仍然小得多，在整體上可把層合板視作一塊非均質的各向異性薄板。

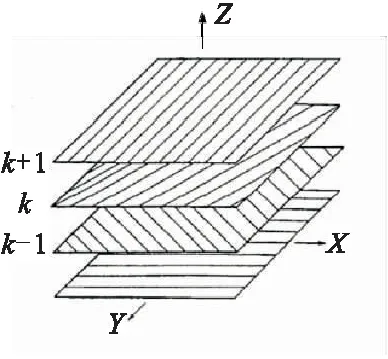
圖2 層合板鋪層示意圖

各單層板的力學性能和厚度以及其鋪層方向和序列決定了整個層合版的性能。由于層合板相當于一塊非均質的各向異性薄板，與均質材料結構不同，故須立足于每一單層對層合版進行分析，其基本假設為[7]：

(1)層間變形一致假設；

(2)直法線不變假設；

(3)在厚度方向上的正應力σz=0假設；

(4)單層平面應力狀態假設。

基于直法線不變假設，層合板的變形分析可簡化為對中面的變性分析。由于層合版沿厚度方向上具有非均質性，在鋪層間應力不一定連續，但在每一單層中，沿厚度方向的應力變化是連續函數，故可近似為先分層積分再求和的形式：

(14)

(15)

式中 {N}為層合板所受合力；{M}為層合板所受合力矩；zk為各層坐標。

層合板的合力及合力矩可用矩陣表示：

(16)

式中ε0為層合板的中面應變矩陣；k為曲率矩陣；A為拉伸剛度矩陣；B為耦合剛度矩陣；D為彎曲剛度矩陣。

式(16)即為用應變表示內力的一般層合板的物理方程。對層合板的物理方程進行矩陣運算即可得到層合板的應變矩陣。

2 數值仿真

某型固體火箭整流罩結構外型面為哈克曲線，基本壁厚5 mm，曲線方程為

纏繞纖維的材料參數由1.1節中方法得到，如表1所示。

表1 碳纖維的材料參數

模型中設定單層纖維的厚度為0.25 mm，纖維鋪層的方向與層數為[0/90/45/-45/0]4，總厚度為5 mm，模型的鋪層設計如圖3所示。

有限元的網格劃分情況如圖4所示。

在殼體尾端截面施加固支邊界條件，其模態計算結果如表2與圖5所示。為便于對比分析，特將正交方向的2個模態合并。

鑒于結構低頻振動特性對于整流罩殼體性能的影響更為顯著，對GJB 150.16A-2009《軍用裝備實驗室環境試驗方法 第16部分 振動試驗》中給出的隨機振動條件進行裁剪，隨機振動計算輸入條件如圖6所示。

圖3 模型的鋪層設計

圖4 模型的網格劃分

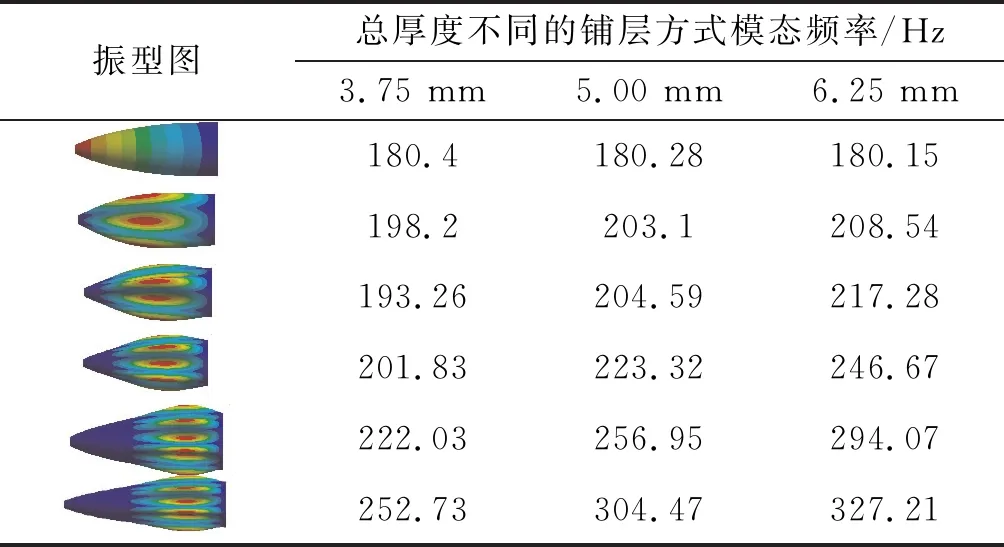
表2 總厚度不同的鋪層方式的模態頻率

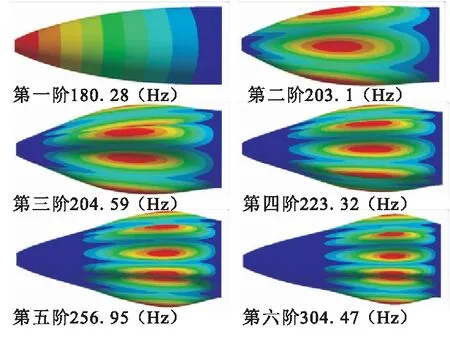
圖5 整流罩模型前六階模態圖

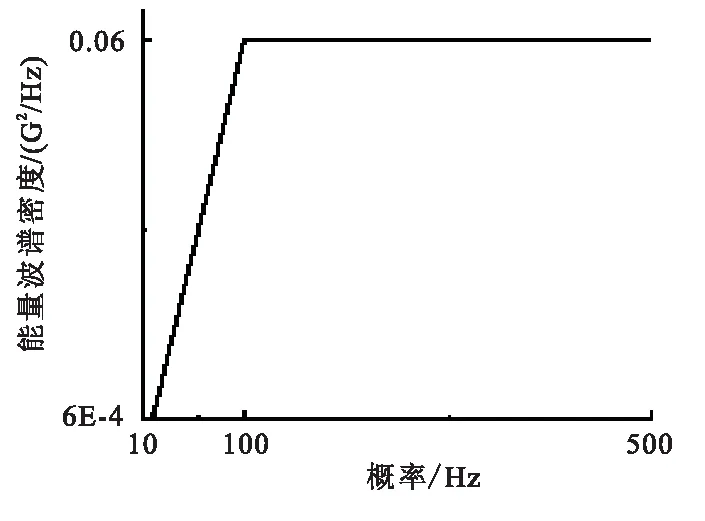
圖6 隨機振動輸入的功率譜密度

整流罩殼體的最大應力云圖、最大應變云圖和位移響應云圖如圖7所示。可見，在給定的邊界條件和輸入條件作用下，整流罩殼體頭部的振動位移最大，尾端應力最大，而最大應變則處在整流罩殼體的中后部。

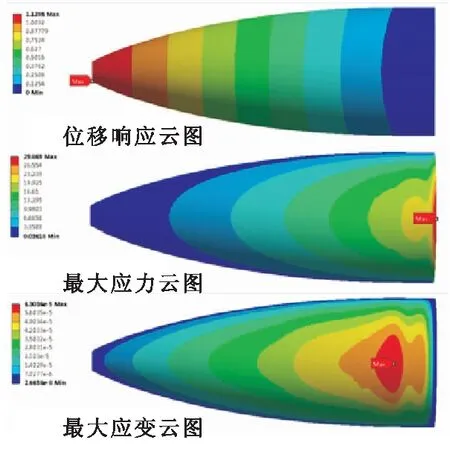
圖7 隨機振動結果云圖

3 規律分析

3.1 殼體厚度的影響

重量指標是固體火箭整流罩的關鍵參數，仿真過程中通過改變層的方式[0/90/45/-45/0]3(總厚3.75 mm)、[0/90/45/-45/0]4(總厚5.00 mm)、[0/90/45/-45/0]5(總厚6.25 mm)，以改變整流罩殼體基本壁厚，模態仿真結果見圖8。

由圖8可看出，隨著殼體厚度增加，在分析頻段內，除一階彎曲振動模態頻率未發生顯著改變外，整流罩殼體呼吸模態頻率均得到明顯提升。進一步提取總厚度不同的算例其各相同振型下的模態頻率，如表2所示。能明顯發現，隨著模態階數的升高，在同一振型情況下，厚度對材料結構的性能影響愈來愈大。

在第2節所示橫向隨機振動輸入條件下3個算例的最大位移功率譜密度曲線對比，如圖9所示。

可發現，在給定的振動輸入條件下，不同厚度算例對應的整流罩殼體振動位移曲線基本一致。這是由于對于給定的振動輸入條件，殼體一階彎曲振動模態的影響最為顯著，而殼體厚度的增加對于一彎模態的影響較小，導致位移功率譜密度曲線未呈現明顯差異。實際結構中，整流罩與下面級發動機的連接方式通常為多點連接，在這中連接形式下，整流罩殼體的呼吸模態對于其振動特性的影響將不容忽視。

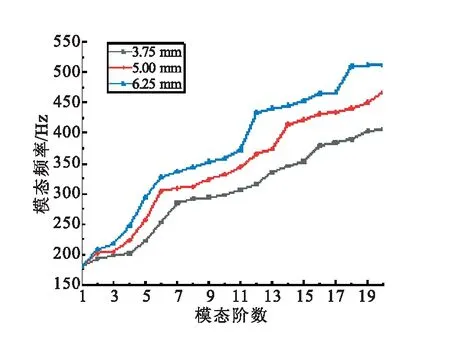
圖8 總厚度不同算例的模態頻率對比

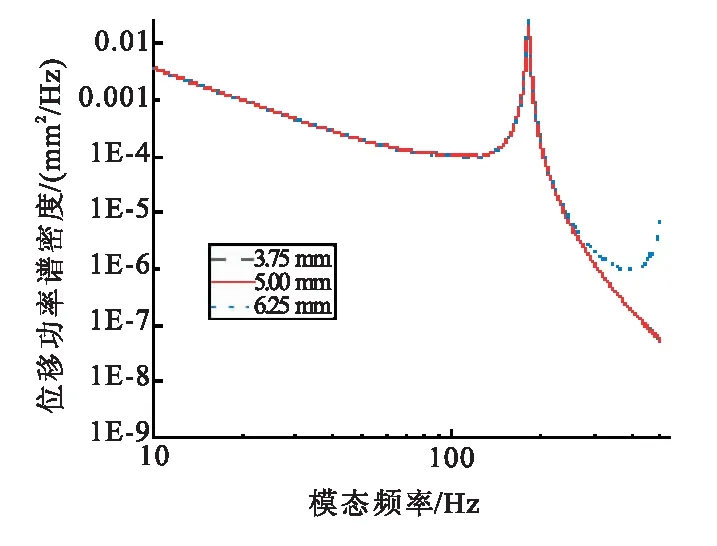
圖9 總厚度不同算例的位移功率譜密度對比

圖10給出了整流罩殼體底部8點固支邊界條件下的隨機振動仿真結果。結果表明，隨著殼體厚度的增加，殼體的低頻振動響應曲線整體向高頻偏移，厚度增加33%，模態向高頻偏移4%。

3.2 鋪層方式的影響

在整流罩厚度5 mm以及單層厚度0.25 mm保持不變的情況下，選擇圖11中的4種鋪層方式算例，分別進行仿真模態計算。

根據計算結果可看出，在[0/90/45/-45/0]4鋪層方式下，即當0°、45°和90°鋪層同時存在的情況下，其模態頻率相對較高。不同鋪層方式對應的結構振動響應曲線見圖12。

由圖12可以看出，采用[0/90/45/-45/0]4鋪層方式時，受到整流罩殼體模態頻率的提高，結構的低頻振動水平顯著降低。在保證整流罩殼體厚度不變的情況下，通過優化鋪層方式，能夠顯著改善結構的低頻振動特性。

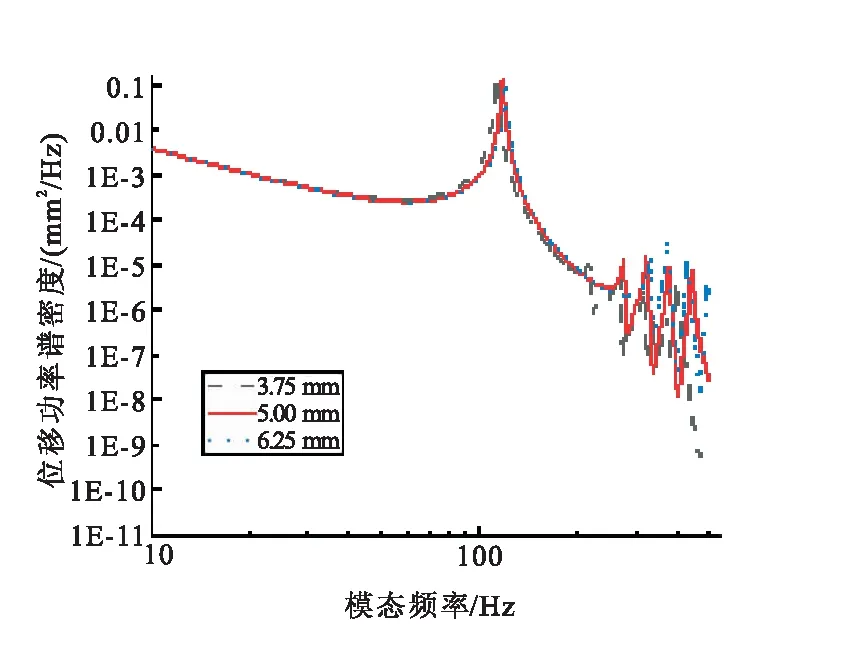
圖10 底部8點固支邊界條件下的隨機振動仿真結果

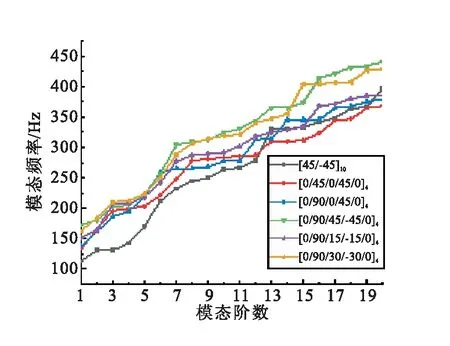
圖11 不同鋪層方式算例的模態頻率對比

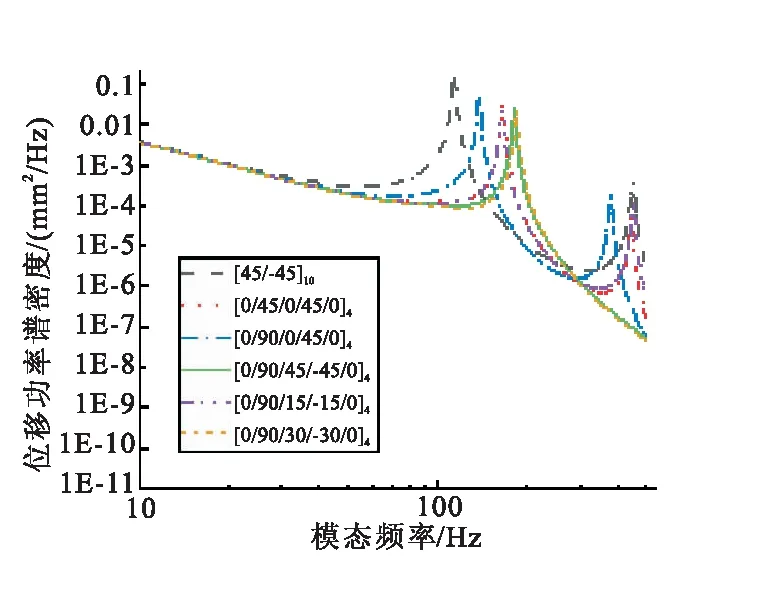
圖12 不同鋪層方式算例的隨機振動響應對比

4 結論

(1)殼體厚度對整流罩殼體呼吸模態的影響較大，在工程中常用的隨機振動輸入條件作用下，厚度變化對結構振動響應的影響較小。

(2)鋪層方式對整流罩殼體的振動特性影響顯著，通過優化鋪層方式來提高整流罩殼體剛性是更為有效的措施。