基于協方差矩陣稀疏表示的寬帶相干信號測向方法

王 凱，張海勃，宋 起，劉 勇

(西安測繪總站，陜西 西安 710054)

0 引 言

寬帶信號在各種雷達和通信系統中得到了越來越廣泛的應用，因此對寬帶信號的測向也逐漸成為陣列信號處理領域的一個研究熱點。在實際應用中，由于受到多徑等因素的影響，陣列接收機可能面臨著多個相干信號混疊的環境，這給常規陣列測向方法帶來了極大的挑戰。

非相干類寬帶信號測向方法將寬帶信號分解為多個窄帶分量之后，對每個窄帶分量依據窄帶子空間方法進行獨立處理，該方法在每個頻率點處都面臨著觀測協方差矩陣缺秩的問題，難以有效分辨多個相干寬帶信號[1]。相干寬帶信號測向方法首先對信號帶寬內各頻率分量進行聚焦，得到特定參考頻率點處的窄帶觀測協方差矩陣，此類方法中的聚焦過程能夠較好地消除信號之間相關性的影響，即使在多個入射信號完全相干的情況下，也能夠將它們分辨開來[2-3]。然而，仿真結果表明，相干子空間類寬帶測向方法的性能也會隨著入射信號之間相關性的增強而顯著下降。同時，非相干子空間類和相關子空間類測向方法都需要利用入射信號個數的先驗信息。在各種非合作偵察系統中，對寬帶信號特別是相干寬帶信號的源個數進行估計也是一個難點問題。

近年來稀疏重構技術在信號處理領域得到了廣泛的關注和應用，在陣列信號處理領域也取得了部分研究成果，如GMF方法[4-5]、FOCUSS方法[6]、L1-SVD方法[7]和JLZA-DOA方法[8]等。L1-SVD方法和JLZA-DOA方法已經被推廣應用于解決對寬帶信號的測向問題[7-8]，它們對入射信號個數先驗信息的依賴性較弱，且能夠較好地適應相干寬帶信號。然而，寬帶L1-SVD方法和JLZA-DOA方法都需要將寬帶信號分解為窄帶分量，并在各離散頻率點上獨立地得到1組測向結果。一般情況下，在各個頻率點處所得到的測向結果往往有較大的差異，因此L1-SVD方法和JLZA-DOA方法可能會面臨各離散頻率點處測向結果的融合問題。本文直接從寬帶信號陣列觀測數據的協方差矩陣出發，首先將協方差矩陣中部分元素重排得到一個新的觀測向量，該向量可表示為各入射信號分量的線性疊加，因此可借助稀疏表示技術分離這些信號成分，并同步實現對寬帶入射信號的波達方向估計。新方法很好地避免了頻域分解和聚焦等過程，因此不需要對入射信號進行角度預估，且不會受到信號之間相關性的影響。此外，新方法也不需要入射信號個數的先驗信息，因而能夠較好地適應電子偵察等非合作測向環境。

1 問題描述

假設K個相干寬帶信號從θ=[θ1,…,θK]方向同時入射到M元線性陣列上，t時刻的陣列輸出為：

(1)

(2)

可見Rp,q中含有K2個信號分量，當p=q時還含有未知的噪聲功率成分，直接通過對R進行分析并提取其中的信號分量以估計其入射方向較為困難。因此現有方法都是利用頻域分解的方式將寬帶接收模型轉化為窄帶模型[1-3]，本文采取的方法是直接對觀測協方差矩陣的成分進行分析以實現對寬帶相干信號的波達方向估計。

2 測向方法

為了簡化Rp,q的結構，本文只提取觀測協方差矩陣的第1列元素，并忽略受未知噪聲功率污染的第1個元素，得到各元素表達式如下：

p=2,…,M

(3)

對上述M-1個元素進行排列得到1個(M-1)×1維的觀測向量：

(4)

其中：

ak=[r(τk,2),…,r(τk,M)]T

(5)

(6)

其中ak由第k個信號在接收陣列上的傳播時延決定，這里將其定義為寬帶信號的陣列響應函數(或陣列流形)。在假設接收陣列滿足無模糊測向約束的條件下，ak由該信號的入射方向唯一確定，因此也可將ak寫成θk的函數形式a(θk)。下文將在不引起混淆的情況下，對ak和a(θk)2種形式交替使用。式(4)表明觀測向量y可表示為K個入射信號所對應陣列流形的加權和，如果能夠從y中分離各信號分量γkak，則利用從ak到θk的逆映射就能夠估計出K個信號的入射方向。

本文借助稀疏表示技術實現由y估計θ的過程。首先假設參考信號相關函數r(τ)先驗已知(仿真實驗部分將給出一種由觀測數據估計r(τ)的方法)，則對從θ方向入射的信號，其對應的陣列響應函數a(θ)可直接通過對r(τ)進行抽樣得到。依據實際測向精度需求，對信號可能的入射空域進行離散采樣，得到角度集Θ，在該角度集上依據式(5)中的陣列流形構造冗余字典集AΘ，則觀測向量y在該字典集AΘ上具有稀疏表示形式：

y=AΘγ

(7)

式中：γ為AΘ的系數矢量，僅在K個信號的入射方向對應坐標處取非零值γk(k=1,…,K)，因而滿足稀疏特性。

在式(7)線性約束下，通過求解如下稀疏表示問題可恢復其中的K個信號分量，即：

min‖γ‖0,subject toy=AΘγ

(8)

式中：e0范數‖γ‖0表示γ中非零元素個數。

(9)

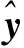
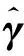
3 觀測向量擾動分析

假設陣列接收機共采集到N組觀測樣本x(1),…,x(N)，則觀測向量y中第p個元素的估計值為：

(10)

(11)

(12)

(13)

(14)

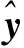
(15)

(16)

(17)

(18)

式(17)可簡化為：

(19)

因此：

(20)

(21)

(22)

因此，對象函數(9)中的擬合誤差門限一種直觀取值為：

(23)

式中：μ為擬合誤差門限調整因子，其經驗取值為0.5～2。

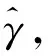
4 仿真實驗

假設2個相對帶寬為20%的等功率相干寬帶信號從10°和18°方向同時入射到12元均勻線陣上，陣列相鄰陣元間距等于入射信號中心頻率對應波長的一半，采樣頻率等于入射信號最高頻率的2倍。新方法在構造冗余字典集型A(Θ)的過程中，將[-90° 90°]空域按1°角度間隔進行劃分，并借助Matlab軟件中periodogram函數由觀測數據估計觀測數據功率譜P(ω)，然后依據陣列結構和各離散方向計算出字典集內各元素對應的傳播時延后，由IFFT變換估計字典集中各元素[10]。為減小計算量，本文在估計自相關函數時只利用了第1個通道的數據。新方法中擬合誤差門限調整因子μ取為1。仿真過程中選取雙邊相關變換(TCT)方法[3]作為性能比較對象，并依據測向方法對2個入射信號的分辨概率評價算法性能，當2個最顯著的空間譜峰位于信號真實入射方向附近，且測向偏差均不大于3°時，認為正確分辨。

首先固定采樣點數為512，2個信號的信噪比從-5 dB到10 dB變化，在每個信噪比取值下進行1 000次蒙特卡羅仿真，得到新方法和TCT方法對2個信號的分辨概率如圖1所示。隨后，固定2個信號的信噪比為-3 dB，快拍數從32到4 096變化，在每個快拍數取值下進行1 000次仿真實驗，得到新方法和TCT方法對2個信號的分辨概率如圖2所示。

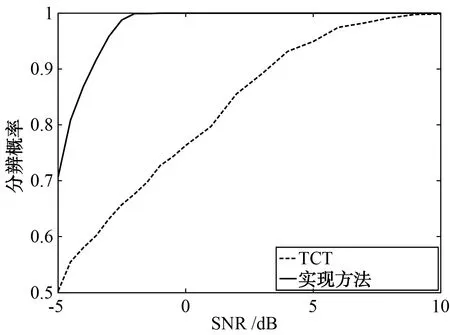
圖1 分辨概率隨信噪比變化情況

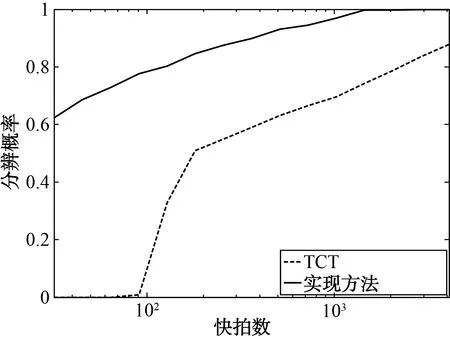
圖2 分辨概率隨快拍數變化情況

從圖1和圖2的仿真結果可以看出，新方法對寬帶相干信號的測向性能顯著優于TCT方法，且能夠更好地適應低信噪比和小樣本數的實際環境。

5 結束語

本文針對寬帶相干信號的測向問題，提出了一種基于協方差矩陣稀疏表示的測向方法。新方法不需要進行頻域分解和聚焦等處理，且不需要入射信號個數的先驗信息。仿真結果表明，新方法具有比已有相干寬帶測向方法更強的超分辨能力，且能夠更好地適應低信噪比和小樣本等實際應用環境。