關于高三數(shù)學復習課變式教學的實踐

談曉輝

高中數(shù)學課堂活動中，變式教學是重要的教學方式，也是一種使用比較成熟的方式。在高三數(shù)學復習課中，解題量非常多，需要開展生動有趣的解題活動，引導學生體驗和感受數(shù)學的魅力和樂趣，使得學生保持積極的學習態(tài)度。借助變式教學，可以通過以點帶面的方式，加強學生指導和引導，減輕學生課堂學習負擔，取得非常好的教學效果。通過這樣的課堂教學活動，充分調(diào)動學生的積極性和主動性，提高學生復習效果。

一、不斷擴展和延伸，開展變式教學活動

高三數(shù)學復習教學中，為了幫助學生解決數(shù)學問題，需要對問題原有條件進行延伸和擴展，通過相應的對比分析，設計相應的變式問題，借助這樣的變式訓練活動，加深學生對數(shù)學知識的理解，有效利用數(shù)學知識解決問題，開闊學生的眼界和視野，切實做到舉一反三，實現(xiàn)復習教學目標。

例題：A是河流岸邊的一點，B是河對岸的一點，為了測量A、B兩點間的距離，需要在岸邊取出基線AC，測量得出AC的距離是120米，∠BAC=45°，∠BCA=75°，求A和B之間的距離。

分析：在解題的過程中，根據(jù)△ABC中的A、C兩個角，可求出B的度數(shù)，結(jié)合正弦定理，可求解出A、B之間的距離。此題解答的過程中，角B求解是關鍵，結(jié)合正弦定理公式，可以很快完成題目求解。

變式：河岸邊選擇兩點C和D，兩點之間的距離是40米，可以測量出∠BCA=60°，∠ACD=30°，∠CDB=45°，∠BDA=60°，求A、B兩點之間的距離。

通過這樣的變式訓練，為學生解題提供更為廣闊的背景，學生可以利用例題的解題方式，將正弦定理和余弦定理有效結(jié)合，完成題目的解答。在具體的解題過程中，根據(jù)題目已知內(nèi)容，結(jié)合△ADC和△BDC，利用正弦定理，求出AC和BC的值，之后在△ABC中，利用余弦定理求出A、B之間的距離。

因此，高三數(shù)學復習課堂教學中，需要結(jié)合習題內(nèi)容進行擴展和延伸，通過類比和分析，開展變式教學活動，引導學生有效利用數(shù)學知識，提高學生解題能力。

二、多個角度思考分析，有效開展變式教學

高三數(shù)學復習教學中，有效利用變式教學，引導學生靈活審視數(shù)學問題，從多個角度和層次學習和探究，在課堂活動中，需要引導學生利用發(fā)散思維探究數(shù)學問題，完成問題的變式訓練。在實際的課堂活動中，將問題組呈現(xiàn)給學生，為學生提供變式訓練的平臺和機會，鍛煉學生數(shù)學思維，更加靈活地解決數(shù)學問題，提高復習課堂教學效果。

例題：某商店按照出廠價每瓶3元批發(fā)一種飲料，通過對以往的數(shù)據(jù)進行統(tǒng)計分析發(fā)現(xiàn)，如果售價為每瓶4元，每個月可以銷售400瓶，如果每瓶售價降低0.5元，可以多銷售40瓶。如果每個月的進貨量完全售完，設計相應的方案，售價定為多少，購買多少瓶飲料，可以獲取最大利潤？

變式1：拋物線f（x）=-x?+ax（a∈R）和x軸圍成的圖形內(nèi)接矩形，矩形一邊在x軸上，求解周長最大時矩形兩邊的比。

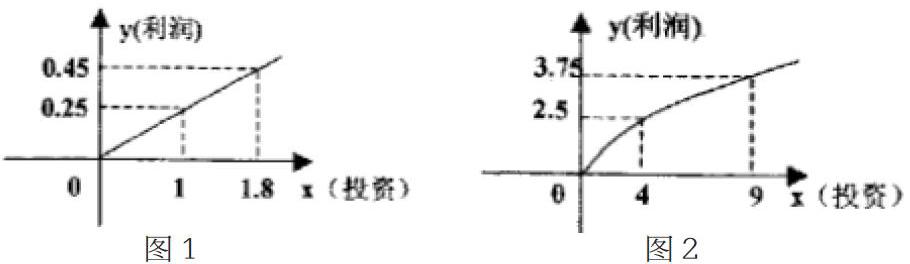
變式2：某個企業(yè)生產(chǎn)A、B兩種產(chǎn)品，A產(chǎn)品的利潤和投資成正比，關系如圖1所示，B產(chǎn)品的利潤和投資的平方根成正比，關系如圖2所示。（1）求A、B兩種產(chǎn)品利潤和投資的函數(shù)關系式。（2）如果企業(yè)將10萬元投入到A、B產(chǎn)品的生產(chǎn)中，應當如何分配，才能夠使得企業(yè)獲得最大利潤？最大利潤是多少？

通過這樣的方式設計問題，通過問題的解答完成信息內(nèi)容傳遞，針對性地培養(yǎng)學生綜合能力，通過變式訓練，突破學生思維定勢，從主題到變式，結(jié)合問題設計的關鍵點，完成題目求解，鍛煉學生數(shù)學思維能力。

三、深入發(fā)掘問題本質(zhì)，開展變式教學活動

高三數(shù)學復習課程中，通常會以特殊問題作為基礎，對其條件、結(jié)論開展分析和對比活動，探究數(shù)學問題結(jié)構(gòu)，開展相應的歸納和總結(jié)，構(gòu)建相應的數(shù)學模型，實現(xiàn)問題思路由特殊到一般的轉(zhuǎn)變。問題的形式非常多，準確把握本質(zhì)可以保證變式教學的有效開展，促使學生更加全面地了解數(shù)學問題，準確把握問題本質(zhì)，提高復習活動的有效性。

例題：等差數(shù)列{an}中，a1=31，公差d=-8。（1）求數(shù)列{an}的通項公式。（2）求數(shù)列{an}前n項和的最大值。

變式1：{an}是等差數(shù)列，每一項都不為零，a1>0，公差d<0，若S10=0，求解{an}前n項和的最大值。

變式2：{an}是等差數(shù)列，a1=25，S17=S9，求Sn的最大值。

在等差數(shù)列前n項和和最值問題的解決中，可以利用函數(shù)求解最值，根據(jù)通項公式進行求解，結(jié)合相應的性質(zhì)求解各項的值。在解題中，需要結(jié)合母題求解，根據(jù)已知條件和等差數(shù)列性質(zhì)和公式。開展變式練習，對其進行對比和分析，總結(jié)解題思路和技巧，引導學生推理和歸納，完成題目的有效解答，提高復習課堂效果。

四、加強思維能力培養(yǎng)，優(yōu)化變式教學活動

高三數(shù)學復習課程中，解題能力主要在問題發(fā)現(xiàn)、分析和解決等過程中體現(xiàn)，注重學生數(shù)學能力培養(yǎng)，有利于學生良好思維方式的形成。思維能力培養(yǎng)是課堂教學的重要任務，借助變式教學巧妙設計問題，實現(xiàn)學生思維能力培養(yǎng)。

例題：某人鑰匙鏈上有五把鑰匙，其中一把是家門鑰匙，忘記是哪一把，只能通過逐個嘗試的方式開門，恰好第三次打開門的概率是多少？

變式1：恰好第一次打開家門和恰好第三次打開家門的概率是否相同？說出原因。

變式2：如果此人有m把鑰匙，不重復地嘗試開門，第k次打開門的概率是多少？

變式3：如果此人有m把鑰匙，重復嘗試的情況下，第k次恰好打開門的概率是多少？

借助這樣的方式，引導學生思考隨機事件概率問題，開展課堂思考和反思活動，鍛煉學生數(shù)學思維能力。

高三數(shù)學復習課中，有效利用變式教學，展示數(shù)學問題的演變和形成，從中探究相應的數(shù)學規(guī)律，總結(jié)數(shù)學問題解決方式，深層次理解和探究數(shù)學問題，提高學生數(shù)學思維能力，提高課堂教學效率和質(zhì)量。