具正負(fù)系數(shù)和多變時(shí)滯的高階微分方程的振動(dòng)性

覃桂茳，劉玉周，楊甲山

（1.梧州學(xué)院大數(shù)據(jù)與軟件工程學(xué)院，廣西梧州543002； 2.梧州學(xué)院廣西高校行業(yè)軟件技術(shù)重點(diǎn)實(shí)驗(yàn)室，廣西梧州543002； 3.梧州學(xué)院機(jī)械與材料工程學(xué)院，廣西 梧州543002； 4.梧州學(xué)院廣西高校圖像處理與智能信息系統(tǒng)重點(diǎn)實(shí)驗(yàn)室，廣西梧州543002）

0 引 言

在微分方程理論中，振動(dòng)性是其重要的分支之一，并廣泛應(yīng)用于物理力學(xué)、控制系統(tǒng)、時(shí)間延遲系統(tǒng)、電力系統(tǒng)、時(shí)變非線性反饋系統(tǒng)等。微分方程的振動(dòng)性廣受關(guān)注且成果頗豐[1-14]。但具有正負(fù)系數(shù)和多變時(shí)滯的高階方程振動(dòng)性的研究成果卻很少。考慮以下微分方程

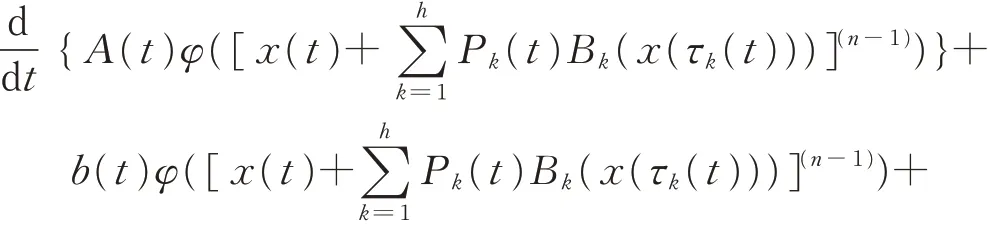
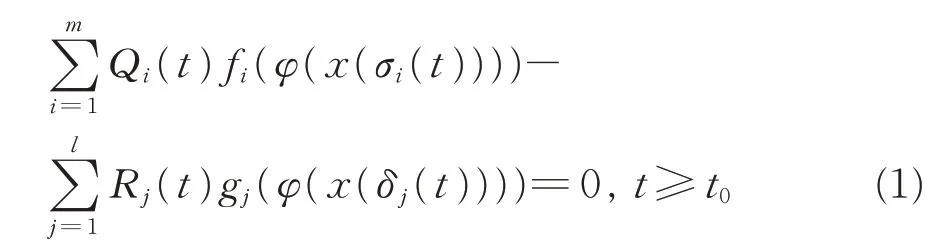
的 振 動(dòng) 性，其 中n ≥2 為 偶 數(shù)，t0≥0 為 實(shí) 常 數(shù)；φ(u)=|u|γ-1u,γ ＞0 為實(shí)常數(shù)；h ≥1，m ≥1，l ≥1，均為整數(shù)。全文總假設(shè)條件(H0)～(H5)成立：

(H0) 函 數(shù) A(t)， Pk(t)， b(t)， Qi(t)，Rj(t)∈C([t0,+∞),[0,+∞)),k=1,2,…,h；i=1,2,…,m； j=1,2,…,l( 下 同 , 略)； Bk(u)，fi(u),gj(u)∈C(R,R) 且 uBk(u)＞0(u ≠0)，ufi(u)＞0(u ≠0)，ugj(u)＞0(u ≠0)。

(H1) 函 數(shù) τk(t)∈C([t0,+∞),(0,+∞))，

(H2) 函數(shù)σi(t)=δj(t)=σ(t)∈C1([t0,+∞),

(H3) 存在常數(shù)0 ＜ηk≤1,αi＞0,βj＞0，使得當(dāng) u ≠0 時(shí) 有 Bk(u)/u ≤ηk， fi(u)/u ≥αi，并 且最終成立。

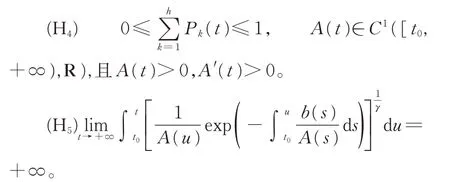
關(guān)于方程(1)的解及其振動(dòng)性的定義參見文獻(xiàn)[1-12]，本文只討論方程(1)的非平凡解。方程(1)包括了許多典型的微分方程，如二階Emden-Fowler型方程：

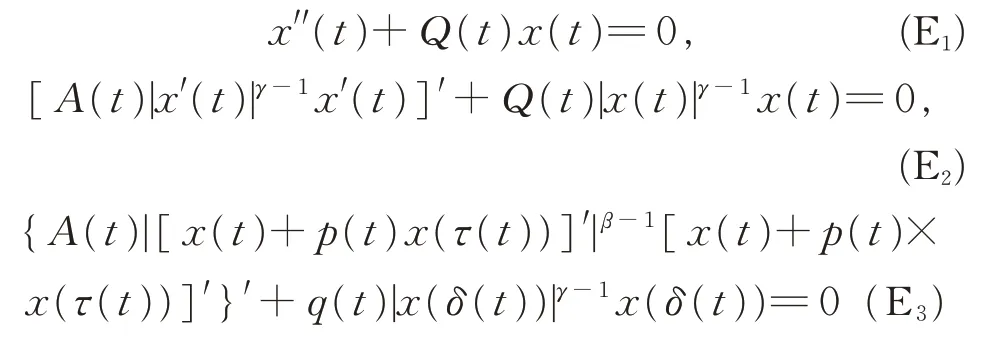
及具有正負(fù)系數(shù)的二階方程：

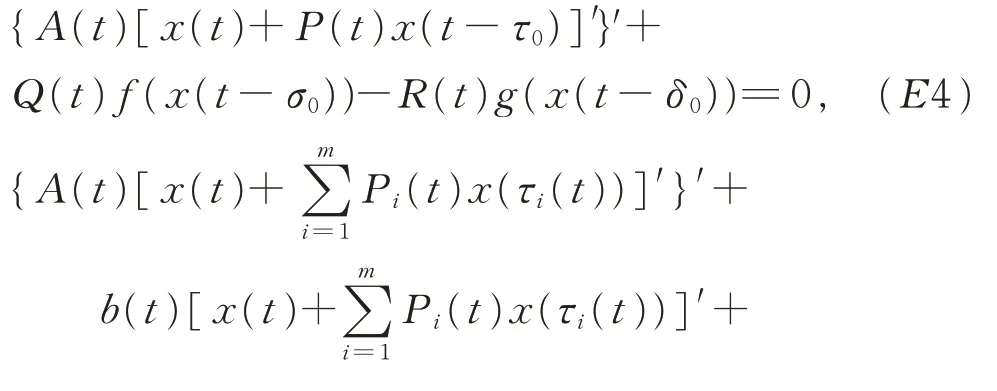
等。這些典型的微分方程已有許多很好的振動(dòng)準(zhǔn)則[1-12]。如KAMENEV[1]改 進(jìn) 了WINTNER 的 結(jié)果，得到了以下振動(dòng)準(zhǔn)則(稱之為Kamenev 型振動(dòng)準(zhǔn)則)：

定理A[1]若+∞（μ ＞1 為常數(shù)），則方程(E1)振動(dòng)。

之后，LI 等[2]將KAMENEV 的結(jié)果推廣到了二階半線性微分方程(E2)，得到

定理B[2]若如 存在常數(shù)k ＞γ，使得

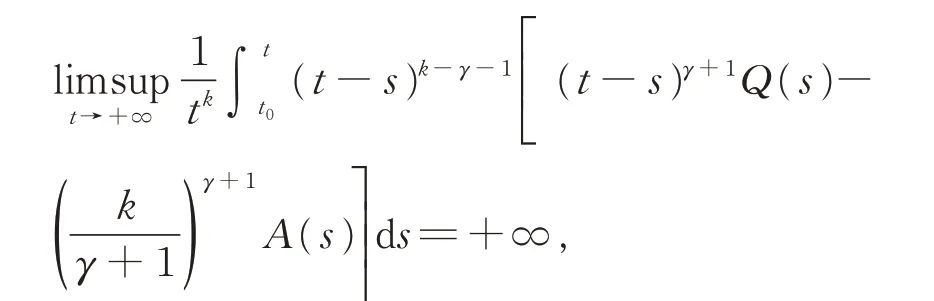
則方程(E2)振動(dòng)。

以此為基礎(chǔ),黃記洲等[3]研究了更一般的二階Emden-Fowler 型方程(E3)，并得到方程(E3)振動(dòng)的一系列新準(zhǔn)則，其Hille 型振動(dòng)準(zhǔn)則如下：

定 理C[3]設(shè)β ≥γ，A′(t)≥0，δ′(t)＞0，0 ≤p(t)＜1，且若 存 在 函 數(shù)φ ∈C1([t0,+∞),(0,+∞))，使得

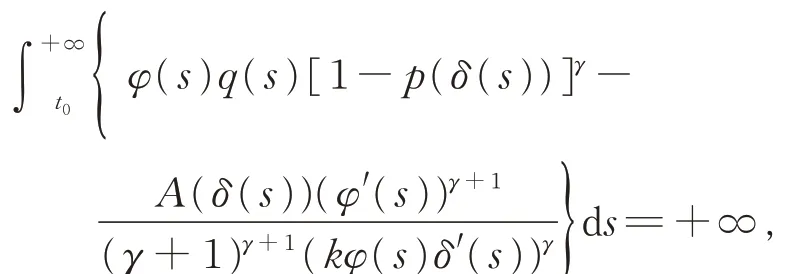
其中k ＞0 為常數(shù)，則方程(E3)振動(dòng)。

對(duì)具有正負(fù)系數(shù)的二階微分方程，仉志余等[4]率先研究了方程(E4)的振動(dòng)性，結(jié)果如下：

定理D[4]設(shè)0 ≤P(t)＜1，Q(t)≥0 且R(t)最終為負(fù)，若

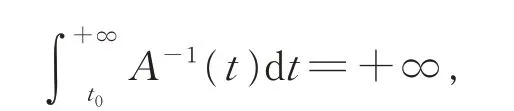
緊接著，楊甲山等[5]研究了一類廣泛的具有正負(fù)系數(shù)的二階方程(E5)的振動(dòng)性，放寬了文獻(xiàn)[4]的條件，得到了方程(E5)的振動(dòng)準(zhǔn)則(包括Hille 型準(zhǔn)則和Kamenev 型準(zhǔn)則等)。其他結(jié)果可參見文獻(xiàn)[6-10]，而對(duì)具有正負(fù)系數(shù)及多時(shí)滯的高階微分方程的振動(dòng)性研究成果目前還很少。

本文的目的是研究具有正負(fù)系數(shù)和多變時(shí)滯的高階阻尼微分方程(1)的振動(dòng)性，進(jìn)一步改進(jìn)并拓展現(xiàn)有的研究成果，使得定理A～定理D 成為本文結(jié)果的特例，最后用一些具體實(shí)例說(shuō)明本文的主要結(jié)論。

1 引 理

引入記號(hào)

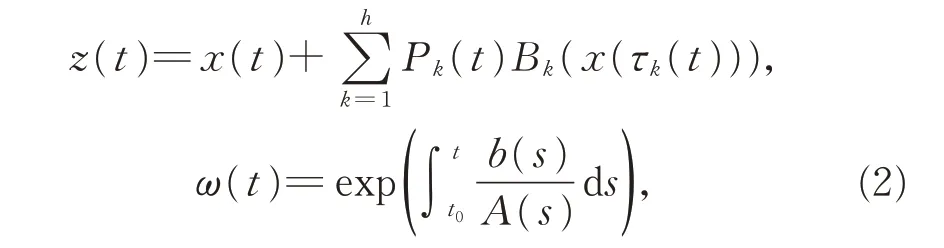
則方程(1)可寫為

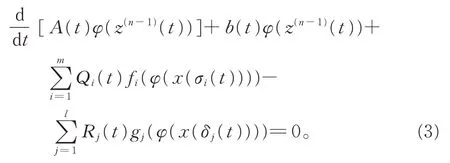
引理1[7]設(shè)u(t)在[t0,+∞)上是正的n 次可微函數(shù)，u(n)(t)最終定號(hào)，則存在t*≥t0和整數(shù)l(0 ≤l ≤n)，當(dāng)u(n)(t)≥0 時(shí)，n+l 為 偶 數(shù)；當(dāng)u(n)(t)≤0 時(shí)，n+l 為 奇 數(shù)，使 得 當(dāng)l ＞0 時(shí)，有u(k)(t)＞0，t ≥t*，k=0,1,…,l-1；且 當(dāng)l ≤n-1時(shí) ， 有 t ≥t*； (-1)l+ku(k)(t)＞0； k=l,l+1,…,n-1。

引理2[7]設(shè)u(t) 滿足引理1 的條件，且u(n-1)(t)u(n)(t)≤0(t ≥t*)，則對(duì)任意θ ∈(0,1)，存在常 數(shù)M ＞0，使 得 對(duì) 一 切 充 分 大 的t 有u′(θ t)≥Mtn-2u(n-1)(t)。

引理3[7]設(shè)a，b 為非負(fù)實(shí)數(shù)，則aλ-λabλ-1+(λ-1)bλ≥0，λ＞1，等號(hào)成立當(dāng)且僅當(dāng)a=b。

引理4設(shè)x(t)是方程(1)的最終正解，則

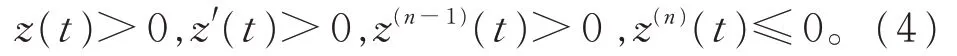
證明因?yàn)閤(t)是方程(1)的最終正解，不妨設(shè)當(dāng)t ≥T ≥t0時(shí)，x(t)＞0，x(τk(t))＞0，x(σi(t))=x(δj(t))=x(σ(t))＞0，于是

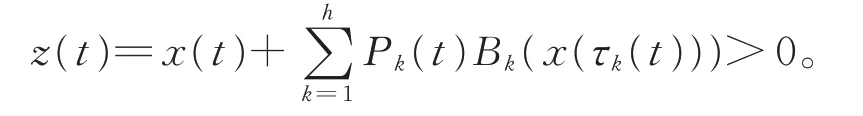
由方程(3)并注意到條件(H3)，得

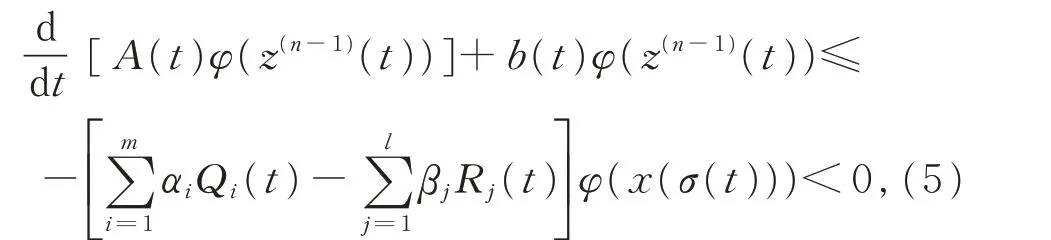
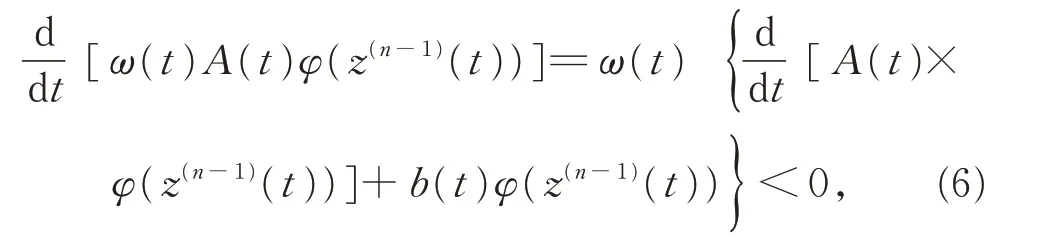
因此ω(t)A(t)φ(z(n-1)(t))是減函數(shù)，并且z(n-1)(t)最終定號(hào)，且能斷言：

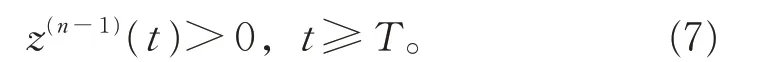
事實(shí)上，若z(n-1)(t)＜0，t ≥T。由式(6)，得

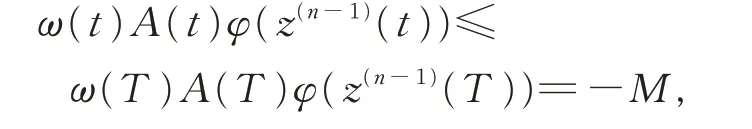
其中常數(shù)

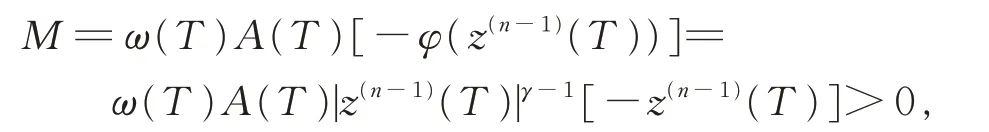
于是由上式得

進(jìn)一步，有

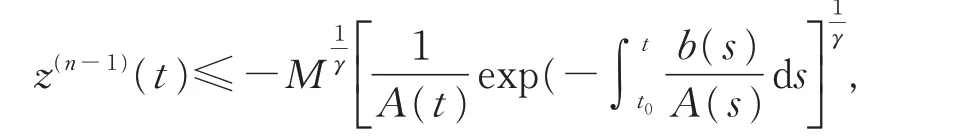
于是有

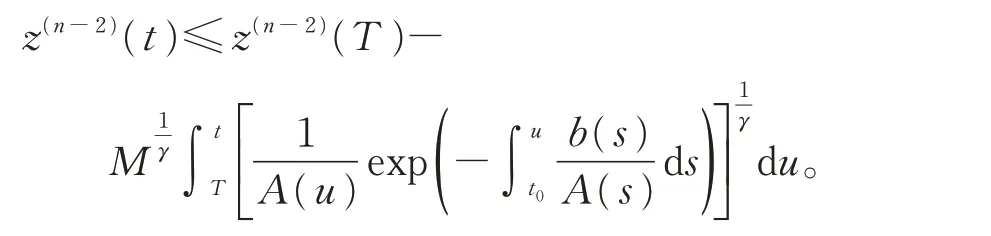
在 上 式 中 ，令 t →+∞，注 意 到 (H5)，得類 似 可 得這 與z(t)＞0 矛盾！故式(7)成立。

由式(5)知，

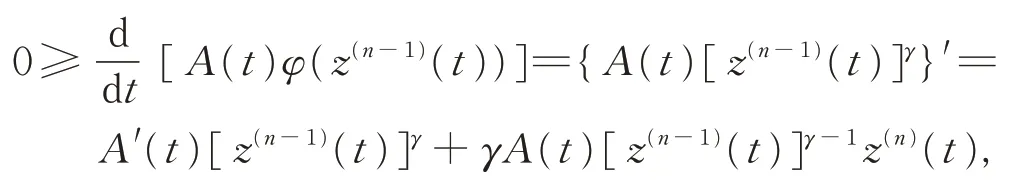
由此推得z(n)(t)≤0(t ≥T)。因?yàn)閚 是偶數(shù)，于是由引理1 中l(wèi) 為奇數(shù)，有z′(t)＞0(t ≥T)。 證畢。

2 方程（1）的振動(dòng)準(zhǔn)則

定 理 1如 果 存 在 函 數(shù) ρ(t)∈C1([t0,+∞),(0,+∞))，使得

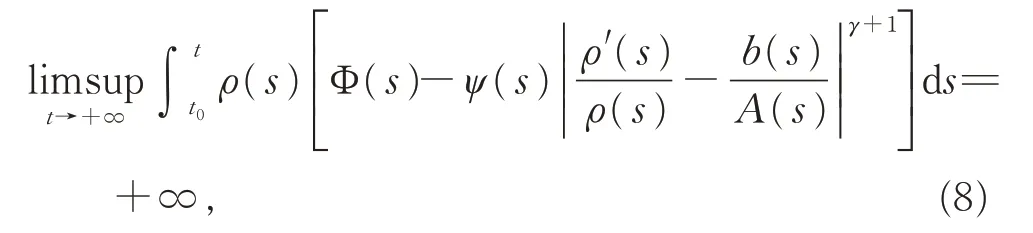
其中函數(shù)Φ(t)和ψ(t)的定義如下：

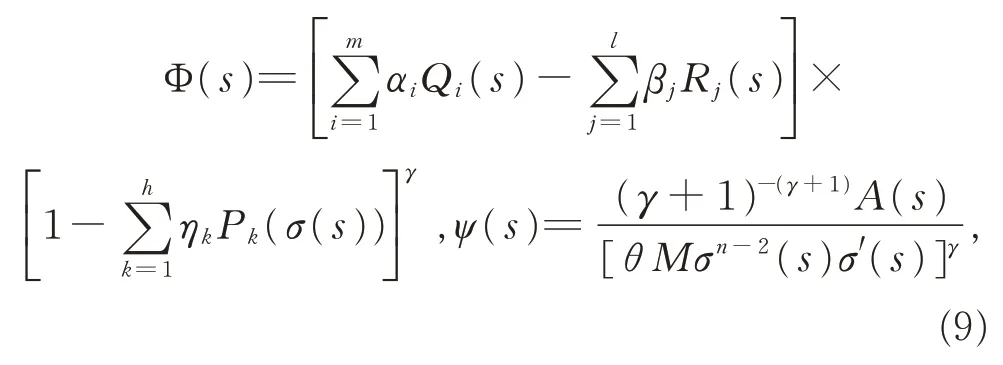
常數(shù)θ ∈(0,1)和M ＞0 同引理2，則方程(1)振動(dòng)。

證明設(shè)方程(1)存在非振動(dòng)解x(t)，不失一般性，設(shè)x(t)＞0,x(τk(t))＞0，x(σ(t))＞0，t ≥T ≥t0。由引理4 知，式(4)成立。于是由引理2，對(duì)任意0 ＜θ ＜1，存在常數(shù)M ＞0，有

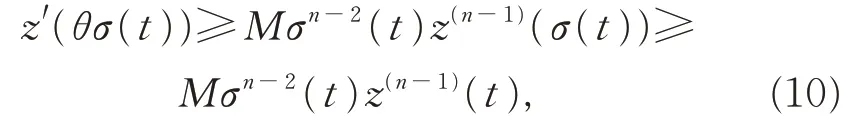
由式(2)的第1 個(gè)式子知，x(t)≤z(t)，于是

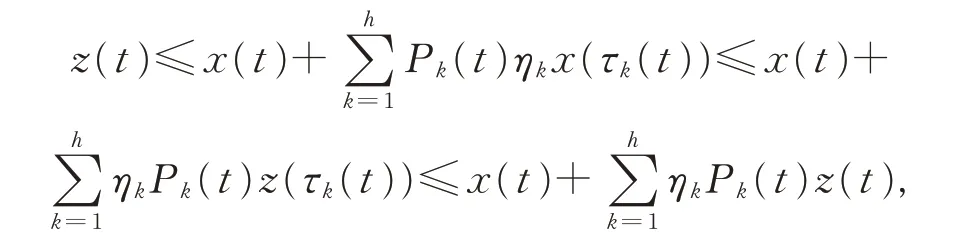
整理得

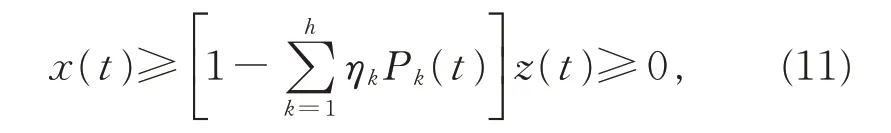
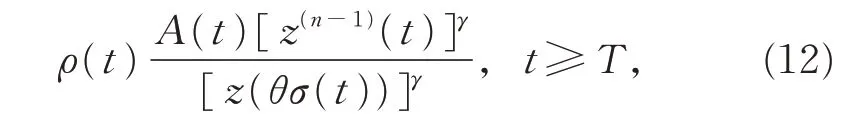
則V(t)＞0(t ≥T)，注意到式(5)、(10)和(11)，由式(12)可導(dǎo)出

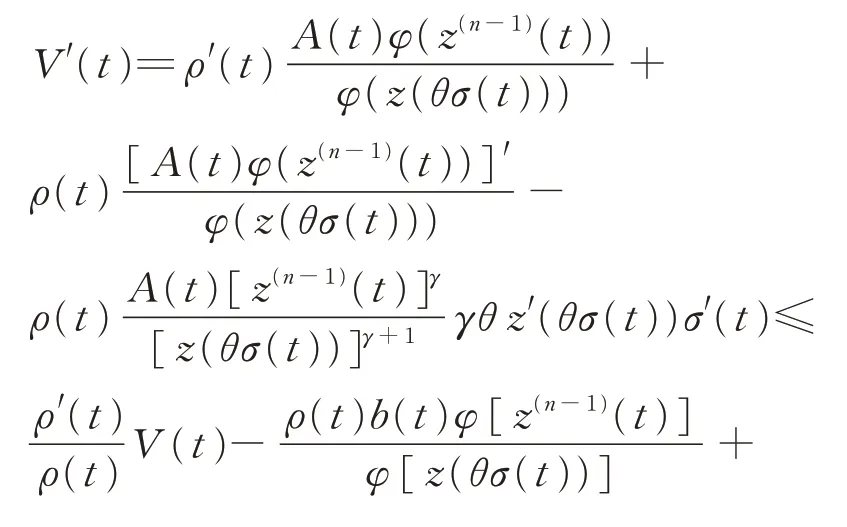
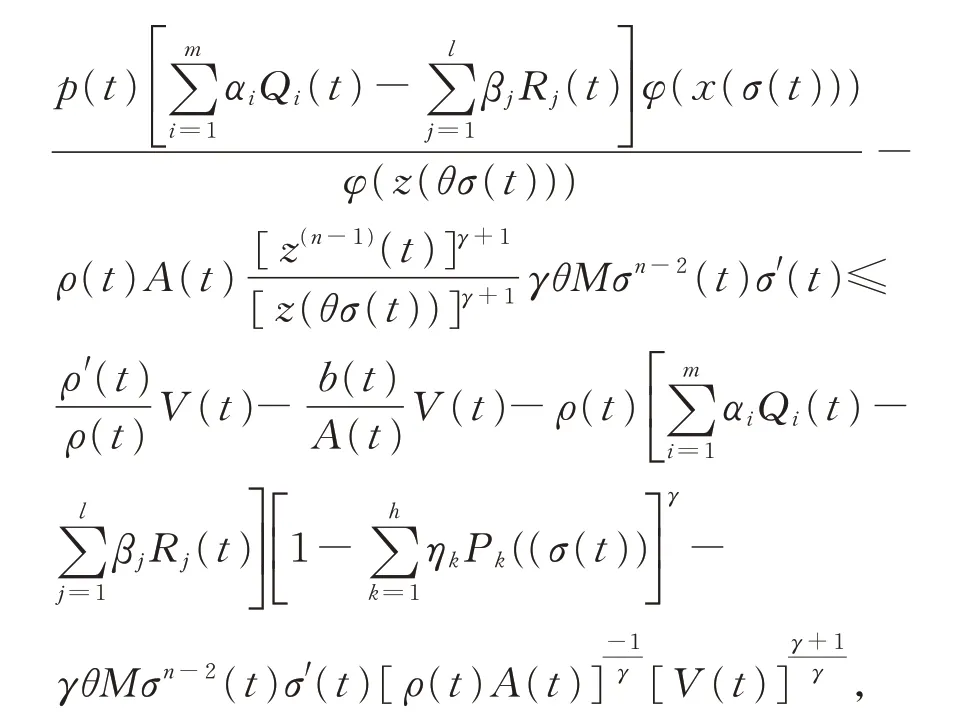
注意到式(9)的第1 個(gè)式子，當(dāng)t ≥T 時(shí)，由上式進(jìn)一步可得

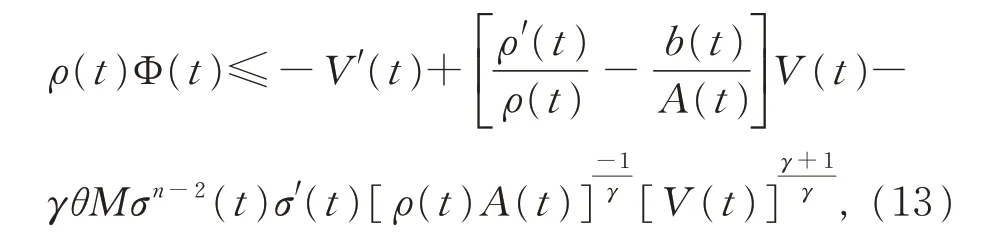
現(xiàn)取

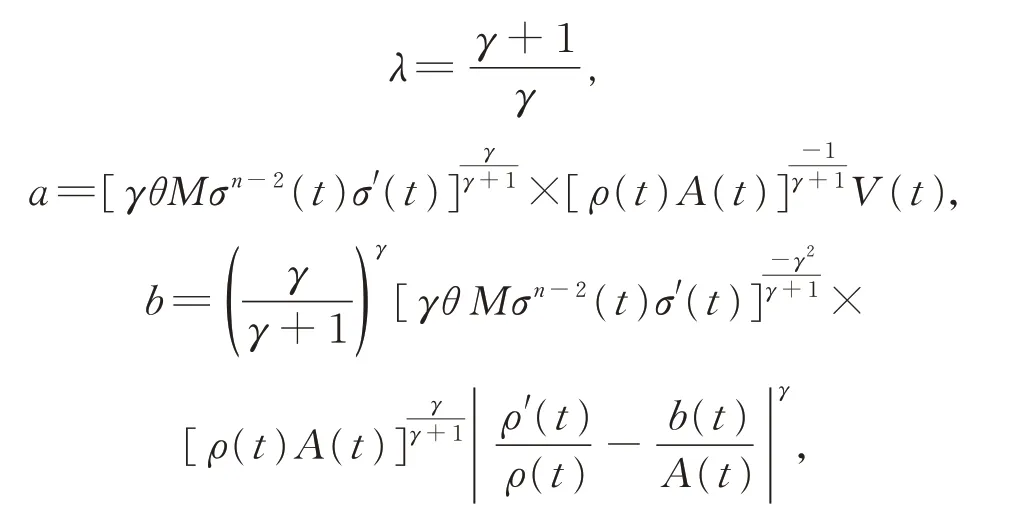
由引理3，有λabλ-1-aλ≤(λ-1)bλ，即

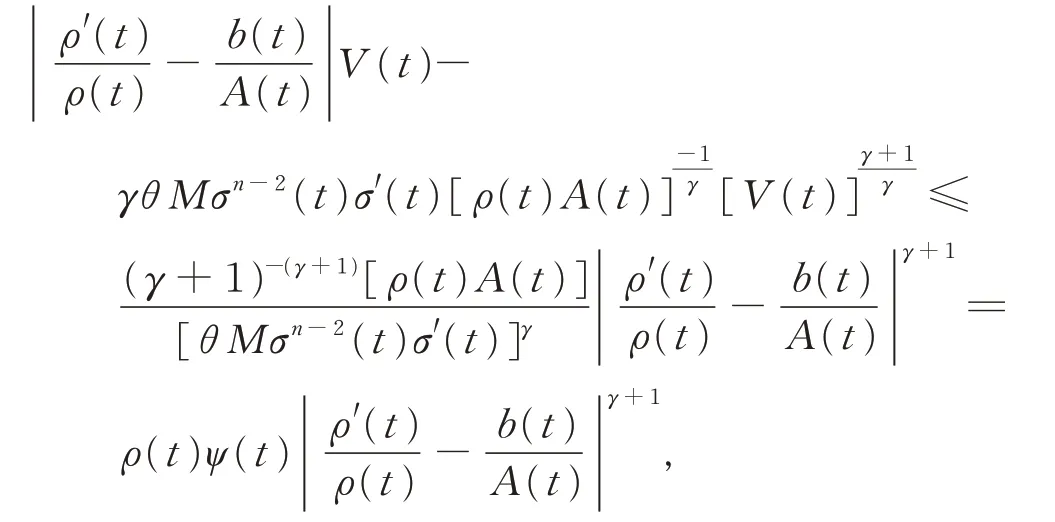
將上式代入式(13)，得

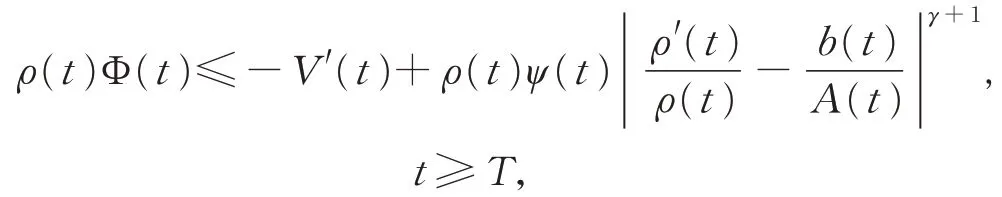
上式兩邊從T 到t 積分，可得

取上極限，則得到與式(8)矛盾的結(jié)果。定理1 證畢。

定 理 2如 果 存 在 函 數(shù) ρ(t)∈C1([t0,+∞),(0,+∞))及常數(shù)μ ＞γ，使得

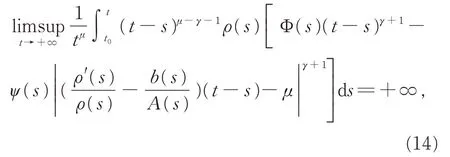
其中常數(shù)θ ∈(0,1)和M ＞0 的定義同引理2，而函數(shù)Φ(s)，ψ(s)的定義同式(9)，則方程(1)振動(dòng)。

證明若不然，則方程(1)存在非振動(dòng)解x(t)，不 失 一 般 性 ， 設(shè) x(t)＞0,x(τk(t))＞0，x(σ(t))＞0，t ≥T ≥t0。由 引 理4 知，式(4)成 立。定義函數(shù)V(t)如式(12)，則由定理1 的證明知，式(13)成立，即當(dāng)s ≥T 時(shí)，有

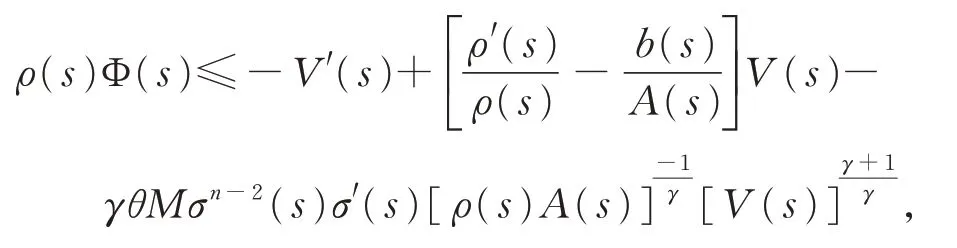
上式兩邊同乘以(t-s)μ，并從T 到t 積分，由分部積分法，整理得

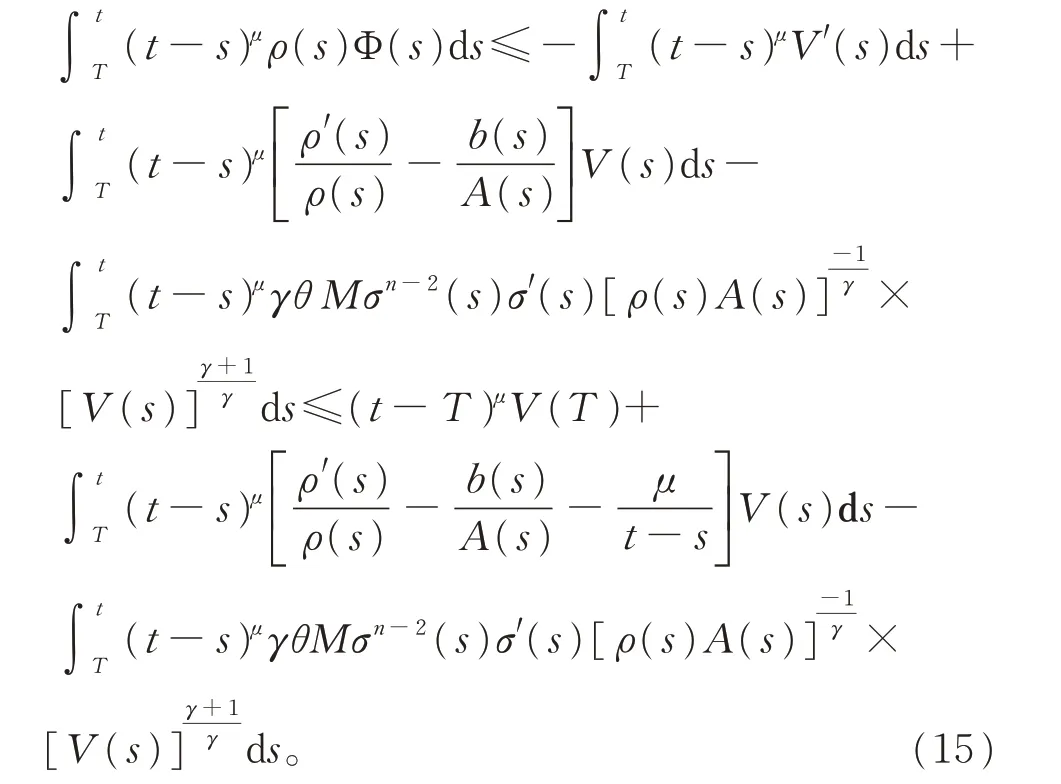
現(xiàn)取

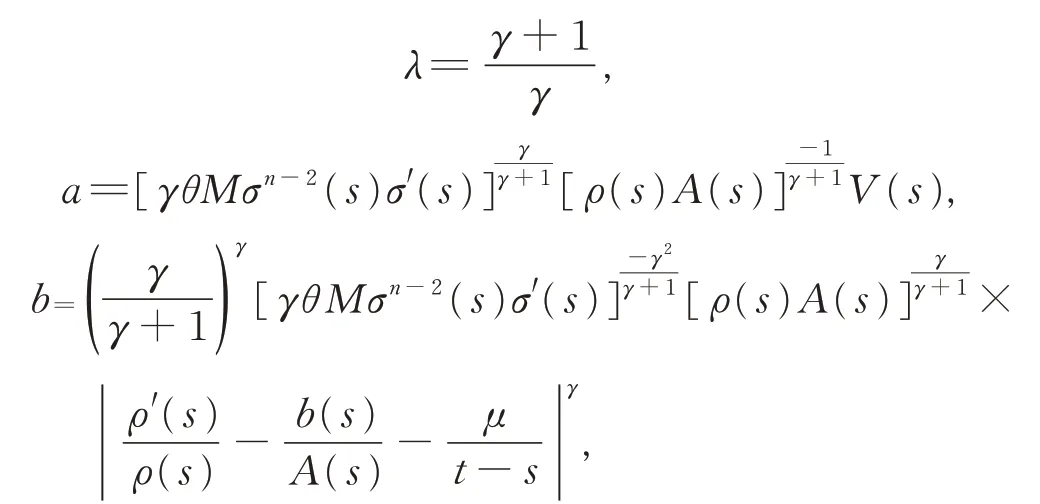
由引理3，有λabλ-1-aλ≤(λ-1)bλ，注意到式(9)的第2 個(gè)式子，可得

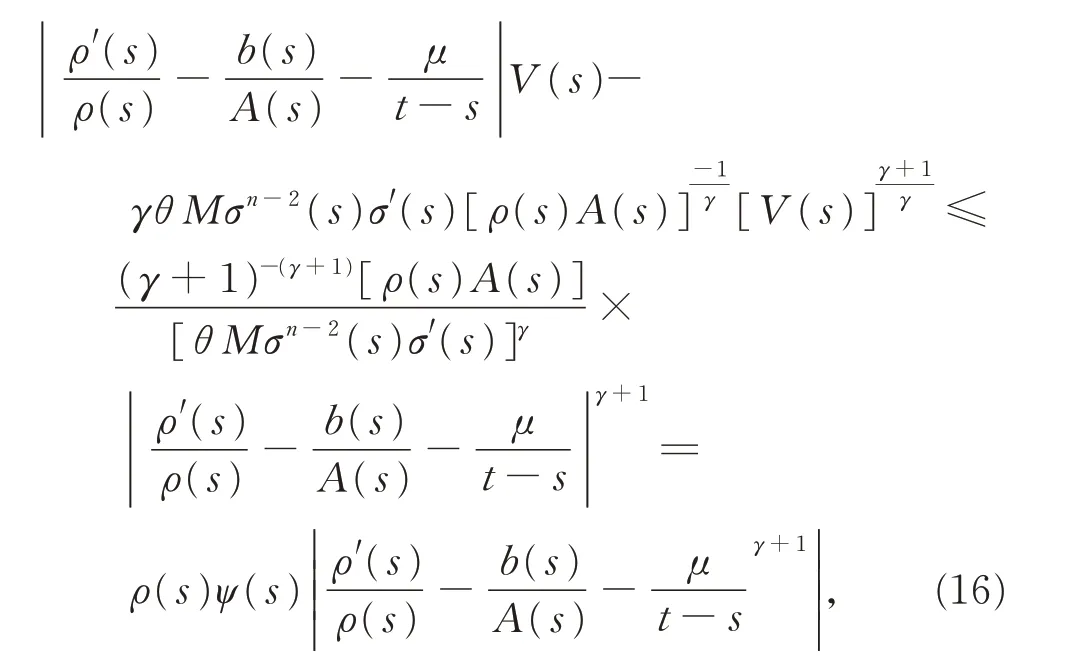
綜合式(15)、(16)，有

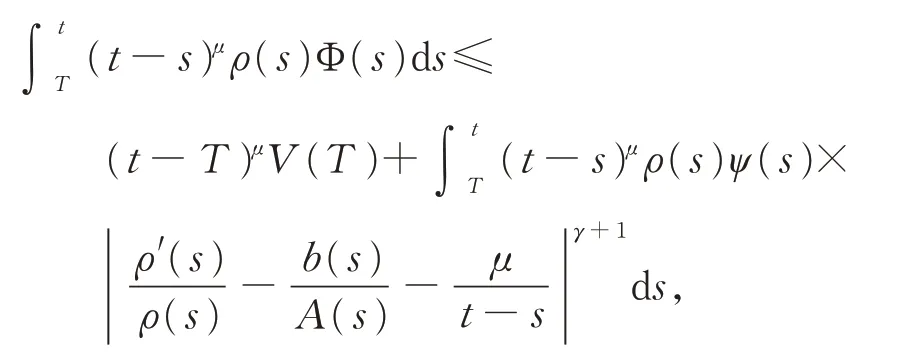
即

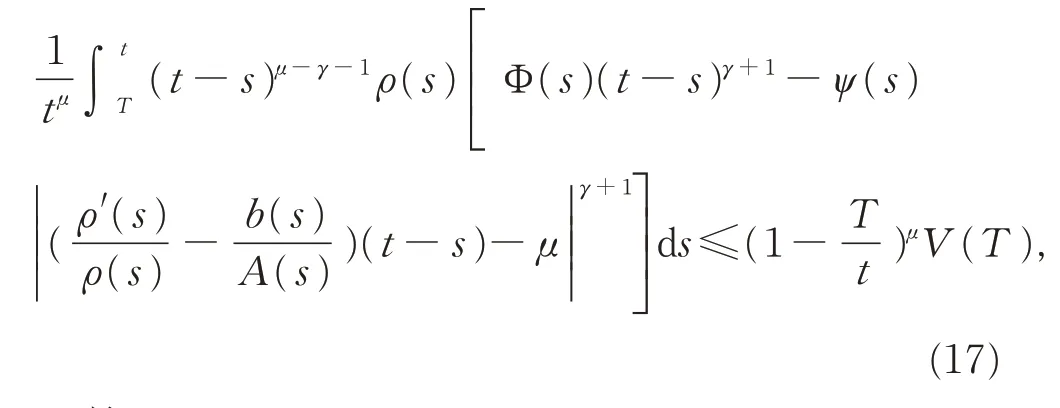
于是

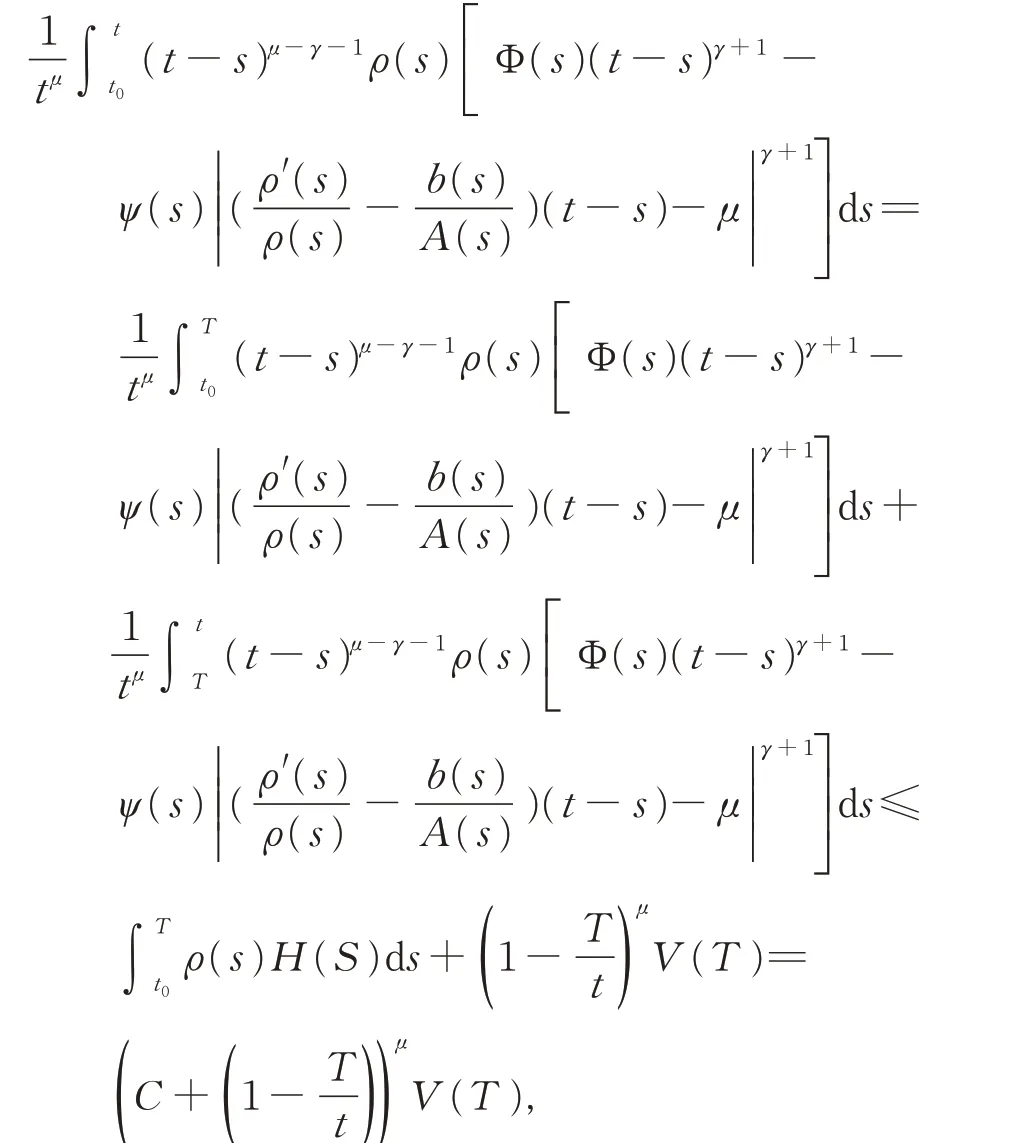
注 1若 方 程(1) 中 n=2，m=1，Pk(t)≡0，b(t)=0，Rj(t)≡0，f (u)=u，σ(t)=t，并在定理2 中取ρ(t)=1，于是由定理2，可得定理B。即定理A 和定理B 為定理2 的特例。此外，若方程(1)中，m=1，Pk(t)≡0，Rj(t)≡0，fi(u)=u，則定理1 即為文獻(xiàn)[11]中的定理2；進(jìn)一步，在定理2 中，取ρ(t)≡1，即得到文獻(xiàn)[11]中的定理1。關(guān)于方程(1)的特殊情形的不同振動(dòng)準(zhǔn)則，可參考文獻(xiàn)[5-11]。

注2若 方 程(1)中，n=2，h=m=l=1，b(t)≡0，γ=1，B(u)=u，τ(t)=t-τ0，σ(t)=t-σ0，δ(t)=t-δ0，則相應(yīng)地，本文定理1 和定理2 即為具有正負(fù)系數(shù)的二階微分方程(E4)的振動(dòng)準(zhǔn)則，但本文沒有文獻(xiàn)[4]的條件:“R(t)最終為負(fù)”，因此本文結(jié)果進(jìn)一步改進(jìn)并拓展了現(xiàn)有的研究成果。

例1考慮以下4 階具有正負(fù)系數(shù)的變時(shí)滯方程

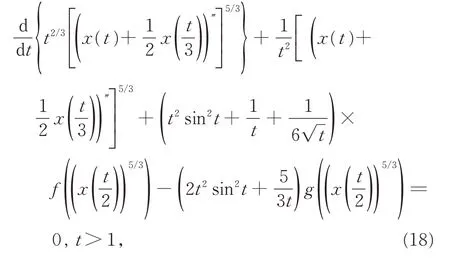
其中f,g 分別為f (u)=u[6+lnγ(1+u2)]，g(u)=這相當(dāng)于方程(1)中

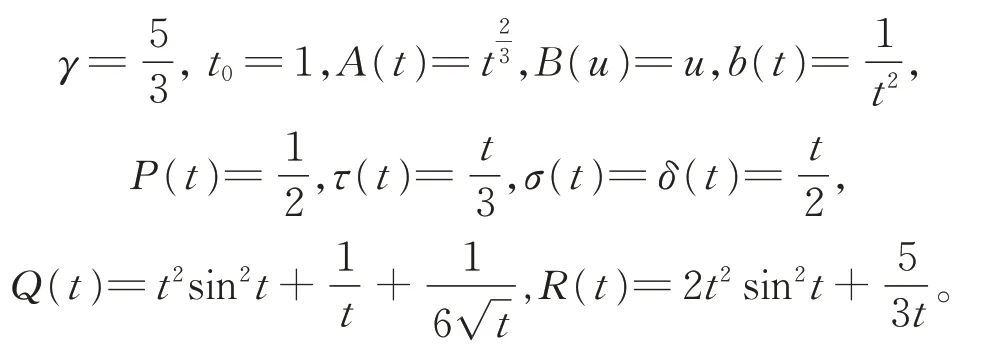
顯然有

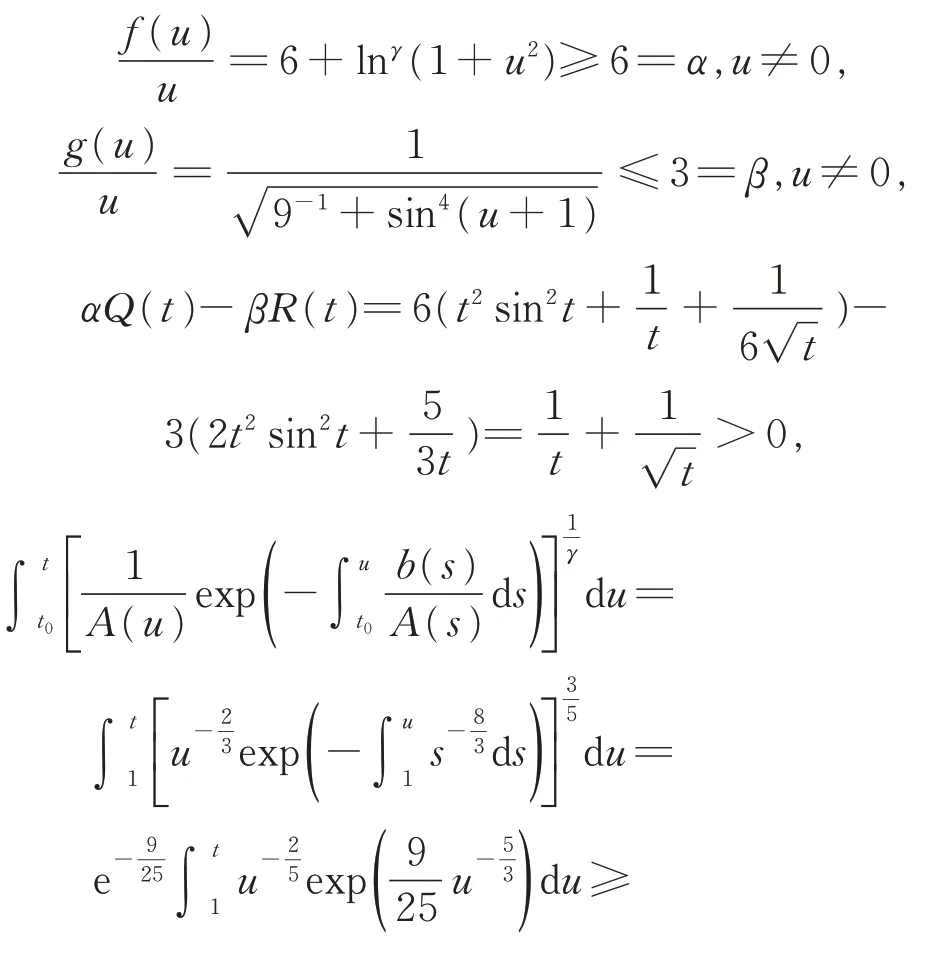
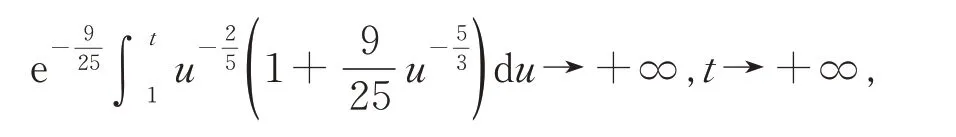
即條件(H0) ～(H5)成立。在定理1 中,取ρ(t)=1，并注意到式(9)，則有

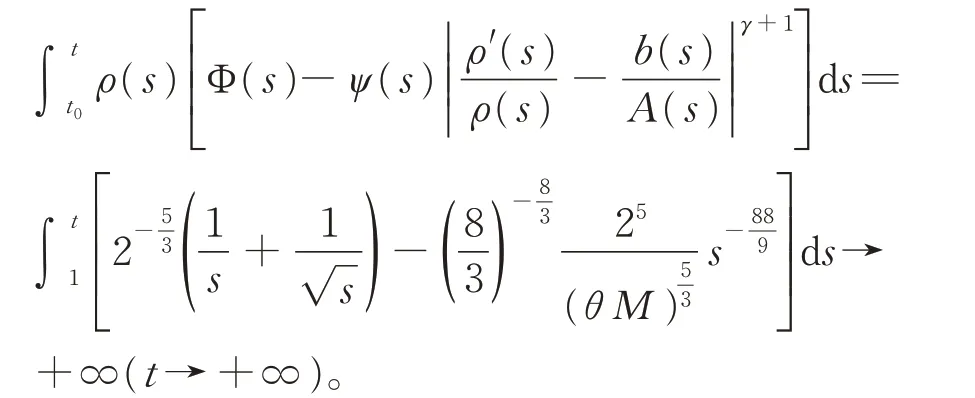
于是由定理1 知，方程(18)振動(dòng)。

例2考慮具有正負(fù)系數(shù)和阻尼項(xiàng)的變時(shí)滯2階方程

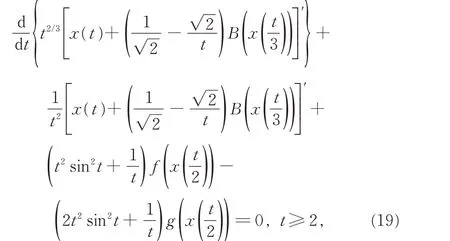
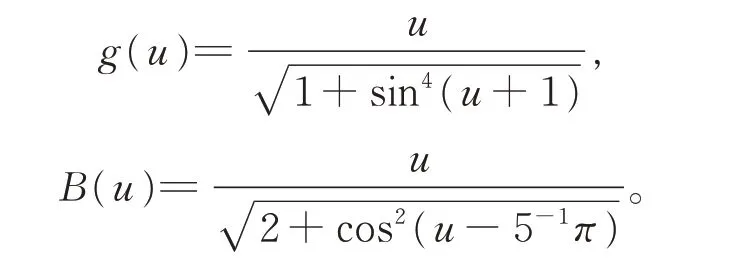
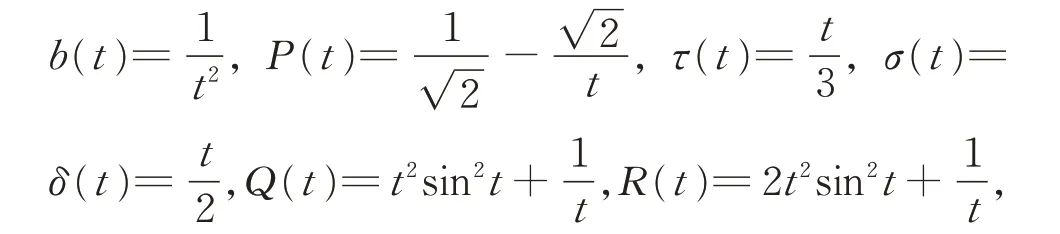
則

即 條 件(H0) ～ (H5) 成 立。 現(xiàn) 在 定 理2 中，取ρ(t)=1，μ=2 ＞γ，并注意到式(9)，則有

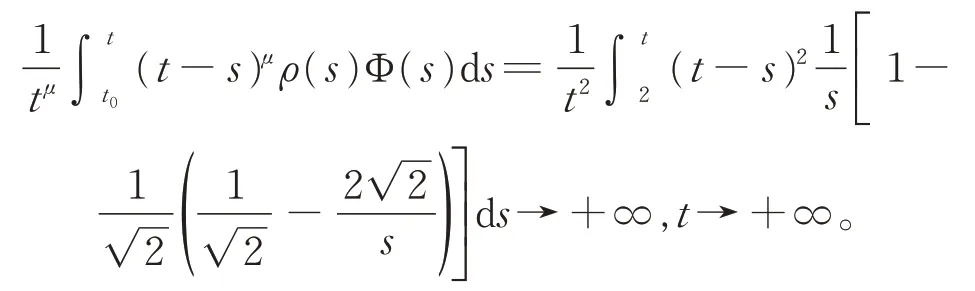
而

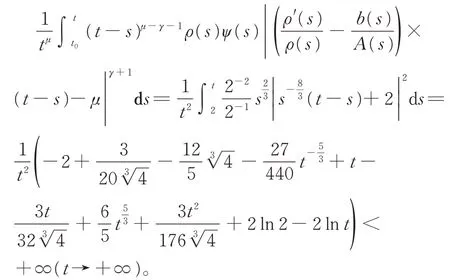
所以

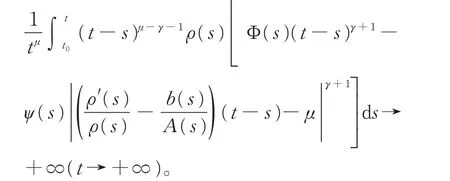
于是由定理2 知，方程(19)振動(dòng)。顯然文獻(xiàn)[1-12]中的定理均不能用于方程(18)和(19)的振動(dòng)性判別。