一類完全四階邊值問題解的存在性

陳雪春，李永祥

（西北師范大學數學與統計學院，甘肅 蘭州730070）

考慮完全四階邊值問題(BVP)

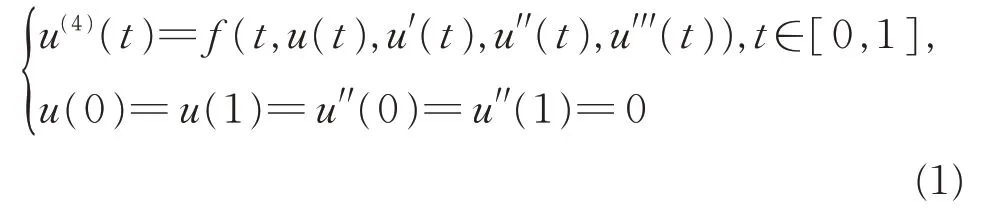
解的存在性，其中f:[0,1]×R4→R 為連續函數。邊值問題(1)描述了兩端簡單支撐的靜態彈性梁形變的數學模型。其中u′(t)表示隅角，u′(t)表示彎矩，u′′(t)表 示 剪 切 力 剛 度，u(4)(t)表 示 密 度 剛 度。根據兩端點的受力情況，這種描述又被分為若干類型的邊值問題。而問題(1)在物理學中有重要的理論意義，得到了該類問題特殊情形的一些結果[1-13]。

對非線性項不含任何導數項的簡單四階邊值問題：

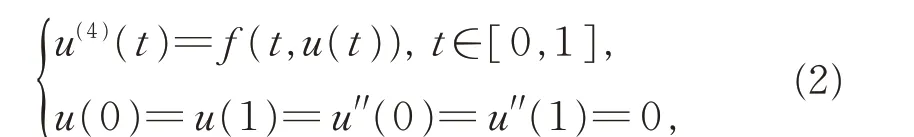
已有一些研究成果[1－4]。

對非線性項僅含彎矩項u′(t)的特殊四階邊值問題：

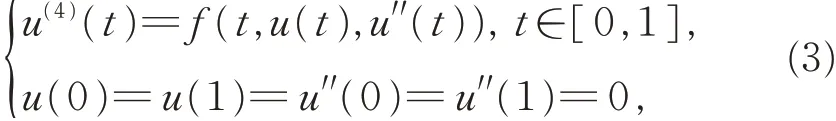
文獻[5-8]在非線性項滿足適當的增長條件下，運用不動點定理獲得了BVP(3)解的存在性。文獻[9-10]運用上下解方法討論了BVP(3)解的存在性。文獻[11-12]在非線性項非負的情形下，運用錐上的不動點指數理論和Krasnoselkii 不動點定理討論了BVP(3)正解的存在性。

對完全四階邊值問題(1)，由于u′(t)與u′′(t)變號引起的困難，上述研究特殊邊值問題(3)的方法不再適用，已有的研究工作很少。只有LI 等[13]在邊值問題(1)的非線性項滿足一次增長條件下運用Leray-Schauder 不動點定理研究了BVP(1)解的存在性和唯一性。

受上述研究的啟發，本文將文獻[9-10]中關于邊值問題(3)的上下解方法推廣到一般邊值問題(1)。相比已有研究，本文對非線性項的增長條件不作任何限制，也不假定非負的情形，在f (t,x0,x1,x2,x3)關于x3滿足Nagumo 型條件下，運用截斷函數技巧和上下解方法討論了BVP(1)解的存在性。

1 主要結果

定義1設v0(t)∈C4(I)，若v0(t)滿足

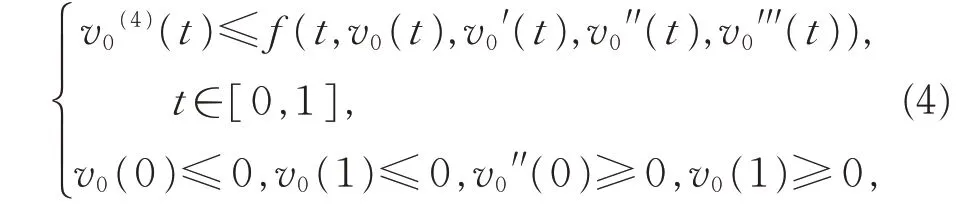
則稱v0(t)為邊值問題(1)的下解。若式(4)中均取反向不等式，則稱其為上解。

定理1設f:[0,1]×R4→R 為連續函數，BVP(1)存 在 下 解v0及 上 解w0，w0′≤v0′。若f 滿 足 下 列條件：

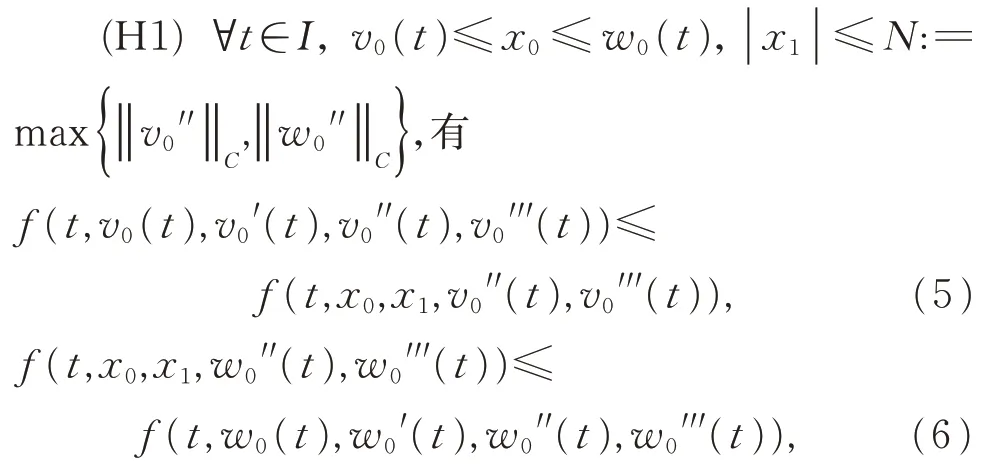
(H2) 存在[0,∞)上的正值連續函數H(ρ)，滿足

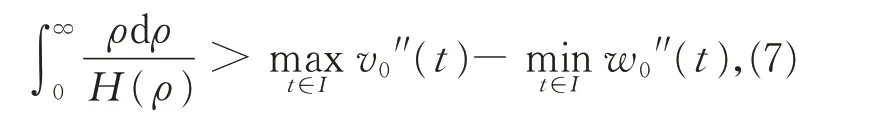
使得

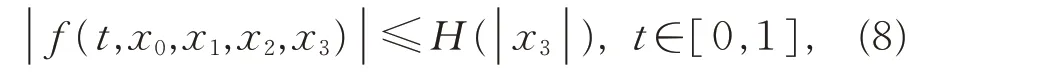
其中，

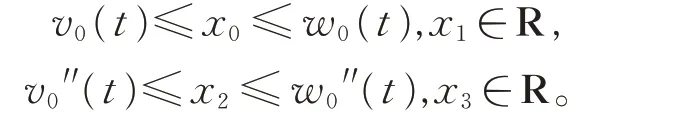
則BVP(1)至少存在1 個解滿足v0≤u ≤w0,w0′≤u′′≤v0′′。

2 預備知識

記I=[0,1]，C(I)表示定義在I 上的全體連續函數按范數構 成 的Banach 空間，對?n ∈N,Cn(I)表示定義在I 上的全體n 階連續可 微 函 數 按 范 數構成的Banach 空間。

引理1設v0,w0∈C4(I)分別為完全四階邊值問題(1)的下解與上解。若v0′′≥w0′′，則v0≤w0。

證明令u(t)=w0(t)-v0(t)，則有

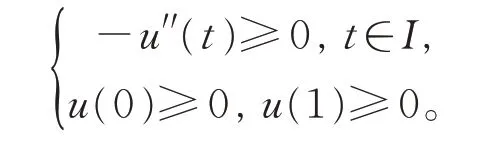
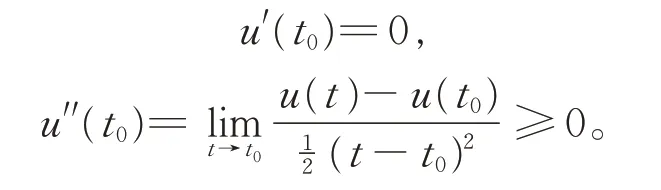
由中值定理可知，存在t1∈[a,t0)及t2∈(t0,b]，使得

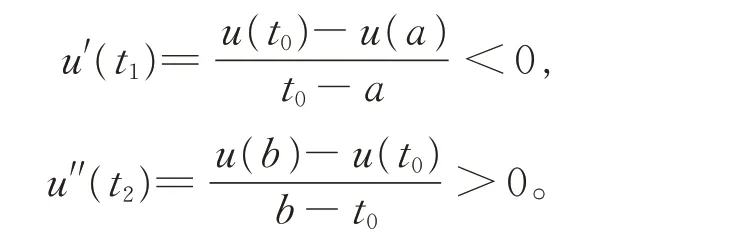
再對u′(t)用中值定理，存在t3∈(t1,t2)，使得

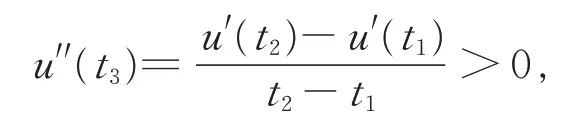
引理2設

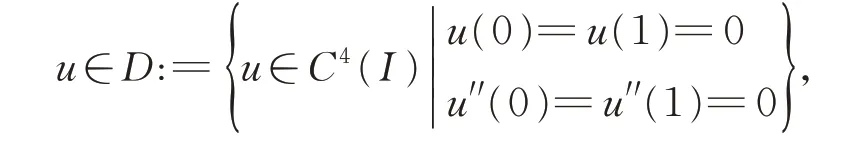
滿足w0′′≤u′′≤v0′′，則

證明對?u ∈D,t ∈I，有

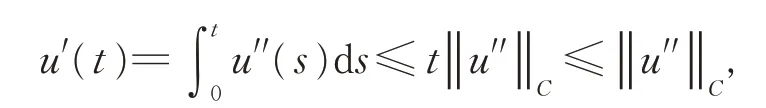
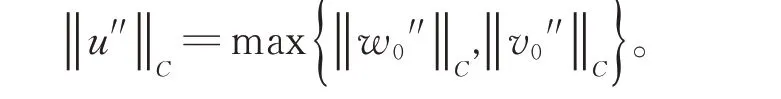
因此

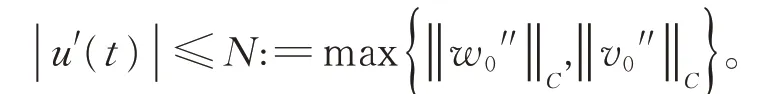
引 理 3設 f ∈C(I×R4,R) 連 續。 對存 在 常 數 ai≥0,i=0,1,2,3，和C ＞0,使得a0+a1+a2+a3＜1，并且f 滿足

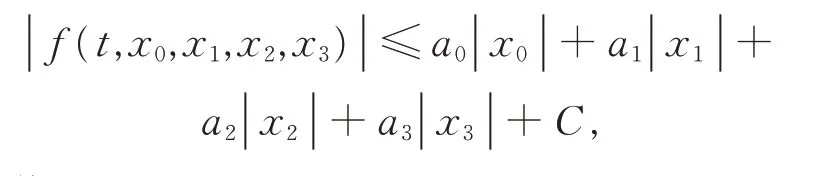
則邊值問題(1)至少有1 個解。

該引理的證明可參見文獻[13]定理1。

3 主要結果的證明

定理1 的證明由假設(H2) 的式(7)知，存在M ＞0，使得

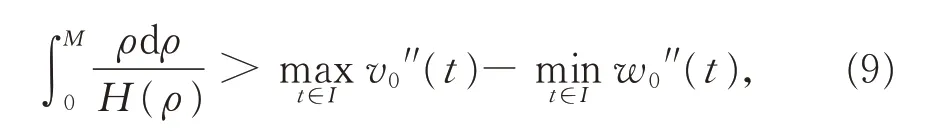
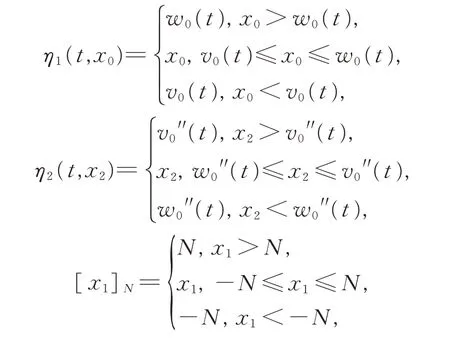
則函數η1，η2：I×R →R 連續，且滿足

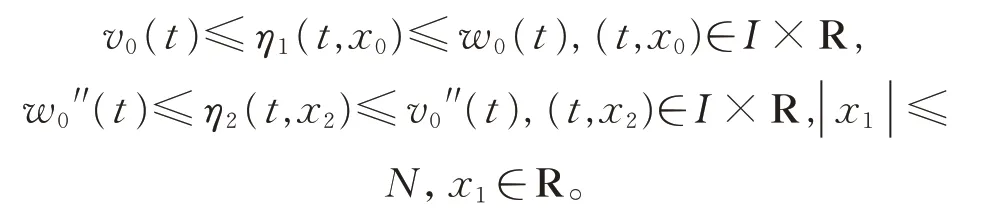
作f (t,x0,x1,x2,x3)的截斷函數

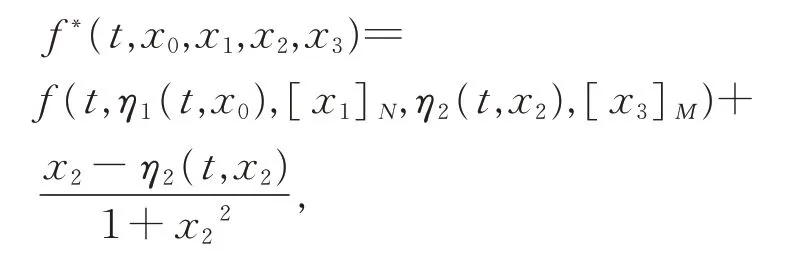
則f*:I×R4→R，連續有界。

由引理3，修改后的邊值問題

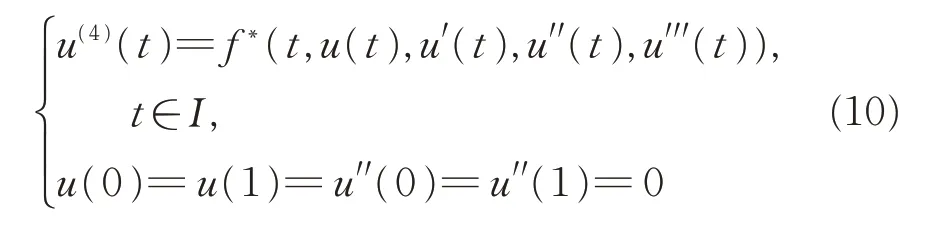
有解，u0∈C4(I)。

下證w0′≤u0′′≤v0′′。

先 證u0′≤v0′。 反 設u0′′＞v0′。 考 查 函 數φ(t)=v0′′(t)-u0′′(t)， t ∈I。 由 于 φ(0)≥0，φ(1)≥0，因此φ(t)＜0，則存在t0∈(0,1)，使得

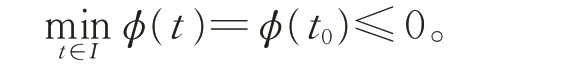
按最小值點的性質φ′(t0)=0，φ′(t0)≥0，可得

根據定義1 和式(5)有

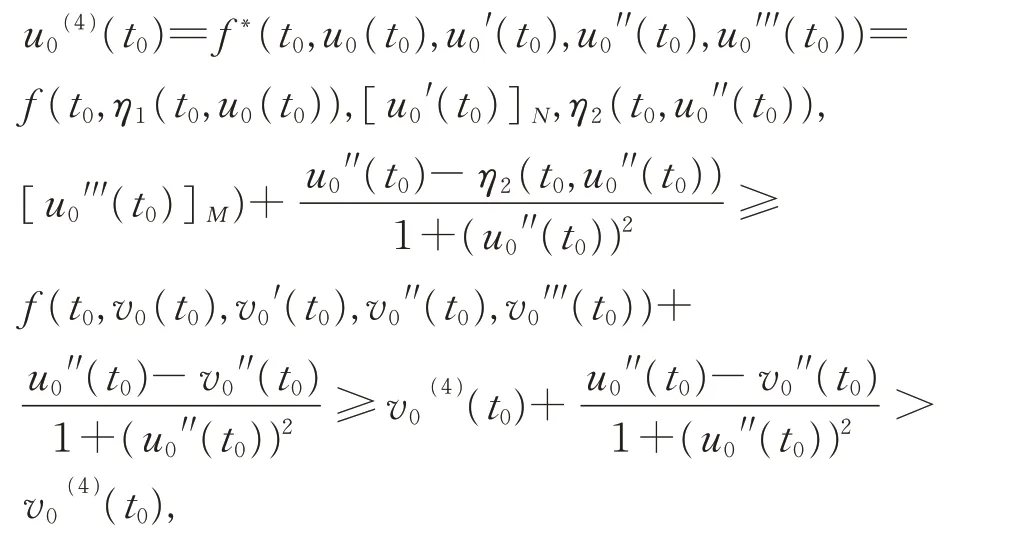
與式(11)矛盾!因此

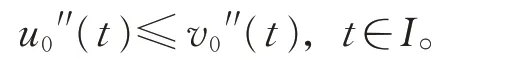
由引理1 可知，v0(t)≤u0(t)≤w0(t)，t ∈I。由引理2 知，|u0′(t)| ≤N，t ∈I。

再 證|u0′′(t)| ≤M，t ∈I。反 設|u0′′(t)|＞M，由中值定理可知，?t1∈[0,1]，使得u0′′(t1)=0。由最大值定理，存在t2∈[0,t1)或t2∈(t1,1]，使得

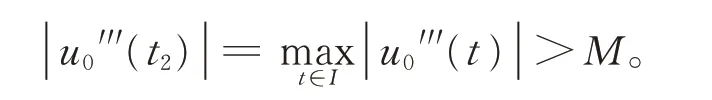
下分4 種情形證明：

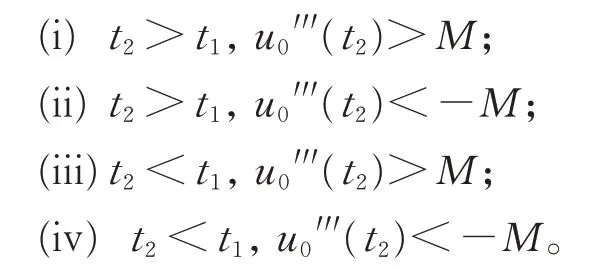
情形(i)（其他情形類似可證），令

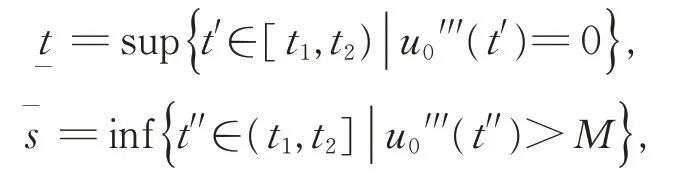
由u0′′(t)的 連 續 性 及 上 下 確 界 的 定 義 可 知，t1≤且

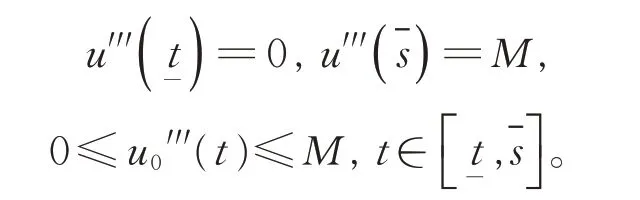
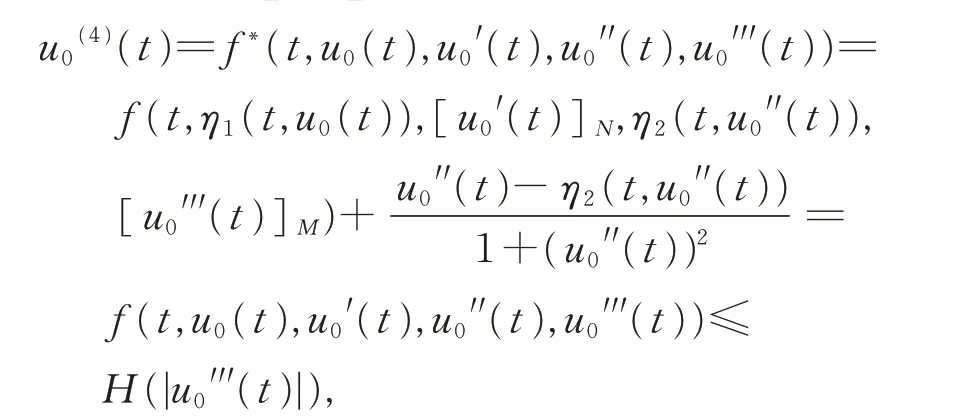
由 于u0′′(t)＞0，上 式 兩 邊 同 乘u0′′(t)，并 在上積分，可得

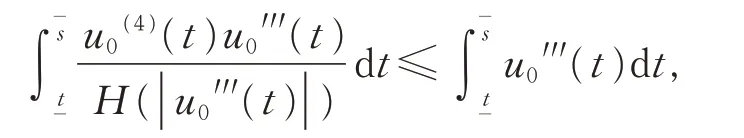
令ρ=u0′′(t)，則有

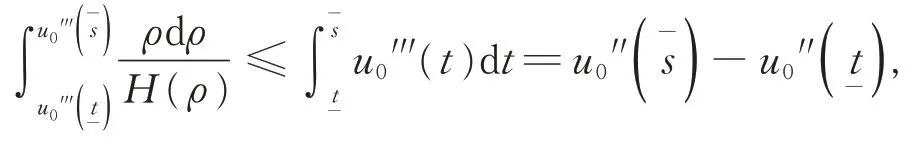
即

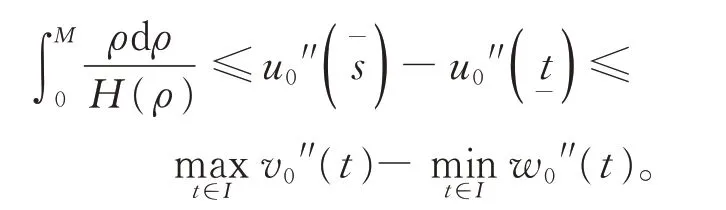
與式(9)矛盾!故|u0′′(t)| ≤M，t ∈I。

因此，按f*的定義，有

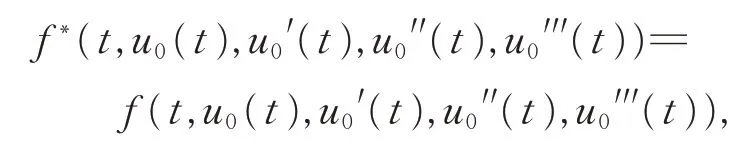
故u0(t)為BVP(1)的解。

例1 考慮完全四階邊值問題:

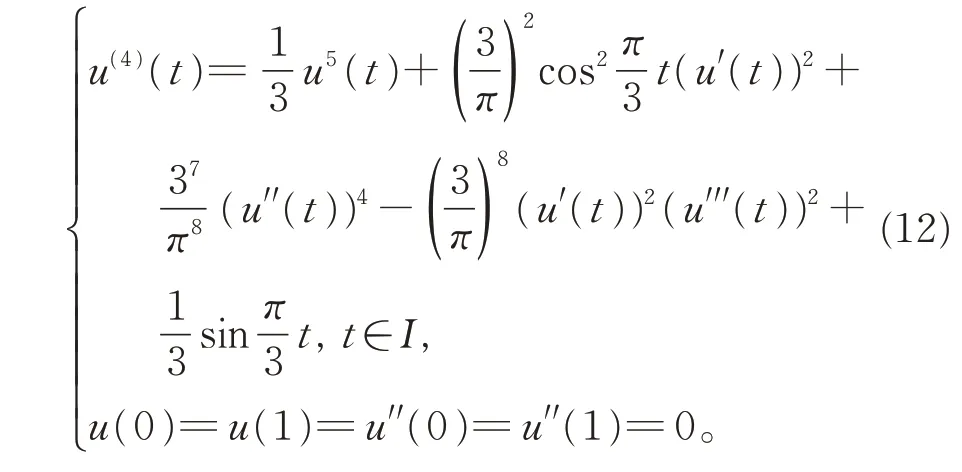
相應地，非線性項為

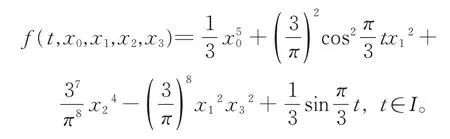
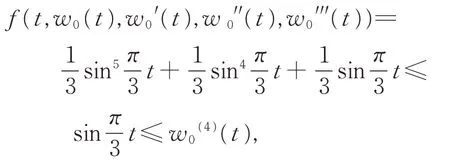
所以w0(t)為邊值問題(12)的上解。

下證f 關于v0，w0滿足條件(H1)，(H2)。

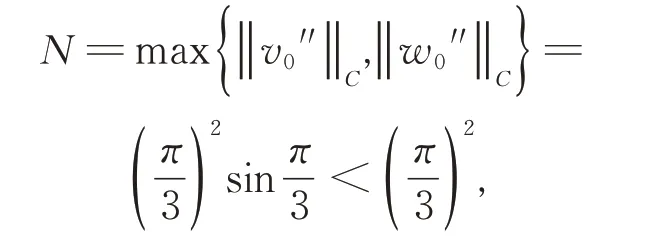
所以當0 ≤x0時，

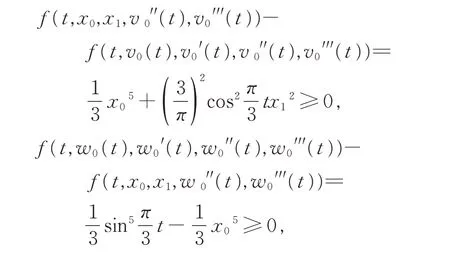
因此,f 滿足條件(H1)。

又因為f (t,x0,x1,x2,x3)關于x3是二次增長的，易取二次增長函數H(ρ)使得f 滿足條件(H2)。由定理1，方程(12)至少有1 個解u，滿足