考慮實時擁堵指數和時間窗的多目標冷鏈物流配送路徑優化

摘要：針對生鮮產品冷鏈物流配送時間和總成本最小化為目標，對配送中車輛使用成本、油耗以及碳排放成本等進行綜合考慮。在實時擁堵指數和配送時間窗的約束下，構建成本最小化模型。并結合行駛過程中三個連續階段的擁堵指數導致的行駛時間變化，從而得到優化策略;最后，基于Pareto支配接受準則的多目標模型進行求解，通過實際案例驗證了模型的實用性和算法的有效性。結果表明，通過減少成本以及縮短時間來滿足客戶需要，將滿足國家以及人民對冷鏈物流配送的要求。

Abstract： Aiming at minimizing the distribution time and total cost of cold chain logistics of fresh products， the vehicle use cost， fuel consumption and carbon emission cost are considered comprehensively. Under the constraints of real-time congestion index and distribution time window， a cost minimization model is constructed. The driving time caused by the congestion index in three consecutive stages during the driving process is combined to obtain an optimized strategy. Finally， the multi-objective model based on Pareto domination acceptance criterion is solved， and the practicability of the model and the effectiveness of the algorithm are verified by a real case. The results show that by reducing costs and time to meet customer needs， it will meet the national and people's requirements for cold chain logistics distribution.

關鍵詞：冷鏈物流;實時擁堵指數;路徑優化;模擬退火算法

Key words： cold chain logistics;real-time congestion index;path optimization;simulated annealing algorithm

中圖分類號：F259.2;X322? ? ? ? ? ? ? ? ? ? ? ? ? ?文獻標識碼：A? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 文章編號：1006-4311（2020）09-0131-03

0? 引言

隨著經濟的發展和居民生活質量的提高，人們對生鮮產品的需要也越來越高，同時對冷鏈物流的要求也越來越高。與傳統的物流相比，冷鏈物流對運輸產品的時效性具有更高的要求，此外，在考慮成本的情況下，也應降低行駛過程中對于車輛以及冷凍設備等產生的碳排放量。因此，本文在確保生鮮產品時效性的前提下，實現低碳運輸，建立冷鏈物流配送模型。

1? 問題的描述與模型建立

1.1 問題描述

已知L連鎖超市生鮮配送中心的冷鏈配送車輛為同一車型，且車輛最大載重為Q，配送車輛以L連鎖超市生鮮配送中心為起點，執行完配送任務后且再返回L連鎖超市生鮮配送中心。假設L連鎖超市的每個超市被且只被訪問一次，配送車輛的最大裝載量不能超過配送車輛的最大載重量Q，每個需被配送的超市都有一個時間窗，且不允許超過時間窗范圍。本文考慮道路的交通擁堵和滿足時間窗約束情況下，對冷鏈物流配送路徑優化問題進行研究，考慮碳排放最低和配送時間最短兩個目標。

1.2 假設前提

①配送網絡中，顧客的需求量已知;

②車隊只有一種運輸車輛，其參數已經確定;

③車輛在途中不允許停留，不考慮貨物裝卸時間;

④顧客的需求必須被滿足，并且顧客的需求不超過一輛車輛的總容量。

1.3 道路實時交通擁堵指數設置

根據車載GPS收集到的數據以及道路功能和流量等綜合因素，換算成實時擁堵指數指標，從而用數值方式量化描述道路交通運行狀態，提高道路交通運行狀態表達精度，同時也達到一個指數值。無論對快速路、地面主干路或其他道路具有相同的擁堵含義描述。為了能更有效及準確的收集各路段的實時擁堵指數，本文路段的實時擁堵指數來自于百度智慧交通，百度智慧交通是基于百度地圖海量的交通出行數據、車輛軌跡數據、位置定位數據挖掘計算所得，根據對各路段長久以來歷史數據的收集，可以準確的預測出各個時刻路段的實時擁堵指數。

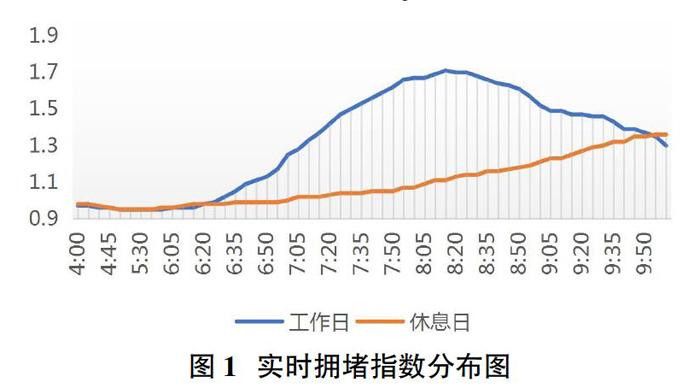
參考文獻及計算方法，為設置合理的擁堵參數，以上海市為例，通過百度地圖智慧交通數據，研究其交通擁堵情況，如圖1所示，因考慮生鮮配送時間，圖中僅研究從4：00-10：00的道路實時擁堵指數。

在模型計算中，根據周一至周五的擁堵指數按照以下標準規則，將實時擁堵指數與速度之間的關系對應起來，如表1。

1.4 參數變量

為了便于問題的求解，我們給出如表2所示符號說明。

1.5 車輛時間求解

1.5.1 實時擁堵指數變化時的行駛時間計算方法

一般擁堵情況下的行駛時間模型，在行駛過程中大致分為三個連續階段：①擁有穩定速度vncon（變量）的正常行駛期，②擁有穩定速度vcon （常量）的擁堵期，③在兩者之間的過渡期。車輛在行駛弧的距離d和離開時間l的計算如下式子所示：

上述式子中分別對應的行駛狀況如下：式1）和式5）表示車輛處于正常自由行駛情況;式2）表示車輛處于由正常過渡到擁堵情況;式3）表示車輛處于完全擁堵的情況;式4）表示車輛處于由擁堵過渡到正常自由行駛的情況。

1.5.2 總行駛時間計算

在時變交通擁堵狀況下，為了確定車輛在行駛弧（i，j）上的總行駛時間Tij，引入一個非負變量t■■表示

1.6 車輛成本求解

1.6.1 車輛的固定使用成本（人力成本+車輛使用成本）

使用車輛的固定成本通常是常數，與車輛行駛里程和服務的顧客數量沒有關系，包括車輛的固定損耗以及駕駛員工資等與車輛使用相關的成本，設定為常數C1。

其中，Sk為0，1變量，Sk=1表示配送中心第k輛車被使用，否則Sk=0。

1.6.2 油耗（運輸成本）和碳排放成本

為定量研究車輛燃油消耗和碳排放的計算，客戶節點（i，j）的單位距離燃油消耗量ρ與車輛載重量Qx成線性關系可表示為：

已知配送車輛自重Q0，最大載重量Qk，設空載時單位距離燃油消耗量ρ0，滿載時燃油消耗量ρ*，所以有：

得出：

可以得出，單位距離車輛燃油消耗量為：

可以得出客戶節點（i，j）路段配送中所產生的燃油成本C2和配送中總碳排放量Qc表示為：

碳排放成本主要是描述車輛在配送過程中產生碳排放量的環境成本，本文通過燃油消耗來刻畫車輛碳排放量，通過碳稅機制定量計算碳排放成本，即碳排放成本=碳稅*碳排放量，則在客戶節點配送中的碳排放成本C3表示為：

1.7 目標函數模型

式（1）為目標函數1，代表車輛配送時間最短。式（2）為目標函數2，代表總的配送成本最小。式（3）為車輛運載能力約束。式（4）為配送車輛數量約束。式（5）為每輛車的配送線路起點和終點都是配送中心。式（6）和式（7）表示每個客戶都需要被訪問一次且只被訪問一次。式（9）和式（10）是時間窗約束。

2? 模擬退火算法

多目標優化方法：

通過對模型的分析，發現該模型有兩個目標函數，時間最短和總成本最小。為求得多目標優化問題的非劣解常常需要將多目標優化問題轉化為單目標優化問題去處理，實現這種轉化，的經典方法主要有加權法，∈-約束法，進化算法等。多目標形式如下：

其中k？叟2表示目標函數同時最小化。本文是一個k=2的雙目標優化問題采用以下形式：

為了產生盡可能多的生成 Pareto 最優解，每當右側∈j有少量增加，問題也再次求解。因此，首先選擇最小化總行駛時間為目標函數進行優化求解，然后把得到的總時間作為約束條件，對第二個目標函數進行優化求解。

3? 算例求解

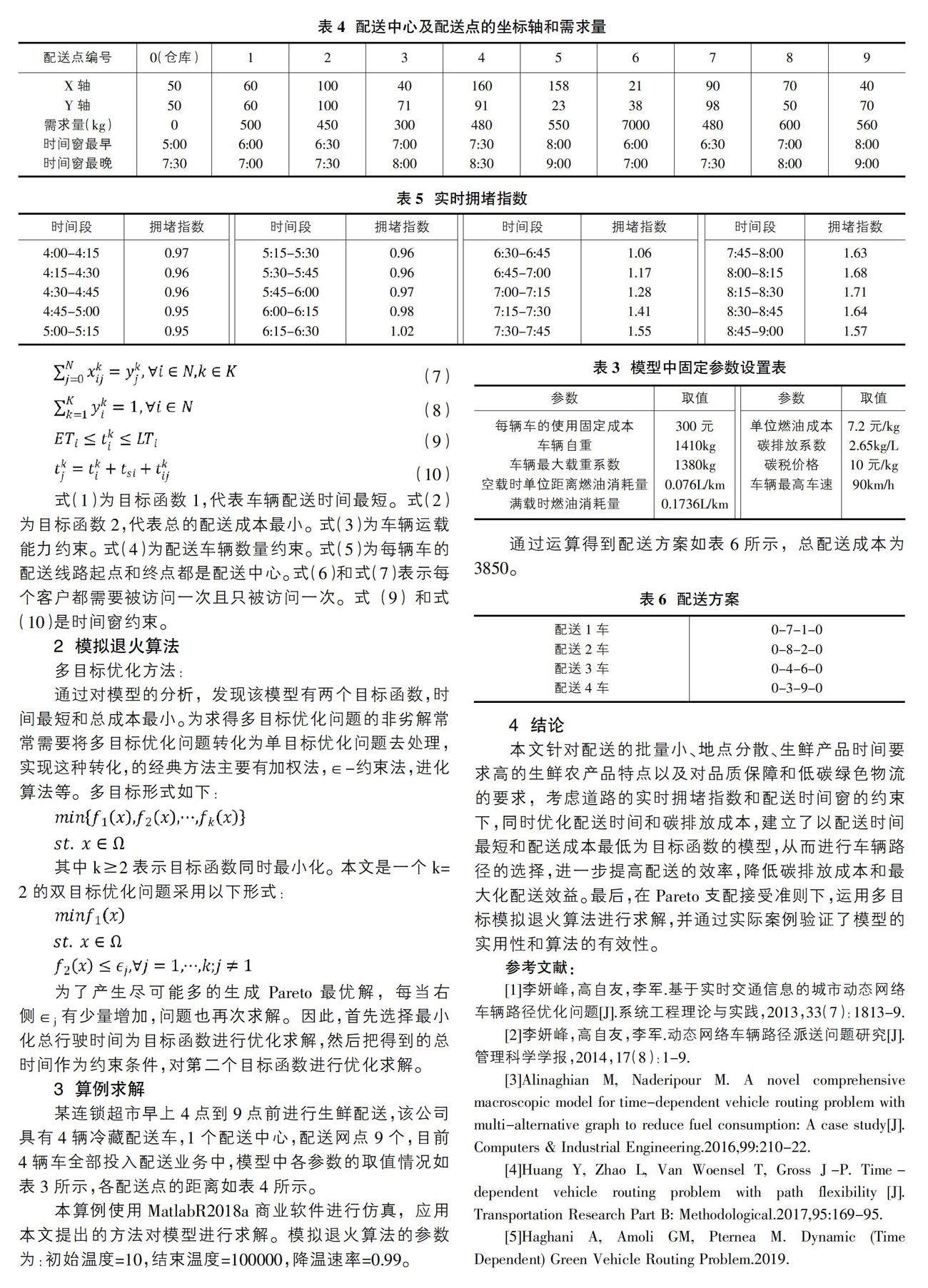
某連鎖超市早上4點到9點前進行生鮮配送，該公司具有4輛冷藏配送車，1個配送中心，配送網點9個，目前4輛車全部投入配送業務中，模型中各參數的取值情況如表3所示，各配送點的距離如表4所示。

本算例使用MatlabR2018a商業軟件進行仿真，應用本文提出的方法對模型進行求解。模擬退火算法的參數為：初始溫度=10，結束溫度=100000，降溫速率=0.99。

通過運算得到配送方案如表6所示，總配送成本為3850。

4? 結論

本文針對配送的批量小、地點分散、生鮮產品時間要求高的生鮮農產品特點以及對品質保障和低碳綠色物流的要求，考慮道路的實時擁堵指數和配送時間窗的約束下，同時優化配送時間和碳排放成本，建立了以配送時間最短和配送成本最低為目標函數的模型，從而進行車輛路徑的選擇，進一步提高配送的效率，降低碳排放成本和最大化配送效益。最后，在Pareto支配接受準則下，運用多目標模擬退火算法進行求解，并通過實際案例驗證了模型的實用性和算法的有效性。

參考文獻：

[1]李妍峰，高自友，李軍.基于實時交通信息的城市動態網絡車輛路徑優化問題[J].系統工程理論與實踐，2013，33（7）：1813-9.

[2]李妍峰，高自友，李軍.動態網絡車輛路徑派送問題研究[J].管理科學學報，2014，17（8）：1-9.

[3]Alinaghian M， Naderipour M. A novel comprehensive macroscopic model for time-dependent vehicle routing problem with multi-alternative graph to reduce fuel consumption： A case study[J].Computers & Industrial Engineering.2016，99：210-22.

[4]Huang Y， Zhao L， Van Woensel T， Gross J-P. Time-dependent vehicle routing problem with path flexibility[J].Transportation Research Part B： Methodological.2017，95：169-95.

[5]Haghani A， Amoli GM， Pternea M. Dynamic （Time Dependent） Green Vehicle Routing Problem.2019.

作者簡介：吳欣（1995-），女，安徽宿州人，碩士在讀，研究方向為公路運輸。