基于GARCH族模型的比亞迪股票價格波動性研究

摘要：波動性是股票市場賴以存在和持續發展的重要理論基礎，股價的存在和波動是證券投資者能夠獲取穩定投資回報和收益的重要前提，對于證券市場的持續發展有著積極的影響。本文選取比亞迪股票日收盤價數據作為研究對象，運用Eviews軟件建立了基于GARCH族模型的比亞迪股票價格波動性分析模型。結果表明，EGARCH模型對數據的擬合性能最強，同時殘差序列符合t分布。這說明比亞迪股票價格存在波動的集群性，同時也佐證了比亞迪股票價格支撐風險溢出理論。

Abstract： Volatility is an important theoretical basis for the existence and sustainable development of the stock market. The existence and fluctuation of stock prices have a positive impact on the sustainable development of the securities market，and they are important prerequisites for securities investors to obtain stable investment profits and returns. This article selects BYD stock daily closing price data as the research object， and uses Eviews software to build a BYD stock closing price volatility analysis model based on the GARCH family model. The results show that the EGARCH model can fit the data most accurately， and the error follows the t distribution. The result indicates that there are clusters of fluctuations in BYD stock prices. The result also suggests that BYD stock prices follow the risk spillover theory.

關鍵詞：比亞迪股票;股價波動性;GARCH模型族;時間序列

Key words： BYD stock;stock volatility;GARCH model family;time series

中圖分類號：F224.0? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?文獻標識碼：A? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 文章編號：1006-4311（2020）09-0280-05

0? 引言

股票作為金融資本證券化的重要工具，代表了股票持有者對于虛擬股票資本的最終所有權。股票價格就是虛擬股票在二級證券交易市場上的實際交易價格，它作為一種有價證券的交易憑證，本身不一定具有價值，它之所以能夠具有這種價格，是因為股票能夠在二級證券市場上有效地流通。股票市場受社會和國家的政策、公司的發展等諸多宏觀市場因素的直接影響，股票價格產生的波動反映了股票市場最直接的性質和現狀。而價格波動性是股票市場綜合地反映了股票市場的各種價格波動所發現的性質和功能、衡量股票市場的狀況最簡潔和有效的指標之一。它不僅與股票市場的各種不確定性和市場的風險直接密切相關，在我國各類金融資產的市場定價與其他資產的配置中一直處于最重要和最核心的地位，更是市場經濟行為的重要邏輯基礎和決定衡量因素，是對市場成熟與否的一個關鍵和評判的標準，同時還是衡量一個國家和地區經濟的發展和市場狀況的重要晴雨表[1]。

近三十年來，我國多層次的資本市場初步形成和建立，股票市場雖然飛速發展，但市場規模、投資者審查、交易制度等方面仍然很不成熟，股票價格很容易而且常受到多種經濟因素（主要是含括該國經濟生存和發展的狀況、經濟的結構、消費者的結構等）和非經濟因素（主要泛指除了經濟因素之外的各種因素，包括企業生產力、所有制、經濟體制等）的直接影響，較之國外比較成熟、發達的多層次股票市場，我國多層次股票價格的實際波動性的最大幅度及其風險都很大。這種實際波動性往往意味著對股票未來市場價格的一種高度不可預測性或一種不確定性，給了投資者和企業帶來了股票投資決策上的許多困惑。由此，尋求找到一種理論上能夠較為真實、準確地刻畫并體現多層次股票價格的波動性和股票投資風險的經濟分析方法，是很多從事股票投資者和企業的經濟學家在進行探索和研究時所關心的一個重要問題[2]。

在多個國際金融研究領域，學者們通常都會選擇采用傳統的股指序列數據分析方法來預測和研究某一時期股票價格的周期變化及其趨向、走勢。以前研究股票價格序列多采用的方法是線性的時間序列假設，主要方法有隨機游走模型和ARMA（Auto-Regressive and Moving Average Model）模型，即自回歸滑動平均模型。在市場經濟研究中，ARMA模型常用于追蹤長期市場資料的研究。但隨著我國社會主義經濟的快速持續發展，金融市場中沖擊風險因素的增多，大多數的序列基本上是非線性的，傳統的金融市場ARMA的模型不能較為完整、準確地刻畫其風險因素分布序列的特征，因此ARCH的模型應運而生，特別是在其推廣后的GARCH的模型，能夠較好地準確刻畫金融市場股票價格的“厚尾”的基本特點。GARCH的模型不但準確刻畫、描述了金融市場的正負向沖擊對股票價格產生的影響是否具有非對稱性，而且在其研究諸如預期經營收益與金融市場預期經濟風險的對稱性關系上也同樣具有明顯突出的意義和作用。

1? 文獻綜述

1.1 國內外研究綜述

股票市場的波動性研究是現代證券業及金融學等各個領域的重大研究課題，而我國的股市作為全球范圍內不可預測性最強的股票交易市場之一，對其個股價格波動性的基礎研究也逐漸變得不可或缺。目前關于我國股市個股價格波動性的研究主要有兩個大的方向：一個是對于股票價格波動性有顯著影響的因素和因子的基礎研究;另一個問題是關于股票市場中個股波動性的性質以及一般規律的基礎研究。

在國外的研究領域中，ARCH模型已經作為一種統計性能良好的刻畫金融時間序列數據波動性的重要數據分析工具，被廣泛應用于與波動性密切相關的金融時間序列以及經濟時間序列研究。Vicent Arago-Manzana，Ma Angeles Ferna-Ndezizquierdo（2017）[3]使用GARCH模型研究了ESP-35股票指數波動性和指數收益率波動性的季節性規律。研究結果顯示該指數波動存在以月為單位的波動周期，而指數收益率則不具有直觀的波動周期。具有這種特征的時間序列通過傳統的經濟計量分析方法已經不能很好的描述和解釋，而運用ARCH模型就能夠很好的描述和分析此類問題。

在國內的研究領域中，ARCH模型在我國證券市場股票價格的波動性研究中扮演重要的角色。近年來我國不少專家學者選用ARCH族以及廣義化的GARCH族模型分析我國股票市場，閆冀楠、張維（1998）首次對上海證券交易所上市公司股價的收益分布特征和波動性進行實證分析;唐小鳳（2017）[4]，嚴定琪，李育鋒（2018）[5]利用ARCH類模型深入分析了我國股票市場的有效性，估計了我國股票市場的整體和系統金融風險，幫助政府擬定和完善金融政策等問題做了深入的實證分析研究。

1.2 本文創新點

本文以現代金融理論為指導思想和方法論，應用符合有效市場假說的GARCH模型族對比亞迪股票價格的波動性進行研究，與以往的研究相比較：

①本文使用GARCH族模型著重分析了比亞迪股價在2年內的股價波動，GARCH模型族對于金融資產價格的波動性有很好的實證分析效果和預測性能，特別是在股票市場波動性上已經得到了廣泛的應用，同時，相比于選取長期時間序列數據進行研究，這樣更能刻畫比亞迪股票在短周期內的波動特征。

②在以往的研究中，更多的論文重點在于用某一種模型分析樣本數據的波動特征，而本文從多個模型的角度分析同一組數據，可以從該組數據得到更多樣的波動特征。

③本文從多種模型中選取出更擬合該組數據特征的模型，將當前一切可利用信息作為條件，對比亞迪股票2年內的股價波動進行實證分析，為探究異常波動的原因提供了線索。

2? 模型建立與實證分析

2.1 ARCH模型的起源

對于某個風險資產的時間序列，我們想要建立特質化的模型并用新的方法去推演其未來不確定性的波動通常有如下幾個的原因：首先，我們可能需要重新分析我們持有某項風險資產的不確定性以及其置信區間;其次，預測的殘差方差可能并不是一成不變的，也即該序列具有異方差性，所以我們可以通過建立新的殘差方差的模型得到更符合事實的置信區間;第三，如果殘差的異方差是有可能得到適當控制的，我們就可能得到更有效的風險估計。

針對條件異方差時間序列而構造的特質化時間序列模型隨之應運而生，即自回歸條件異方差（Autoregressive Conditional Heteroscedasticity Model， ARCH）模型。ARCH模型最初是1982年由恩格爾（Engle， R.）提出，并由博勒斯萊文（Bollerslev， T.， 1986）發展成為GARCH（Generalized? ARCH）——廣義自回歸條件異方差。ARCH族以及GARCH族模型由于具有出色的對條件異方差數據的擬合與預測性能，被廣泛的運用于經濟學和金融學的實證研究領域，其中在金融時間序列分析中的運用最為普遍。

2.2 數據選取及處理

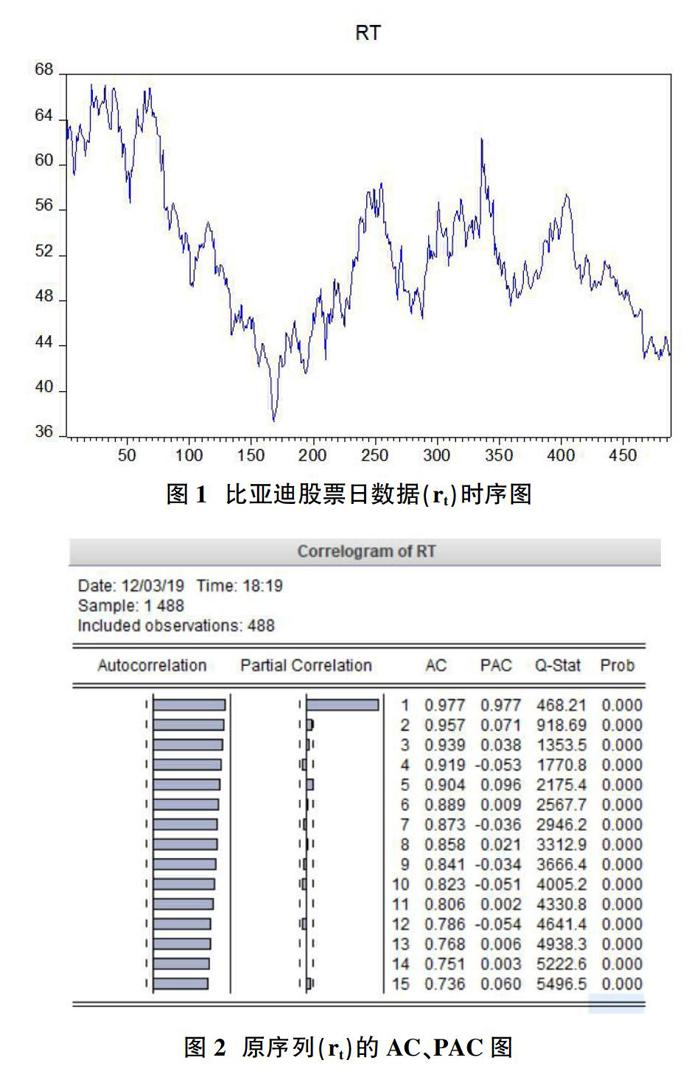
選取比亞迪股票（股票代碼002594）2017年11月29日至2019年11月29日的日收盤價數據作為研究對象。由于該股票并非每日均可能有準確的交易數據，所以也并非每日均有收盤價，因此該數據有缺失值，只能作為非平衡數據進行分析。我們將2017年11月29日至2019年11月29日可收集的488個數據的時序命名為1-488，用Eveiws畫出比亞迪股票日收盤價數據的時序圖、自相關以及偏自相關圖。為了便于表達，我們將比亞迪股票原序列記為rt，并將rt通過一階差分形成的新序列記為drt。

由比亞迪股票價格（rt）的AC圖可以看出，其價格的自相關性過強，序列顯然不平穩，不適合建模。因此，需要先對原數據進行處理。我們考慮先對其進行一階差分，并觀察其差分項（drt）的形態。

接著觀察序列的自相關性，如圖4。

從圖中可以明顯看出，序列的自相關和偏自相關系數均落入兩倍的估計標準差置信區間內，且Q-統計量的值均顯著，故序列在5%的置信度下不可能存在顯著的自相關性。對drt序列進行ADF平穩性檢驗，如表1所示。

t統計量的值-23.79，對應P值非常接近0，表明序列drt平穩。我們也可以直觀地認為比亞迪股票收盤價通過一階差分所形成的新序列趨于平穩，適合于建立模型。

2.3 ARCH效應檢驗

在我們建立GARCH模型之前，我們通常需要先對序列drt進行ARCH效應檢驗。表2所示為序列drt的描述性統計量。

構建一個變量殘差圖5為殘差平方項z的相關圖，可以直觀地看出在所有的滯后階數所對應的自相關和偏自相關系數皆不為0，且Q-統計量均顯著，所以該殘差序列存在ARCH效應。因此我們可以考慮先對drt建立GARCH模型。

2.4 GARCH模型

上述公式中，為{yt}的回歸函數;E（et）=0，Var（et）=1。p是移動平均ARCH項的階數，q是自回歸GARCH項的階數，p>0并且？茁i？叟0，1？燮i？燮p，？琢L和？茁L是滯后算子多項式。為了使GARCH（q，p）模型的條件方差有明確的定義，相應的ARCH（∞）模型的所有系數都必須是正數[6]。

GARCH建模：

常用的GARCH模型包括GARCH（1，1），GARCH（1，2），GARCH（2，1），GARCH（2，2），我們分別用多個模型建模，對比參數和顯著性，來建立適當的模型。

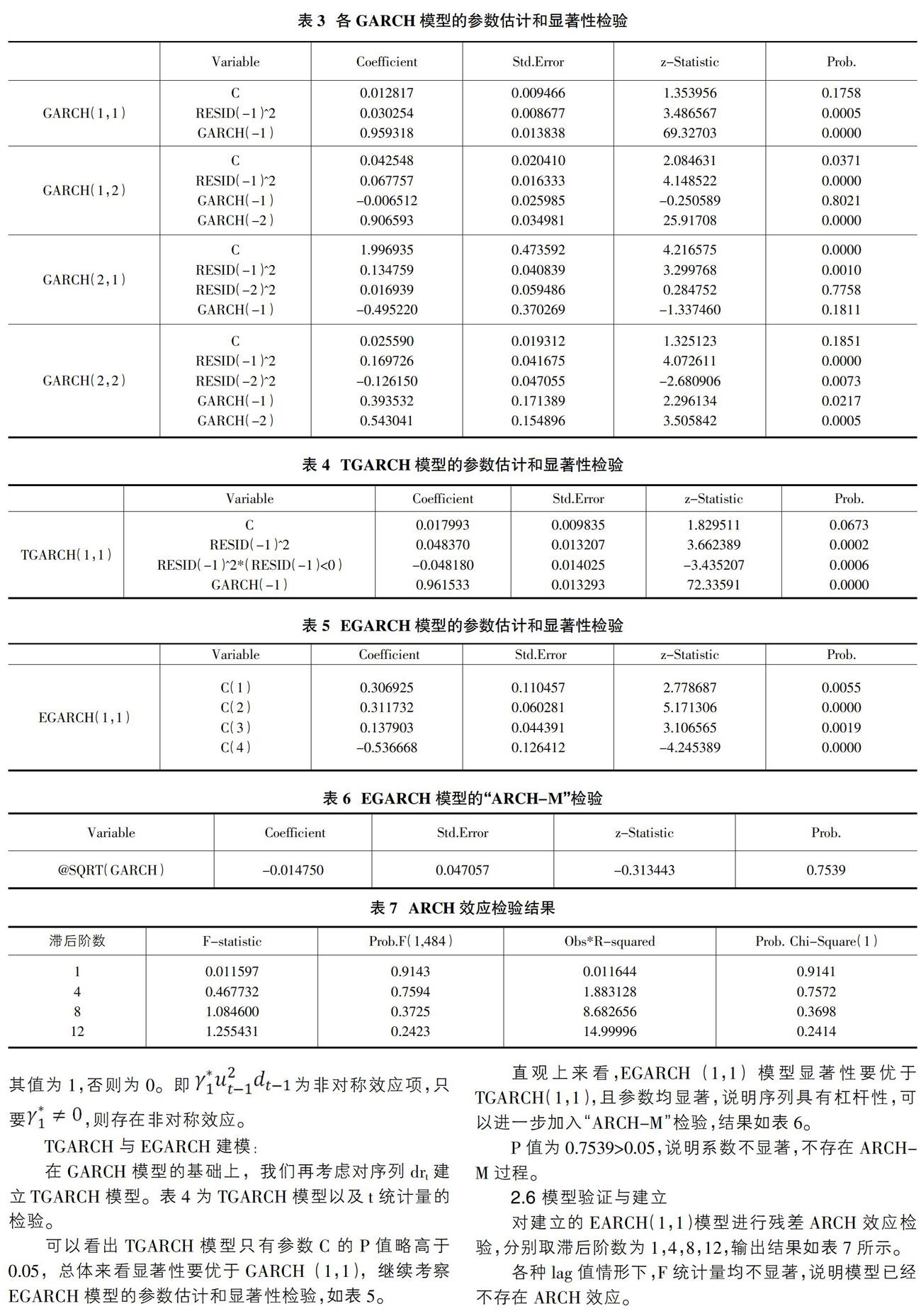
對殘差序列w進行GARCH模型擬合以及t統計量的檢驗，結果如表3。

基于以上四個模型的比較，GARCH（1，1）除了系數C以外，所有的系數都通過t檢驗，效果最好。再考慮TGARCH和EGARCH并分別進行建模。

2.5 TGARCH和EGARCH模型

為了更精確地描繪股票市場杠桿效應以及正干擾和負干擾對股票價格波動影響的非對稱性，由GARCH族模型衍生出了一系列模型，如EGARCH、TGARCH和 PARCH模型，這些模型主要是對方差效應方程進行了拓展。其中TGARCH模型由Zakoian（1990）以及Glosten，Jaganathan和Runkle（1993）在GARCH模型的基礎上提出 [7]。以 TARCH（1，1）模型為例，該模型中的條件方差被設定為：

其中，dt-1是一個虛擬變量，當均值方程中的ut<0時，其值為1，否則為0。即為非對稱效應項，只要，則存在非對稱效應。

TGARCH與EGARCH建模：

在GARCH模型的基礎上，我們再考慮對序列drt建立TGARCH模型。表4為TGARCH模型以及t統計量的檢驗。

可以看出TGARCH模型只有參數C的P值略高于0.05，總體來看顯著性要優于GARCH（1，1），繼續考察EGARCH模型的參數估計和顯著性檢驗，如表5。

直觀上來看，EGARCH（1，1）模型顯著性要優于TGARCH（1，1），且參數均顯著，說明序列具有杠桿性，可以進一步加入“ARCH-M”檢驗，結果如表6。

P值為0.7539>0.05，說明系數不顯著，不存在ARCH-M過程。

2.6 模型驗證與建立

對建立的EARCH（1，1）模型進行殘差ARCH效應檢驗，分別取滯后階數為1，4，8，12，輸出結果如表7所示。

各種lag值情形下，F統計量均不顯著，說明模型已經不存在ARCH效應。

建立的EGARCH（1，1）模型如下：

3? 結論

本文以比亞迪股票價格為研究對象，基于GARCH模型族對其進行統計建模，通過分析其波動情況來考察其波動性風險狀況。結果顯示：

比亞迪股票價格時間序列的波動非常頻繁，很不穩定，而其一階差分序列的殘差服從t分布且能用EGARCH（1，1）模型進行較好的擬合，說明該股票價格的分布具有顯著的異方差性。同時，由于一階差分序列的峰度大于標準正態分布的峰度，因此原序列具有“尖峰厚尾”的現象。J-B統計量值為99.28478，對應的P值為0，說明應該拒絕一階差分序列服從正態分布的原假設。同時，也說明該股票的價格具有很強的波動集群性和杠桿效應，其價格波動在部分時刻與往期股票價格的漲跌具有顯著的相關性，并且往期股票價格的漲與跌對當前以及未來股價的影響是不對稱的，即投資者對股票價格下跌的反應往往高于相同程度價格上漲的反應，也即價格以及收益率的下跌對該股票價格的影響更大。通過EGARCH模型的系數發現，該只股票的風險與收益是正相關的，符合風險溢出理論。以上對比亞迪股票價格波動性的實證研究，為判斷該股票價格的基礎性質、一般波動規律和投資者偏好，提供了一定的參考價值。

參考文獻：

[1]羅永亮.上海股票市場波動性的研究[D].中山大學，2013.

[2]張同功.我國股票市場系統性風險的國際比較與預測.2016.

[3]Vicent Arago-Manzana， “Teorías sobre cobertura con contratos de futuro”？Cuadernos de Economia ， 2017 October.

[4]唐小鳳.ARCH模型在金融市場中的應用[J].數學研究，2017（10）.

[5]嚴定琪，李育鋒.基于GARCH族模型的滬深300指數波動率預測[J].蘭州交通大學學報，2018（22）.

[6]李存行，張敏，陳偉.自回歸條件異方差模型在我國滬市的應用研究[J].數學的實踐與認識，2016（4）.

[7]李亞靜，朱宏泉，彭育威.基于GARCH模型族的中國股市波動性預測[J].數學的實踐與認識，2015.

作者簡介：王晟坦途（1994-），男，江蘇溧陽人，碩士，研究方向為數量經濟學。