基于熵權-FCM的區域管制席亞健康狀態劃分方法

岳仁田，韓 娜，趙嶷飛

(中國民航大學空中交通管理學院，天津 300300)

近幾年隨著空中交通流量的迅猛增長，民航空域接近飽和，管制員工作趨向超負荷狀態，此時管制員發出的指令容易發生錯忘漏現象，管制工作趨于亞健康狀態。而如何對區域管制席亞健康狀態進行合理劃分將是管制運行系統采取合理管控措施的基礎，對緩解管制員工作負荷和疲勞具有重要的意義。目前針對管制員工作負荷和空管安全運行評估方面已有大量的研究，如靳慧斌等[1]基于視覺觀察和語音通話，提出對應的交互指標對管制員工作負荷進行實時測量;高偉等[2]基于加權灰色關聯度方法，建立了管制員工作負荷影響因素評價模型；溫瑞英等[3]基于空中交通的復雜性，提出了嶺回歸-BP神經網絡模型用來預測管制員的工作負荷；趙嶷飛等[4]結合集對分析方法和物元可拓理論，構建了管制運行風險評價模型對某管制單位運行風險進行評價；廖勇等[5]建立了一種基于Bayes分析的空管安全概率評估方法；Jacek[6]運用模糊風險矩陣評估了空中交通事故發生的可能性；Li等[7]利用事故樹方法分析了ATC自動化系統升級過渡過程中的安全風險；張兆寧等[8]建立了熵流模型，利用系統熵變分析了進近管制系統風險性變化的趨勢；王潔寧等[9]利用系統性事故理論分析方法(STPA)，識別了管制員潛在的不安全行為，并建立了不安全行為約束的形式化表達式；Micha等[10]依據人為因素分析和分類系統(HFACS),提出了STAMP-HFACS圖，減少了STAMP的誤分類率。另外，在空管運行亞健康理論方面，岳仁田等[11]建立了可接受空中交通流不均衡度(AATFID)模型，首次從管制員工作負荷角度描述了管制運行系統亞健康狀態[12]，并從人員、設備、環境、管理和運行5個角度構建了空管運行亞健康狀態評估指標體系，建立了空管運行亞健康狀態灰色層次評價模型[13]。

由于區域管制席亞健康狀態的特性具有模糊性和不確定性，可能會發展為健康狀態或故障狀態。而聚類分析作為一種無監督學習算法，能夠在沒有任何先驗知識的情況下實現數據集的特征劃分。聚類算法在分類的過程中，不必事先給出一個分類的標準，能夠從樣本數據出發，自動進行分類。模糊C均值聚類(FCM)算法[14]使用模糊邏輯和模糊集合論的概念，提出一種不需硬性地將對象指派到一個簇中的聚類算法，為每個對象和每個簇賦予一個隸屬度，指明該對象屬于該簇的程度。但考慮到空中交通流具有時空不均衡性質[11]，若將各亞健康狀態評價指標同等對待，區域管制席亞健康狀態劃分結果會存在較大的誤差。因此，為了提高區域管制席亞健康狀態劃分的準確性，本文基于管制員工作負荷選取5項評價指標，針對各評價指標對區域管制席亞健康狀態的影響程度不同，先利用熵權法對區域管制席亞健康狀態評價指標進行賦權，然后根據區域管制員在北京部分扇區的練習數據，運用基于熵權的模糊C均值聚類(EW-FCM)算法對其進行聚類劃分，最后通過實例仿真驗證了本文提出的基于熵權-FCM的區域管制席亞健康狀態劃分方法的有效性。

1 FCM算法原理

模糊C均值聚類(FCM)算法是一種實行模糊偽劃分的軟聚類方法，通過迭代使樣本距離模糊聚類中心的距離加權和最小。若一個數據集為X={x1，x2,…,xn},每個樣本xi有m個評價指標，即xi={xi1,xi2,…,xim}，樣本集X的一個子集為模糊簇集V1,V2,…,Vc。FCM算法的目標函數為

(1)

(dij)2=‖xj-vi‖2=(xj-vi)T(xj-vi)

(2)

式中：vi為第i個聚類中心，其計算公式見下文。

FCM算法的具體步驟如下：

(1) 選擇聚類數目c，設置模糊指數q、迭代終止閾值ε和最大迭代次數T，隨機初始化隸屬度uij。

(2) 計算模糊聚類中心，其具體計算公式為

(3)

(3) 更新模糊偽劃分，計算聚類隸屬度矩陣，其計算公式為

(4)

(4) 重復計算每個聚類中心和隸屬度矩陣，直至劃分結果達到穩定狀態(終止迭代條件：“如果誤差的變化低于指定的閾值”或“如果所有的隸屬度變化的絕對值都低于指定的閾值”)。

2 基于EW-FCM的區域管制席亞健康狀態劃分方法

2.1 EW-FCM算法

熵是度量系統無序程度的測度，熵值越大，系統的無序程度越高，提供的信息就越少[15]。每個評價指標權重的熵值體現了該指標在區域管制席亞健康狀態劃分中提供有用信息的多少，反映出各評價指標的相對重要性。故本文計算亞健康狀態評價指標權重的步驟如下：

(1) 構建數據矩陣X。若有m組管制運行數據，每組數據有n個亞健康狀態評價指標，則構建數據矩陣X：

X=(xij)m×n(i=1,2,…,m;j=1,2,…,n)

(5)

(2) 對數據矩陣X進行歸一化處理。為了解決各亞健康狀態評價指標量綱不同的問題，需對數據矩陣X進行歸一化處理，其計算公式為

(6)

(3) 計算各亞健康狀態評價指標的熵值。各亞健康狀態評價指標j熵值的計算公式為

(7)

(4) 計算各亞健康狀態評價指標的熵差異系數。亞健康狀態評價指標j的熵差異系數計算公式為

dj=1-Ej(j=1,2,…,n)

(8)

(5) 計算各亞健康狀態評價指標的權重。用熵測度來表示第j個亞健康狀態評價指標的權重系數，其計算公式為

(9)

根據上述熵權法步驟對各亞健康狀態評價指標賦權后，利用計算的誤差平方和來確定每組樣本數據與聚類中心間距的最小值。改進的模糊C均值聚類(EW-FCM)算法的目標函數為

(10)

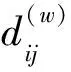
(11)

式中：w={w1,w2,…,wt},wk∈[0,1],為亞健康狀態評價指標的權值；t為亞健康狀態評價指標的個數，取t=5。

2.2 EW-FCM算法的實現步驟

EW-FCM算法的實現步驟如下：

(1) 依據熵權法計算出各亞健康狀態評價指標的權重W={w1,w2,w3,w4,w5}，將其代入公式(11)計算加權歐氏距離。

(2) 根據區域管制席的練習數據特征，設置模糊指數q、迭代終止閾值ε和最大迭代次數T。

(5) 當收斂精度達到ε，算法終止；否則，返回步驟(3)，繼續迭代計算V、U。

2.3 改進前后的FCM算法評價

為了評估模糊聚類算法的有效性，選擇劃分系數PC[16]、劃分熵系數PE[16]、改進的劃分系數MPC[16]、目標函數值和迭代次數對改進前后的FCM算法的聚類效果進行對比分析。

(1) 劃分系數PC的計算公式如下：

(12)

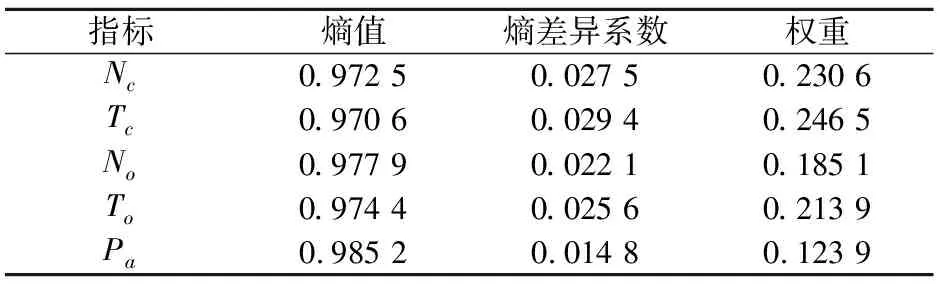
式中：c為聚類中心的個數；n為模糊聚類的樣本數量。當1

(2) 劃分熵系數PE的計算公式如下：

(13)

PE的取值范圍為[0,logc]，若結果越接近0，聚類劃分越清晰；若結果越接近logc，聚類劃分越模糊。

(3) 采用改進的劃分系數MPC對PC和PE的單調傾向進行了優化，其計算公式如下：

(14)

(4) 目標函數值和迭代次數:FCM算法的目標函數是某樣本的隸屬度與該樣本到各亞健康狀態聚類中心距離的乘積，可以用來衡量聚類中心是否能準確表示各亞健康狀態中心的指標,若聚類算法的目標函數值越小，則聚類中心更能代表各亞健康狀態的中心。迭代次數是聚類算法計算樣本數據隸屬度和亞健康狀態聚類中心的運行次數，迭代次數越少，表明聚類算法的收斂性越好。

3 實例仿真分析

3.1 數據采集

本文以區域管制員在北京部分扇區的練習數據為樣本數據，樣本數據采集間隔為3 min，共100組，每組樣本數據包括亞健康狀態劃分的5個評價指標[9]，依次為通話次數(Nc,次)、通話時間(Tc,s)、設備操作次數(No,次)、設備操作時間(To,s)、同時監管的飛機峰值架次(Pa,架次)。在樣本數據預處理過程中需依據熵權法計算亞健康狀態評價指標的權重，再利用FCM算法和EW-FCM算法得到區域管制席亞健康狀態劃分結果。而數據的歸一化處理是熵權法必不可少的步驟，其可以提升FCM算法聚類的準確性。因此，本文在對樣本數據預處理過程中，對100組樣本數據進行了標準化處理，再利用熵權法計算區域管制席亞健康狀態評價指標的權重，其計算結果見表1。

表1 基于熵權法的區域管制席亞健康狀態評價指標權重

由表1可知，區域管制席亞健康狀態評價指標的權重向量為W={w1,w2,w3,w4,w5}={0.230 6，0.246 5，0.185 1，0.213 9，0.123 9}，管制員通話的兩項指標反映出的信息量均大于設備操作的兩項指標，而同時監管的飛機峰值架次反映出的信息量最小。這也進一步說明了熵權法在EW-FCM算法中具有良好的適用性。

3.2 改進前后的FCM算法聚類效果對比

根據樣本數據的性質，FCM算法仿真中采用MATLAB默認模糊指數q=2、迭代終止閾值ε=1.0×10-6和最大迭代次數T=100。由于FCM算法聚類的優劣與選取的簇數有關，若選取的聚類簇數量太少，不能反映不同區域管制席亞健康狀態的區別；若選取的聚類簇數量太多，不能表現區域管制席亞健康狀態的聚類效果。因此，根據區域管制席亞健康狀態的特性，按照經驗設置聚類數目c=3。FCM算法和EW-FCM算法的有效性指標計算結果，見表2。

表2 改進前后的FCM算法的有效性指標

注:表中加粗數據值所對應的算法較優。

由表2可知，EW-FCM算法的劃分系數PC、劃分熵系數PE、改進的劃分系數MPC均比FCM算法更優，直接表明EW-FCM算法比傳統FCM算法的聚類效果更為理想。

為了驗證EW-FCM算法的有效性，計算了樣本數據的目標函數值和迭代次數，其計算結果見圖1。

圖1 改進前后的FCM算法目標函數值變化曲線Fig.1 Variation curves of objective function value of FCM algorithm before and after improvement

由圖1可見，在首次迭代時，EW-FCM算法的目標函數值(約為7)遠遠小于FCM算法的目標函數值(約為200)，這是由于使用熵權法對亞健康狀態評價指標賦予了不同的權重，而傳統的FCM算法中每個指標的權重都是1，因此首次迭代計算的目標函數值大大降低，所得的聚類中心能更好地表示區域管制席亞健康狀態的中心，這提升了最終目標函數值和聚類中心的迭代效率；在迭代過程中，兩種聚類算法的目標函數值都在持續減小，但EW-FCM算法達到目標函數最小值的迭代次數(12次)小于FCM算法達到目標函數最小值的迭代次數(18次)；在迭代結束時，EW-FCM算法的目標函數最小值(約為5.2)遠遠小于FCM算法的目標函數最小值(約為155)。改進前后的FCM算法聚類效果對比結果表明：EW-FCM算法相較于FCM算法，在較少的迭代次數下達到了更小的目標函數值，且收斂效率和收斂性能均有所提高。

3.3 結果分析

根據EW-FCM算法的聚類結果，分三組計算區域管制席亞健康狀態評價指標的均值，并統計各類管制練習數據的數量，見表3。

表3 區域管制席亞健康狀態評價指標的均值

注：表中加粗數據值表示明顯大于樣本數據均值。

由表3可以看出：

(1) Ⅰ 類管制數據的各項評價指標均值均小于樣本數據，此類練習數據表示出區域管制工作負荷量較小，管制員能夠很輕松地完成管制任務，此時管制運行席位處于健康狀態。

(2) Ⅱ 類管制數據中前兩項的通話指標均值和同時監管的飛機峰值架次指標均值遠大于樣本數據，設備操作的兩項指標均值小于樣本數據，此時管制員同時監管的飛機峰值架次過多，通話工作負荷較重，發出的指令較多且復雜，將此類管制運行席位標定為通話亞健康狀態。

(3) Ⅲ類管制數據中設備操作的兩項指標均值均大于樣本數據，其他3項評價指標均值約等于樣本數據，此時管制員設備操作負荷較重，相比Ⅱ類的通話亞健康狀態，將此類管制運行席位標定為設備操作亞健康狀態。

通過統計分析，100組練習數據中有35%處于健康狀態，分別有26%和39%處于通話亞健康狀態和設備操作亞健康狀態，樣本數據集中只有1/3的練習數據處于健康狀態，直接表明區域管制練習整體上呈現一種亞健康趨勢，這與北京扇區的航線密集和空域復雜導致的管制工作量劇增有必然的聯系。

文獻[11]將管制運行狀態劃分為健康狀態和亞健康狀態(包含管制運行穩定亞健康狀態和不穩定亞健康狀態)，而在本文中將區域管制席亞健康狀態劃分為健康狀態、通話亞健康狀態和設備操作亞健康狀態，從成因角度劃分了區域管制席亞健康狀態。若區域管制席處于健康狀態時，管制員能高效率地完成管制工作任務，交通服務水平良好，則適宜安排在交通流量高的時段執勤;若區域管制席處于通話亞健康狀態時，管制員同時監管的飛機峰值架次過多，導致其在管制信息收集與決策過程中，不能發出簡潔、準確的指令，指揮能力逐漸下降，則不適宜安排在管制任務繁忙的時段工作；若區域管制席處于設備操作亞健康狀態時，管制員對各種管制設備的操作能力較弱，則可以使用雷達管制模擬機勤加練習，提升設備操作的熟練程度。

根據成因角度劃分區域管制席亞健康狀態，可以及時地掌握管制運行的健康程度。若區域管制席長期處于某種亞健康狀態，會造成管制員持續超負荷工作，出現精神疲勞和心理疲勞等現象，則極有可能發生指揮失誤、危險接近等不安全事件。所以，應當及早對區域管制席亞健康狀態進行識別，并采取合理的控制和誘導措施，保障管制運行工作的安全、有效運行。

4 結論與建議

通過區域管制席亞健康狀態劃分可以全面地掌握ATC的運行情況，有助于管制運行潛在性風險的預判，是及時采取交通管控和誘導措施的前提。本文利用熵權法對區域管制席亞健康狀態評價指標進行賦權，將傳統的歐氏距離改進為帶權重的歐氏距離，并基于北京部分扇區的練習數據，得到5項亞健康狀態評價指標，其中關于陸空通話的兩項指標對區域管制席亞健康狀態劃分的影響最大。通過實例仿真結果表明：本文的EW-FCM算法相較傳統的FCM算法，能對區域管制席亞健康狀態進行合理有效的劃分，且收斂性能較好。未來研究可加入管制任務中的思考工作負荷量，對區域管制席亞健康狀態進行深入分析。此外，研究區域管制席在亞健康狀態下的交通流時空分布特性，對管制空域的扇區容量設定具有一定的參考意義。