大深度潛航器水下空間運動建模與仿真

喬 冰，劉 鑫，袁 龍

（1.中國船舶重工集團有限公司第七一〇研究所，湖北 宜昌 443003；2.中國人民解放軍32023部隊，遼寧 大連 116000；3.中國人民解放軍32033部隊，海南 海口 571100）

0 引言

自主式水下無人潛航器（AUV）是在無人操控的情況下自主完成復雜海洋環境作業的水下機器人，廣泛應用于海洋觀測和海洋作業領域[1-2]。對于大深度作業的潛航器，其續航能力、空間運動能力、航行穩定性等是其水下深海作業的基礎。通過數學仿真手段，分析大深度潛航器水下空間運動狀態，對潛航器總體設計和參數優化具有深遠的指導意義。

本文研究的大深度潛航器為深海搜索探測型AUV，其通過釋放浮筒裝置產生負浮力，并結合安裝在頭部附近的弧形翼板提供側向力和力矩，實現潛航器的無動力螺旋下潛。當潛航器到達預定水深時，將弧形翼板和下潛壓載同時釋放，此時潛航器穩定過渡至預定水深航行；當潛航器上浮時，通過釋放上浮壓載產生正浮力實現定角爬升；當接近水平面時，釋放平衡壓載實現穩定過渡至水面。其水下空間運動過程如圖1所示。本文對潛航器在大攻角條件下進行運動建模與仿真，分析其在弧形翼板作用下的螺旋下潛以及拋載調節質浮心距實現下潛、上浮的運動特性，并實現各運動過程之間進行切換，給出潛航器水下空間運動全過程仿真結果。

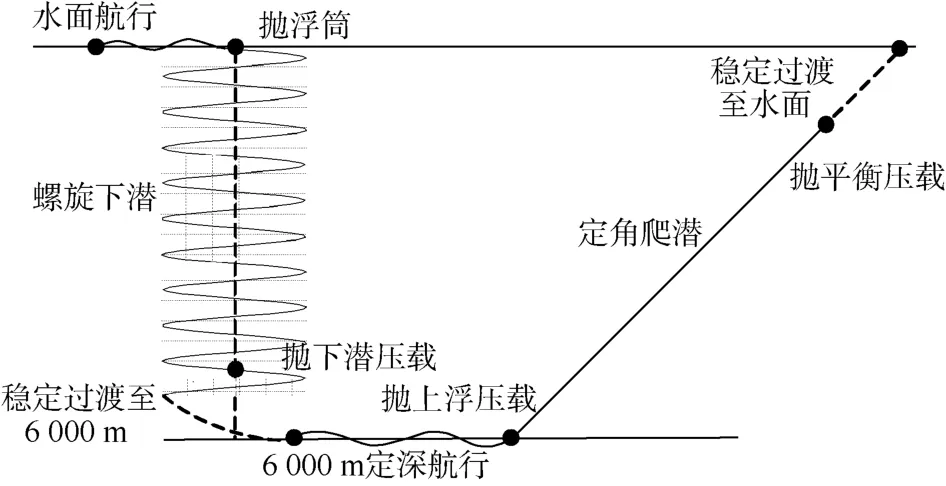
圖1 潛航器水下空間運動方案Fig.1 Underwater space motion scheme of vehicle

1 潛航器外形

潛航器外形為回轉體，為了實現潛航器無動力螺旋下潛運動，在潛航器首部下潛壓載下方加裝弧形翼板。弧形翼板的安裝位置和局部細節如圖2所示。

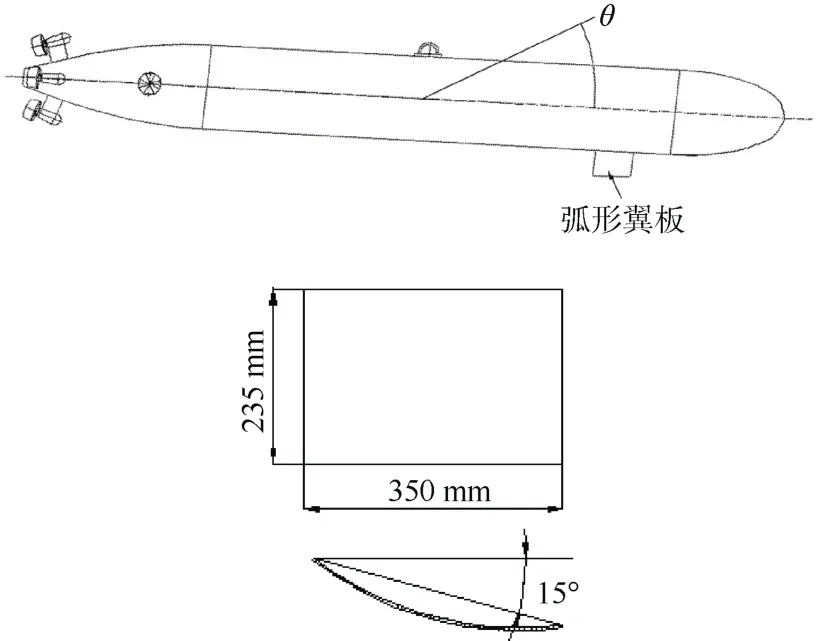
圖2 弧形翼板安裝位置及細節圖Fig.2 Installation position and detail diagram of arc wing-plate

弧形翼板隨下潛壓載一同安裝釋放，主要功能是實現潛航器的無動力螺旋下潛。當潛航器到達預定水深時，將弧形翼板和下潛壓載同時拋掉，此時潛航器在預定水深達到平衡，開始工作。

2 潛航器空間運動建模

建立潛航器水下空間運動模型是研究其空間運動的基礎。根據大深度潛航器空間運動特點，建立描述其空間運動的數學模型，并將數學模型進行二次建模轉換，建立潛航器空間運動仿真模型，用于大深度潛航器水下空間運動仿真研究。

2.1 建模流程

為確保建立潛航器空間運動模型的正確性和適用性，如圖3所示，建模以下流程。

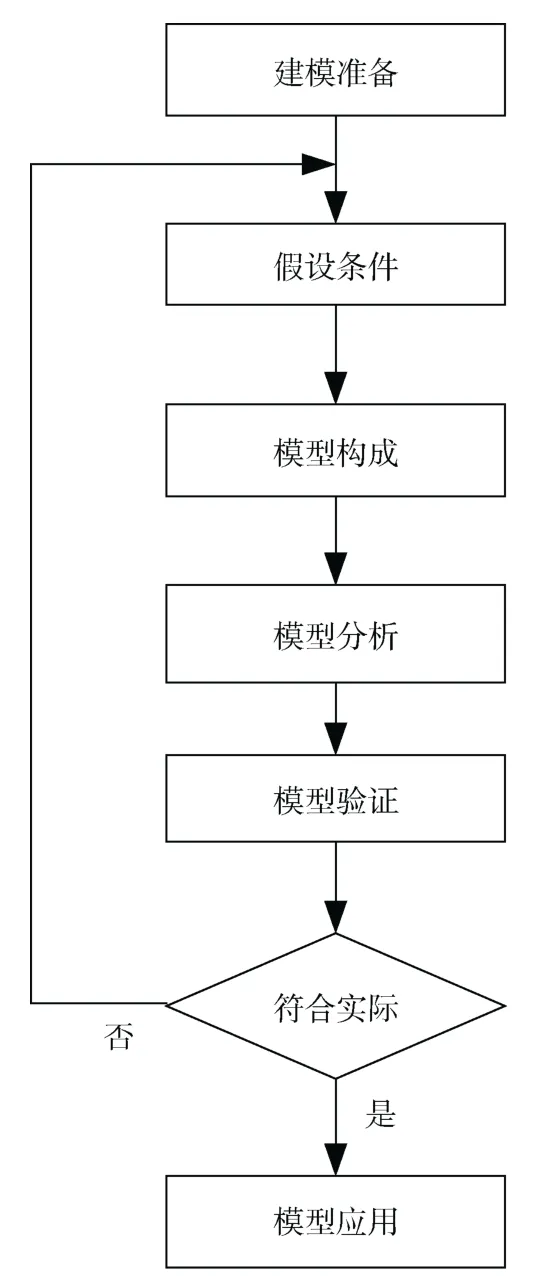
圖3 潛航器空間運動建模流程Fig.3 Modeling flow of vehicle’s space motion

1）建模準備。

了解仿真需求和潛航器的自身特點，掌握其空間運動特點，為仿真建模奠定基礎。

2）假設條件。

分析潛航器建模的主要作用因素，包括空間運動規律、流體參數和衡重參數等作用因素，并假設研究對象為水下全沾濕狀態下進行模型的搭建。

3）模型構成。

根據建模的假設條件和建模原理，引入描述潛航器空間運動規律運動學模型和動力學模型，選取合適的建模坐標系（詳見章節2.2），建立在相應坐標系下的潛航器空間運動數學模型。

4）模型分析。

基于上述準備，完成對潛航器空間運動微分方程組的理論推導，通過數值求解得到初步的空間運動軌跡，并對結果進行數學分析。

5）模型驗證。

對所建模型在典型工況下進行數學仿真計算，并分析仿真結果是否滿足要求，分析其運動規律與設定結果是否接近或相符。

6）模型應用。

在模型驗證正確的基礎上，根據仿真的用途和建模的目的將潛航器數學模型轉化為適用于仿真分析的仿真模型，應用于仿真分析研究。

2.2 建模坐標系

選取合適的建模坐標系是建立潛航器空間運動數學模型的前提。本文采用大地坐標系o0x0y0z0和體坐標系oxyz為基礎建立潛航器空間運動數學模型，現給出各個坐標系的定義及相互轉換關系。

1）大地坐標系o0x0y0z0。

大地坐標系相對于地面靜止不動。其原點o0選在地面某處；o0x0軸在水平面內指向任意方向；o0y0軸鉛直向上；o0z0軸垂直于o0x0和o0y0軸，其方向使該坐標系成為右手坐標系。潛航器相對大地坐標系的運動就是其相對地面的運動。

2）體坐標系oxyz。

體坐標系也稱運動坐標系，體坐標系各坐標軸與潛航器固連（相對于潛航器靜止不動）。體坐標系的原點o選在潛航器的浮心處；ox軸沿潛航器縱軸并指向前方；oy軸位于潛航器的縱向對稱面內，與ox軸垂直并指向上方；oz軸垂直于ox和oy軸，其方向使該坐標系成為右手坐標系（從潛航器尾部向前看oz軸指向右側）。

3）坐標系轉換。

大地坐標系與體坐標系如圖4-5所示。

圖4 大地坐標系示意圖Fig.4 Schematic diagram of geodetic coordinate

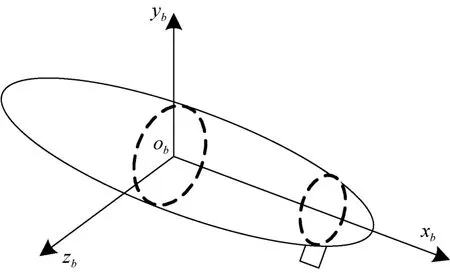
圖5 體坐標系示意圖Fig.5 Schematic diagram of volume coordinate

體坐標系相對與大地坐標系的姿態，利用3個姿態角θ、ψ、φ進行描述，分別為俯仰角、偏航角、橫滾角。從大地坐標系（用o表示）到體坐標系（用b表示）的轉換矩陣為

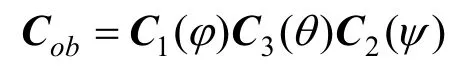
展開表達式有：

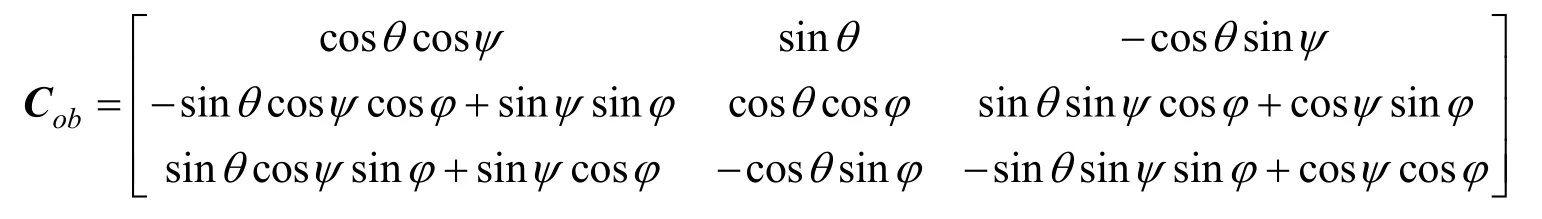
根據矩陣的正交性，體坐標系到大地坐標系的坐標轉換矩陣為

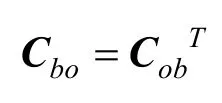
2.3 數學模型

建立潛航器空間運動數學模型時，可視其為剛體，將流體動力和其他作用力作為外力。根據上述坐標系及轉換矩陣推導出空間運動方程；根據動力定理和動量矩定理推導出動力學方程[3]；潛航器空間運動數學模型由運動學模型和動力學模型組成。

1）運動學方程。

運動學方程由描述潛航器空間運動的航行軌跡方程和轉動運動方程組成，具體數學模型描述為

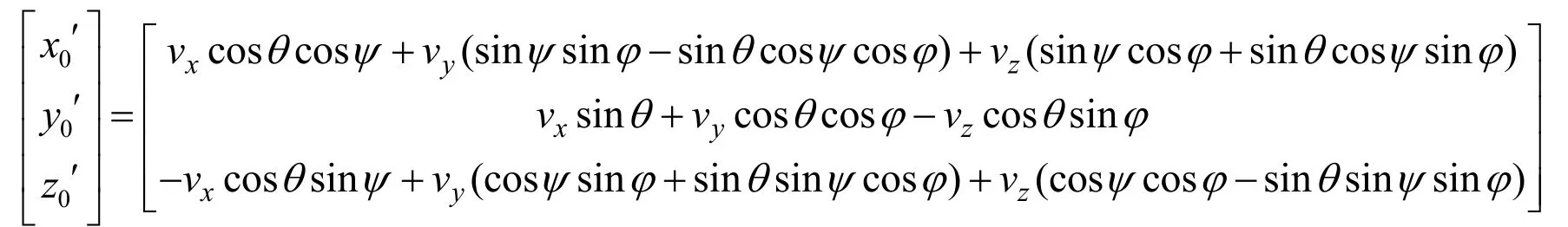
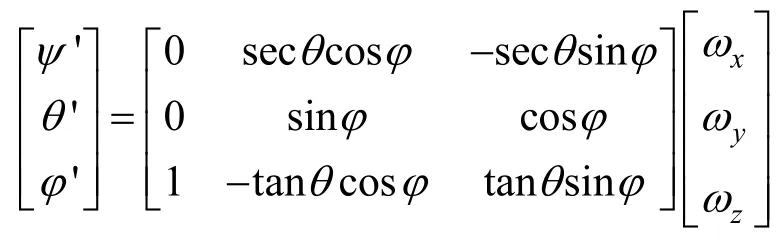
式中：x0、y0、z0為潛航器相對于大地坐標系的位 置 ；vx、vy、vz為 潛航器浮心在體坐標系中相對各坐標軸的速度分量；ωx、ωy、ωz為潛航器旋轉角速度在體坐標系中相對各坐標軸的角速度分量。

2）動力學方程。

根據空間剛體的動量定理和動量矩定理，在大地坐標系中有：

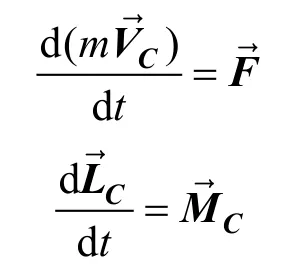
將上述向量式展開，并忽略無窮小項，得到動力學方程組：

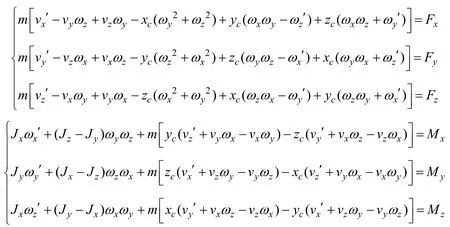
式中：Fx、Fy、Fz和Mx、My、Mz分別為作用于水下潛航器各坐標軸上的外力和力矩之和；xc、yc、zc為潛航器的質浮心距；Jx、Jy、Jz為潛航器坐標系下相對各坐標軸的轉動慣量；m為潛航器的質量。

3）流體動力分析。

當潛航器在水中航行時，流體在潛航器外形表面流動，潛航器與流體相互作用便發生在它們相互作用的表面[4]，因此潛航器的外形設計決定了其流體動力學性能。文中研究的潛航器通過首部設計的弧形翼板實現螺旋下潛運動，采用數值水洞仿真試驗方法[5]計算潛航器運動過程的流體動力系數，并施加在動力學方程中進行空間運動解算。

由于潛航器在螺旋下潛的過程中，會產生較大的攻角和側滑角，因此流體動力表現出明顯的非線性[6]。在進行流體動力參數擬合過程中，關于攻角的流體參數，采用多項式形式表達，充分考慮了參數的非線性問題。其中，升力系數和俯仰力矩系數擬合結果為

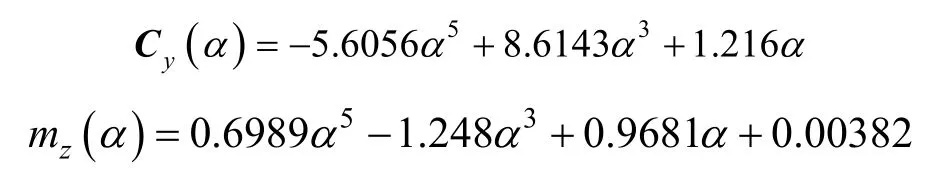
2.4 仿真模型

建立潛航器空間運動仿真模型就是將上述數學模型通過仿真軟件轉化為適用于計算機仿真分析的過程。根據潛航器空間運動特點，空間運動描述要求在大攻角條件下進行建模仿真。基于上述數學模型的推導和建模流程，利用 MATLAB/Simulink模塊化建模方式實現潛航器的空間運動仿真模型的搭建[7-8]。仿真模型采用的模塊化設計，方便模塊的移植和編寫，并且易于對特定參數進行修改。

3 潛航器空間運動仿真

根據研究對象空間運動的特點，潛航器在進行大深度水下運動過程中包含螺旋下潛段、拋載過渡段、定角爬升段、穩定至水面段4種運動過程。其運動過程是在大攻角狀態下進行的，并在各個運動階段之間進行切換，參數變化較復雜，仿真難度較大。本文通過計算仿真輔助手段，對潛航器空間運動進行仿真分析，給出潛航器水下空間運動全過程運動仿真。

3.1 仿真設置

潛航器水下空間全過程運動仿真參數設置如表1所示。

表1 全過程運動仿真設置Table 1 Motion simulation settings of whole process

3.2 仿真曲線

為了便于觀測潛航器水下運動全過程，仿真設計將各個運動階段的仿真時間較實際工作時間縮短。其中，螺旋下潛段的仿真時間為300 s；仿真進行到300 s時，進行拋載動作；穩定過渡至400 s時，進行定角爬升；爬升至900 s時，進行拋載過渡仿真；總仿真時長為1 200 s。潛航器水下空間運動仿真結果如圖6-9所示。

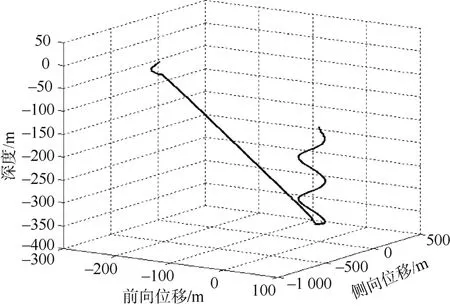
圖6 航行軌跡曲線Fig.6 Navigation trajectory curve

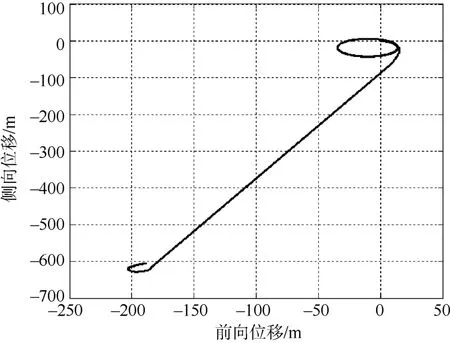
圖7 螺旋下潛回轉直徑Fig.7 Rotating diameter of spiral dive

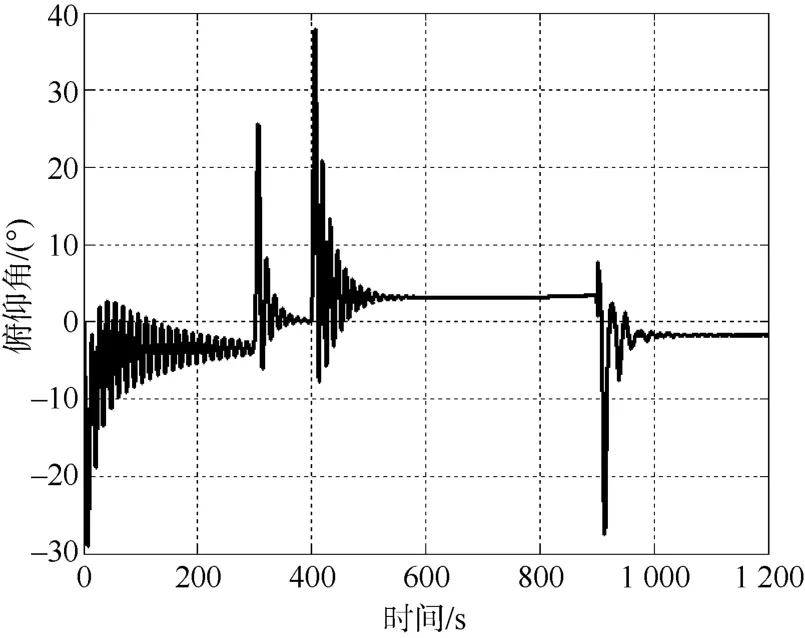
圖8 俯仰角曲線Fig.8 Curve of pitch angle

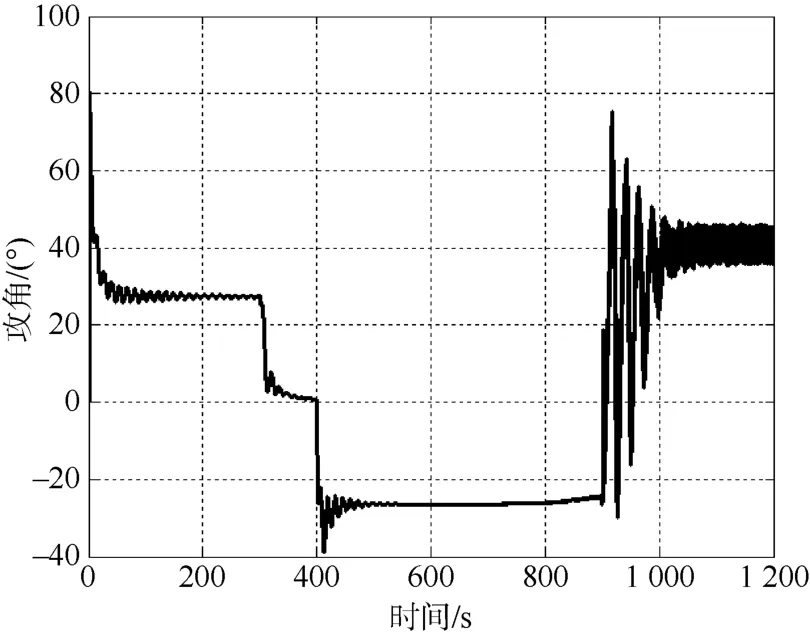
圖9 攻角曲線Fig.9 Curve of attack angle

3.3 結果分析

由上述仿真曲線可知：潛航器在螺旋下潛段（0～300 s）、拋載穩定至水下 6 000 m 段（300～400 s），定角爬升段（400～900 s）的運動狀態均符合預期設想，滿足設計需要；通過運動建模與仿真分析手段有效驗證了潛航器弧形翼板總體設計的可行性和水下空間運動能力。

4 結束語

本文對大深度潛航器的空間運動模型和運動仿真展開了分析和研究。針對潛航器空間運動特點，建立符合其空間運動規律的數學模型和仿真模型；以仿真模型為基礎，通過數學仿真方法分析了潛航器在螺旋下潛、拋載過渡、定角爬升、穩定至水面運動的全過程運動狀態。仿真結果表明：本文所研究的潛航器采用弧形翼板設計可實現螺旋下潛功能，且航行穩定；通過拋載實現潛航體質浮心距的調節，滿足了潛航器在上浮過程定角爬升的要求。

通過對大深度作業下潛航器的建模與空間運動仿真研究，可為設計人員在潛航器弧形翼板總體方案設計及運動參數優化方面提供有效的考核驗證手段，有效指導設計人員評估潛航器的空間運動能力，提前釋放設計風險。