新型猶豫不確定Z-Numbers熵及其多準則群決策分析

鄒 斌

(安徽廣播電視大學 文法與教育學院，安徽 合肥 230022)

為處理模糊信息，Zadeh[1]提出了模糊集理論。在考慮決策問題[2]、模式識別[3]以及模糊推理時[4]，模糊集都是非常有用的工具。然而單憑模糊集中的隸屬度無法精確的描述信息。在解決非隸屬度的不確定性問題上，Atanassov[5]介紹了直覺模糊集，并應用到多準則決策問題中[6]。猶豫模糊集作為傳統模糊集的拓展，這個概念首次被Torra和Narukawa提出[7]。允許元素的隸屬度是幾個可能值的集合，但這些經典模糊集提出的決策信息的可靠性存在一定的局限性[8]。因此，Zadeh提出了一種新的模糊集理論Z-Numbers。Z-Numbers是一個有序的模糊數對，Z=(A,B)是由兩個簡單的結構組成，即約束A和可靠性B。

考慮到Z-Numbers的廣泛適用性及語言模型的有效性，本文討論Z-Numbers的一個特殊分支猶豫不確定語言型Z-Numbers。使用一個區間語言值來描述模糊限制比使用單一的語言值更加合適，因為在現實中由決策者提供的語言限制也就是Z-Numbers的第一部分，決策者通常會在幾種可能的語言值之間波動。

因而一些連續或離散的語言術語可用來描述這種猶豫性，HULZNs有效地展現這種不完全信息，更充分地表示決策信息。在找到能夠完整有效的表示語言信息的模糊數對還無法據此作出最終的決策，本文給出了一種新的語言尺度函數用于度量HULZNs。

文獻[9]把交叉熵應用于區間二型模糊集上，為改進距離相似度公式的缺陷提出了對稱交叉熵。本文針對猶豫不確定語言型Z-Numbers，提出猶豫不確定語言型Z-Numbers的熵。在處理多準則群決策問題[10]時，首先，從文獻[11]關于Z-Number的公理化定義出發，構造一種語言尺度函數；其次，在語言尺度函數基礎上，構造猶豫不確定語言型Z-Numbers的熵，建立決策者權重與準則權重的模型，通過排序公式得出最優方案；最后，通過一個算例與文獻[12]作比較，說明該決策步驟的有效性和可行性。

1 基本概念

這部分內容主要介紹語言型集合，不確定語言變量，語言尺度函數及其性質，猶豫不確定語言型Z-Numbers的概念及運算。

1.1 語言型集合[12]

1.2 不確定語言變量[12]

1.3 語言尺度函數

本節將介紹兩種量化語言的尺度函數。尺度函數能夠直觀有效地將語言轉化為確定的數值，是運用模型作出決策的基礎。

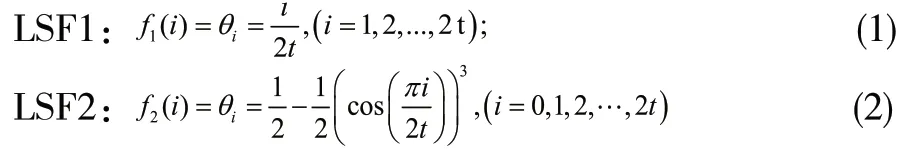
例：令

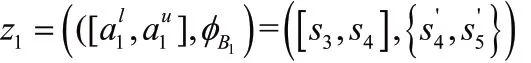
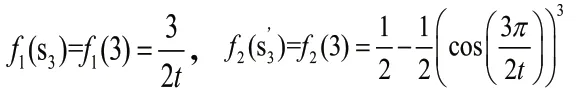
注：為合理精確地表示HULZNs,本文中LSF1是集合Az(x)的尺度函數，LSF2是集合Bz(x)的尺度函數。

語言尺度函數LSF1、LSF2滿足以下3個性質：

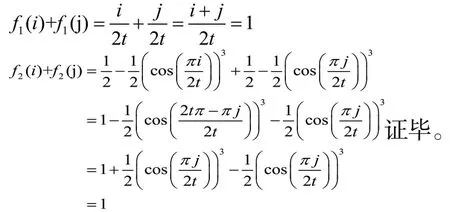
1.4 猶豫不確定語言型Z-Numbers

1.4.1 定義[12]Z-Number 是有序的模糊數對，記為。其中是對不確定變量X的限制，是對的可靠性的度量。

1.4.2 定義[12]設X是一個論域，

1.4.3 定義[12]設任意兩個

1)加法算子

2)數乘算子

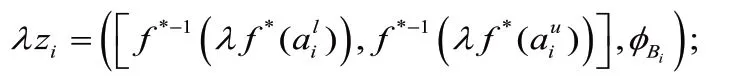
3)冪算子

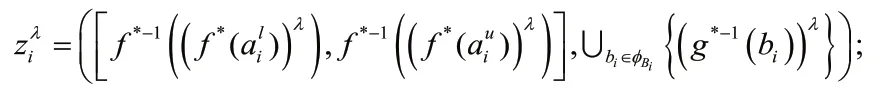
4)否定算子

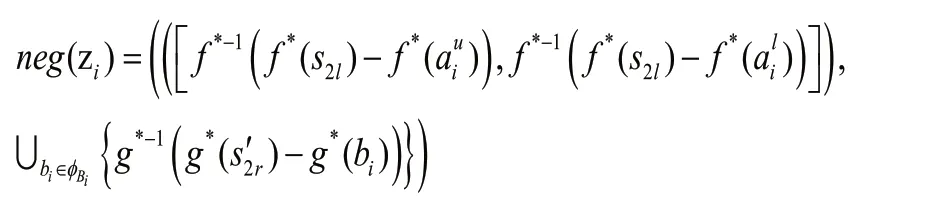
2 猶豫不確定語言型Z-numbers (HULZNs)的交叉熵與熵

在HULZN的模糊環境中度量兩個模糊數之間的關系在實際應用中具有十分重要的作用。本文提出的HULZNs的相對交叉熵及熵，主要從其模糊性、猶豫性來度量兩個HULZNs之間的不確定信息，并用于求權重以及相關的決策排序。

2.1 HULZNs的交叉熵

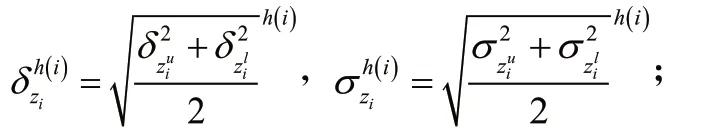
2.1.2 定義設任意兩個猶豫不確定Z-numberzi，zi。相對于zj的相對交叉熵公式定義如下：

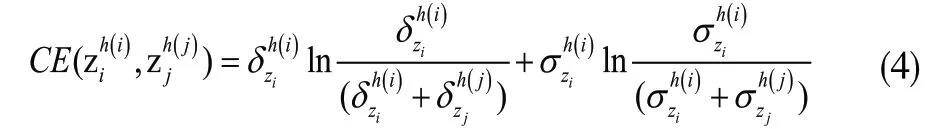
在討論具體問題時，相對交叉熵公式不具備對稱性。因此，定義相應完整的交叉熵公式。

2.1.3 定義設任意兩個猶豫不確定Z-numberzi，zi；與zj的交叉熵公式定義如下：

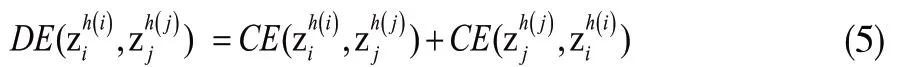
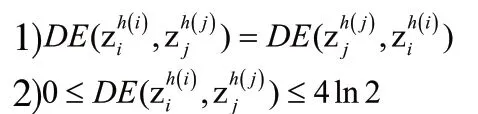
2.2 HULZNs的熵

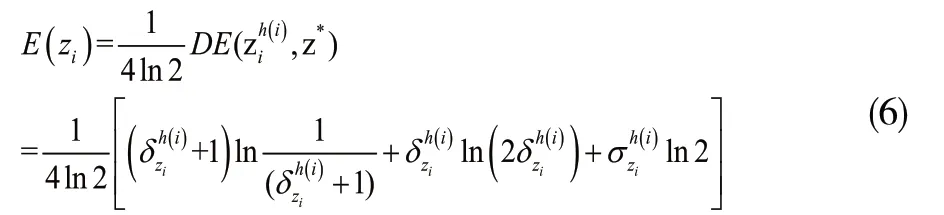
1)E(zi)=0當且僅當，zi是一個確定集，其中=0；

2)對任意的HULZNzi，；

證明：如果zi是一個確定集，即zi=z*，=1，=0得證畢。

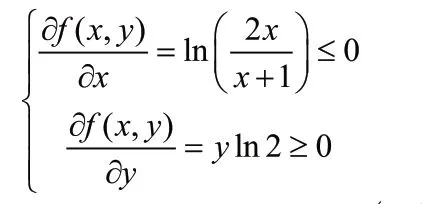
3 猶豫不確定語言型Z-numbers的多準則群決策方法

本節主要構造用于確定決策者權重和準則權重的優化模型，通過猶豫不確定語言型Z-numbers的交叉熵和熵來創建一種新型的多準則群決策方法。

猶豫不確定語言型Z-numbers的多準則群決策問題是由一組可供選擇的方案構成。準則的權重滿足；

3.1 構建最優模型確定權重

決策者權重和準則權重是未知待定或是部分未知的。由此，構建兩個基于HULZNs熵度量的最優模型，用于計算決策者權重和準則權重。依據不同個體決策矩陣間的距離來計算決策者權重，決策個體權重越大表明其在決策過程中越重要。具體模型如下：

下面給出確定準則權重的最優模型：

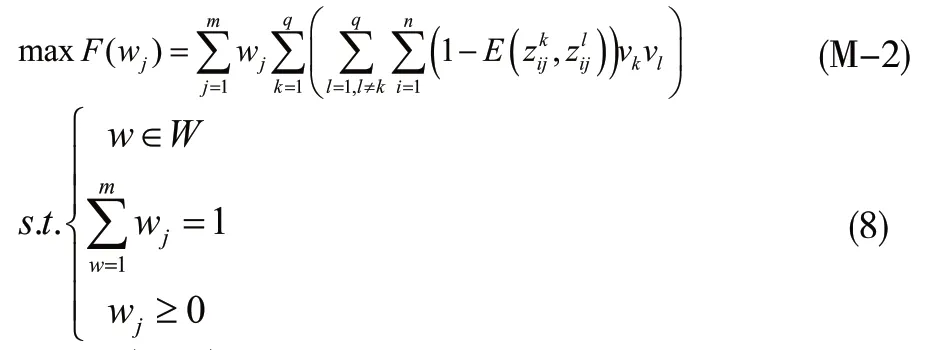
3.2 決策步驟

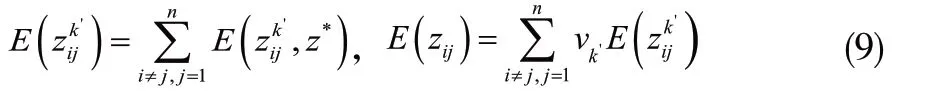
其中z*是一個確定集。

步驟5 計算各方案的擬合度得分并排序，得分最高即為最優方案

4 實例分析

某企業計劃購進一種綜合性能最優的企業資源規劃系統，其選擇標準分為四類：系統功能(c1)，供應商能力和信譽(c2)，系統合適度(c3)，系統靈活性(c4)。經3個專家的初步篩選，現有4個可供選擇的企業資源規劃系統。在激烈討論后，給出關于決策者和標準的部分權重信息：

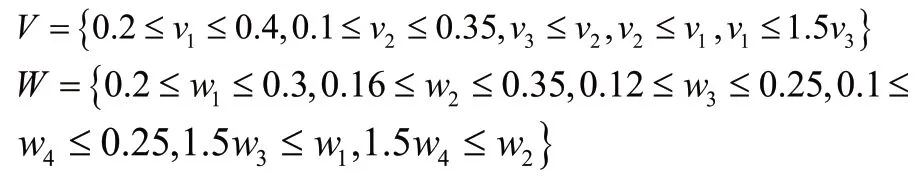
HULZNs的評估值見表1、2和3。

步驟2 根據公式(5)得到交叉熵矩陣：

表1 專家d1的性化推薦矩陣

表2 專家d2的性化推薦矩陣

表3 專家d3的性化推薦矩陣

步驟3 根據上文給出的最優化模型，得到決策者權重與標準權重分別是 ，

步驟4 結合求得的決策者權重和公式(6)，綜合熵決策矩陣表示為：

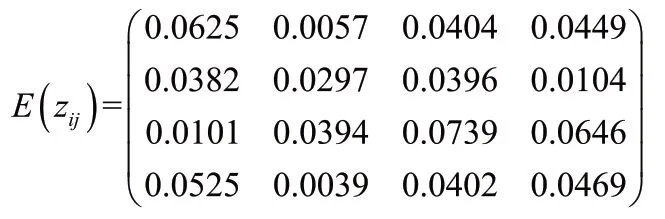
5 結論

本文給出了新的語言尺度函數及猶豫模糊不確定語言型Z-Numbers的熵，并提出基于語言尺度函數的距離公式，其簡練且具有高分辨度，一定程度上解決了計算的復雜性和誤差。 在最終的排序結果，本文得出的最優方案同文獻[12]相同，但其他方案的排序略有不同。說明了本文決策步驟的可行性與有效性。