水聲傳感器網(wǎng)絡(luò)信號到達時間差目標(biāo)定位的最小二乘法估計性能

王領(lǐng)，申曉紅，康玉柱，花飛，王海燕,2

(1.西北工業(yè)大學(xué) 航海學(xué)院，陜西 西安 710072；2.陜西科技大學(xué) 電子信息與人工智能學(xué)院，陜西 西安 710021)

0 引言

在海洋環(huán)境監(jiān)測中，分布式水聲傳感器網(wǎng)絡(luò)是一種方便靈活的監(jiān)測手段，目標(biāo)定位是海洋環(huán)境監(jiān)測的一個基本功能。國內(nèi)外學(xué)者對基于多傳感器節(jié)點的協(xié)同目標(biāo)定位方法已開展了廣泛研究[1-8]。常用協(xié)同目標(biāo)定位方法的基本思想是：假設(shè)傳感器網(wǎng)絡(luò)各節(jié)點位置準(zhǔn)確已知，每個節(jié)點獲取觀測值后，依據(jù)一定的定位算法提取其相關(guān)信息并傳輸至中心節(jié)點，中心節(jié)點依據(jù)獲得的信息對聲源位置進行估計[1-8]。其中，常用的基于測距的目標(biāo)定位算法有基于信號到達時間算法、基于信號到達時間差(TDOA)算法、基于信號到達角度算法、基于到達頻差算法、基于信號到達強度算法，以及以上算法的組合。由于基于TDOA的目標(biāo)定位算法具有硬件要求低(每個節(jié)點僅需要有一個接收通道)、計算復(fù)雜度低、定位精度高等優(yōu)點，是基于傳感器網(wǎng)絡(luò)節(jié)點對目標(biāo)被動定位的首選算法[9-12]。在TDOA目標(biāo)定位算法中，以Chan算法[13]、泰勒級數(shù)展開算法[14]和近似最大似然估計算法[15]的精度最高。特別是Chan算法采用基于兩步加權(quán)最小二乘(WLS)算法給出了定位算法的解析解，并從理論和仿真兩個角度證明當(dāng)噪聲較小且服從高斯分布時，其均方誤差能達到克拉美羅下界(CRLB)[13]。由于性能優(yōu)越，Chan算法得到了廣泛應(yīng)用。

目前研究的協(xié)同目標(biāo)定位算法大多是針對陸地電磁波傳感器節(jié)點的[1-13]。由于陸地傳感器節(jié)點可借助于衛(wèi)星使節(jié)點本身的位置誤差較小，這些算法均假設(shè)傳感器節(jié)點的位置準(zhǔn)確已知，僅考慮對目標(biāo)到達時間差的測量誤差。水聲傳感器網(wǎng)絡(luò)是以水聲為通信介質(zhì)，以海洋環(huán)境監(jiān)測為目的，工作于水下，無法用衛(wèi)星進行自定位，通常采用基于距離的傳感器節(jié)點自定位。由于水聲的非直線及長時延多徑傳播，使得水聲節(jié)點的自定位誤差遠(yuǎn)比基于衛(wèi)星的自定位誤差大(1個數(shù)量級以上)。此外，由于水中的浮標(biāo)或潛標(biāo)會隨洋流飄動，在水聲傳感器網(wǎng)絡(luò)對目標(biāo)定位的算法中不能忽略節(jié)點的自定位誤差，在這種情況下研究如何提高水聲網(wǎng)絡(luò)傳感器節(jié)點對目標(biāo)的協(xié)同定位精度，是十分迫切的。

本文針對水聲傳感器網(wǎng)絡(luò)目標(biāo)定位中節(jié)點位置誤差和測距誤差同時存在條件下的目標(biāo)定位性能問題，建立雙誤差條件下的TDOA目標(biāo)定位模型；提出一種基于加權(quán)整體最小二乘(WTLS)算法的TDOA目標(biāo)定位算法，將測距誤差和傳感器節(jié)點位置誤差的先驗信息融入算法中。仿真結(jié)果表明，WTLS算法與常用的兩步WLS算法相比，有很好的定位性能。

1 雙誤差條件下的TDOA目標(biāo)定位模型

1.1 目標(biāo)與傳感器節(jié)點之間的幾何關(guān)系

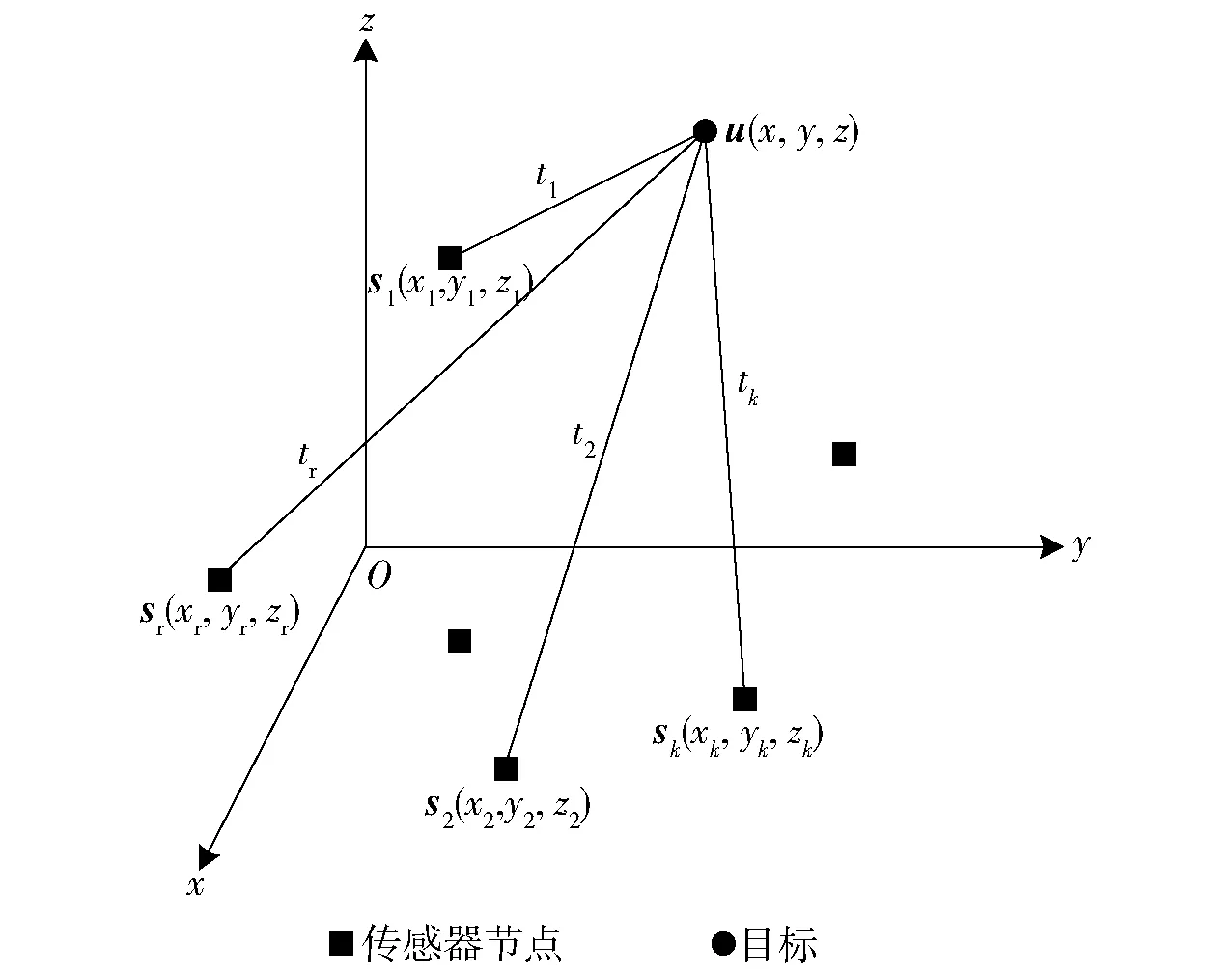
圖1 基于TDOA的目標(biāo)估計示意圖Fig.1 Target estimation based on TDOA

基于傳感器節(jié)點的目標(biāo)定位示意圖如圖1所示。假設(shè)M個傳感器節(jié)點的位置坐標(biāo)分別為sk=[xk,yk,zk]T，k=1,2,…,M，xk、yk、zk表示第k個節(jié)點位置坐標(biāo)的3個分量；單獨將另一個傳感器節(jié)點作為參考節(jié)點，用于計算目標(biāo)到其他節(jié)點和到參考節(jié)點的距離差，參考節(jié)點位置坐標(biāo)為sr=[xr,yr,zr]T，xr、yr、zr表示參考節(jié)點位置坐標(biāo)的3個分量；目標(biāo)位置坐標(biāo)為u=[x,y,z]T。則第k個節(jié)點接收到目標(biāo)u信號的到達時刻tk為

(1)

式中：c為水中聲速，c≈1 500 m/s；t0為目標(biāo)發(fā)射信號的時刻；nk為目標(biāo)信號到達第k個傳感器節(jié)點的時間估計誤差，且獨立同高斯分布。圖1中，t1、t2、tk、tr分別表示第1個、第2個、第k個節(jié)點和參考節(jié)點接收到目標(biāo)u信號的到達時刻。

當(dāng)目標(biāo)為非協(xié)作目標(biāo)或異步網(wǎng)絡(luò)時，目標(biāo)的發(fā)射信號時刻t0無法獲得，TDOA采用目標(biāo)到節(jié)點與參考節(jié)點時間差的方法，無需知道目標(biāo)發(fā)射信號的時刻t0.目標(biāo)信號到第k個節(jié)點與參考節(jié)點的時間差為

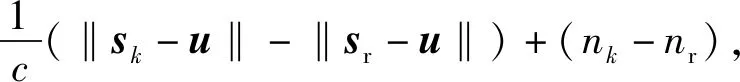
(2)

式中：nk、nr分別表示目標(biāo)信號到達第k個傳感器節(jié)點和參考節(jié)點的時間估計誤差。對于三維目標(biāo)定位，(2)式中的未知數(shù)u=[x,y,z]T的維數(shù)等于3，當(dāng)M≥3時可得雙曲方程(2)式的解；對于二維目標(biāo)定位，(2)式中的未知數(shù)u=[x,y]T的維數(shù)等于2，當(dāng)M≥2時可得雙曲方程(2)式的解。此即基于TDOA的傳感器節(jié)點目標(biāo)定位思想。

(2)式的本質(zhì)是求解由多個TDOA構(gòu)成的雙曲線的交點，當(dāng)M取等號時得到三元二次方程(三維)或二元二次方程(二維)，可直接求解；當(dāng)傳感器節(jié)點較多時，(2)式為超定非線性方程，不能直接應(yīng)用線性方法求解，若采用迭代搜索法則存在收斂性問題。文獻[16]提出一種參數(shù)變換的方法，通過二維坐標(biāo)中目標(biāo)、傳感器節(jié)點之間的距離及其幾何關(guān)系，利用一個中間未知量，將非線性方程轉(zhuǎn)化為偽線性方程。文獻[13]給出了含有目標(biāo)位置坐標(biāo)以及目標(biāo)到參考節(jié)點距離的超定偽線性方程組，并采用兩步WLS法給出該方程組的解析解。文獻[13]采用二維坐標(biāo)給出的結(jié)果也適用于三維坐標(biāo)。本文借鑒文獻[13]的思路，以二維坐標(biāo)為例，所得結(jié)果同樣也適用于三維坐標(biāo)。

在二維平面中，目標(biāo)到參考節(jié)點sr=[xr,yr]T的距離為

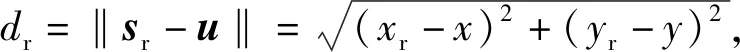
(3)

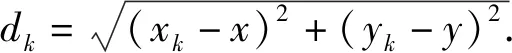
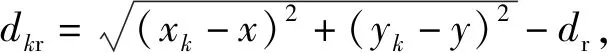
(4)

(4)式減去(3)式，得

(5)

式中：xkr=xk-xr；ykr=yk-yr.

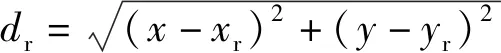
(6)

1.2 雙誤差條件下的TDOA目標(biāo)定位模型

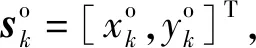
(Ga+ΔG)z=ha+Δh，

(7)

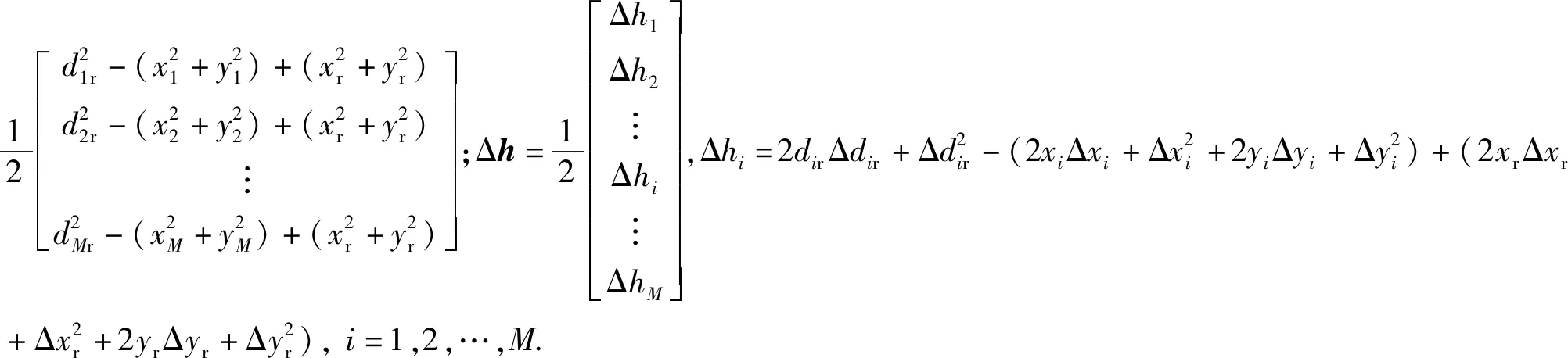
2 基于最小二乘的求解方法

高斯- 馬爾可夫定理研究表明：在線性回歸模型中，如果誤差滿足零均值、同方差且互不相關(guān)，則最小二乘法估計是回歸系數(shù)的最佳線性無偏估計。本文研究誤差不滿足高斯- 馬爾可夫定理要求時，用最小二乘方法對雙誤差條件下TDOA目標(biāo)定位模型((7)式)求解的性能。限于篇幅，本文僅分析目標(biāo)距離估計網(wǎng)絡(luò)較遠(yuǎn)的情況。

為了方便對比，在2.1節(jié)給出Chan算法的兩步加權(quán)最小二乘方法的求解步驟；在2.2節(jié)給出本文所提基于WTLS，包括推導(dǎo)協(xié)方差矩陣的表達式并給出定權(quán)方法，建立約束優(yōu)化模型，基于Lagrange乘數(shù)法推導(dǎo)迭代表示式，最后給出求解步驟。

2.1 兩步WLS方法

WLS方法忽略了模型(7)式中的節(jié)點自定位誤差包括乘性誤差，僅考慮距離差估計的測量誤差，則模型(7)式可表示為

Gaz=h，

(8)

式中：h=ha+Δh=

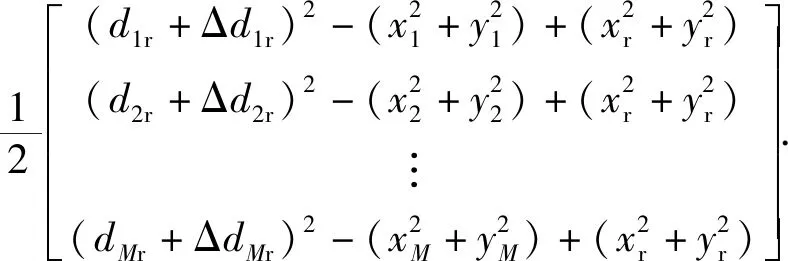
(8)式的求解問題可表示為如下優(yōu)化問題：

(9)

由于模型(8)式中的誤差僅是由距離估計誤差引起，則誤差可表示為

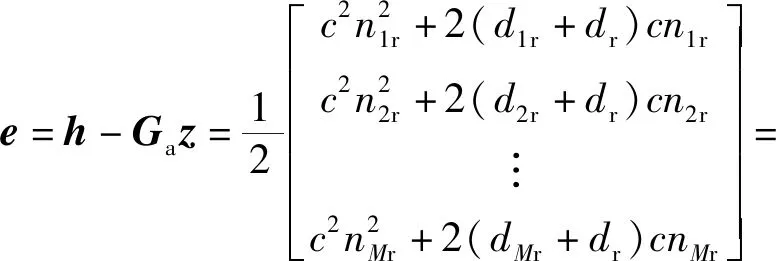
(10)

式中：B=diag(d1r+dr,d2r+dr,…,dMr+dr)，且BT=B；n=[n1r,n2r,…,nMr]T服從均值為0、協(xié)方差矩陣為Q的高斯分布；符號⊙表示Hadamard乘積。

由于dkr+dr?cnkr，忽略其高階項，e≈cBn也服從均值為0的高斯分布，其協(xié)方差矩陣可表示為

Σ=Cov(e,e)=E[eeT]≈
c2BE[nnT]BT=c2BQB，

(11)

式中：Cov(e,e)表示求e的協(xié)方差矩陣；E[·]表示·的數(shù)學(xué)期望。

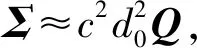
(12)

式中：z取決于Σ(或Q)的矩陣結(jié)構(gòu)，而與其縮放比例無關(guān)。考慮到z中dr與[x,y]T的相關(guān)性，Chan給出了兩步WLS的算法[13]。該算法的具體步驟如下：

步驟1利用WLS對模型(8)式計算，得到初始解

式中：za為z的估計值。由于目標(biāo)距離較遠(yuǎn)，可用Q代替Σ，得

步驟2利用步驟1的估計值重新構(gòu)造一組誤差方程組進行第2次估計。重構(gòu)的方程組為

由此得到優(yōu)化函數(shù)為

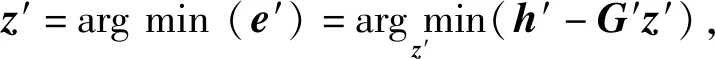
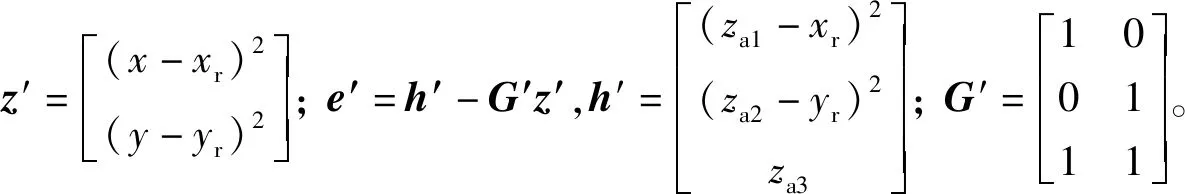
再次使用加權(quán)最小二乘法，得

z′≈(G′TB′-1GQ-1GB′-1G′)-1G′TB′-1GQ-1GB′-1h，

其中B′=diag[(za1-xr),(za2-yr),za3]。

步驟3Chan算法得到的最終目標(biāo)位置估計值為

2.2 WTLS方法

(7)式表示的雙誤差條件下TDOA目標(biāo)定位模型是變量(因變量和自變量)包含誤差(EIV)模型[17]，進一步可表示為

(13)

為了方便推導(dǎo)，忽略Δh中的高階項，得

由假設(shè)條件及(13)式可知，加性噪聲矩陣和乘性噪聲矩陣服從如下分布：

(14)

式中：vec(·)表示矩陣按列向量拉直；Σh和ΣG分別為Δh和ΔG的協(xié)方差矩陣，

(15)

(16)

G1、G2、G3為ΔG的3個列向量，其對應(yīng)的協(xié)方差矩陣分別為ΣG1、ΣG2、ΣG3，G1、G2、G3之間是相互獨立的，因此ΣG中除ΣG1、ΣG2、ΣG3外的元素都為M階零矩陣0.

由此可推導(dǎo)出

分別為協(xié)方差矩陣ΣG的3個分塊矩陣。

EIV模型的TDOA目標(biāo)定位問題可轉(zhuǎn)化為如下條件優(yōu)化問題：

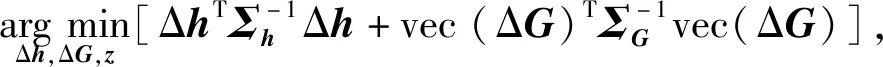
(17)

本文使用Schaffrin[18]等提出的方法進行定權(quán)，即要求協(xié)方差矩陣ΣG被分解為(18)式的形式：

ΣG=Qx?Q0，

(18)

式中：

(17)式所示的優(yōu)化問題可轉(zhuǎn)化為下列約束優(yōu)化問題：

(19)

本文按Lagrange乘數(shù)法求解，于是構(gòu)造目標(biāo)函數(shù)如下：

(20)

式中：拉格朗日因子λ∈RM×1.

對(20)式中的Δh、vec(ΔG)、λ和z分別求偏導(dǎo)數(shù)，并使其等于0，可以得到

(21)

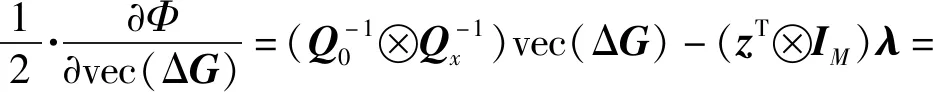
(22)

(23)

(24)

(21)式、(22)式代入(23)式，得

=[Σh+(TQ0)Qx]-1(ha-Ga).

(25)

(25)式代入(21)式及(22)式，得

Δ=-Σh[Σh+(TQ0)Qx]-1(ha-Ga)，
Δ=Qx[Σh+(TQ0)Qx]-1(ha-Ga)TQ0.

(26)

(25)式、(26)式代入(24)式，得

=(ha-Ga)T(Σh+(TQ0)Qx)-1·
Qx(Σh+(TQ0)Qx)-1(ha-Ga)，

(27)

(28)

通過推導(dǎo)可知，本文所提基于WTLS的方法充分利用了誤差的先驗信息得到估計值，但是WTLS問題目前無法得出解析解，只能通過迭代的方法進行數(shù)值求解。若得到測量值G=Ga+ΔG，h=ha+Δh，則算法迭代過程如下：

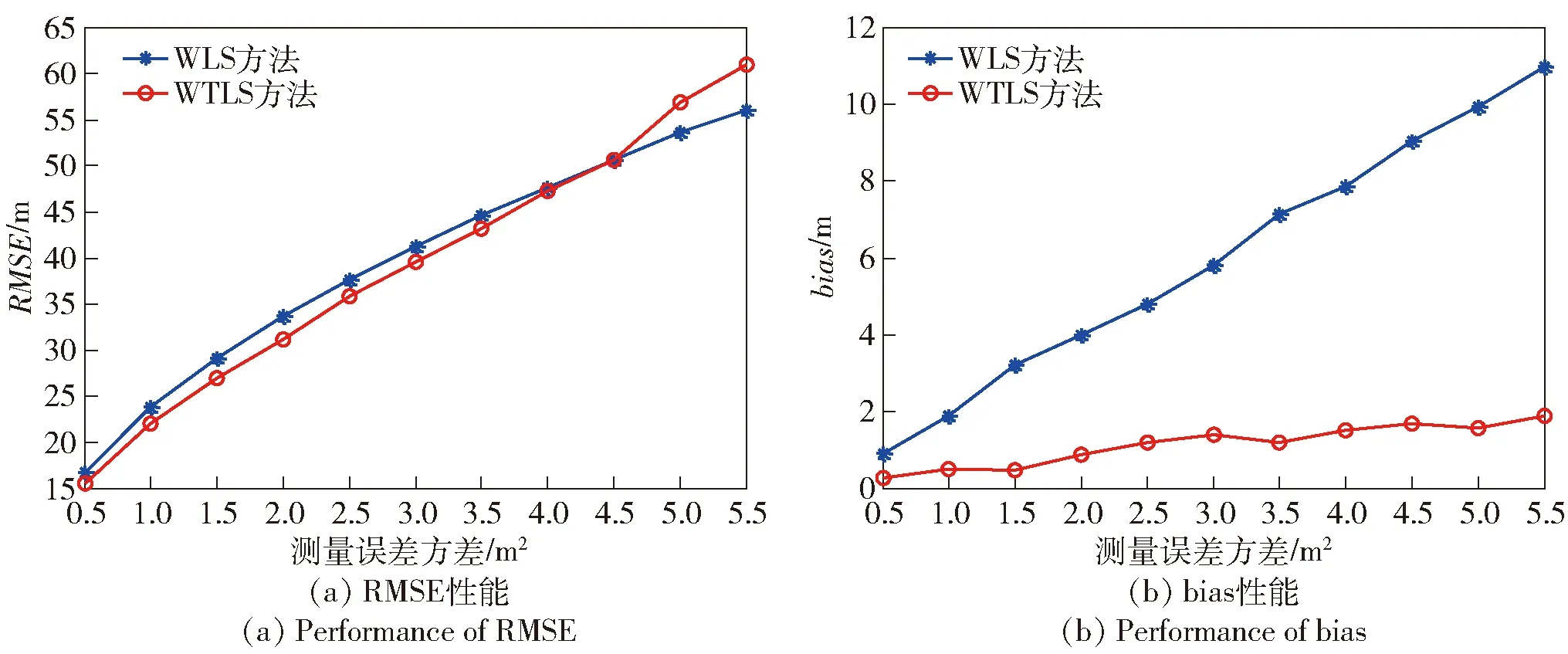
圖2 傳感器節(jié)點無誤差時測量誤差對估計性能的影響Fig.2 Influence of measured error on estimation performance when sensor node has no error

步驟1未知量的初次迭代值

(1)=(GT(Σh+((0)TQ0(0))Qx)-1G)-1·
GT(Σh+((0)TQ0(0))Qx)-1h.

步驟2給出迭代過程中要求解的兩個迭代量(i)和(i)，i表示迭代次數(shù)，

(i)=(h-G(i))T(Σh+((i)TQ0(i))Qx)-1·
Qx(Σh+((i)TQ0(i))Qx)-1(h-Ga(i))，
(i+1)=(GT(Σh+((i)TQ0(i))Qx)-1G-(i)Q0)-1·
GT(Σh+((i)TQ0(i))Qx)-1h.

步驟3重復(fù)步驟2，給出一個閾值ε,當(dāng)‖z(i+1)-z(i)‖<ε時，計算結(jié)束。

步驟4輸出結(jié)果z(i+1)的前兩項，即為u目標(biāo)真實位置的值。

3 定位方法性能及復(fù)雜度仿真和試驗

3.1 定位方法性能評價指標(biāo)

評價定位方法性能的指標(biāo)通常用均方根誤差(RMSE)和偏差(bias)，其定義分別為

(29)

(30)

3.2 誤差大小對估計性能影響的仿真及分析

不同誤差大小對定位性能影響的仿真結(jié)果如下：

1)節(jié)點位置無誤差時，測量誤差對目標(biāo)定位性能的影響如圖2所示。

2)節(jié)點位置誤差的方差分別為0.01 m2、0.50 m2和3.00 m2時仿真結(jié)果如圖3所示。

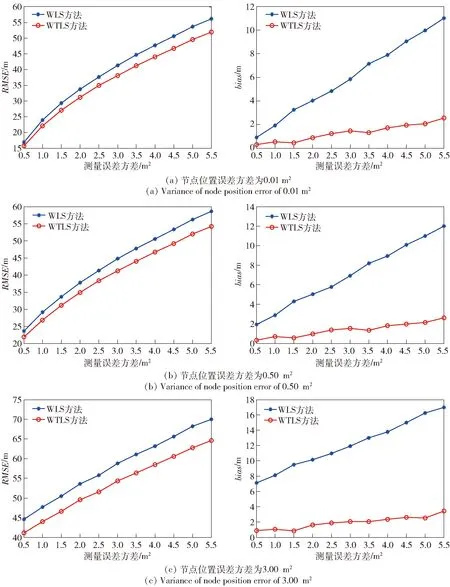
圖3 傳感器節(jié)點位置誤差方差一定時測量誤差對估計性能的影響(左為RMSE性能，右為bias性能)Fig.3 Influence of measured error on the estimation performance when the position error variance of sensor node is constant (left:performance of RMSE;right:performance of bias)

3)測量誤差分別為0.01 m2、0.50 m2和3.00 m2時的仿真結(jié)果如圖4所示。

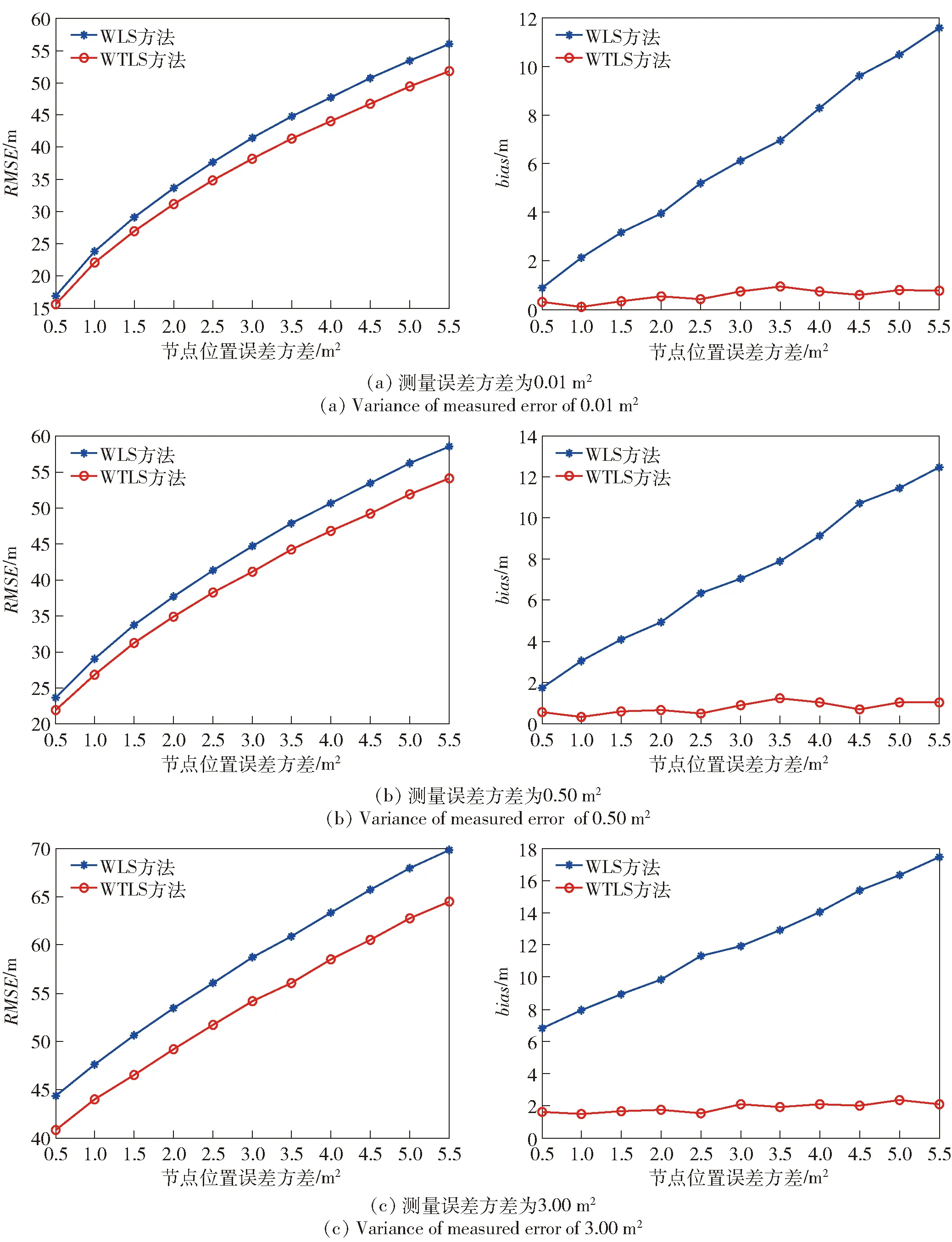
圖4 測量誤差方差一定時傳感器節(jié)點位置誤差對估計性能的影響(左為RMSE性能，右為bias性能)Fig.4 Influence of position error of sensor node on estimation performance when the measurement error variance is constant (left:performance of RMSE;right:performance of bias)

從圖2～圖4中可看出：隨著誤差的增大，兩種方法對節(jié)點估計的均方根誤差也隨著增大，WTLS方法的均方根誤差略小于WLS方法；WTLS方法的偏差比WLS方法的偏差小很多。究其原因，是因為WTLS方法的模型更準(zhǔn)確。

從圖2中可看出，當(dāng)節(jié)點位置準(zhǔn)確時，WTLS方法和WLS方法的均方誤差基本相當(dāng)，而WTLS方法的偏差比WLS方法小。這是因為WTLS方法的模型考慮了乘性誤差，而WLS方法的模型未考慮乘性誤差，即使Chan算法兩次運用最小二乘法，對估計偏差性能的提高有限。

對比圖3和圖4可以看出：節(jié)點位置誤差和測量誤差的大小對兩種方法的目標(biāo)估計均方根誤差影響基本相同，這是因為在雙誤差模型(7)式中的乘性矩陣和加性矩陣中均包含有節(jié)點位置誤差和測量誤差；當(dāng)測量誤差一定時，節(jié)點位置誤差的大小對WTLS方法的偏差影響較小，這是因為WTLS方法的模型更精確。

3.3 節(jié)點個數(shù)對估計性能影響的仿真及分析

節(jié)點位置誤差和測量誤差的方差均為0.50 m2，節(jié)點個數(shù)從3～12變化，3.2節(jié)中其他仿真條件不變時的仿真結(jié)果如圖5所示。

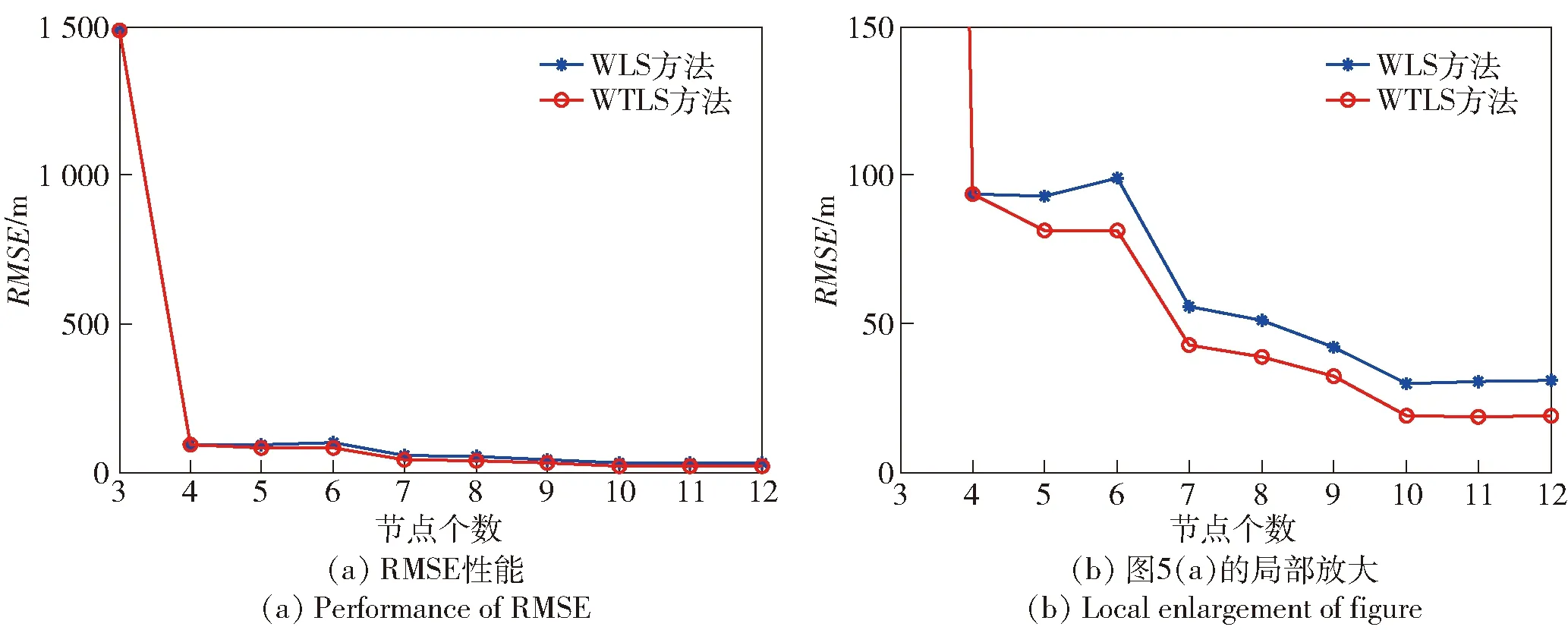
圖5 傳感器節(jié)點個數(shù)對估計性能的影響Fig.5 Influence of the number of sensor nodes on the estimation performance

由圖5可知，節(jié)點個數(shù)的多少對兩種方法性能的影響基本相當(dāng)。當(dāng)節(jié)點個數(shù)由3增加到4時，兩種估計方法的性能均有很大提升，但當(dāng)節(jié)點個數(shù)繼續(xù)增大時，估計性能提升值很小。這是因為雖然節(jié)點個數(shù)的提升可提高估計性能，但是每個節(jié)點都是有誤差的，節(jié)點的誤差又影響了估計的性能。

3.4 定位方法復(fù)雜度仿真和分析

對于WLS和WTLS兩種定位方法的復(fù)雜度，本文采用相對計算時間來衡量，在i5-6500處理器的Win7_64位臺式計算機上，用MATLAB2014b軟件完成復(fù)雜度比較的仿真。

表1 WLS和WTLS的相對計算時間比較Tab.1 Comparison of relative computation times of WLS and WTLS

表1中，對WLS和WTLS中ε取不同值時的相對計算時間進行了比較，將WLS的計算時間作為1.00，WTLS中ε=10、ε=5、ε=1、ε=10-11時的相對計算時間分別為1.33、1.43、1.50、1.98.從表1中的數(shù)據(jù)可以看出，WTLS的計算時間要多于WLS的計算時間，隨著閾值ε減小，WTLS的計算時間在增加，但同時定位性能也在改善。因此，算法定位性能和計算時間要統(tǒng)籌分析，根據(jù)需求選擇算法對應(yīng)的ε值。

3.5 定位方法的水池試驗和結(jié)果分析

為了驗證本文所提WTLS法的定位效果，在西北工業(yè)大學(xué)消聲水池進行試驗驗證。水池試驗現(xiàn)場和節(jié)點如圖6所示，其中：圖6(a)是水池試驗現(xiàn)場，水池長20 m、寬8 m、深7 m、水深6.8 m；圖6(b)是試驗用的節(jié)點，布放在水深3 m處，共有5個節(jié)點，將其中1個節(jié)點作為待定位的目標(biāo)，其他節(jié)點作為網(wǎng)絡(luò)節(jié)點。

圖6 水池試驗現(xiàn)場和節(jié)點Fig.6 Experimental site and node

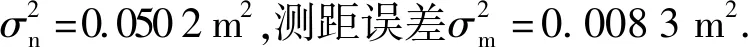
表2 WLS和WTLS試驗效果比較Tab.2 Comparison of experimental results of WLS and WTLS m

從表2中可以看出，WLS、WTLS方法的性能都比較好。除算法本身之外，本文設(shè)計的試驗節(jié)點具有偏差補償?shù)墓δ堋１?中，對比來看，在RMSE、bias方面，本文提出的WTLS定位效果都要比WLS定位效果好。

4 結(jié)論

針對水聲傳感器網(wǎng)絡(luò)目標(biāo)定位中傳感器節(jié)點位置誤差大不能忽略的情況，同時考慮測量誤差及傳感器節(jié)點位置誤差，本文構(gòu)造了雙誤差條件下的TDOA目標(biāo)定位模型。采用該模型，提出一種基于WTLS的求解算法，推導(dǎo)出協(xié)方差矩陣的表達式并給出定權(quán)方法。基于Lagrange乘數(shù)法，推導(dǎo)出迭代表達式，給出求解步驟。

本文所提方法在模型上同時考慮了兩種誤差，在求解方法上利用了誤差的先驗信息，仿真和水池試驗結(jié)果均表明：雙誤差條件下WTLS目標(biāo)定位方法的RMSE和bias均小于WLS方法的RMSE和bias.