基于多特征量的海雜波參數估計

何耀民，何華鋒，徐永壯，王依繁，蘇敬

(火箭軍工程大學 導彈工程學院，陜西 西安 710025)

0 引言

海雜波是指雷達在海面上形成的散射回波，海雜波受波浪、海風和潮汐等復雜環境的影響。為有效評估不同海況下彈載合成孔徑雷達(SAR)成像性能，迫切需要深入分析不同海況下的雜波模型。

關于海雜波模型的研究，主要采用統計分布方法，例如對數正態分布、Weibull分布和K分布等。由于K分布模型能兼顧海雜波的幅度分布特征和脈間相關性能，較其他模型更能準確反映海雜波的統計特性。Marier[1]、Conte等[2]分別利用球不變隨機過程(SIRP)法和零記憶非線性(ZMNL)變換法對海雜波進行了仿真。基于上述兩種方法，大多學者對其進行了應用或改進：Ritchie等[3]通過雜波數據的累積振幅求解虛警概率，估計海雜波的統計量；Watts[4]和Watts等[5-6]利用多普勒譜測量結果，分析了平均功率譜密度和極值振幅等主要特征，提出基于復合K分布的海雜波模型，并通過大量測試數據進行了模型驗證；Weinberg[7-8]利用相互獨立的高斯矢量加權乘積構造正交分量，提出計算更簡單的KK分布海雜波模型。

針對海雜波的模型參數，目前主要通過經驗公式或參數估計求解，常用的經驗公式有Ward模型[9]、Ryan模型[10]等。由于海雜波不僅受雷達頻率、入射余角、極化方式和分辨單元等固有屬性影響，還與風速、風向、海況、雨等自然因素緊密相關，因此針對實際作戰海域的某型彈載SAR，基于經驗公式的參數推導較難準確貼近真實海況。相比之下，基于實測數據的參數估計法更能反映具體海域的雜波特性。常用的參數估計法包括矩估計法、最大似然估計法和混合估計法等。Blacknell等[11]利用對數估計量法進行改進，可提高模型參數的估計精度；Bocquet[12]利用平均諧波構造閉形式的參數估計模型，避免了求解最大似然估計法中的高維非線性方程，從而簡化了計算過程；Balleri等[13]結合最大似然估計和分數矩法進行參數估計，并通過大量數據驗證了該混合模型的適用性。此外，也有學者將擬合度分析[14]、神經網絡[15]等方法運用于參數估計。

上述文獻都是通過各階矩的計算量或概率密度函數來吻合實測數據，通常能較好地反映出雜波的整體分布趨勢，具有一定的參考價值，但未能精確擬合海雜波幅度分布的峰值、幅度寬度等多個特征量。本文建立基于多特征量的參數估計法：首先建立基于SIRP法的海雜波模型，然后針對傳統參數估計法對特征點擬合效果差的問題，構造反映海雜波幅度分布的4個特征量，并分析其對尺度參數、形狀參數的影響；進而利用實測數據和反向傳播(BP)神經網絡求解模型參數，建立海雜波幅度分布模型；最后，通過不同海況下后向散射系數確定海雜波的信號功率，為評估不同海況下彈載SAR成像性能提供了雜波模型。

1 基于SIRP法的海雜波模型

K分布模型[16]由散斑分量(受瑞利分布影響)和調制分量(受伽馬分布影響)組成，該模型能兼顧海雜波的幅度分布特性和脈間相關性能，是目前使用較廣泛的海雜波模型。

1.1 幅度分布特性

海雜波的幅度分布特性可由其概率密度函數[17]表示，如(1)式所示：

(1)

式中：f(x;υ,α)為概率密度函數，x為海雜波的幅度，υ為形狀參數，α為尺度參數；Γ(υ)為伽馬函數；Kη為η階貝塞爾函數。通常，υ趨于0時有較長拖尾，趨于∞時逼近瑞利分布。

1.2 時間相關性

海雜波的時間相關性可由其高斯功率譜密度[18]表示，如(2)式所示：

(2)

式中：S(f)為高斯功率譜密度，f為海雜波頻率；fD為平均多普勒頻移；σf=2σ/λ為雜波頻譜均方根，σ為雜波速度的均方根，λ為雷達波長。

由于彈載SAR常采用頻率捷變方式抑制海雜波(頻率捷變對海雜波譜具有白化作用)，可較大程度削弱其相關性[19]；且不同海況下雜波對成像性能的影響主要體現在信干比、圖像斑點、分辨率等功率方面。基于上述兩點考慮，本文采用經驗公式[9]推導σ、fd，重點考慮形狀參數和尺度參數的求解。

1.3 基于SIRP法的海雜波模型

在綜合分析海雜波幅度分布特征和時間相關性的基礎上，建立基于SIPR法[1]的海雜波模型，如圖1所示。圖1中：k為海雜波序列數；Y(k)為散斑分量；Z(k)為實白高斯噪聲；S(k)為調制分量。

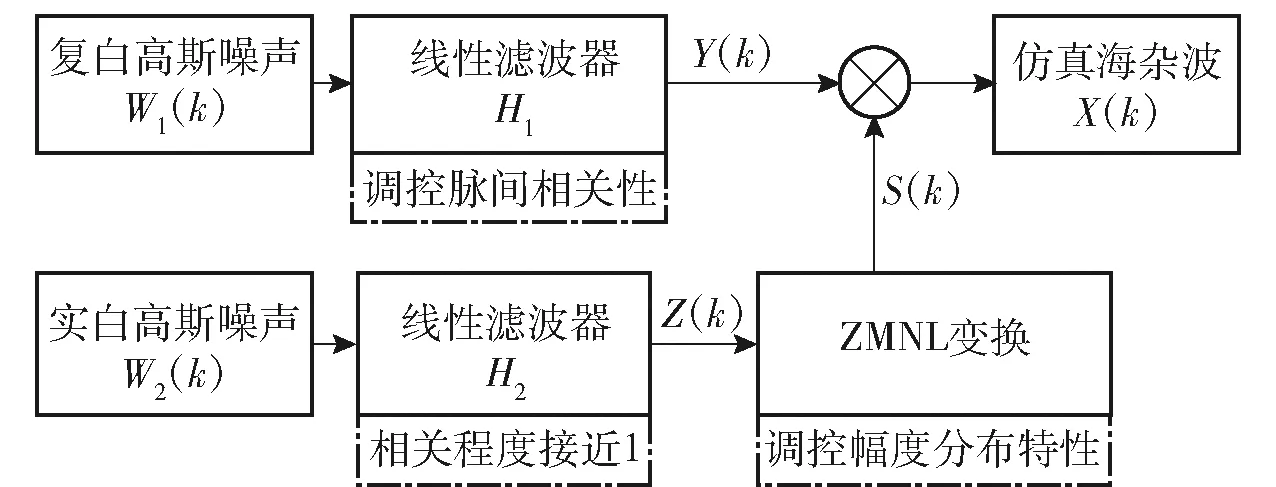
圖1 基于SIRP法的海雜波模型Fig.1 Sea clutter model based on SIRP method

如圖1所示，SIRP法是模擬雷達的相參機理產生W1、W2兩路正交信號：一路由線性濾波器H1處理復白高斯噪聲W1(k)，可由高斯功率譜S調控產生散斑分量Y(k)，該分量主要調控海雜波的脈間相關性；另一路由線性濾波器H2調控實白高斯噪聲W2(k)生成Z(k)，使其相關性接近1，故海雜波的相關性主要受線性濾波器H1影響；再由ZMNL變換控制雜波的幅度分布特征，可由概率密度函數f調控Z(k)生成調制分量S(k)；最后，由散斑分量Y(k)和調制分量S(k)合成海雜波X(k)。

基于上述仿真建模，海雜波參數主要包括形狀參數v、尺度參數α.本文將采用基于多特征量的參數估計法，并結合實測數據進行求解。

2 基于多特征量的參數估計

傳統參數估計法包括矩估計法、最大似然估計法和混合估計法等。此類方法通常利用各階矩的計算量或概率密度函數來吻合實測數據，雖然能較好地反映雜波的整體分布趨勢，但對于多個海雜波特征量的擬合效果欠佳。因此，本文通過構造反映海雜波幅度分布的4個特征量，建立基于多特征量的參數估計模型。

2.1 海雜波幅度分布的特征量

在評估不同海況下彈載SAR成像性能時，從幅度分布、信號功率和實測數據波動大等方面考慮，相比于提高海雜波的整體吻合度，把握住其幅度分布的多個特征點更具有實際意義。因此，本文借鑒雷達回波信號的幅度分布圖[20]，構造出反映海雜波幅度分布的4個特征量，如圖2所示。

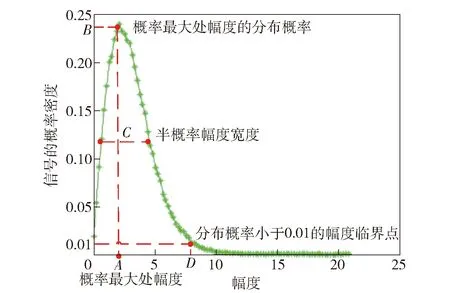
圖2 幅度分布函數的4個特征量Fig.2 Four characteristic quantities of amplitude distribution function

觀察圖2可知，4個特征量分別為：1)分布概率最大處所對應的幅度A；2)概率最大處幅度的分布概率B；3)半概率幅度寬度C；4)分布概率小于0.01的幅度臨界點D.通過構造上述4個特征量，即可確定海雜波的幅度分布函數。

2.2 模型參數分析

2.2.1 尺度參數

尺度參數α反映了海雜波回波信號的功率特性，即參數越大、幅度越高[21-22]。根據第1節中的海雜波模型，令σ=1、fD=0 Hz、υ=2，α為單一變量進行仿真，分析其對4個幅度特征量的影響，各特征量的變化趨勢如圖3所示。

觀察圖3(a)、圖3(c)、圖3(d)可知，當尺度參數α在[0，4]范圍內增大時，概率最大處的幅度A、半概率幅度寬度C和幅度臨界點D均為單調遞增；觀察圖3(b)可知，雜波幅度最大處所對應概率B為單調遞減。結合尺度參數與幅度間聯系[21-22]可知，圖3(a)、圖3(c)、圖3(d)的仿真結果與α的物理意義相吻合。另外，由圖3(b)可見，尺度參數越大時，雜波幅度分布趨勢越平緩。為證明上述結論在其他參數情況下仍然適用，令σ=2、fD=100 Hz、υ=3，所得仿真結果與圖3十分相似，從而表明上述關于尺度參數分析的正確性。

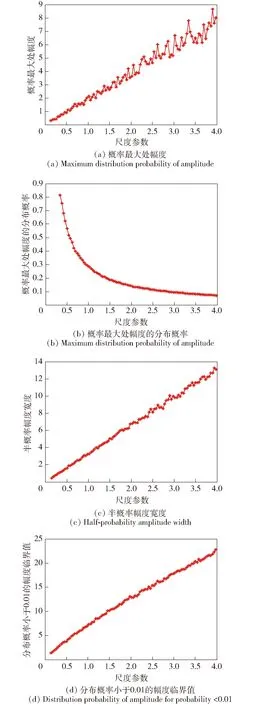
圖3 尺度參數對海雜波幅度分布的影響Fig.3 Influence of scale parameter on amplitude distribution of sea clutter

2.2.2 形狀參數

目前常用的形狀參數ν推導公式[17]如下：

(3)

式中：φ為入射余角；SA為有效受照區域；δ為風向參數，在順風時δ為-0.34、逆風時δ為0.34；K1為極化方式參數，在水平極化時K1為2.09、垂直極化時K1為1.39.

由(3)式可知：形狀參數通常與入射余角、照射區域、風向、極化方式等因素有關，與信號幅度的聯系不太緊密(已通過BP神經網絡仿真驗證：若單獨通過幅度分布預測形狀參數，則其決定系數<0.8)；另外，對于K分布海雜波，通常認為雜波平均功率為4υα2，即形狀參數ν與尺度參數α相關聯[17]。基于以上分析，為增強形狀參數和4個幅度分布特征間的聯系，將尺度參數作為限定因素加入幅度分布特性中。

2.3 BP神經網絡求解參數

通過2.2節分析可知：形狀參數ν、尺度參數α與幅度分布函數的4個特征量是緊密相關的，因此可通過求解二者間的定量關系確定模型參數。但由于ν、α與4個幅度分布特征間為非線性、高階次對應關系，直接求解存在較大難度，故選用BP神經網絡來挖掘數據間的定量關系。

BP神經網絡[23-25]由一個輸入層、若干個隱含層和一個輸出層組成，各層均有一個或多個神經元節點。該模型利用誤差逆傳播算法，通過調整各層連接權值，從而使目標輸出和實際輸出滿足在一定誤差范圍內。本文參考遺傳算法[26]建立BP神經網絡模型，將貝葉斯正則化方法作為模型訓練函數，如(4)式所示：

F=φEw+βEd，

(4)

式中：F為模型訓練函數；Ew為整個訓練網絡的權值平方和；Ed為各層網絡誤差值；φ和β為正則化系數。利用BP神經網絡求解模型參數的算法流程如圖4所示，其中A0、B0、C0、D0為實況海雜波數據的4個特征量。

圖4 BP神經網絡的算法流程圖Fig.4 Algorithm flow chart of BP neural network

在建立上述BP神經網絡模型的基礎上，可利用實測數據求解尺度參數和形狀參數，從而確定海雜波的幅度分布模型。

2.4 不同海況的信號功率

描述海表面時，通常采用數字等級表示海表面狀態的惡劣程度。一般認為海表面狀態和風速的關系如下：只有當風在足夠大風浪區且持續足夠長的時間時，才能激起一個充分發展的海表面[20]，此時浪高和風速的關系如表1所示。

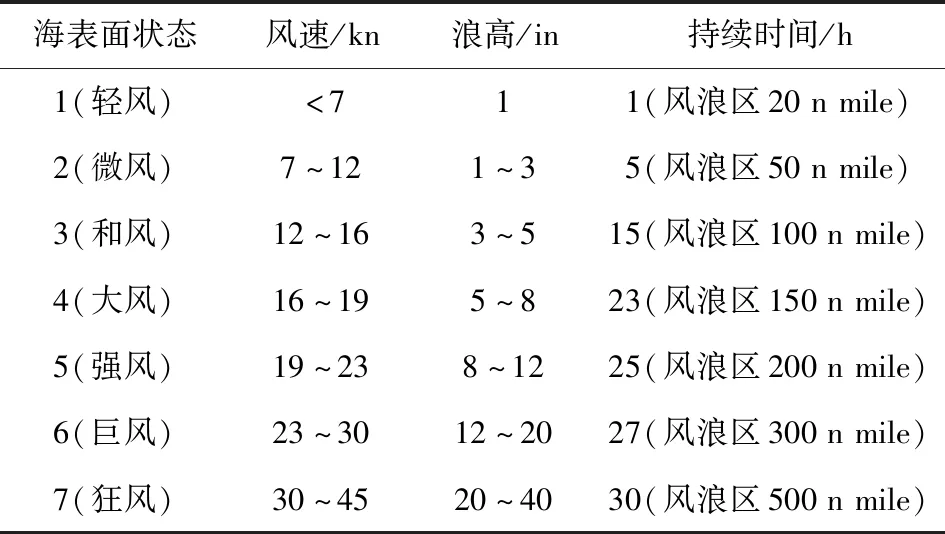
表1 海表面描述Tab.1 Sea surface description

Skolnik在雷達手冊[20]中指出：海雜波信號強度隨入射余角增大而增大，隨風速(或海表面狀態)增強而增強。另外，工程應用中通過利用后向散射系數計算信干比。因此，本文采用后向散射系數分析不同海況下雜波的信號功率。

SAR圖像的信雜比計算公式如下：

(5)

式中：Ps為雷達信號功率；Pc為雜波功率；σr為打擊目標的雷達散射截面；γ為入射余角；σ0為海雜波的后向散射系數；ρr為SAR距離向分辨率；ρa為SAR方位向分辨率。因此，在獲取不同海況下后向散射系數的基礎上，通過(5)式求解信干比，可確定不同海況下雜波的信號功率，進而可為有效評估不同海況下彈載SAR成像性能提供海雜波模型。

3 模型仿真

利用基于多特征量的參數估計法仿真海雜波模型。首先，分析中國人民解放軍海軍航空大學在中等入射余角、2級海況下測量的Ku波段數據[27]，按照圖4中的BP神經網絡求解該海況下雜波模型；然后，利用周平等通過機載海面散射試驗測量的Ku波段數據[28]，獲得在不同海況下的Ku波段后向散射系數；最后，結合2級海況雜波模型和不同海況下的雜波功率，實現不同海況下的雜波仿真。

3.1 海雜波的幅度分布模型

3.1.1 實測數據

本文中的2級海況雜波數據[27]來自高分辨率Ku波段雷達，信號脈寬為10 μs，距離向分辨率為1.875 m，入射余角44°，其幅度分布曲線如圖5所示；根據第2節中對幅度分布函數的分析求解4個特征量，如表2所示。

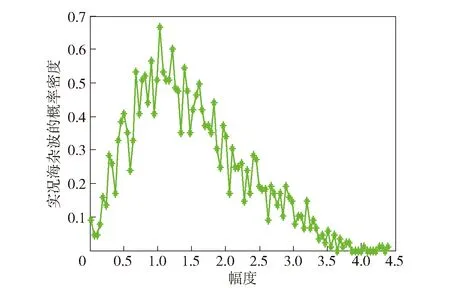
圖5 實況海雜波的幅度分布曲線Fig.5 Amplitude distribution curve of real sea clutter

表2 幅度分布函數的4個特征參數Tab.2 Four characteristic quantities of amplitude distribution function

注：概率最大處的概率取相鄰3點均值。

3.1.2 神經網絡訓練

利用第1節的海雜波模型，通過改變形狀參數、尺度參數，仿真得出32組不同參數下的海雜波；求解各組海雜波幅度分布的特征量(令概率最大處幅度、概率最大處幅度的分布概率、半概率幅度寬度、概率小于0.01的幅度臨界點分別為A、B、C、D)，如表3所示。

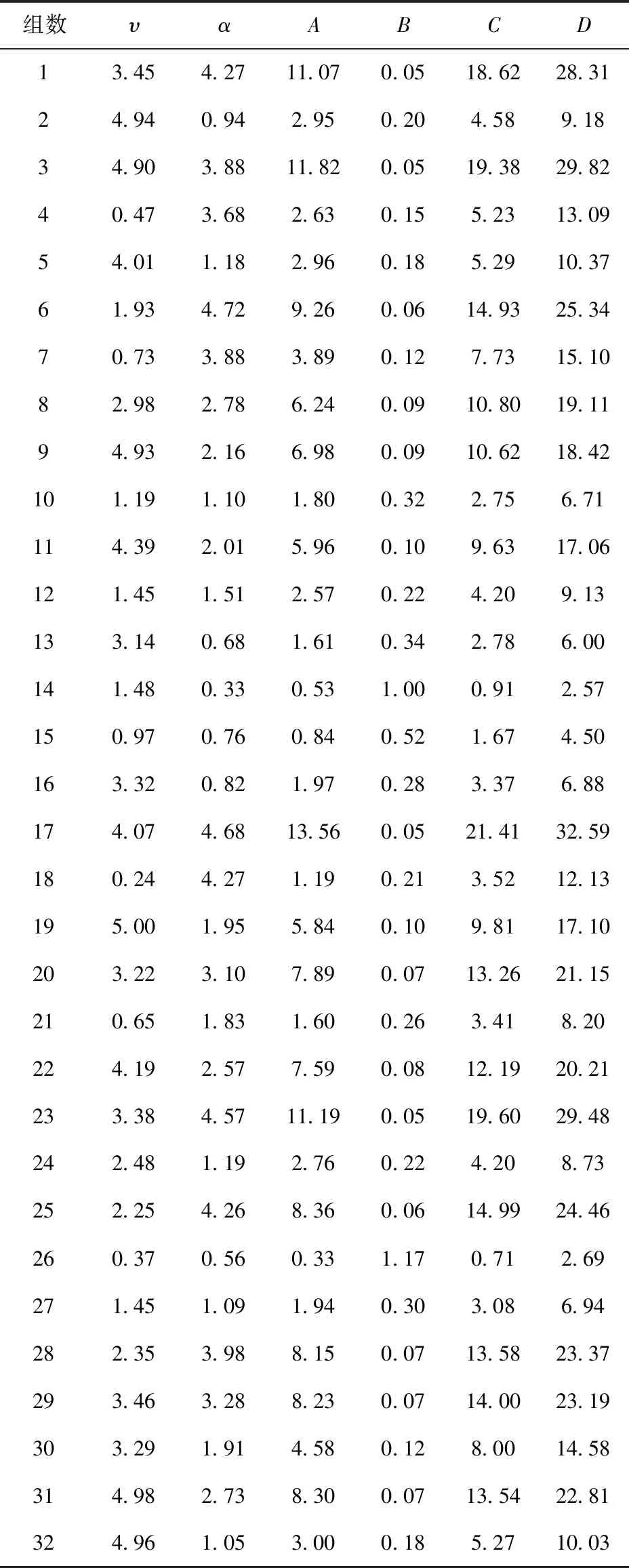
表3 各組海雜波幅度分布函數的特征參數Tab.3 Characteristic parameters of amplitude distribution of sea clutter in each group

3.1.3 求解海雜波模型參數

1)模型1訓練。將表3中前28個數據作為訓練樣本、后4個數據作為測試樣本，A、B、C、D為輸入、尺度參數α為輸出；確定輸入、輸出層的神經元個數分別為4和1；隱含層數為1、神經元數量為7，學習效率為0.01、訓練次數為1 000、誤差上限為0.000 1.可得到連接權值W1、閾值S1，完成模型1的訓練。

2)模型2訓練。參考模型1，將輸入擴增為A、B、C、D+α，輸出為形狀參數υ；輸入層的神經元個數改為5，其余參數不變。可得到連接權值W2、閾值S2，即完成模型2的訓練。

利用訓練好的BP神經網絡，分別將歸一化訓練、測試樣本作為輸入，利用Bootstrap[29]將數據擴充100倍后，求其預測值；將預測值與實際值進行對比，并用決定系數R2[30]檢驗模型好壞，決定系數R2計算公式如下：

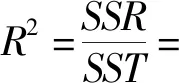
(6)

式中：SSR為回歸平方和；SST為總平方和；N為測試樣本個數；SA為模型預測值；SB為樣本原始值。當決定系數R越高時，模型評估的變化趨勢越接近真實值。利用訓練好的BP神經網絡對尺度參數、形狀參數進行預測，其決定系數分別為0.992和0.994，具體如圖6、圖7所示。

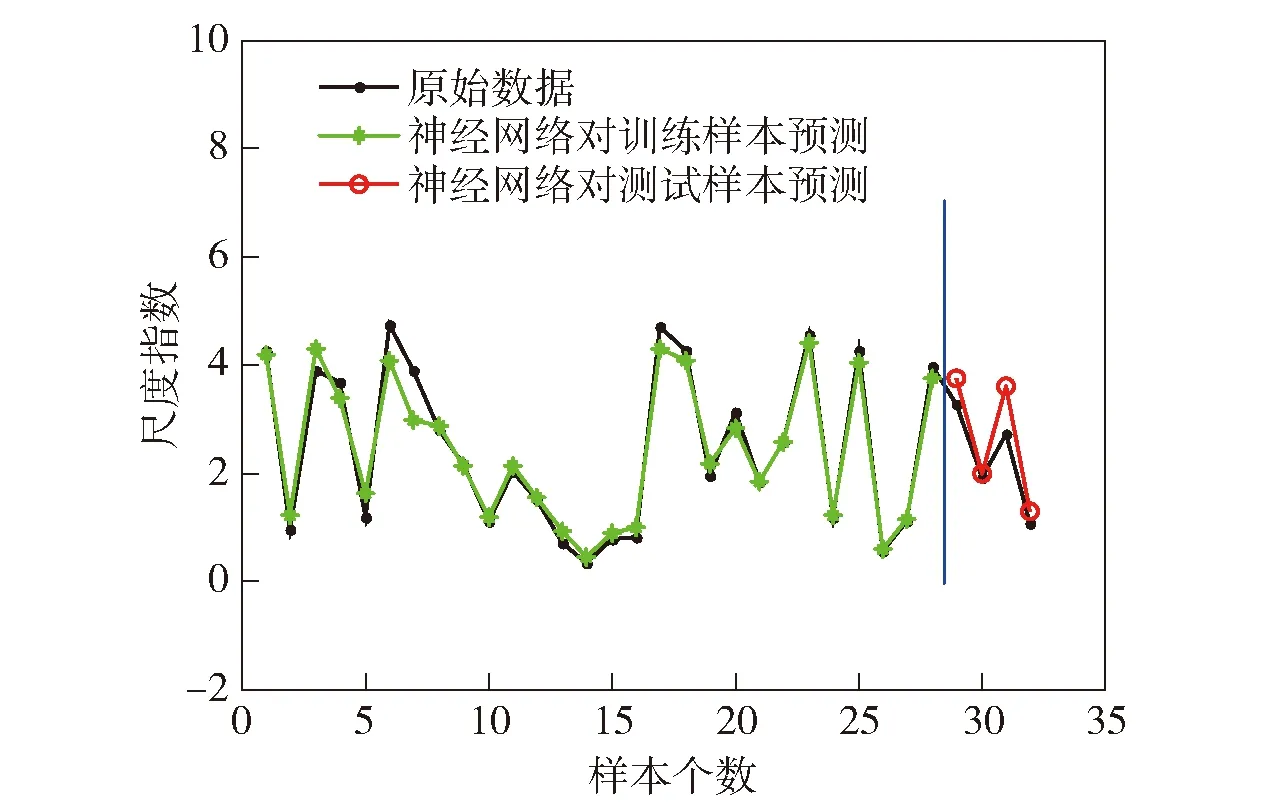
圖6 神經網絡對尺度參數的預測Fig.6 Prediction of scale parameter by BP neural network

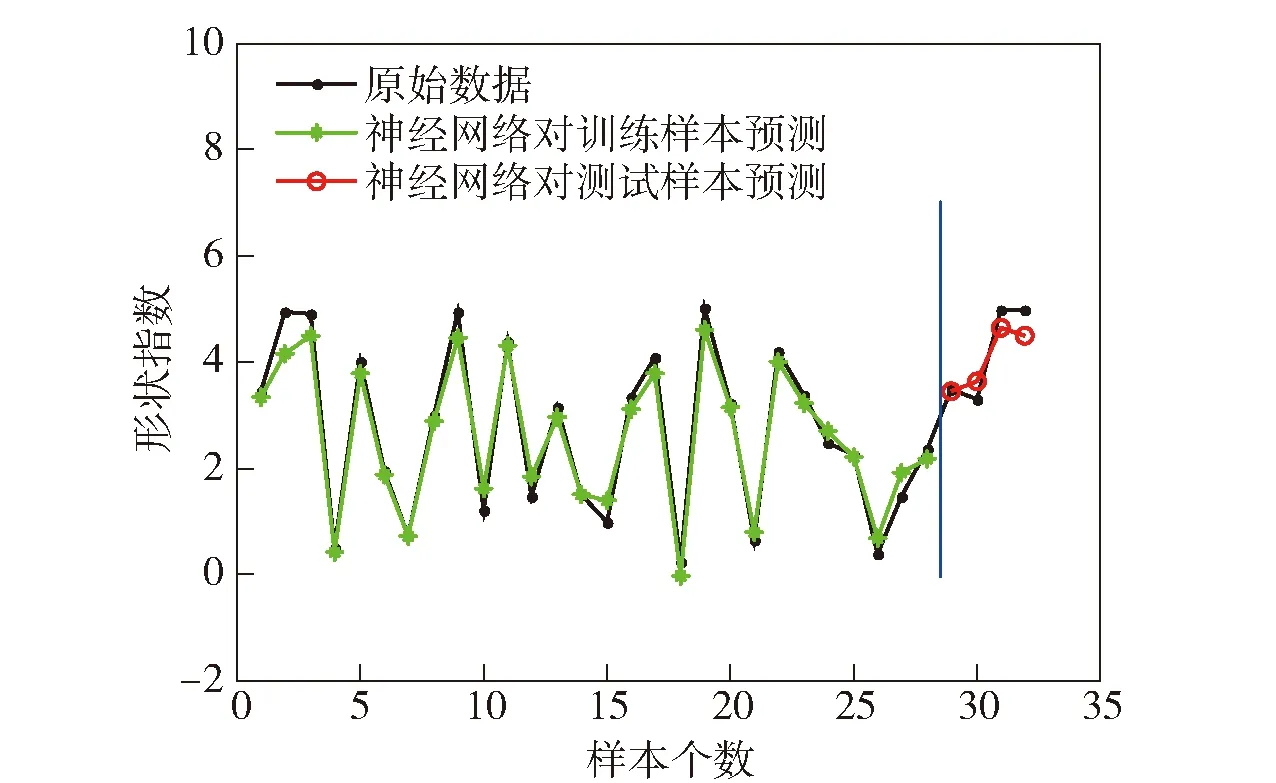
圖7 神經網絡對形狀參數的預測Fig.7 Prediction of shape parameter by BP neural network

最后，利用完成訓練的BP神經網絡，將表2中的A0、B0、C0、D04個特征量作為模型輸入，求解海雜波的模型參數ν和α，如表4所示。

另外，若單獨利用4個特征參數求解形狀參數ν，則其決定系數僅為0.784，從而驗證了2.2節中關于形狀參數分析的合理性。

3.2 不同海況的信號功率

3.2.1 后向散射系數

我國目標與環境電磁散射輻射國防科技重點實驗室在我國舟山海域開展了機載海面散射測量試驗[28]，其雷達為Ku波段、飛行時速為200～250 km/h、入射余角為20°～90°.該試驗在順風、逆風條件下獲得了2級、3級、4級海況的后向散射系數，如圖8所示。

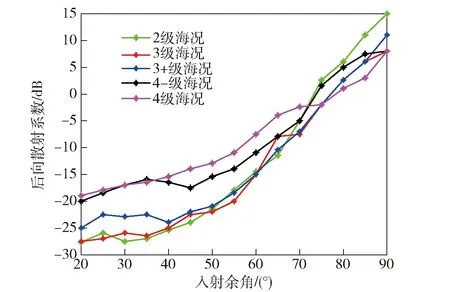
圖8 不同海況下雜波的后向散射系數Fig.8 Back-scattering coefficients under differentsea conditions

根據圖8中的實測數據，當入射余角為45°時，不同海況(2級、3級、3+級、4-級、4級)的后向散射系數分別為-24.0 dB、-22.5 dB、-22.0 dB、-17.5 dB、-14.0 dB.

3.2.2 不同海況下的信干比

當彈載SAR打擊目標時，令σr為25 dBm2、ρr為5 m、ρa為15 m，根據(5)式計算不同海況下信干比，如表5所示。

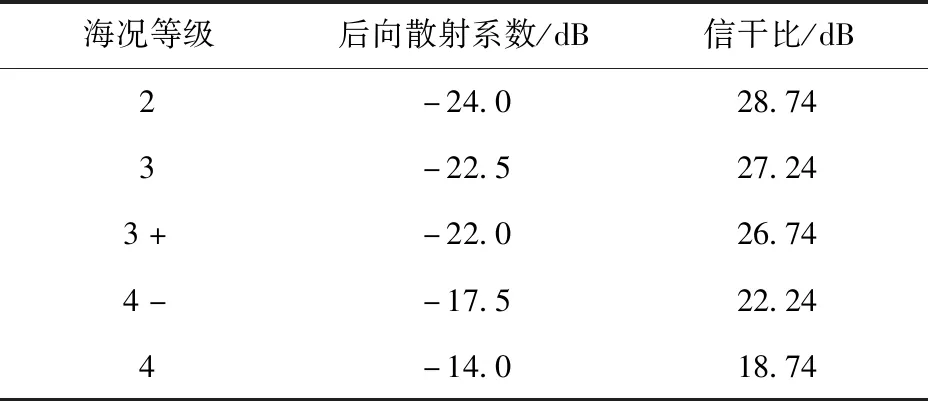
表5 不同海況下信干比Tab.5 Signal-to-interference ratios under different sea conditions

利用上述海雜波幅度分布和不同海況下雜波功率，即可實現不同海況下的雜波仿真，從而為評估不同海況下彈載SAR成像性能提供模型基礎。

3.3 方法對比

針對3.1節中海雜波幅度分布模型，分別利用經驗公式[9]和混合估計法[13]求解其形狀參數、尺度參數，而其雜波速度均方根、多普勒頻移則由經驗公式[9]獲取(σ=1，fD=24 Hz)。比較3種方法和真實海雜波的幅度分布特征，如圖9所示。

圖9 不同方法下海雜波幅度分布特性曲線Fig.9 Amplitude distributions of sea clutter estimated by different methods

從定性角度分析：如圖9所示，本文算法(綠色曲線)和混合估計法(藍色曲線)的幅度分布與實測數據(黑色虛線)基本相符，但混合估計法的概率最大處所對應幅度A偏差更大，且半概率幅度寬度C偏小；另外，相比本文算法和混合估計法，基于經驗公式(紅色曲線)的估計結果最不理想。

從定量角度分析：用平均相對誤差E[27]進行對比(E<0.5為有效擬合)，計算公式如下：

(7)

式中：X為實測數據；Q為估計值；n為數據個數。另外，按照2.1節計算各方法下仿真海雜波幅度分布的4個特征量，如表6所示。

表6 3種參數估計方法對比Tab.6 Comparison of estimated results of three methods

觀察表6可知，本文算法和混合估計法在平均相對誤差E、概率最大處幅度所對應概率B、概率小于0.01的幅度臨界點D都較為近似；但對比表4中實測數據的概率最大處幅度A和半概率幅度寬度C發現，本文算法在A和C的擬合更優于混合估計法，從而表明了本文算法的性能更佳。

4 結論

本文分析了海雜波模型中的形狀參數、尺度參數對其幅度分布特性的影響，提出了基于多特征量的參數估計法。結合數學仿真和經驗公式的手段分析可知：模型的尺度參數ν、形狀參數α與幅度分布函數的4個特征量是緊密相關的；利用實測數據和BP神經網絡先后求解尺度參數和形狀參數，建立了海雜波的幅度分布模型；在分析不同海況下后向散射特性基礎上，利用信干比實現不同海況下的雜波仿真，為有效評估不同海況下彈載SAR成像性能提供了模型依據。下一步將重點研究如何科學建立不同海況下成像性能的評估體系。