基于BOA-ELM的混凝土抗壓強度預測研究

吳小平　李元棟　張英杰　阮映輝　劉志文

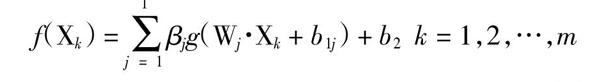
摘? ?要：為控制控制混凝土生產成本，在混凝土拌和期限制抗壓強度不足的缺陷構建產出，可以有效降低原料的浪費，是節能降耗的關鍵方法之一。針對混凝土抗壓強度的傳統測量方法嚴重滯后的問題，提出了基于貝葉斯優化極限學習機（BOA-ELM）的混凝土抗壓強度預測方法。首先，分析了混凝土拌和過程中對抗壓強度預測值實時獲得的需求。以各物料的用量為分析基礎，28天標準養護后混凝土抗壓強度值為預測目標，設計了基于極限學習機的強度預測模型。其次，為進一步提高模型的穩定性以及準確行，提出基于貝葉斯優化的極限學習機模型，根據模型超參數的分布特征，以高斯過程作為超參的先驗分布，預測誤差最小化作為目標，尋找最優的模型超參。最后，在實際施工產生的C50標號混凝土數據集上測試文中模型，并對比分析了其他預測模型和尋優算法。結果表明，結合了貝葉斯優化的極限學習機預測模型相較于經典算法具有更高的預測準確性和模型訓練的高效性。

關鍵詞：混凝土;抗壓強度預測模型;極限學習機;貝葉斯優化;軟測量

中圖分類號：TU528.1? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?文獻標識碼：A

Prediction of Concrete Compressive Strength Based on BOA-ELM

WU Xiao-ping1，LI Yuan-dong2？覮，ZHANG Ying-jie2，RUAN Ying-hui3，LIU Zhi-wen4

（1. Highway Administration of Zhejiang Province，Hangzhou，Zhejiang 310009，China;

2. College of Computer Science and Electronic Engineering，Hunan University，Changsha，Hunan 410082，China;

3. Zhejiang Taizhou Coastal Expressway Co.，Ltd.，Taizhou，Zhejiang 318000，China;

4. College of Civil Engineering ，Hunan University，Changsha，Hunan 410082，China）

Abstract：In order to control the cost of concrete，it is one of the key methods to save energy and avoid the waste of materials by limiting the output of defects whoes compressive strength is not up to standard，during the concrete mixing period. Because the traditional measurement method for concrete compressive strength is seriously lagging，the prediction method of concrete compressive strength based on extreme learning machine Bayesian optimized（BOA-ELM） is proposed. Firstly，the real-time demand of the value of the compressive strength predicted during the concrete mixing process is analyzed. Based on the analysis of the amount of each material and the compressive strength of the concrete after 28 days of standard curing ，the strength based on the extreme learning machine is designed. Secondly，in order to further improve the stability and accuracy of the predictive model，a extreme learning machine model Bayesian optimized（BOA-ELM） is proposed. According to the distribution of the model hyperparameters，the Gaussian process is used as the prior distribution ，and take prediction error minimized as the target，to find the best model super parameters. Finally，the model is tested on the C50 concrete dataset generated by the actual construction，and other prediction models and optimization algorithms are compared and analyzed. The results show that the extreme learning machine prediction model combined with Bayesian optimization has higher prediction accuracy and more efficiency of model training than classical algorithms.

Key words：concrete;prediction model of compressive strength;extreme learning machine;Bayesian optimization algorithm;soft-sensor

隨著建筑行業的發展，作為土木施工的主要材料之一的混凝土每年要消耗19.1億立方米之多。隨著各地對環境保護意識的增強，砂石的開采、運輸管理逐步規范化，混凝土原料的采購成本也隨之增加。如何合理控制混凝土生產成本成為土木行業的重要問題。混凝土的抗壓強度是結構設計和施工的重要參考指標[1]，按照傳統的方法，需要經過混凝土試塊壓制、28天養護室養護、壓力機壓力測試的漫長實驗獲得。如若該批次混凝土澆筑構件抗壓強度未達到規定標準，則廢除重筑。不僅浪費了原料，還延誤了工期，甚至影響施工安全。如果可以在混凝土拌和期間及時獲得預期強度，利于及時采取加固、補強措施，對于提高施工的質量和進度，避免物料浪費節約成本具有實用價值。

混凝土抗壓強度受物料、養護時間等多種因素影響，且成動態非線性。致使19世紀基于經驗構建的解析模型都有不同方面的局限性[2-3]。隨著人工智能方法的發展，混凝土抗壓強度預測研究領域涌現出多種智能模型，準確性更高的神經網絡[4]、支持向量機[5]及其衍生建模方法[6]被大量應用。但支持向量機核函數參數、規則化系數等設置較為復雜，核函數必須滿足Mercer條件。神經網絡方法需要大量數據進行訓練，且基于梯度下降的訓練速度較慢。為了能夠實時獲得混凝土預期抗壓強度強度，即時修正不滿足預期的拌和料，預測模型的內部參數復雜度一定要低、訓練效率一定要高。為此，嚴東等提出基于特征提取和極限學習機的軟測量方法[8]，并對混凝土抗壓強度的軟測量問題進行了實驗研究，驗證了所提方法的有效性，彌補了以上方法的不足，提高了訓練精度，縮短了訓練時間。

預測模型的泛化性能較大地受核參數、隱藏層節點數的影響，恰當的參數設置可以較大地提高模型的預測精度。目前廣泛使用的調參方法包括人工手動調參、網格搜索[9]以及如粒子群[10]、遺傳算法[11]等智能優化算法。手動調參繁瑣且依賴經驗，網格搜索以及智能優化算法大量占用計算資源和內存資源，模型訓練時效性較差。

綜上，為彌補上述建模以及超參尋優方法的不足，提出了基于貝葉斯方法來優化極限學習機超參數的混凝土抗壓強度軟測量方法。該方法采用了貝葉斯方法高效地優化對模型泛化性能具有較大影響的超參數，避免了手動調參的繁瑣、智能優化調參的費時費資源，并充分利用了極限學習機的高效性。

1? ?極限學習機

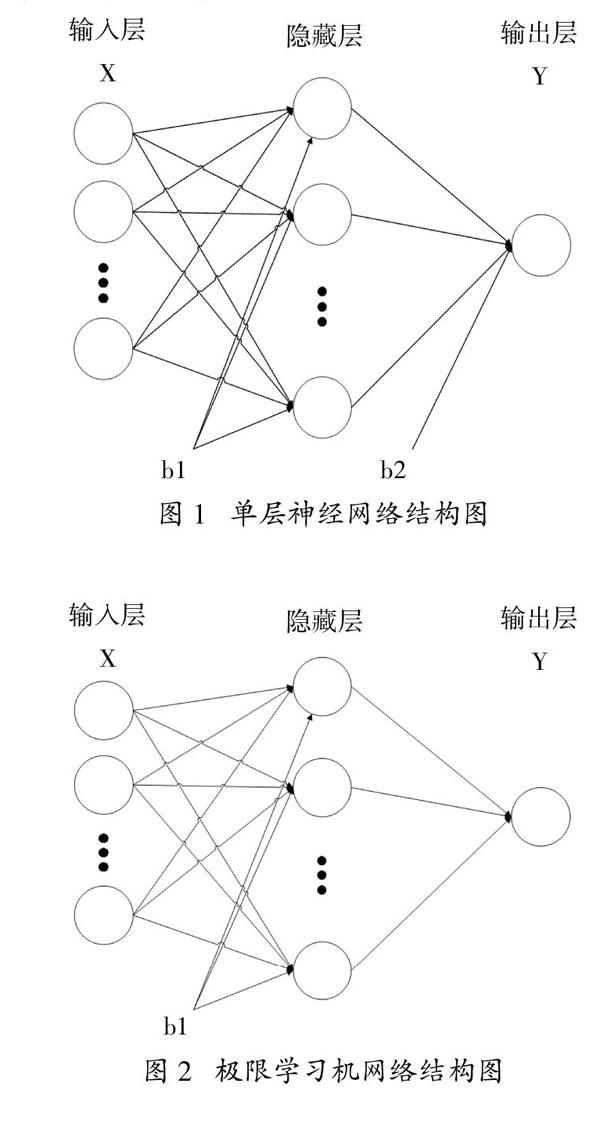
極限學習機[12-13]（Extreme Learning Machine，ELM）是Huang G B等人于2004年在前饋神經網絡基礎上提出的一種高效的機器學習算法。極限學習的結構和原理與單層神經網絡相似，如圖1和圖2，隱藏層把輸入層輸入向量映射至高維特征空間，輸出層為輸出權重矩陣，基于數據訓練學習各層權重參數。以擁有 個輸入層節點，個隱藏層節點，1個輸出層節點的 結構的單層反饋網絡為例，給定 個隨機樣本 輸出表示為

f（Xk） = ■βjg（Wj·Xk + b1j） + b2? k = 1，2，…，m

（1）

式中Wj = [wi1，wi2，…，wil]，i = 1，2，…，n，是隱藏層與輸入層的輸入權重向量，wij表示輸入層第 i個節點和隱藏層第j個節點之間的權值;βj是輸出層節點和隱藏層第j個節點的權值，bij是隱藏層第 j個節點激活函數的偏置量，b2是輸出層節點的偏置量，g（x）是如圖3的隱藏層激活函數Sigmoid。

單層神經網絡輸出表達式緊湊表示為

y = Hβ + b2，y∈R? ? ? ? （2）

圖1? ?單層神經網絡結構圖

圖2? ?極限學習機網絡結構圖

x

圖3? ?Sigmoid函數曲線圖

H =? [h1，h2，…，hl]是隱藏層輸出矩陣，hj = g（Wj·Xk + b1j），y是對應輸入矩陣的輸出層輸出。β =[β1，β2，…，βl]T是輸出層和隱藏層間的輸出權重向量網絡在第k個訓練樣本上的均方誤差為：

Ek = ■（yk - tk）2? ? ? ? （3）

單層神經網絡輸出表達式緊湊表示為

y = Hβ + b2，y∈R? ? ? ? （2）

H =? [h1，h2，…，hl]是隱藏層輸出矩陣，hj = g（Wj·Xk + b1j），y是對應輸入矩陣的輸出層輸出。β =[β1，β2，…，βl]T是輸出層和隱藏層間的輸出權重向量網絡在第k個訓練樣本上的均方誤差為：

Ek = ■（yk - tk）2? ? ? ? （3）

網絡中待確定的參數有：

1）輸入層到隱藏層的n × l個權值wij，

i = 1，2，…，n;j = 1，2，…，l;

2）隱藏層到輸出層的 個權值βj，j = 1，2，…，l;

3）隱層節點的l個閾值b1j，j = 1，2，…，l;

4）輸出層單節點的1個閾值b2。

目前廣泛使用BP算法求解這l × （ n + 2）個參數。BP核心在于鏈式求導法則的運用，基于梯度下降方法，以目標的負梯度方向對參數進行調整：

Δwij = -η■;Δβj = -η■;

Δb1j = -η■;Δb2 = -η■;

其中η是學習率。

可見單層反饋神經網絡參數復雜，且BP調參方法需要大量的微分和矩陣運算，致使整個模型訓練效率低。為解決該問題，極限學習機在此模型基礎上依據以下兩個理論提出。

理論1.1

給定一個N個隱藏層節點的標準單隱藏層反饋神經網絡（SLFN），且激勵函數η：R→R在任意區間無限可微，對于N個隨機不同樣本（xi，ti），{xi，ti|xi∈Rn，ti∈Rm}，以及依據任意連續概率分布在Rn和R空間任意區間隨機選擇的wi和bi，都有SLFN隱藏層輸出矩陣H可逆、 ‖Hβ-T‖概率1成立。

理論1.2

給定任意小正值ε<0，和在任意區間無限可微的激勵函數g：R→R，存在■≤N對于N個隨機不同樣本（xi，ti），{xi，ti|xi∈Rn，ti∈Rm}，以及依據任意連續概率分布在Rn和Rm空間任意區間隨機選擇的xi和 bi，都有‖HN × ■ β■ × m- TN × m‖<ε，概率1成立。

只要激勵函數滿足在任意區間無限可微，輸出層偏置就可以忽略不計，SLFN結構簡化如圖2。隱藏層權重矩陣wi、偏置矩陣bi可以在Rn 和R空間內依據任意連續概率分布隨機生成，不需要采用SLFN的鏈式求導法則，反向傳播進行調整。只要一次解析計算便求得輸出層權值矩陣β，如式4

其中，β是輸出層權重矩陣，T是輸出矩陣，H？覮是隱藏層輸出矩陣的Moore-Penrose廣義逆（偽逆），求解過程如式5

H？覮是矩陣H的左偽逆矩陣，帶入式4得β*式6最小二乘解計算方法

β* = （HTH）-1HTH? ? ? ?（6）

從而極大地減少了對計算資源的占用，降低了模型訓練時間。

訓練步驟如下：

1）由連續概率分布隨機設定隱藏層權重矩陣wi，偏置矩陣bi超參數;

2）計算隱藏層輸出矩陣h0;

3）根據式6計算輸出權重矩陣βk。

2? ?貝葉斯優化的ELM算法

極限學習機預隱藏層激勵函數通常選擇高斯徑向基函數，測模型的預測精度跟超參σ、隱藏層節點數n的設定密切相關。但超參數的調整是一個黑盒問題，無法解析求得。只能采用基于經驗的人工手動調節、近似窮舉的網格搜索，計算復雜較高的遺傳算法和粒子群算法等方法。上述方法雖能滿足模型訓練所需，但由于訓練時間較長，工程實踐中難運用。Martin Pelikan等人于1999年提出貝葉斯優化算法[14-15]（Bayesian Optimization Algorithm，BOA）。BOA算法是基于遺傳算法結合統計學理論的一種對目標分布的估計方法。貝葉斯優化相較于網格搜索，充分利用了歷史搜索點的信息，收斂速度更快;相較于智能優化算法具有更簡單的結構、更低的計算復雜度。其以高斯過程為先驗函數，采樣函數根據已有經驗數據，選擇新采樣點修正先驗函數。

優化步驟如下：

（1）定義目標函數：X* = argmax f（x）;

（2）隨機產生n個超參數初始樣本點，依據前人總結，超參數分布多服從高斯分布。高斯過程得出初始超參數的先驗分布;

（3）采樣函數（acquisition functions）基于期望增量expected-improvement最大化原則，選取使使得期望函數最大化的期望X;

（4）計算X的實際目標值 ，如果滿足條件要求，則輸出X作為最優超參數，否則將X及真實值 添入初始采樣點，重復（3）。

圖4是貝葉斯優化流程圖：

圖4? ?BOA流程圖

3? ?數值仿真

3.1? ?ELM算法測試

仿真實驗環境：操作系統Windows10，處理器Intel（R）Core（TM）i7-4710MQ CPU@2.50GHz，內存8GB，仿真軟件MATLAB2018a。算法可行性實驗4.1、4.2采用UCI的Concrete Compressive Strength數據，如表1. 包含1030條樣本，每個樣本有8個特征維度。應用實驗4.3樣本來源于實際施工中標號C50混凝土的拌合站數據，如表2. 有1135條樣本，每個樣本有9個特征維度。合并相同特征，并依據三倍方差原則剔除了異常數據。因同批次試塊抗壓強度的測量結果非定值而成正態分布，實驗中的強度數據是同批次三個試塊的均值，致使數據自身既存在一定范圍的誤差。在文獻2中預測相對誤差平均值7.33%，文獻7中預測相對誤差平均值5.04%，普遍在5%左右，且滿足工程需求。將5%相對誤差作為可行性的評判標準。

為驗證極限學習機的泛化性能和計算效率，進行如下極限學習機、BP神經網絡和支持向量機對比實驗。BP網絡為9-9-1結構，輸入層9個節點，隱藏層9個節點，輸出層1個節點，核函數為高斯函數。ELM采用相同結構。支持向量機選取高斯核。三種算法核參數均由網格搜索方法尋優獲得。訓練時間忽略超參尋優。混凝土數據分為800條用于模型訓練、230條用于驗證。實驗分別進行50次，平均結果如表3，圖5是其中某次的實驗結果。極限學習與支持向量機的訓練時間相近，短于BP神經網絡。實驗中BP神經網絡的預測精度最高，但由于BP神經網絡基于鏈式求導法則，誤差反向傳播方法迭代計算的特性，計算性能最差，訓練時間最長。

表3? ?ELM、SVM和BP對比實驗結果平均值

樣本編號

圖5? ?單次ELM、SVM和BP對比實驗結果

3.2? ?貝葉斯超參數優化

為驗證貝葉斯優化算法（BOA）的高效性，將其與常用的網格搜索（GS）、遺傳算法（GA）以及粒子群算法（PSO）優化的極限學習機進行對比實驗。參數尋優算法中，設置超參數搜索空間 ，該值由多次試驗經驗值基礎上獲得，并考慮到實際需求，避免意外情況略增大搜索范圍。GS搜索步長0.5，BO采樣函數使用expected-improvement-plus，GA、PSO步長（StepTolerance）設置0.5。相對誤差率、訓練時間以及尋優算法的迭代次數如表4。四種算法的泛化誤差雖然相近，在4%左右滿足實際需求，但貝葉斯優化算法以其極快的收斂速度較低的計算復雜度，迭代次數最少，訓練時間最短。表明了貝葉斯優化算法在該問題模型上超參尋優的高效性。

表4? ?BOA、GA、PSO和GS對比實驗結果平均值

3.3? ?BOA-ELM算法應用

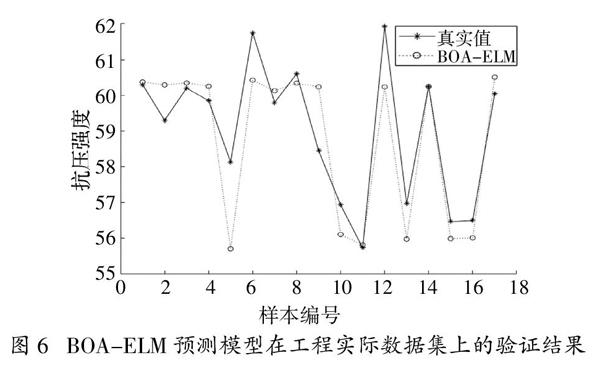
為驗證BOA-ELM算法在混凝土生產過程中的實際表現情況，采集C50混凝土拌合站數據和壓力機數據如表2。800條用于模型訓練，335條用于模型驗證。基于該數據集驗證BOA-ELM預測模型的現實性能。圖6是部分運行結果，訓練時間15.5110s，平均預測相對誤差2.0209%小于5%，優于期望，滿足實際需求。

樣本編號

圖6? ?BOA-ELM預測模型在工程實際數據集上的驗證結果

4? ?結 論

針對C50標號混凝土進行抗壓強度預測研究，根據施工現場對實時性有較高要求的特點，采用極限學習機高效建模方法。由于預測模型的泛化精度極大程度受超參數影響，為降低超參尋優的耗時，選擇貝葉斯優化方法對ELM進行超參調優。并在實際施工產生的C50數據集上進行了實驗仿真。實驗表明本文提出的方法相較于其他，能夠快速地訓練預測模型、較準確地預測出混凝土強度，適合混凝土抗壓強度預測的實際應用。

參考文獻

[1]? ? 靳江偉，董春芳，馮國紅. 基于灰色關聯支持向量機的混凝土抗壓強度預測[J]. 鄭州大學學報：理學版，2015（3）：59—63.

[2]? ? 汪瀾. 水泥混凝土：組成、性能和應用[M]. 北京：建材工業出版社，2005.

[3]? ? 李章建，宋楊會，李世華. 偏高嶺土高性能混凝土抗壓強度預測研究[J]. 硅酸鹽通報，2017，36（9）.

[4]? ? 范立強，呂國芳. 基于高維云RBF神經網絡的混凝土強度預測[J]. 電子設計工程，2016，24（08）：80—82.

[5]? ? KHADEMI F ， AKBARI M ， JAMAL S M ，et al. Multiple linear regression，artificial neural network，and fuzzy logic prediction of 28 days compressive strength of concrete[J].Frontiers of Structural and Civil Engineering，2017，11（1）：90—99.

[6]? ? 龔珍，卜小波，吳浩. 基于PSO-SVM的混凝土抗壓強度預測模型[J]. 混凝土，2013（12）：11—13.

[7]? ? 張靜，劉向東. 混沌粒子群算法優化最小二乘支持向量機的混凝土強度預測[J]. 吉林大學學報：工學版，2016，46（4）：1097—1102.

[8]? ? 嚴東，湯健，趙立杰. 基于特征提取和極限學習機的軟測量方法[J]. 控制工程，2013，20（1）：55—58.

[9]? ? XIAO T，REN D，LEI S ，et al. Based on grid-search and PSO parameter optimization for Support Vector Machine[C]. Intelligent Control & Automation. IEEE，2015.

[10]? ROBLES-RODRIGUEZ C E ，BIDEAUX C ，ROUX G ，et al. Soft-sensors for lipid fermentation variables based on PSO support vector machine （PSO-SVM）[M] Distributed Computing and Artificial Intelligence，13th International Conference. Springer International Publishing，2016.

[11]? 李剛，王貴龍，薛惠鋒. RVM核參數的遺傳算法優化方法[J]. 控制工程，2010，17（3）：335—337.

[12]? HUANG G B，ZHU Q Y，SIEW C K. Extreme learning machine：Theory and applications[J]. Neurocomputing，2006，70（1）：489—501.

[13]? HUANG G B，ZHOU H，DING X，et al. Extreme learning machine for regression and multiclass classification[J]. IEEE Trans Syst Man Cybern B Cybern，2012，42（2）：513—529.

[14]? SHAHRIARI B，SWERSKY K，WANG Z，et al. Taking the human out of the loop：a review of Bayesian optimization[J].Proceedings of the IEEE，2015，104（1）：148—175.

[15]? 江敏，陳一民. 貝葉斯優化算法的發展綜述[J].計算機工程與設計，2010，31（14）：3254—3259.