基于形態學重建改進的FCM算法

候慧　李水艷

摘? ?要：傳統的FCM（fuzzy c-means）算法可以準確的分割多數無噪聲圖像，但對噪聲圖像非常敏感。針對于此類問題，提出了一種基于形態學重建的改進FCM算法。首先利用形態學閉合重建算子對含噪圖像進行光滑化。然后利用基于鄰域信息的改進FCM算法對合成圖像及醫學圖像進行分割處理，最終得出了更加精確的分割結果。通過與其它兩類算法進行數值實驗對比，驗證了所提出算法的有效性和實用性。

關鍵詞：圖像分割;形態學重建;模糊c均值算法

中圖分類號：TP391.41? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?文獻標識碼：A

Improved FCM Algorithm Based on Morphological Reconstruction

HOU Hui？覮，LI Shui-yan

（College of Science，Hohai University，Nanjing，Jiangsu? 211100，China）

Abstract：The traditional fuzzy c-means（FCM） algorithm can segment noiseless images accurately，but it is very sensitive to noise. Aiming at such problems，an improved FCM algorithm based on morphological reconstruction is proposed. First，the morphological closing reconstruction operator is used to smooth the noisy image. Then，the improved FCM algorithm designed by the neighborhood information is used to segment the composite image and the medical image. Finally，we get more accurate segmentation results. The effectiveness and practicability of the proposed algorithm are verified by numerical experiments with other two types of algorithms.

Key words：image segmentation;morphological reconstruction;fuzzy c-means algorithm

近年來，圖像分割在圖像分析[1]、模式識別[2]、計算機視覺[3]等領域發揮了重要的作用。針對于圖像分割問題，國內外學者已經提出了眾多方法[4-7]。圖像分割技術大致可分為四類，即強度閾值技術[4]、基于邊緣的方法[5]、基于區域的方法[6]和基于聚類的方法[7]。由于噪聲的影響出現了邊界特征模糊、灰度不均勻等現象，因此在圖像分割中如何降低噪聲干擾，提高分割精度受到了眾多學者廣泛關注。

眾所周知，傳統的FCM算法能夠有效分割多數無噪聲圖像，然而對噪聲圖像非常敏感。為了解決該問題，學者們提出了一系列改進FCM相關算法[8-12]。Adhikari等人[8]將條件變量和局部信息合并到隸屬度函數中，對FCM算法進行了改進。該方法已成功地應用于核磁共振（MRI）腦圖像的分割上。Elazab等人[9]提出了一種FCM框架，該框架利用鄰域灰度的異質性來獲取局部上下文信息，并將高斯徑向基核函數引入目標函數中。最近，Gharieb等人[10]引入了一種改進的FCM算法，該算法基于局部隸屬度和局部平滑數據，結合Kullback-Leibler散度進行圖像分割。Gong等人[11]提出了一種基于核度量的FCM算法，該算法依賴于局部信息來評估像素鄰域的阻尼程度。Lei等人[12]利用隸屬度濾波修正隸屬度矩陣以避免大量的迭代計算，它在分割人工圖像和真實圖像方面獲得了成功的應用。

提出了一種基于形態學重建的改進FCM圖像分割算法。首先利用形態學閉合重建算子對圖像進行光滑化，解決了FCM算法對噪聲敏感的問題。然后，使用結合鄰域信息的改進FCM算法對含噪圖像進行分割。通過實驗的對比驗證了該算法具有較好的分割效果，同時取得了較高的分割精度。

1? ?傳統FCM算法

圖像可通過向量X = {x1，x1，…，xN}來表示，其中xi為第i個像素節點，N為總像素數。傳統FCM算法是一種基于劃分的聚類算法，主要思想是通過求解下列目標函數最小化問題進而將X劃分成 c類：

J（H，y） = ■■hmij‖xj - yi‖2

s.t.? ？坌j ∈ 1，2，…，N：■hij = 1，

？坌j∈1，2，…，N，？坌j∈1，2，…，c： hij∈0，1

（1）

其中，H = [hij]c×N為隸屬度矩陣，m為模糊系數（m>1），c為聚類個數，‖·‖代表歐式距離。隸屬度矩陣hij和類中心yi的迭代過程分別如下：

hij = ■? ? （2）

yj = ■? （3）

根據文獻[13]，我們假設當‖y（t）? - y（t-1） ‖<ε時停止迭代。其中ε > 0為迭代閾值，t為算法的迭代次數。

2? ?基于形態學重建的改進FCM算法

2.1? ?形態學重建（MR）

形態學重建能夠對帶有噪聲圖像起到降噪的作用，同時保留了重要的目標輪廓，這對進一步利用改進FCM算法對圖像進行分割起到了至關重要的作用。形態學重建算法包含兩個基本操作：膨脹和腐蝕[14]。

定義1：若f為標記圖像，g為模板圖像，B為結構元，并且f■g，則f關于g的大小為1的膨脹算子為：D（1）g（f） = （f ■ B）∩g;進而f關于g大小為n的膨脹算子為：D（n）g（f） = D（1）g（D（n-1）g（f）），其中D（0）g（f） = f。

定義2：若f為標記圖像，g為模板圖像，B為結構元，并且f■g，則f關于g大小為1的腐蝕為： E（1）g（f） = f ■ B）∪g，f關于g大小為 的腐蝕為：E（n）g（f） = E（1）g（E（n-1）g（f）），其中E（0）g（f） = f。

通過形態學膨脹算子和腐蝕算子進行組合，可以得出一些具有較強濾波能力的重建算子，如形態學開啟和閉合重建算子。由于形態學閉合重建算子更適合于平滑紋理細節，因此我們采用形態學閉合重建算子對噪聲圖像進行光滑化。圖像f大小為n的閉合重建算子為：

C（n）R（f） = REf（f ■nB）? ? ? ? ?（4）

式中，f ■nB表示B對f的n次膨脹。利用MR對圖像光滑化后的效果如圖1所示。

■

（a） 原圖像? ? ? ? ? ? ? ? ? ?（b）加噪圖像? ? ? ? ? ? ? （c）光滑后圖像

圖1? ?MR光滑化效果圖

2.2? ?結合鄰域信息的FCM算法

圖像f可由向量X = {x1，x1，…，xN}表示，經過MR光滑化后的圖像記為f = X = {x1，x1，…，xN}。借助于像素點的鄰域信息，我們可以得到改進FCM算法，該算法的目標函數定義如下：

J（H，y） = ■■hmij‖xj - yi‖2 + μ‖■j - yi‖2

s.t.? ? ? ∈1，2，…，N：■hij = 1，

∈1，2，…，N，Aj∈1，2，…，c：hij∈0，1

（5）

式中，μ為控制參數。

由（5）式可得到以下迭代解：

hij=■? （6）

yj = ■? ? ? ? ? ?（7）

同理，當‖y（t）? - y（t-1） ‖<ε時停止迭代。算法? ? ? ? 流程如圖2所示。

圖2? ?算法流程圖

3? ?數值實驗比較

在本節中，為驗證算法的有效性和實用性，算法在Matlab2018上進行編程，在Windows 8環境下調試。實驗圖像選取了合成圖像和醫學圖像。合成圖像為在原圖像上加入了均值為0，方差為0.02的高斯白噪聲。為了與其它算法進行更鮮明的對比，我們對合成圖像依次執行文獻[9]中ARKFCM算法，文獻[12]中FRFCM算法和本文算法進行對比實驗。算法參數分別設為c = 4，m = 2，ε =1 × 10-6。三種算法對合成圖像的分割效果如圖3所示。

在合成圖像的比較實驗中，從視覺效果上可以鮮明看出，本文提出的改進FCM算法比ARKFCM[9]和FRFCM[12]對含噪圖像的分割更準確。同時為了進一步驗證本文算法的優越性，我們利用性能指標對分割效果進行數值檢驗，本文采用的性能指標為分割精度SA[15]。SA的表達式定義如下：

SA = ■■? ?（8）

（a）原圖像? （b）噪音圖像? （c）ARKFCM? （d）FRFCM? （e）本文算法

圖3? ?三種算法對合成圖像的分割效果圖

將此性能指標應用與上述三種算法中，分別得出分割精度SA值見表1。

表1? ?不同算法的分割精確度值（SA）

由表1數據可知，本文提出的改進FCM算法的SA值基本高于其它兩類算法。基于上述分析，本文提出的算法在視覺和數值上均具有較強的優越性。因此，該算法具有一定的推廣價值。

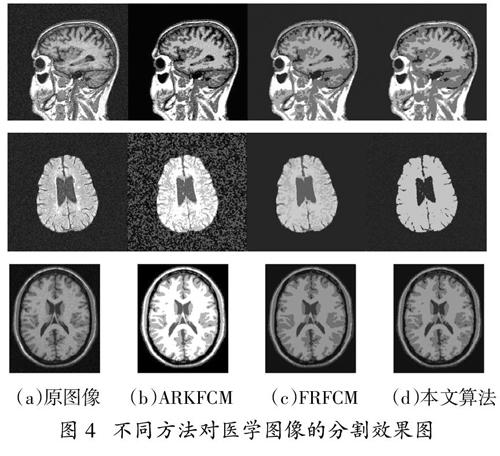
同理，對于醫學圖像我們也進行了相應的比較實驗，分割效果如圖4所示。

（a）原圖像? ? ? （b）ARKFCM? ? ? ? （c）FRFCM? ? ? ?（d）本文算法

圖4? ?不同方法對醫學圖像的分割效果圖

由圖4可以看出，ARKFCM算法的抗噪性較弱。FRFCM算法雖與本文算法分割效果較為一致，但在細節的分割上低于本文算法。

5? ?結? 論

提出了一種基于形態學閉合重建的改進FCM分割算法。通過引入形態學閉合重建算子，對噪音圖像進行光滑化，在抑制噪聲的同時保護圖像的細節特征。結合鄰域信息對FCM算法進行改進，提高了對噪聲圖像的分割精度。實驗結果表明該算法對合成圖像和醫學圖像提供了更好的分割結果，并且對噪聲的魯棒性方面有了很大的提升. 在實際應用中具有一定的推廣意義。

參考文獻

[1]? ? LITJENS G，KOOI T，BEJNORDI B E，et al. A survey on deep learning in medical image analysis[J]. Medical Image Analysis，2017，42：60—88.

[2]? ? WRIGHT J，MA Y，MAIRAL J，et al. Sparse representation for computer vision and pattern recognition[J]. Proceedings of the IEEE，2010，98（6）：1031—1044.

[3]? ? ATHANASIOS V，NIKOLAOS D，ANASTASIOS D，et al. Deep learning for computer vision：a brief review[J]. Computational Intelligence and Neuroscience，2018：1—13.

[4]? ? TAN K S，ISA N A M. Color image segmentation using histogram thresholding-fuzzy c-means hybrid approach[J]. Pattern Recognition，2011，44（1）：1—15.

[5]? ? PICHEL J C，SINGH D E，RIVERA F F. Image segmentation based on merging of sub-optimal segmentations[J]. Pattern Recognition Letters，2006，27（10）：1105—1116.

[6]? ? FAN J，YAU D K Y，ELMAGARMID A K，et al. Image segmentation by integrating color edge detection and seeded region growing[J]. IEEE Transactions on Image Processing，2001，10（10）：1454—1466.

[7]? ? ZHU X，PEDRYCZ W，LI Z. Fuzzy clustering with nonlinearly transformed data[J]. Applied Soft Computing，2017，61：364— 376.

[8]? ? ADHIKARI S K，SING J K，BASU D K，et al. Conditional spatial fuzzy c-means clustering algorithm for segmentation of MRI images[J]. Applied Soft Computing，2015，34：758—769.

[9]? ? ELAZAB A，WANG C，JIA F，et al. Segmentation of brain tissues from magnetic resonance images using adaptively regularized kernel-based fuzzy c-means clustering[J]. Computational and Mathematical Methods in Medicine，2015，5：1—12.

[10]? GHARIEB R R，GENDY G，ABDELFATTAH A，et al. Adaptive local data and membership based KL divergence incorporating c-means algorithm for fuzzy image segmentation[J]. Applied Soft Computing，2017，59：143—152.

[11]? GONG M，LIANG Y，SHI J. Fuzzy c-means clustering with local information and kernel metric for image segmentation[J]. IEEE Transactions on Image Processing，2012，22（2）：573—584.

[12]? LEI T，JIA X，ZHANG Y，et al. Significantly fast and robust fuzzy c-means clustering algorithm based on morphological reconstruction and membership filtering[J]. IEEE Transactions on Fuzzy Systems，2018，26（5）：3027—3041.

[13]? SOULEYMANE BALLAARABE S，GAO X，WANG B. A fast and robust level set method for image segmentation using fuzzy clustering and lattice Boltzmann method[J]. IEEE Transactions on Cybernetics，2013，43（3）：910—920.

[14]? PLISSITI M E，NIKOU C，CHARCHANTI A. Automated detection of cell nuclei in pap smear images using morphological reconstruction and clustering[J]. IEEE Transactions on Information Technology in Biomedicine：a Publication of the IEEE Engineering in Medicine and Biology Society，2011，15（2）：233—241.

[15]? MA J，TIAN D，GONG M，et al. Fuzzy clustering with non-local information for image segmentation[J]. International Journal of Machine Learning and Cybernetics，2014，5（6）：845—859.