基于網格對應的雙約束特征點匹配算法

林敏　陳姝　袁浩翔

摘? ?要：常用的特征點匹配算法通常設置嚴苛的閾值以剔除錯誤匹配，但這樣也會導致過多的正確匹配被刪除。針對這一問題，提出了一種采用雙約束的特征點匹配方法。首先，在局部上統計特征點匹配數量，運用網格對應的方法過濾部分錯誤匹配;然后，在全局上運用RANSAC方法計算基礎矩陣，通過極線約束對匹配進行再一次篩選。實驗表明，相比于傳統的匹配算法，該算法能在不增加算法運行時間的前提下，獲得更高數量和更高質量的匹配集合。

關鍵詞：特征點匹配;誤匹配;網格對應;RANSAC;極線約束

中圖分類號：TP391.4? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?文獻標識碼：A

Feature Point Matching Based on Double Constraints

LIN Min？覮，CHEN Shu，YUAN Hao-xiang

（College of Information Engineering，Xiangtan University，Xiangtan，Hunan 411105，China）

Abstract：Commonly used feature point matching algorithms usually set strict thresholds to eliminate false matches，which may cause many correct matches to be deleted. To overcome this problem，a feature matching algorithm using double constraints isproposed. Firstly，we statistically count the number of feature point matches in local to establish a grid correspondence，which can be used to filter out partial false matches. Then，the RANSAC was globally introduced to calculate the fundamental matrix，and the matching is once again filtered by the epipolar constraint. Experiments show that compared to the traditional matching algorithm，our algorithm can obtain a higher number and higher quality matching set without additional running time.

Key words：feature point matching;false matches;grid correspondence;RANSAC;epipolar constraint

圖像特征點匹配[1]旨在建立同一對象或場景不同視圖之間的精確對應關系，其結果一般作為高級計算機視覺算法應用的輸入，因此特征點匹配在三維重建[2]，目標跟蹤[3]，物體識別[4]，slam[5]等領域都起著至關重要的作用。

目前最常用的特征點匹配策略分為兩步。首先，用Flann[6]等匹配器通過比較特征描述子的相似性以刪除掉大部分錯誤匹配，確定基礎匹配集合。然后，對于匹配集合采用統計回歸[7]，RANSAC[8]等方法對匹配進行驗證，最終獲得魯棒的特征點匹配集合。Bay等人通過改變特征點檢測方式和降低特征描述維度等方法，提出了眾多抗干擾強，速度快的特征點匹配算法[9，10]，但仍是通過相似度來確認特征是否匹配。而Lowe等人對SIFT特征點[11]的研究表明最近鄰距離比值法（NNDR，Nearest Neighbor Distance Ratio）可以有效區分匹配是否正確，但是比率閾值難以設計，寬松的閾值會導致誤匹配數量激增，嚴苛的閾值往往將很多正確匹配也排除在外。Bian[12]等人提出采用運動平滑來約束匹配，用網格統計（GMS，grid-based motion statistics）的方法將高數量匹配轉換為高質量匹配，但算法需要提取數量巨大的特征點，且誤匹配容易“扎堆”出現。文獻[13]使用RANSAC方法通過極線約束來提高匹配精度，但算法復雜度高，十分耗時。文獻[14]和文獻[15]分別針對特征點匹配中難以解決的寬基線和重復結構問題分別提出Code和Repmatch方法，兩者都取得了很好的匹配效果，但因為算法復雜，運行較慢。

本算法主要針對特征點匹配進行研究。采用網格對應取代閾值設置對匹配進行首次粗過濾。然后采用RANSAC方法對匹配進行二次篩選。實驗證明，網格對應能保留更多的正確匹配，而經過兩次過濾后的匹配集合在匹配數量和匹配準確度上都有明顯提高。

1? ?雙約束原理與實現

1.1? ?相關原理

1.1.1? ?網格對應

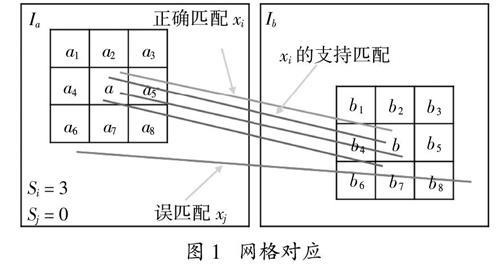
網格對應是根據運動相似性原理，通過統計匹配分布，將匹配約束在對應網格中來達到去除誤匹配的目的。

圖1? ?網格對應

在一般的網格對應中，圖像對{Ia，Ib}各有{N，M}個特征點，X = {x1，x2，…，xi，…，xN}是根據特征點描述子相似度得出的基礎匹配集合，取匹配x_i兩個特征點周圍的小區域{a，b}，它們分別對應有{n，m}個特征點，{a，b}內其它匹配滿足Xi■X。由此可以計算匹配xi的鄰域支持度Si：

Si = Xi - 1? ? ? （1）

如圖1所示，用網格對應近似表示匹配xi及其鄰域。與（1）類似，對應網格的鄰域支持度表示為：

Sab = ■x akbk? ? ? （2）

用pt和pf分別表示正確匹配和錯誤匹配的概率，則可以用一組二項式分布函數近似表示對應網格內正確匹配和錯誤匹配的鄰域支持度：

Si ～ B（Kn，pt），if xi is trueB（Kn，pf），if xi is false? ? ? （3）

由于正確匹配和錯誤匹配各自的鄰域支持度遵循不同的分布，所以Si整體上呈雙峰分布，這使得鄰域支持度Si可以成為區分網格是否正確對應的一個重要指標。

本文算法根據不同的特征點分布情況設置不同的鄰域支持度閾值來確立網格對應。當特征點分布稀疏時，意味著匹配分布也是稀疏的，此時網格鄰域支持度會很小，設置閾值τ′ = 2，剔除網格鄰域支持度小于2的對應網格。而針對特征點聚集區域，設置閾值τ′′ = ■，sum是9個網格內的匹配數，剔除網格鄰域支持度在9個網格內占比不足1/8的對應網格。由此得到的匹配都約束在一定條件下的對應網格內，雖然這樣的網格對應并不能完全將誤匹配去除，但這也為后續的極線約束奠定了良好的基礎。

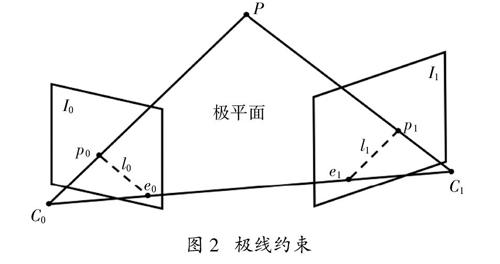
圖2? ?極線約束

1.1.2? ?極線約束

極線約束源于對極幾何[16]，它描述了兩幅視圖之間內在的射影關系。一幅視圖中的點定義了另一幅視圖中對應點所在的極線。圖2是極線約束的基本介紹。P是空間中一三維點，C0和C1表示相機中心，空間點在兩攝像機成像平面的投影分別為p0和p1，P和兩個相機中心構成的平面稱為極平面，點p0和p1均在此平面上。該平面和兩個成像平面的交線即為極線。點p0在第二幅視圖上的對應點必在極線l1上，同理p1點的對應點必在l0上。可以用基本矩陣F表示這種從點到直線的射影映射關系，即：

l = ABC = Fp = Fxy1? ? （4）

1.2? ?雙約束特征點匹配

基于網格對應的雙約束特征點匹配算法實現的具體步驟如下：

1）讀取待匹配的圖像對，經過暴力匹配和對稱性檢測獲得一個基礎的匹配集合。

2）采用網格對應的方法對匹配進行第一次篩

選。分兩種情況設置不同的網格對應閾值以確立網格對應，步驟如下：

a）將圖像對{Ia，Ib}各自劃分成G個網格;

b）圖像Ia的每個網格根據匹配數最大的原則

找Ib中對應網格;

c）計算對應網格的鄰域支持度Sab;

d）如果Sab大于τ′和τ′′中相對較大的那個，則認為網格對應;

e）剔除掉不滿足網格對應的匹配。

3）將網格對應后的匹配集合作為RANSAC算法的輸入，計算出具有最大匹配支持集合的基本矩陣F，并獲得第二次約束后的匹配集合。RANSAC算法采用迭代的方式自動估計F，步驟如下：

a）從匹配集合中隨機選取一個匹配子集Ti，假設Ti的所有匹配滿足極線約束;

b）由Ti內的匹配點對計算基本矩陣F;

c）用得到的F去測試其他其它所有匹配，將滿足約束的匹配歸入子集Ti中;

d）如果Ti內匹配數量足夠多，則認為計算出來的F足夠合理;

e）以上過程重復執行固定次數，比較每次Ti內匹配數量，找出Ti的最大集合;

f）用更新后的Ti重新計算F，而Ti集合內的匹配即為滿足極線約束的匹配。

至此，完成了利用網格對應獲得優質匹配的整個過程。

2? ?實驗結果分析

實驗采用Intel■CoreTM i5-8265U CPU @ 1.60GHz，8GB內存的計算機，在vs2017上采用OpenCV開源圖像庫作為實驗平臺，選取公開數據集[17][18]的圖像作為實驗數據。實驗中所有參數都采用圖像庫默認參數設置。

2.1? ?匹配結果對比

為了能驗證算法的有效性，采SIFT特征點作為匹配對象，對比本文算法和不同閾值設置下NNDR算法的匹配結果。如圖3所示，括號內給出了正確匹配數和匹配數，r表示比率閾值。實驗發現，當r設置為0.8時NNDR算法的匹配結果最優，但本文算法仍比它多了19對正確匹配，這說明本文算法在剔除誤匹配的同時將更多正確匹配保留了下來。同時，如圖4所示，選取6組復雜度不同的圖像，包含簡單和復雜個體對象以及室內、外場景。將NNDR閾值設置為0.8，表1列出了兩種方法得到的匹配數據。從表1可以看出，本文算法在6組圖像中都取得了更多的匹配數和更高的匹配精度，說明本文算法針對不同種類的圖像都能取得不錯的匹配效果。

（a）NNDR+RANSAC（106/106）r = 0.8

（b）本文方法（125/125）

圖3? ?比例閾值法匹配與本文算法匹配對比

圖4? ?部分實驗圖像

另外，將本文算法運用到包含重復結構圖像的匹配中。如表2所示，實驗統計了5組匹配數據，本文算法同樣做到了在匹配數量和匹配質量上都優于另外兩種算法。圖5是其中一組數據的匹配效果圖。圖5（a）是用最鄰近距離比值法（NNDR）過濾部分匹配后再采用RANSAC方法得到的匹配結果，從圖中可以看出，雖然經過RANSAC極線約束，但仍存在較多誤匹配。圖5（b）為GMS算法的匹配結果圖，可以看出GMS算法的誤匹配數雖然有所減少，但也存在誤匹配聚集出現的問題。圖5（c）是本文算法得到的匹配結果。相較GMS算法，由于本文算法在網格對應的基礎上增加了一次極線約束的幾何驗證，所以獲得了更高質量的匹配結果。

（a）NNDR+RANSAC（446/510）

（b）GMS（460/480）

（c）本文方法（472/475）

圖5? ?包含重復結構圖像的匹配結果

2.2? ?時間復雜度對比

在圖像特征點匹配算法評價標準中，算法耗時同樣是一項重要指標。故如表3所示，列出上述總共11組數據NNDR方法RANSAC用時和本文算法RANSAC用時。由于RANSAC算法隨機采樣的機制，每組數據運行5次，取平均運行時間。從表中可以看出，本文算法雖然增加了正確匹配數量，但并未增加算法運行時間，相比之下本文算法有幾組數據的運行時間甚至更短，這也說明本文算法的網格對應部分能有效地篩除錯誤匹配，減少了RANSAC算法迭代運行時間。

表3? ?時間復雜度對比

3? ?結? 論

特征點匹配技術在眾多高級計算機視覺應用領域都具有相當重要的意義。對比采用閾值設置方式進行匹配選擇的算法，針對其難以設置理想閾值保留足夠多正確匹配的問題，本文引入網格對應和極線約束來對基礎匹配集合進行兩次篩選，匹配實驗結果表明，經過局部和全局上的兩次誤匹配剔除，本算法實現了在不增加算法運行時間和減少誤匹配的同時，極大地提高了正確匹配數量。

參考文獻

[1]? ? 肖明，鮑永亮，顏仲新. 基于點特征的圖像配準方法綜述[J]. 兵工學報，2015，2.

[2]? ? AGARWAL S，SNAVELY N，SIMON I，et al. Building Rome in aday[C]//IEEE International Conference on Computer Vision， 2009.

[3]? ? CHEN S，LIANG L，LIANG W，et al. 3D pose tracking with multi-template warping and SIFT correspondences[J]. IEEE Transactions on Circuits and Systems for Video Technology，2015，26（99）：1—1.

[4]? ? GUO Y，SOHEL F，BENNAMOUN M，et al. A novel local surface feature for 3D object recognition under clutter and occlusion[J]. Information Sciences，2015，293：196—213.

[5]? ? MUR-ARTAL R，MONTIEL J M M，TARDOS J D. ORB-SLAM：a versatile and accurate monocular SLAM system[J]. IEEE Transactions on Robotics，2015，31（5）：1147—1163.

[6]? ? MUJA M，LOWE D. Flann-fast library for approximate nearest neighbors user manual[J]. Computer Science Department，University of British Columbia，Vancouver，BC，Canada，2009.

[7]? ? LIU Y，DEDOMINICIS L，WEI B，et al. Regularization based iterative point match weighting for accurate rigid transformation estimation[J]. IEEE Transactions on Visualization and Computer Graphics，2015，21（9）：1058—1071.

[8]? ? FISCHLER M A，BOLLES R C. Random sample consensus：a paradigm for model fitting with applications to image analysis and automated cartography[J]. Communications of the ACM，1981，24（6）：381—395.

[9]? ? BAY H，TUYTELAARS T，VAN GOOL L. Surf：Speeded up robust features[C]//European Conference on Computer Vision. Springer，Berlin，Heidelberg，2006：404—417.

[10]? RUBLEE E，RABAUD V，KONOLIGE K，et al. ORB： an efficient alternative to SIFT or SURF[C]//2011 International conference on computer vision. Ieee，2011： 2564—2571.

[11]? LOWE D G. Distinctive image features from scale-invariant keypoints[J]. International journal of computer vision，2004，60（2）： 91—110.

[12]? BIAN J W，LIN W Y，MATSUSHITA Y，et al. GMS：grid-based motion statistics for fast，ultra-robust feature correspondence[C]// Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2017：4181—4190.

[13]? 陳潔，高志強，密保秀，等. 引入極線約束的SURF特征匹配算法[J]. 中國圖象圖形學報，2018，21（8）：1048—1056.

[14]? LIN W Y，WANG F，CHENG M M，et al. CODE：coherence based decision boundaries for feature correspondence[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence，2017：1—1.

[15]? LIN W Y，LIU S，JIANG N，et al. RepMatch：robust feature matching and pose for reconstructing modern cities[C]// European Conference on Computer Vision. Springer，Cham，2016.

[16]? HARTLEY R，ZISSERMAN A. Multiple view geometry in computer vision[M]. Cambridge University Press，2003.

[17]? SHAO H，SVOBODA T，VAN GOOL L. Zubud-zurich buildings database for image based recognition[J]. Computer Vision Lab，Swiss Federal Institute of Technology，Switzerland，Tech. Rep，2003，260（20）：6—8.

[18]? JRGEN S，ENGELHARD N，ENDRES F，et al. A benchmark for the evaluation of RGB-D SLAM systems[C]//2012 IEEE/RSJ International Conference on Intelligent Robots and Systems. IEEE，2012.